Методична розробка практичного заняття з використання інноваційних методів навчання

Міністерство освіти і науки України

Донецький національний університет економіки і торгівлі

імені  Михайла Туган-Барановського

Краматорський КОЛЕДЖ

 

 

 

 

 

 

 

 

 

Методична розробка

практичного заняття

з дисципліни: Вища математика

Тема: «Розв’язання диференціальних рівнянь»

Спеціальність: 076 «Підприємництво, торгівля та біржова діяльність»

за ОПП  «Економіка підприємства»

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2019

                                

Методична розробка практичного заняття з дисципліни «Вища математика». Підготувала  викладач Краматорського коледжу Донецького національного університету економіки і торгівлі імені Михайла  Туган-Барановського  Кулешова Н.М.

 

11.11.2019р.

 

Викладено методику проведення практичного заняття із застосуванням інноваційних освітніх технологій, що сприяє активізації уваги і мислення студентів, виховує відповідальність і  навички колективної роботи з теми «Розв’язання  диференціальних рівнянь». 

 

 

Для викладачів вищої математики закладів вищої освіти.

 

 

 

Рецензенти:

 

Чернова Л.І. - голова регіонального методичного об’єднання  викладачів математики Краматорсько- Слов’янського регіону, спеціаліст  вищої кваліфікаційної категорії, викладач математики Відокремленого структурного підрозділу Національного авіаційного університету Слов’янського коледжу  Національного авіаційного університету.                                                  

 

Шовкопляс Г.О. - викладач математики   вищої кваліфікаційної категорії Краматорського коледжу технології та дизайну.

 

 

 

 

Розглянуто і  схвалено на засіданні циклової комісії загальноосвітніх, гуманітарних та природничо-наукових  дисциплін 

Протокол № 4 від  13.11.2019р.                                                                 

 

 

 

 

 

 

 

 

 

 

 

ЗМІСТ

 

Передмова…..………………………………………………………………………..... 4

1. Методика проведення практичного заняття за темою  «Застосування визначеного інтегралу»

•       1.1. План заняття……………………………………………………..…...………… 6
•       1.2. Зміст заняття..………...…………………………….………...………………... 7
•       1.3. Методичне обґрунтування проведення заняття……………………………... 8
•       2. Література….…………………………………………………………..……....... 10

3. Додатки
   1.        Завдання щодо проведення актуалізації опорних знань студентів (Додаток  А)………………………. ……….…………………………….. 11
   2.        Інструкційна карта (Додаток  Б)………………………. ……….……….. 14
   3.        Картка самоконтролю (Додаток  В)………..………..………..…………. 17
   4.        Бланк підсумкового контролю (Додаток  Г)……………………………. 18
   5.        Критерії  оцінки знань студентів  (Додаток  Д)....…………..…..……… 19

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Передмова

Аналіз стану викладання курсу «Вищої математики» показує, що результати навчання студентів,рівень їх розумової діяльності, пізнавальної активності, самостійності в значній мірі не відповідають вимогам часу. Знання з математики майбутніх економістів носять формальний характер, не  відповідають  потребам  спеціальних  дисциплін  і  загальному  рівневі  підготовки  сучасного  фахівця.  Однією  з  головних  причин  цих  недоліків  є  недосконалість  методичної  системи  навчання  вищої  математики  та  навчально-методичного  забезпечення у закладах вищої освіти. Цілий ряд умов, таких як мотивація, наочність, інтерес до предмету, а також формування прийомів розумової  діяльності, не можуть бути ефективно реалізовані лише традиційними формами та методами навчання. Потрібне поєднання традиційної методики з впровадженням в навчальний процес сучасних інноваційних технологій.

Математичні дисципліни, які вивчаються у вузах, визначають кількісні відношення і просторові форми об’єктів реального світу. Глибокі знання про ці відношення і форми дозволяють краще зрозуміти їх матеріальний зміст. Загальновизнано, що математика є найбільш трудомісткою навчальною дисципліною, що вимагає від студентів постійної, кропіткої і значної за обсягом самостійної роботи. Тому одним з головних завдань викладача вищої математики, є формування і розвиток навичок вивчення вищої математики, елементів культури навчання і мислення через використання інноваційних та інформаційних технологій навчання, які допоможуть студентам краще засвоїти необхідні компоненти програми навчання, дозволять розвивати пізнавальні інтереси студентів, їх активність у навчальній діяльності, а також забезпечать формування і розвиток комунікативних якостей студентів.

        Дуже важливе для викладача завдання – навчити самостійно отримувати знання, а цього можна досягти шляхом схильності студента до творчого сприйняття навчального матеріалу і його бажання самостійно подолати труднощі, що виникають. Цьому значною мірою сприяють різні види і форми аудиторної роботи, нестандартні прийоми навчання, інтерактивні форми роботи на заняттях. Великі можливості представляє самостійна робота під час розв’язання задач і вправ на заняттях. Викладач має орієнтуватися на всіх студентів групи, маючи на увазі загальні знання в цілому і кожного студента окремо. Такий підхід спонукає до роботи і сильного студента, і слабого.

Практичне заняття з вищої математики з елементами тренінгових технологій на основі електронних ресурсів за темою «Розв’язання  диференціальних рівнянь» проводиться зі студентами спеціальності 076 «Підприємництво, торгівля та біржова діяльність» за ОПП  «Економіка підприємства» Метою заняття є формування практичних вмінь використання визначеного інтегралу при розв’язанні економічних задач та навичок застосування прикладних програм до розрахунків.

При проведенні заняття використовуються тренінгові технології: вправи, розроблені за допомогою LearningApps.org - сервісу для підтримки процесів навчання та викладання за допомогою невеликих модулів, інтерактивний метод опитування «Мікрофон», методика спільної одноразової роботи групи  «Мозковий штурм», техніка роботи в малих групах «Ажурна пилка».

Обрана форма проведення заняття  дає можливість викладачеві визначити рівень засвоєння теоретичного матеріалу з теми «Інтегральне числення та диференціальні рівняння», виявити недоліки в умінні застосовувати методи розв’язання диференціальних рівнянь, сформувати навички використовувати знання з інших дисциплін на заняттях з вищої математики і навпаки. Використання тренінгових технологій  забезпечують високу мотивацію, якість знань, активну життєву позицію. З метою інтенсифікації проведення заняття, раціонального використання часу, забезпечення наочності, для активізації розумової діяльності студентів передбачено використання систем комп’ютерної математики.

Методична розробка може бути використана викладачами математики закладів вищої освіти з метою підвищення якості проведення занять.  

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1. МЕТОДИКА ПРОВЕДЕННЯ ПРАКТИЧНОГО ЗАНЯТТЯ

 

1.        План заняття

Дисципліна:   Вища математика.

Тема заняття: «Розв’язання  диференціальних рівнянь».

Тип заняття: Формування практичних вмінь та навичок.

Вид заняття:   практичне. 

Форма проведення: з використанням тренінгових технологій та електронних ресурсів.

Група:   ЕП-17-А.

Дата проведення:   11.12.2019р.

Мета заняття:

методична:  удосконалити методику проведення практичного заняття з використанням  інноваційних освітніх технологій;

дидактична: формування практичних вмінь використання диференціальних рівнянь при розв’язанні економічних задач та навичок застосування прикладних програм до розрахунків;

виховна: формувати культуру математичної мови та пізнавального інтересу; розвиток інтелектуальних та творчих здібностей студентів.

 

Методичне забезпечення заняття: інструкційна карта (Додаток Б), картка самоконтролю (Додаток Б),   бланк підсумкового контролю (Додаток В), критерії  оцінки знань студентів (Додаток Г).

Технічні засоби навчання: персональний комп’ютер.

Міждисциплінарні зв'язки:

1.     Дисципліна: Математика.

  Теми: Похідна функції. Невизначений інтеграл. Визначений інтеграл.

2.     Дисципліна: Інформатика та комп’ютерна техніка .

  Теми: Програмне забезпечення ПК. Глобальна мережа Інтернет.

3.     Дисципліна: Економіка підприємства

 Теми: Товарні запаси підприємства. Нормалізація товарних запасів. Прибуток підприємства.

4.     Дисципліна:   Бухгалтерський облік.

  Тема: Облік доходів та витрат.

Внутрідисциплінарні зв’язки:

Дисципліна: Вища математика.

Теми: Похідна функції. Невизначений інтеграл. Визначений інтеграл.

 

1.2. Зміст заняття

1.  Організаційний момент:

1.       Привітання студентів
2.       Перевірка наявності студентів в аудиторії.
3.       Перевірка готовності студентів до проведення заняття.

 

2. Повідомлення теми, навчальних цілей заняття:

Тема: «Розв’язання  диференціальних рівнянь».

 Мета проведення заняття формування практичних вмінь використання диференціальних рівнянь при розв’язанні економічних задач та навичок застосування прикладних програм до розрахунків.

3. Мотивація навчальної (пізнавальної) діяльності студентів.

За допомогою диференціальних рівнянь досліджуються процеси і явища в природничих, соціальних і економічних науках.

Одним з головних завдань підприємств торгівлі та закладів ресторанного господарства є дослідження динаміки показників економічної діяльності. Використання диференціальних рівнянь при розв’язанні  задач прикладного характеру щодо визначення таких економічних показників як попит та пропозиція дає можливість обстежувати ці нерівномірно мінливі  показники і отримувати точні результати.

 

4. Підготовчий етап.

Актуалізація опорних знань проводиться методом розв’язання інтерактивної вправи на знаходження відповідності (Додаток А).

5. Основний етап проведення заняття

Заняття проводиться з використанням інструкційної карти (додаток Б).

6. Заключний етап:

        5.1. Підведення підсумків заняття.

        5.2. Оцінювання діяльності студентів на занятті.

7. Домашнє завдання. Виконати інтерактивні вправи  у додатку learningapps.org з папки «Домашня робота»:

 

7.1. Розмісти у групи хибні висловлювання та істинні висловлювання;

7.2. Вказати відповідність;

7.3. Знайти пару.

 

 

 

 

 

 

Методичне обґрунтування проведення заняття

Практичне заняття за темою «Розв’язання  диференціальних рівнянь» проводиться зі студентами спеціальності 076 «Підприємництво, торгівля та біржова діяльність» за ОПП  «Економіка підприємства»

Мета проведення заняття – формування практичних вмінь використання диференціальних рівнянь при розв’язанні економічних задач та навичок застосування прикладних програм до розрахунків.

Заняття починається з організаційного  моменту, який складається з привітання студентів та  перевірки наявності студентів в аудиторії.

При проведенні мотивації звертається увага на те, що за допомогою диференціальних рівнянь досліджуються процеси і явища в природних, соціальних і економічних науках. Одним з головних завдань підприємств торгівлі та закладів ресторанного господарства є дослідження динаміки показників економічної діяльності. Використання диференціальних рівнянь при розв’язанні  задач прикладного характеру щодо визначення таких економічних показників як попит та пропозиція дає можливість обстежувати ці нерівномірно мінливі  показники і отримувати точні результати.

На підготовчому етапі проводиться актуалізація опорних знань  студентів за допомогою математичного диктанту (Додаток А), створеного за допомогою on-line платформи learningapps.org.  Це дозволяє перевірити теоретичні знання з теми, готовність студентів до практичного заняття, а також сприяє активізації розумової діяльності. Студенти самостійно оцінюють виконане завдання (Максаимально 10 балів) і результати заносять в картку самоконтролю (Додаток В).

Безпосередньо практична робота виконується згідно з інструкційною картою (Додаток Б). Перед виконанням практичних завдань студенти ознайомлюються з організацією проведення заняття.

Основний етап передбачає виконання чотирьох видів завдань:

1) усне розв’язання найпростіших диференціальних рівнянь методом «Мікрофон»;

2) розв’язання диференціальних рівнянь в малих групах;

3)розв’язання задачі методом «мозкового штурму»;

4)розв’язання задач прикладного характеру за допомогою диференціальних рівнянь з використанням технології «Ажурна пилка»  за допомогою системи комп’ютерної математики SMath Studio.

Для усного розв’язання підібрані нескладні диференціальні рівняння з розподіленими змінними. Застосовується метод «Мікрофон», що надає можливість кожному відповісти швидко, по черзі, відповідаючи на запитання. Кожна відповідь оцінюється в 0,5 бали.

 Друге завдання  складається з диференціальних рівнянь першого порядку: з відокремлюваними змінними, однорідного та лінійного. Кожна група розв’язує своє завдання. Результат висвітлюється на дошці.

Третє завдання передбачає розв’язання прикладної задачі. Перед використанням технології «Ажурна пилка», з метою наведення алгоритму міркувань, викладач пропонує студентам групи розв’язати методом «мозкового штурму» економічну задачу за допомогою диференціальних рівнянь з метою активізації розумової діяльності, викладач пропонує студентам навідні питання:

1. Який порядок даного рівняння?
2. Якого типу дане рівняння?
3. За допомогою якої формули розв’язується дане рівняння?
4. Як називається задача знаходження часткового розв’язку?
5. Які початкові умови задачі?
6. Який алгоритм розв’язання даної задачі?

Після того як студенти відповіли на питання, сформувалась технологія розв’язання задачі. До дошки викликається студент, який наводить рішення задачі.

Для роботи в малих групах застосовується «ажурна пилка» - це техніка групової роботи, яка допомагає активізувати всіх учасників. Викладач об’єднує учасників y команди, роздає поділений на частини навчальний матеріал. Кожна команда отримує одну частину завдання. Кожен учасник спочатку самостійно ознайомлюється з текстом завдання. Потім група спільно розв’язує завдання.  Після цього учасники переходять до нових команд (експертних команд), кожна з яких складатиметься з одного представника першого складу команд. Експерти розповідають про те, чого вони навчились y своїх попередніх командах. Розв’язки завдань (результати роботи в обох групах) перевіряються за допомогою системи комп’ютерної математики SMath Studio  самостійно. На завершення з метою перевірки рівня засвоєння матеріалу, пропонується невелика самостійна робота- розв’язання однієї з економічних задач.

Всі види робіт оцінюються як студентом так і викладачем. Наприкінці підводяться підсумки, оцінюється робота студентів, задається домашнє завдання. Оцінки виставляються у картку самоконтролю студентами (Додаток В) та в бланк підсумкового контролю знань, умінь, навичок викладачем (Додаток Г). В результаті розрахунків в електронній таблиці Excel, в кінці заняття студенти отримують оцінку самоконтролю та оцінку викладача за критеріями оцінки (Додаток Д).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ЛІТЕРАТУРА

Основна

1.  Дубовик В.П., Юрик І.І. Вища математика: Навч. посібник. – К.: А.С.К., 2009.

2. Литвин І.І. Вища математика: Навч. посібник. – К.: ЦНУ, 2009.

 

 

Додаткова

1.   Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2-х ч.: Учебное пособие для вузов. – М.: Высшая школа, 2000.
2.   Овчинников П.П. та ін. Вища математика: Підручник. У 2 ч. – К.: Техніка, 2004.
3.   Шипачёв В.С. Высшая математика: Учебник для вузов. – М.: Высшая школа, 1998.
4.   Шкіль М.І., Колесник Т.В. Вища математика. У 3-х кн.. – К: Либідь, 2004.
5.   Вища математика:  Збірник задач: Навч. посібник / За ред.  В.П. Дубовика, І.І. Юрика. – К.: А.С.К., 2004.
6.   Шипачёв В.С. Задачник по высшей математике: Учебное пособие для вузов.- М.: Высшая школа, 2002.

 

Інформаційні ресурси

1.               http://6201.org.ua/load/28
2.               http://mathsciences.at.ua/index/0-18
3.               http://www.allmath.ru/highermath.htm
4.               http://matem.com.ua/
5.               http://uk.wikipedia.org/wiki/Вища_математика
6.               http://www.scienceforum.ru/2014/444/440
7.               http://irbis.amursu.ru/DigitalLibrary/AmurSU _Edition/335.pdf

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Додаток А

Завдання щодо проведення актуалізації опорних знань студентів

Відкрити додаток learningapps.org та виконати наступне завдання:

 

Заповнити пропуски:

 

1)  називають вираз F(x,y,y',y'',…,y(n)) = 0, де x – незалежна змінна, y - невідома функція, y',y'',…,y(n) – похідні невідомої функції.
2) Розв´язком диференціального рівняння називають будь-яку , яка при підстановці її в рівняння перетворює його в тотожність.
3) Порядком диференціального рівняння називають, яка входить в це рівняння.
4) Загальним розв´язком диференціального рівняння називають таку , яка перетворює дане рівняння в тотожність і містить стільки незалежних довільних сталих, який порядок цього рівняння.
5) Процес знаходження загального розв´язку називають   диференціального рівняння.
6) Геометрично, загальному розв´язку диференціального рівняння відповідає сімейство всіх .
7)  називають значення функції та її похідних в заданій точці х0.
8) Розв´язок диференціального рівняння, який задовольняє заданим початковим умовам називають , а задачу знаходження часткового розв´язку – задачею Коші.
9) Диференціальні рівняння першого порядку– це рівняння, до яких входять похідні або диференціали не вище ніж  порядку. Диференціальне рівняння першого порядку може бути записане в неявному виді F(x,y,y’)=0, або розв’язане відносно похідної y’ =f(x,y).
10) Диференціальні рівняння з відокремлюваними змінними – рівняння виду  .                             

 

Відповіді:

1. Диференціальним  рівнянням  n - го порядку
2. Функцію
3. порядок найстаршої похідної
4. функцію
5. інтегруванням
6. інтегральних кривих
7. Початковими умовами
8. частковим розв´язком
9. першого
10. dy/dx=f(x)g(y)

 

Додаток Б

ІНСТРУКЦІЙНА КАРТА

ДО ПРОВЕДЕННЯ ПРАКТИЧНОГО ЗАНЯТТЯ №21

 

з дисципліни «Вища математика»

 

1. Тема: Інтегральне числення та диференціальні рівняння

2. Тема практичного заняття:  «Розв’язання  диференціальних рівнянь».

3. Мета проведення заняття: формувати практичні вміння та навички застосування визначеного інтегралу при розв’язанні прикладних задач, показати можливості застосування прикладних програм до розрахунку визначеного інтегралу             

3.1. Після виконаної роботи студент повинен:

знати: 

вміти: застосовувати властивості та таблицю інтегралів при розв’язанні диференціальних рівнянь, визначати вид диференціального рівняння, розв’язувати диференціальні рівняння першого порядку різного виду; використовувати диференціальні рівняння до обчислення економічних показників.

4. Матеріально-технічне оснащення : персональні комп’ютери, інструкційні карти, інтелектуальні карти, системи комп’ютерної математики.

5. Методичні вказівки

 Диференціальне рівняння -

                                                 Порядок диференціального рівняння - порядок найстаршої похідної

            Загальний розв'язок - функція від х, що залежить від (n- порядок рівняння), і задовольняє заданому диференціальному рівнянню.

              Частковий розв'язок - загальний розв'язок з фіксованим значенням.

                  Задача Коші - диференціальне рівняння + початкові умови.

   Розв'язок задачі Коші - знаходження часткового розв'язку при заданих початкових умовах.

 

Диференціальні рівняння першого порядку
Найпростіші	З відокремлюваними змінними	Лінійні	Однорідні ДР першого порядку
Привести до виду Проінтегрувати. Знайти загальний розв'язок. Знайти частковий розв'язок.	Розділити змінні   Проінтегрувати.   Знайти загальний розв'язок.   Знайти частковий розв'язок.	Заміна Одержали рівняння Вимагаєм       Знайшли Знаходимо u; Записати загальний розв'язок Знайти частковий розв'язок	Заміна Одержали рівняння відносно змінних x,z. Знайти z; Виконати обратну підстановку. Записати загальний розв'язок ДР Знайти частковий розв'язок

 

6. Зміст і послідовність виконання завдань

Завдання 1. Розв’язати рівняння

	y’ = х+3

Завдання 2. Знайти частинний розв’язок диференціального рівняння:

1) з початковою умовою

2)

3)

Завдання 3.

1.               Швидкість зростання кількості населення пропорційна кількості населення. Знайти закон зростання населення держави, в якій у 2019р. було 30 млн. населення. Яка кількість населення буде у 2020 р.?
2.               Попит і пропозиція – економічній категорії товарного виробництва.

Попит – представлена на ринку потреба в товарах, пропозиція – продукт, який є на ринку чи може бути доставлений на нього.

Нехай попит і пропозиція на товар визначаються відповідно співвідношеннями

  

де  – ціна товару; - тенденція формування ціни (похідна ціни за часом). Нехай також в початковий момент часу ціна р за одиницю товару складала 1 грош. од. Виходячи  з вимоги відповідності попиту пропозиції, знайти закон зміни ціни в залежності від часу.

3.               Швидкість обезцінювання обладнання внаслідок його зносу пропорційна в кожний даний момент часу його фактичній вартості. Початкова вартість – 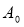 . Яка буде вартість обладнання після його використання впродовж t років?

Завдання 4. Самостійна робота. Розв’язати задачі самостійно та перевірити результати за допомогою системи комп’ютерної математики SMath Studio .

Варіант 1

1.Розв’язати диференціальне рівняння з відокремлюваними змінними:     .      

2. Знайти загальний розв’язок лінійного диференціального рівняння:

Варіант 2

1.Розв’язати диференціальні рівняння з відокремлюваними змінними:

            а)    ;          б) .

2. Знайти загальний розв’язок  однорідного  диференціального рівняння:

        .

Варіант 3.

1.Розв’язати диференціальне рівняння з відокремлюваними змінними:

2.Знайти загальний розв’язок лінійного диференціального рівняння:

 

7. Рекомендована література

Литвин І.І. Вища математика: Навч. посібник. – К.: ЦНУ, 2009., ст.  174-185

Додаток В

 

Картка самоконтролю

Група _______

 

Прізвище, ім’я, по батькові ______________________________________________.

 

№	Елементи практичного заняття	Максимальна кількість балів	Максимальна оцінка
	Актуалізація опорних знань
	Завдання на знаходження відповідностей. Теоретичні питання.	10
	Практична робота
	Завдання 1.	5
	Завдання 2.	5
	Завдання 3.	5
	Завдання 4.	5
	Завдання 5. Самостійна робота	5

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Додаток Г

Бланк підсумкового контролю знань, умінь,навичок

Дисципліна         Вища математика

Тема заняття       Розв’язання диференціальних рівнянь

Спеціальність     076«Підприємництво, торгівля та біржова діяльність»

за ОПП  «Економіка підприємства»

Група                  ЕП-17-А    курс ІІІ               

№	Прізвище, ім’я	Актуалізація опорних знань	Практична робота						Разом
			Розв’язання задачі методом «Ажурна пилка»					Самостійна робота
			№ 1	№ 2	№ 3	№4
		0,5 б	0,5 б	1б	1б	1б		1б
1	Бутенко Юлія
2	Запорожець Юлія
3	Кучер Олексій
4	Люшнева Каріна
5	Полторацька Анастасія
6	Сисукіна Альбіна
7	Сорокін Кирило
8	Треус Анастасія
9	Філатова Валерія
10	Фоменко Аліна

                            

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Додаток Д

Критерії оцінки знань студентів.

При виставленні оцінки   враховується:

•      правильність відповідей на теоретичні питання;
•      участь студентів в розв’язанні практичних завдань;
•      вміння володіти математичною термінологією;
•      вміння застосовувати теоретичні знання до розв’язання практичних задач.

На занятті використовується самооцінка студентів та оцінка викладача.

З метою прискорення оцінювання використовуються електронні таблиці Excel, за допомогою яких студенти самостійно виставляють отримані бали. Оцінка за практичне заняття обчислюється за допомогою формул на основі отриманих балів за кожне завдання.

 

Оцінка=(кількість балів студента)/(максимальна кількість балів за завдання)*(максимальна оцінка за завдання)

Максимальна кількість балів та відповідна максимальна оцінка за кожне завдання наведене в таблиці.

Таблиця 3. Максимальна кількість балів та відповідна максимальна оцінка завдань

№	Елементи практичного заняття	Максимальна кількість балів	Максимальна оцінка
	Актуалізація опорних знань.
	Завдання на знаходження відповідностей. Теоретичні питання.	10	0,5
	Практична робота
	Завдання 1. Знайти розв’язок диференціального рівняння першого порядку з розподіленими змінними.	5	0,5
	Завдання 2. Знайти розв’язок диференціального рівняння першого порядку.	5	1
	Завдання 3. Знайти розв’язок економічної задачі за допомогою диференціального рівняння.	5	1
	Завдання 4. Знайти розв’язок економічної задачі за допомогою диференціального рівняння.	5	1
	Самостійна робота	5	1

 

При виставленні кількості отриманих балів студентам рекомендовано враховувати наступний розподіл балів

 

 Талиця 4. Кількість балів за видами завдань та дій студента

№	Назва завдання	кількість балів
	Завдання на знаходження відповідностей: за кожну правильну відповідь	1
	Завдання 1-4.	5
2.1.	Вірно застосована формула	1
2.2.	Вірно застосований алгоритм розв’язання	1
2.3.	Вірно знайдене числове значення	1
2.4.	Введена формула в SMath Studio	1
2.5.	Результат перевірено програмою SMath Studio	1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Завдання 2.

1. Знайти частинний розв’язок диференціального рівняння

з початковою умовою

Розв’язання.

Запишемо рівняння в диференціалах:

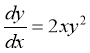
Відокремимо змінні:

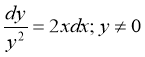
Проінтегруємо обидві частини рівності:

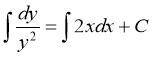
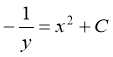
- загальний розв’язок диференціального рівняння.

Знайдемо частинний розв’язок диференціального рівняння. Для цього підставимо початкову умову в загальний розв’язок диференціального рівняння при , щоб отримати значення С. Отримаємо: . Звідси . Тоді .

Отже, частинний розв’язок диференціального рівняння має вигляд (рис.3):

 

 

 

 

Завдання 3

 

1. Попит і пропозиція – економічній категорії товарного виробництва. Попит – представлена на ринку потреба в товарах, пропозиція – продукт, який є на ринку чи може бути доставлений на нього.

Нехай попит і пропозиція на товар визначаються відповідно співвідношеннями

  

де  – ціна товару; - тенденція формування ціни (похідна ціни за часом). Нехай також в початковий момент часу ціна р за одиницю товару складала 1 грош. од. Виходячи  з вимоги відповідності попиту пропозиції, знайти закон зміни ціни в залежності від часу.

Розв’язання. Для того, щоб попит відповідав пропозиції, необхідно виконання рівності

Звідси

Маємо диференціальне рівняння з відокремлюваними змінними:

Врахуємо, що , тоді

   

Отже, щоб між попитом і пропозицією зберігалася рівновага, необхідно, щоб ціна змінювалася відповідно до отриманої формули.

 

2. Швидкість знецінення обладнання внаслідок його зносу пропорційна в кожний даний момент часу його фактичній вартості. Початкова вартість – 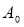 . Яка буде вартість обладнання після його використання впродовж t років?

Розв’язання. Нехай - вартість обладнання в момент t. Зміна вартості (обезцінювання) виражається різницею пропорційна фактичній вартості в даний момент . Одержуємо рівняння.

з початковою умовою

 Розв’язавши його, отримаємо:

     

        

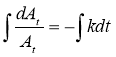
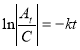
Для визначення довільної сталої С використаємо початкову умову при  t = 0:                                                         . Отриманий частинний розв’язок дає відповідь на питання даної задачі.

 

 

 

http://difur.in.ua/studentam/tests/

   -сайт с тестами по ДР

 

 

 

 

 

 

Нехай протягом деякого, достатньо тривалого часу підприємство продає на ринку власну продукцію. Причому виводить її на ринок лише один раз в тиждень. Тоді при наявних запасах продукції об’єм чергової партії буде залежати як від поточної ціни товару, так і від передбачуваної зміни ціни в подальшому. Якщо передбачається, що ціна в подальшому виросте, то пропозиція буде стримуватися за умови перекриття очікуваним подорожчанням витрат зберігання виготовленого уже товару. При цьому пропозиція товару в найближчий тиждень буде тим меншою, чим більшим передбачається подорожчання. І навпаки, якщо в подальшому очікується здешевлення продукції, то чергова пропозиція товару зросте тим більше, чим більшим передбачається зниження ціни в подальшому. Якщо позначити через p актуальну ціну продукції, а через p – так звану тенденцію формування ціни (похідну ціни часу), то як попит, так і пропозиція будуть функціями даних величин. При цьому, як показує практика, в залежності від різних факторів попит та пропозиція можуть бути різними функціями ціни p та тенденції формування ціни p . Дуже часто цю залежність можна вважати лінійною.

 

 

 

 

 

Попит та пропозиція – економічні категорії товарного виробництва, що виникають і функціонують на ринку, у сфері товарного обміну. При цьому попит – це представлена на ринку потреба в товарах, а пропозиція – це продукт, який є на ринку або може бути доставлений на нього. Одним з економічних законів товарного виробництва є закон попиту та пропозиції, який полягає в єдності попиту та пропозиції і їх об'єктивному прагненні до рівності. Розглянемо таку задачу. Нехай протягом деякого, достатньо тривалого часу підприємство продає на ринку власну продукцію. Причому виводить її на ринок лише один раз в тиждень. Тоді при наявних запасах продукції об’єм чергової партії буде залежати як від поточної ціни товару, так і від передбачуваної зміни ціни в подальшому. Якщо передбачається, що ціна в подальшому виросте, то пропозиція буде стримуватися за умови перекриття очікуваним подорожчанням витрат зберігання виготовленого уже товару. При цьому пропозиція товару в найближчий тиждень буде тим меншою, чим більшим передбачається подорожчання. І навпаки, якщо в подальшому очікується здешевлення продукції, то чергова пропозиція товару зросте тим більше, чим більшим передбачається зниження ціни в подальшому. Якщо позначити через p актуальну ціну продукції, а через p – так звану тенденцію формування ціни (похідну ціни часу), то як попит, так і пропозиція будуть функціями даних величин. При цьому, як показує практика, в залежності від різних факторів попит та пропозиція можуть бути різними функціями ціни p та тенденції формування ціни p . Дуже часто цю залежність можна вважати лінійною.

 

 

 

 

Теоретині питання.

 

Яке диференціальне рівняння називається звичайним? 2. Що називається диференціальним рівнянням першого порядку? 3. Що називається розв’язком диференціального рівняння? 4. Дати означення загального та частинного розв’язків диференціального рівняння першого порядку. 5. Сформулювати теорему Коші про існування та єдність розв’язку рівняння першого порядку. 26 6. Дати означення рівняння з відокремлюваними змінними. Як воно розв’язується? 7. Дати означення лінійного рівняння першого порядку та викласти метод його інтегрування. 8. Навести рівняння, звідні до лінійних та викласти методи їх інтегрування. 9. Дати означення рівняння Бернуллі. Як воно розв’язується?

 

 

 

 

 

 

 

Знайти відповідності.

 

 

Диференціальні рівняння закону попиту і пропозиції в економічних дослідженнях

Попит і пропозиція – економічні категорії товарного виробництва. Попит – представлена на ринку потреба в товарах, пропозиція – продукт, який є на ринку чи може бути доставлений на нього.

Нехай – ціна, наприклад, на фрукти, – тенденція формування ціни. Тоді, як попит так і пропозиція будуть функціями введених величин. Як показує практика, ці функції можуть бути різними. Часто попит і пропозиція задаються лінійними залежностями, наприклад

      

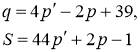
залежностями. Для того, щоб попит відповідав пропозиції необхідно

.

Звідки

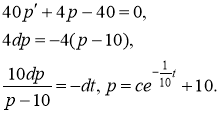   (1.18)

Припустимо, що в момент 1кг фруктів коштував 1 крб. Тоді , . Отже

.        (1.19)

Це закон зміни ціни, щоб між попитом і пропозицією була рівновага.

 

 

 

 

Економісти встановили, що швидкість зростання інвестованого капіталу в будь-який момент часу  пропорційна розміру капіталу з коефіцієнтом пропорційності, що дорівнює узгодженому відсотку  неперервного зростання капіталу. Знайти закон зростання інвестованого капіталу, враховуючи величину початкової (якщо ) інвестиції .

Розв’язання.

 Позначимо  – розмір інвестованого капіталу в момент . Тоді  – швидкість зміни величини інвестиції.

За умовою задачі маємо

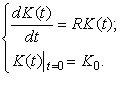
Загальним розв’язком диференціального рівняння буде функція

.

Згідно з початковою умовою при  маємо

.

Отже, розв’язком задачі Коші буде функція

.

Це означає, що за умов задачі інвестиції з часом зростають за експоненціальним законом.

 

ТИПИ ДИФЕРЕНЦІАЛЬНИХ РІВНЯНЬ ПЕРШОГО ПОРЯДКУ

Диференціальні рівняння з відокремлюваними змінними. Диференціальне рівняння першого порядку вигляду

,

де  – неперервні функції, називають рівнянням з відокремлюваними змінними. Запишемо його у вигляді

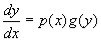
і відокремимо змінні, вважаючи, що  в області, яка розглядається. Дістанемо рівняння

.

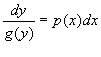Проінтегрувавши обидві частини рівняння, одержимо:

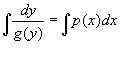 або ,

де  -– деяка первісна функції , а  – первісна функції . Таким чином, знайдено загальний інтеграл рівняння.

Такі рівняння можна записати також у вигляді

.

 

Приклад 3.

Розв’язати задачу Коші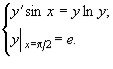 

Розв’язання.

Відокремимо змінні, вважаючи, що

:

.

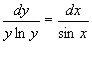Інтегруємо рівність

  ,

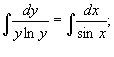
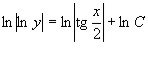звідки 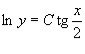 – загальний інтеграл рівняння.

Знайдемо значення довільної сталої , за якого виконуються початкові умови:

.

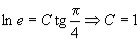Розв’язок задачі Коші має вигляд

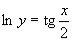 або .

 

Однорідні диференціальні рівняння першого порядку. Функцію  називають однорідною виміру , якщо виконується умова

 .

Наприклад, 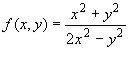 – однорідна функція нульового виміру, оскільки

.

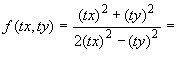
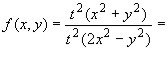
Функція  не є однорідною.

 

Однорідним диференціальним рівнянням першого порядку називають рівняння, яке можна звести до вигляду

,

де функція  однорідна функція нульового виміру.

 

Диференціальне рівняння  буде однорідним, якщо функції  і будуть однорідними функціями одного виміру.

Однорідне диференціальне рівняння першого порядку шляхом підстановки  можна звести до рівняння з відокремлюваними змінними.

 

Приклад 3.

Знайти загальний розв’язок рівняння .

Розв’язання.

Виконаємо заміну змінної за формулою

, .

Маємо рівняння 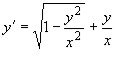 або , звідки . Відокремимо змінні та проінтегруємо:

, .

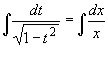Повертаючись до шуканої функції , одержуємо

.

 

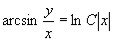Зауваження.

Розв’язуючи рівняння ми ділили обидві частини на . Очевидно, що  не є розв’язком рівняння. Якщо  отримаємо розв’язок  або , який також є розв’язком рівняння. Звідси остаточна відповідь:

 , .

 

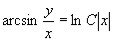Лінійні диференціальні рівняння першого порядку

Диференціальне рівняння називають лінійним диференціальним рівнянням першого порядку, якщо воно лінійне відносно невідомої функції  та її похідної .

Лінійне рівняння має вигляд

,

де  і – задані та неперервні на деякому інтервалі  функції.

Диференціальне рівняння

називають лінійним однорідним рівнянням і воно є рівнянням з відокремлюваними змінними, тобто

.

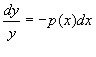Інтегруючи це рівняння, одержуємо

,

де С – додатна стала.

Знаходимо загальний розв’язок рівняння

,

де С – стала довільного знака.

Загальний розв’язок неоднорідного лінійного рівняння  будемо шукати методом варіації довільної сталої(методом Лагранжа).

Вважатимемо, що С є функція від х , тобто

.

Звідси отримуємо

.

Підставимо вирази для  і  в рівняння .

Маємо

+,

тобто .

Отже,  і загальний розв’язок неоднорідного лінійного рівняння  має вигляд

.

 

Приклад 4.

Розв’язати рівняння .

Розв’язання. Розв’яжемо спочатку однорідне лінійне рівняння , відокремивши змінні

 .

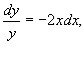
Звідки загальний розв’язок має вигляд

.

Застосуємо метод варіації довільної сталої.

, .

Підставимо вирази для  і  в рівняння

:

.

Звідси ,  (– довільна стала).

Отже, шуканий розв’язок має вигляд

.

 

Рівняння Бернуллі. Диференціальне рівняння першого порядку вигляду

,

де  та називають рівнянням Бернуллі. Його зводять до лінійного рівняння підстановкою

.

 

Приклад 5.

Розв’язати рівняння .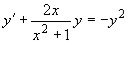

Розв’язання.

Зведемо дане рівняння до лінійного підстановкою .

Тоді

,  

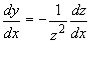
і рівняння має вигляд

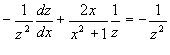 або .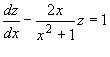

Отримали лінійне рівняння першого порядку, розв’язок якого має вигляд

 або .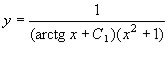

Це рівняння, крім загального розв’язку, має ще особливий розв’язок .

 

Задачі для самостійної роботи

1. Розв’язати диференціальні рівняння першого порядку

а) ; б) ;

в) ; г) .

 

 

 

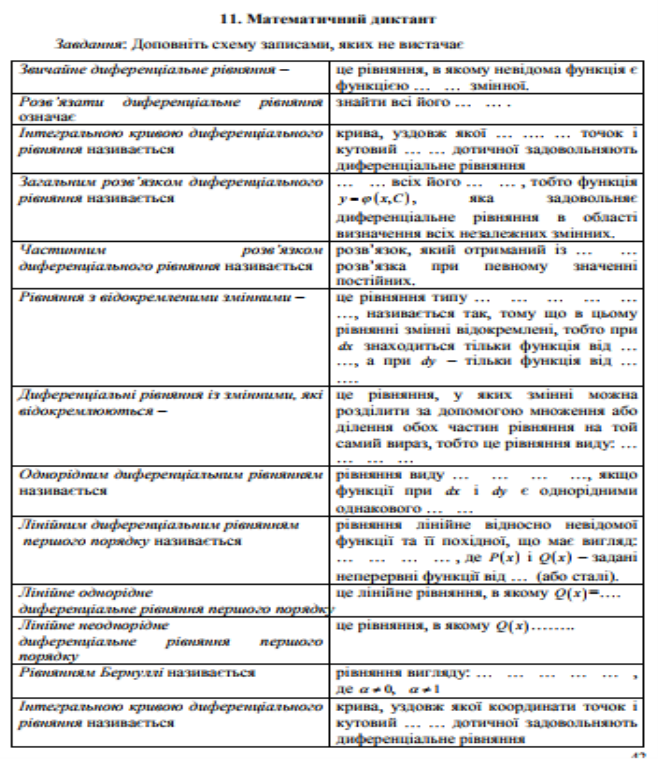
Запитання для актуалізації базових знань 1. Які рівняння називаються диференціальними? 2. Як визначити порядок ДР? 3. Що називається загальним розв’язком ДР? 4. Що називається частинним розв’язком ДР? 5. Який вигляд мають ДР з відокремлюваними змінними? 6. Сформулюйте план розв’язку ДР з відокремлюваними змінними. 7. Яка функція  f x y  ,  називається однорідною? 8. Який вигляд має однорідне ДР? 9. За допомогою якої заміни розв’язується однорідне ДР? 10. Яким методом розв’язують лінійні ДР першого порядку? 11. Навіщо інженеру знати теорему існування єдиного розв’язку задачі Коші?

 

 

 

Застосування  диференціальних  рівнянь  в  економіці.  Нехай  p t)(   –  ціна,  наприклад, на фрукти,  dt dp  – тенденція формування ціни. Тоді, як попит так  і  пропозиціябудутьфункціямивведених  величин.  Як  показує  практика,  ціфункціїможуть  бути  різними.  Часто  попит  q   і  пропозиція S задаютьсялінійнимизалежностями:     1244     ,3924 ppS    Для того, щобпопитвідповідавпропозиціїнеобхі       ppq дно( p   pp     pp 12443924 , звідки  S)        , .10 10   10 ),10(44 ,040440 10 1      t ce dp pdp pp pdt p Припустимо,  що  в  момент  t  0   1кг  фруктівкоштував p )0( 1 у.од.  Тоді c  101 , c  9 .Отже  109 10  t ep .              1 Це закон зміниціни, щобміж попитом і пропозицією була рівновага.  Як бачимо диференціальні рівняння використовуються в різних сферах  науки. 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Приклади задач з евристичними підказками для розв’язування на практичних заняттях Задача 13.1. Знайти загальний розв’язок рівняння:  2 2 1 x y x    Розв’язання: 1. Пригадаємо, що  dy y dx    и перепишемо рівняння у іншому вигляді. 2. З’ясуємо вид цього рівняння: (це рівняння з відокремлюваними змінними). 3. Помножимо обидві частини рівняння на dx . 4. Інтегруємо обидві частини рівняння. 5. Запишемо загальний розв’язок диференціального рівняння. Відповідь:    2 y x C    ln 1 , де C – довільна стала. Задача 13.2. Знайти загальний розв’язок рівняння:  x y y e    Розв’язання: 1.  Пригадаємо  ,  що  dy y dx   ,  а  також  властивості  степенів  з  однаковими  основами  m n m n a a a     та перепишемо рівняння у іншому вигляді. 2. З’ясуємо вид цього рівняння: (це рівняння з відокремлюваними змінними). 3. Помножимо обидві частини рівняння на  y dx e . 4. Інтегруємо обидві частини рівняння. 5. Запишемо загальний розв’язок диференціального рівняння. Відповідь:  ln   x y C e    , где C R  . Задача 13.3.  Знайти  загальний  розв’язок  та  особливі  розв’язки  диференціального рівняння:      2 2 y x dy x y dx 1 1 0     Розв’язання: 1. З’ясуємо вид цього рівняння: (це рівняння з відокремлюваними змінними). 2.  Перенесемо  другий  доданок  через  знак  «=»,  при  цьому  пам’ятаємо,  що  знак  змінюється на протилежний, перепишемо рівняння у іншому вигляді. 3. Розділимо обидві частини рівняння на вираз    2 2 1 1   x y . 4. Інтегруємо обидві частини рівняння. 5. Запишемо розв’язок диференціального рівняння у вигляді загального інтеграла. 6. Запишемо особливі розв’язки диференціального рівняння. 46 Відповідь:     2 2 1 1    y C x , де C – довільна стала – загальний інтеграл; x y     1, 1 – особливі розв’язки.  Задача 13.4.  Знайти  загальний  розв’язок  та  особливі  розв’язки  диференціального рівняння:   2 2 y xy dx x dy    2 0 Розв’язання: 1.  З’ясуємо  вид  цього  рівняння:  (це  однорідне  диференціальне  рівняння  першого  порядку). 2. Виділимо у лівій частині рівняння  dy dx  і перепишемо рівняння у іншому вигляді. 3. Пригадаємо, що  dy y dx    і перепишемо рівняння у вигляді  y y f x        . (для цього необхідно дріб, який стоїть у правій частині рівняння записати у вигляді  різниці двох дробів) 4.  Застосуйте  підстановку  y t y t x x    ,  звідси  y t x t       або  dy dt x t dx dx   .  Перепишемо рівняння у іншому вигляді. 5. Зробимо необхідні перетворення. 6. Отримали рівняння з відокремлюваними змінними. 7. Помножимо обидві частини рівняння на вираз    2 dx x t t  . 8. Інтегруємо обидві частини рівняння. 9. Запишемо розв’язок диференціального рівняння у вигляді загального інтеграла. 10. Запишемо особливі розв’язки диференціального рівняння. Відповідь:  y Cx y x   , де C – довільна стала – загальний інтеграл;  x y x   0, – особливі розв’язки. 47 14. Приклад професійно-спрямован