Презентація на тему: Комбінаторика

Первинні поняття комбінаторики. Перестановки, розміщення, комбінації. Біном Ньютона

Мета: Ознайомлення з початковими поняттями комбінаторики, розглянути вибірки елементів, правила суми та добутку, базові методи перестановки, розміщення, комбінації, бінома Ньютона. Вузлові питання заняття:поняття факторіалуправила суми і добуткувибіркибіном Ньютона. Формуванняпоняття

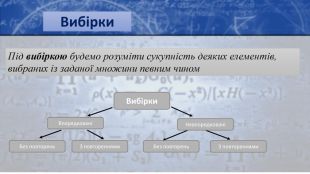
Поняття комбінаторики. Н. Бурбакі«Сьогодні ми знаємо, що, логічно кажучи, можливо вивести майже всю сучасну математику з одного джерела – теорії множин». Поняття множин це основне поняття комбінаторики, яка є одним із розділів математики. Комбінаторика – розділ математики, присвячений розв’язанню задач вибору і розміщення елементів деякої, зазвичай скінченної множини у відповідності з деякими правилами.

Історія виникнення комбінаторики35 століть назад Гра «сенет» у Древньому ЄгиптіXII – XIII ст. до н.е. Китайській рукопис «Же-ким» («Книга перестановок»)Комбінаторика у Древній ГреціїРоботи філософа Ксенократ, стоїка Хрисиппа, астронома Геппарха, математика Піфагора. Комбінаторика в країнах Сходу. Формула обчислення степеня суми двох чисел поета і математика Омара Хайяма. Комбінаторика епохи комп’ютерів. За допомогою ЕОМ стало можливим робити перебори, що раніше потребували сотень і тисяч років

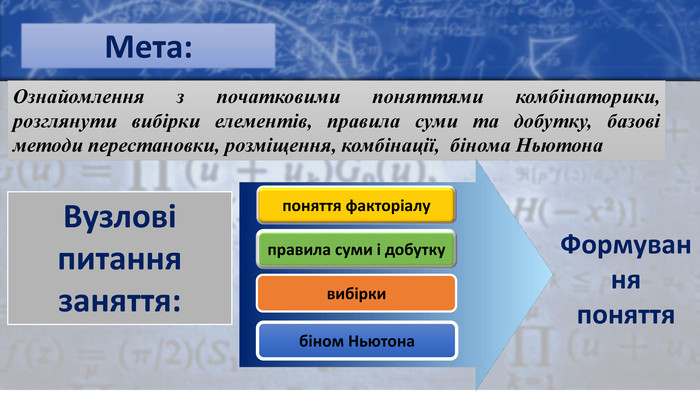
Поняття факторіалу. Факторіал - це функція, визначена на множині цілих додатних чисел і представляє собою добуток всіх натуральних чисел від 1 до n, де кожне число зустрічається лише один раз.n! = 1·2·3·4·…·(n – 1) ·n. Якщо n = 1, то f = 1! = 1. Якщо n = 2, то f = 2! = 1·2 = 2. Якщо n = 3, то f = 3! = 1·2·3 = 6. Якщо n = 4, то f = 4! = 1·2·3·4 = 24. Якщо n = 5, то f = 5! = 1·2·3·4·5 = 120. Записати зі знаком факторіала: 1 · 2 · 3 · 4 · 4 · 5 · 6 Спростити: Приклад

Операції (дії) над множинами

Правила комбінаторики. Правило добутку

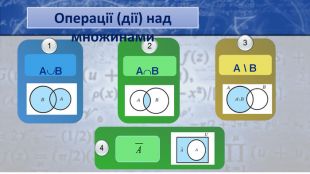
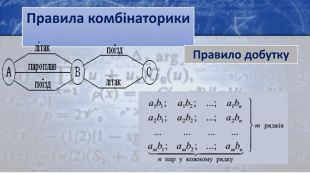
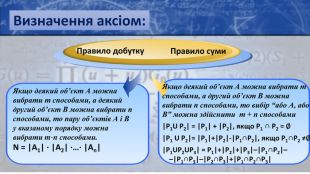
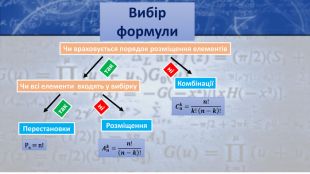
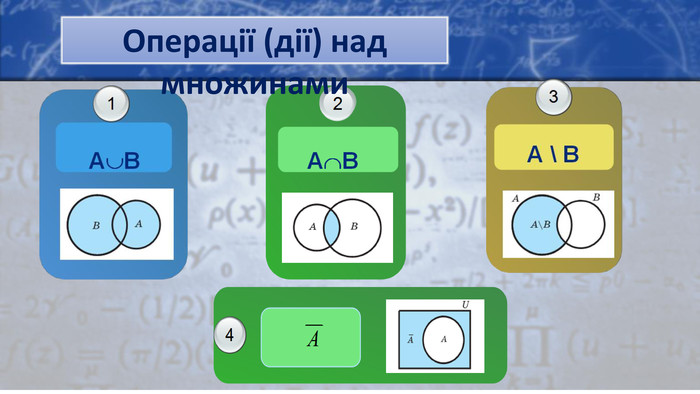
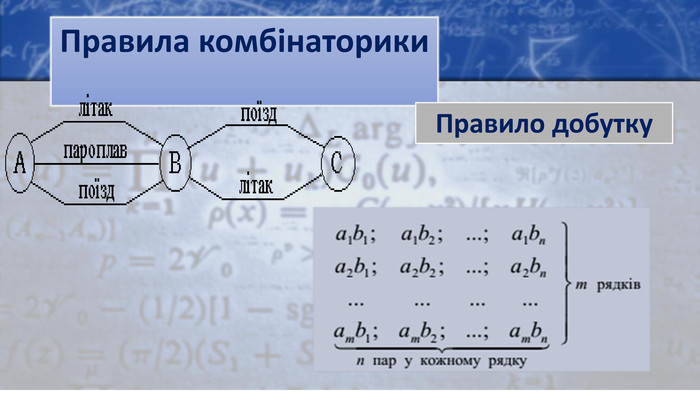
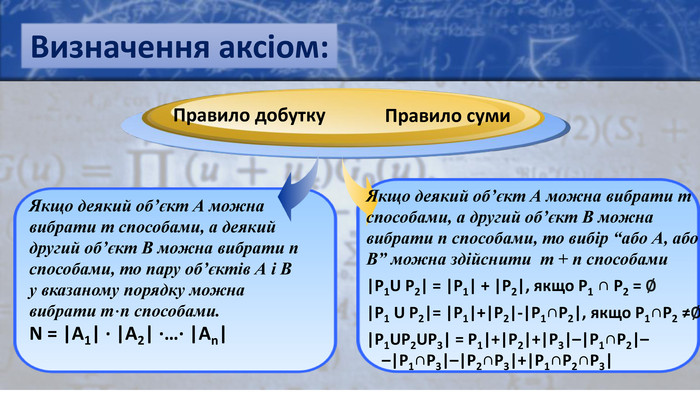
Визначення аксіом: Правило суми. Правило добутку. Якщо деякий об’єкт А можна вибрати m способами, а деякий другий об’єкт В можна вибрати n способами, то пару об’єктів А і В у вказаному порядку можна вибрати m⋅n способами. N = |A1| · |A2| ·…· |An|Якщо деякий об’єкт А можна вибрати m способами, а другий об’єкт В можна вибрати n способами, то вибір “або А, або В” можна здійснити  m + n способами|Р1 U Р2| = |Р1| + |Р2|, якщо Р1 ∩ Р2 = ∅|Р1 U Р2|= |Р1|+|Р2|-|Р1∩Р2|, якщо Р1∩Р2 ≠∅|Р1 UР2 UР3| = Р1|+|Р2|+|Р3|–|Р1∩Р2|– –|Р1∩Р3|–|Р2∩Р3|+|Р1∩Р2∩Р3|

Приклади. В урні п'ять куль з номерами 1, 2, 3, 4, 5. Виймають одну кулю і записують її номер. Кулю повертають в урну і навмання знову вибирають одну кулю і її номер записують праворуч від першої цифри. Вийде дворозрядне число. Скільки можливо таких чисел?Повернемося до прикладу 1. Нехай кулі виймають три рази. Скільки вийде тризначних чисел?Скільки існує трьохрозрядних шісткових чисел?Скільки існує п'ятизначних симетричних вісімкових чисел, тобто таких чисел, які однаково читаються як зліва направо, так і справа наліво, наприклад: 23032, 55655, 10001?У тарілці лежать 6 яблук і 4 груші. Скількома способами можна вибрати один плід? Нехай дано множини: Р1 = {1, 2, 4, 7, 9}; Р2 = {1, 4, 5, 6, 8}. Скільки елементів у множині Р1 U Р2?З 100 студентів англійську мову знають 28 осіб, німецька - 30, французьку - 42, англійську та німецьку - 8, англійську та французьку - 10, німецьку та французьку - 5, всі три мови знають 3 людини. Скільки студентів не знають жодної іноземної мови?

Вибірки. З повтореннями. Без повторень. ВпорядкованіНевпорядкованіБез повторень. З повтореннями. Вибірки. Під вибіркою будемо розуміти сукупність деяких елементів, вибраних із заданої множини певним чином

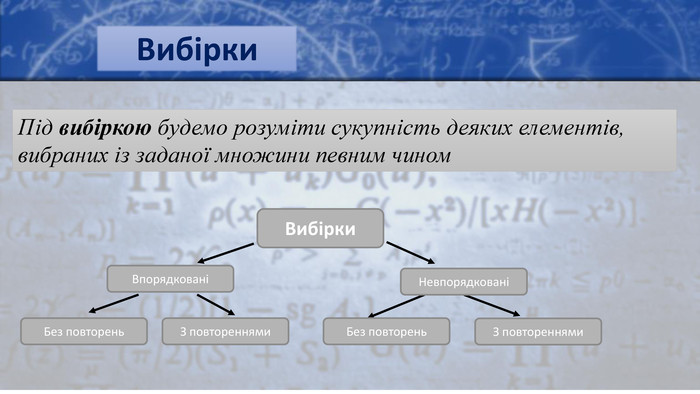
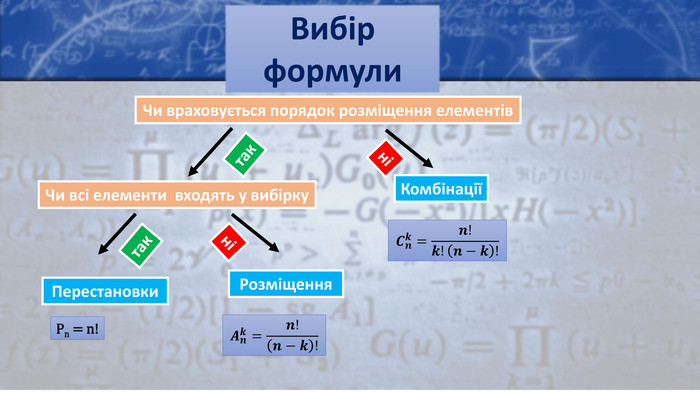
Перестановка без повторень. Впорядковані n-елементні вибірки без повторень з множини В називаються перестановками без повторень з n елементів. Формула для числа перестановок. Рn = n · (n-1) · (n-2) · ... · 3 · 2 · 1 = n!Одного разу 10 друзів зайшли до кав’ярні. Господар кав’ярні запропонував їм приходити до нього щодня і кожного разу сідати за той самий стіл по-іншому; після того, як усі способи розміщень будуть вичерпані, їх пригощатимуть у кав’ярні безкоштовно. Коли настане цей день?Приклад. Визначення

Перестановка з повтореннями. Послідовність довжини n, складена з k різних символів, перший з яких повторюється n1 раз, другий - n2 раз, третій - n3 раз, ..., k-й - nk раз (де n1 + n2 + ... + nk = n) називається перестановкою з повтореннями з n елементів. Формула для числа перестановок: 1. Скільки існує чотирибуквенних слів, у яких три літери «а» і одна буква «в»?2. Скільки різних слів можна скласти, переставляючи літери слова «ротор»?Приклади. Визначення

Розміщення без повторень. Впорядковані k-елементні вибірки без повторень з множини В називаються розміщеннями без повторень з n елементів по k елементів. Формула для числа розміщень: Скільки існує трьохрозрядних десяткових чисел, що не містять парних цифр і не містять однакових цифр?2. Є 12 ролей. Чотири артиста можуть грати будь-яку роль, і всім їм пропонується вибір. Скількома способами можна розподілити ролі між ними?Приклади. Визначення𝐴𝑛𝑘=𝑛!𝑛−𝑘! 

Розміщення з повтореннями. Впорядковані k-елементні вибірки з повтореннями з множини В називаються розміщеннями з повтореннями з n елементів по k елементів. Число розміщень з повтореннями з n елементів по k елементів позначається символом 𝐴𝑛𝑘. Формула для числа розміщень:  Скільки можна утворити чотирьохрозрядних чисел, використовуючи тільки цифри 3, 7, 8, 9, якщо повторення можливі?2. Скільки всього існує трьохрозрядних десяткових чисел, які можуть бути складені з цифр 1, 2, 4, 5, 6, 8?Приклади. Визначення𝐴𝑛𝑘=𝑛∙𝑛∙𝑛∙…∙𝑛=𝑛𝑘 

Комбінація без повторень. Невпорядковані k-елементні вибірки без повторень із множини В називаються комбінаціями без повторень з n елементів по k елементів. Формула для числа комбінацій: Скільки існує шестирозрядних двійкових чисел, що містять три одиниці?2. Скільки існує п'ятизначних десяткових чисел, в кожному з яких цифри йдуть:1) у порядку зростання зліва направо?2) в порядку зменшення зліва направо?Приклади. Визначення𝐶𝑛𝑘=𝑛!𝑘!𝑛−𝑘! 

Комбінація з повтореннями. Невпорядковані k-елементні вибірки з повтореннями із множини В називаються комбінаціями з повтореннями з n елементів по k елементів. Формула для числа комбінацій: У магазині є 4 види цукерок: «Каракум», «Ромашка», «Червоний мак», «Сніжинка». Потрібно купити 10 цукерок в будь-якому поєднанні з перерахованих. У три ящики необхідно розкласти 30 гайок так, щоб у кожному ящику виявилося хоча б по п'ять гайок. Скількома способами це можна зробити?Приклади. Визначення𝐶𝑛𝑘=С𝑛+𝑘−1𝑘=С𝑛+𝑘−1𝑛−1 

Вибір формули. Чи враховується порядок розміщення елементівтакніЧи всі елементи входять у вибірку. КомбінаціїтакніПерестановки. Розміщення𝑪𝒏𝒌=𝒏!𝒌!𝒏−𝒌! Pn = n!𝑨𝒏𝒌=𝒏!𝒏−𝒌! 

Контрольні запитання. Назвіть правило суми. Назвіть правило добутку. Що таке вибірка?Які бувають вибірки?Що називаємо розміщеннями і за якими формулами знаходяться?Що називаємо перестановками і за якими формулами знаходяться?Що називаємо комбінаціями і за якими формулами знаходяться?Що називаємо біномом Ньютона?Роль комбінаторики в сучасному світі?Домашнє завдання: опрацювати конспект, л.1 с.5-17, л.2 с. 59-70.

Властивості комбінацій без повторень. Порівняємо праву і ліву частину, записавши їх у розгорнутому вигляді:𝐶𝑛𝑘=𝑛!𝑘!𝑛−𝑘! 𝐶𝑛𝑛−𝑘=𝑛!𝑛−𝑘!𝑛−𝑛−𝑘!=𝑛!𝑛−𝑘!𝑘! 1). 𝐶𝑛𝑘=𝐶𝑛𝑛−𝑘 2).  𝐶𝑛𝑘=𝐶𝑛−1𝑘−1+𝐶𝑛−1𝑘 Щоб визначити рівність двох частин рівняння праву частину перетворимо:𝐶𝑛−1𝑘−1+𝐶𝑛−1𝑘=𝑛−1!𝑛−𝑘!𝑘−1!+𝑛−1!𝑛−𝑘−1!𝑘!=𝑛−1!𝑘𝑛−𝑘!𝑘𝑘−1!++𝑛−1!𝑛−𝑘𝑛−𝑘−1!(𝑛−𝑘)𝑘!=(𝑛−1)!(𝑛+𝑛−𝑚)𝑛−𝑘!𝑘!=𝑛!𝑛−𝑘!𝑘!=𝐶𝑛𝑘 

Трикутник Паскаля. Дана тотожність дозволяє послідовно виписувати числа 𝐶𝑛𝑘 у вигляді таблиці, яка називається трикутником Паскаля: 1 11 2 11 3 3 11 4 6 4 11 5 10 10 5 1

Біном Ньютона𝐶𝑛0+𝐶𝑛1+𝐶𝑛2+𝐶𝑛3+…+𝐶𝑛𝑘=𝑖=0𝑛С𝑛𝑖=2𝑛Для доказу скористаємося функцією (1 + х)n для чисел С𝑛𝑖, де i = 0,1,2, ..., n. Відомо, що: (1+𝑥)𝑛=𝐶𝑛0+𝐶𝑛1𝑥+𝐶𝑛2𝑥2+𝐶𝑛3𝑥3+…+𝐶𝑛𝑘𝑥𝑛=𝑖=0𝑛С𝑛𝑖𝑥𝑖 

Записати з використанням знака факторіала: 1 · 2 · 3 · 4 · 5 · 7 · 8 · 9 · 10. Записати зі знаком факторіала: 1 · 3 · 5 · 6 · 7 · 8 Спростити: Перестановки без повторень. Характеристичні ознаки: предмети різні, всі місця зайняті, порядок елементів важливий. Скільки існує трьохрозрядних десяткових чисел, що не містять цифр, які повторюються, якщо використовуються тільки цифри 3, 5, 9?Скільки різних слів можна скласти з літер слова «кілометр», якщо під словом розуміти всяку послідовність з восьми букв? У класі навчається 8 юнаків. Скількома способами можна їх вишикувати у шеренгу?

Розміщення з повтореннями Характеристичні ознаки розміщень: предмети і місця різні, порядок елементів важливий, усі n місць необхідно зайняти, 0 ≤ n ≤ m. Дано множину букв: А = {а, б, в, г, д, е}. Скільки двох- і трибуквених слів можна скласти з цих букв?Скільки існує п’ятирозрядних чисел шісткової системи числення?Учню треба скласти 4 екзамени на протязі 8 днів. Скількома способами це можна зробити?10 спортсменів розігрують одну золоту, одну срібну і одну бронзову медалі. Скількома способами ці медалі можуть бути розподілені між спортсменами?Комбінації без повторень. Характеристичні ознаки: порядок вибору елементів не має значення, предмети різні, 0 ≤ n ≤ m. Для проведення іспиту створюється комісія із двох викладачів. Скільки різних комісій можна скласти із п’яти викладачів?Із 20учнів треба виділити 6 для чергування. Скількома способами це можна зробити?На полиці є 35 книжок. Скількома способами можна вибрати дві із них?

Нехай множина В складається з трьох елементів В={a, b, c}. Виписати: а) двоелементні розміщення без повторень, б) двоелементні розміщення з повтореннями, в) двоелементні комбінації без повторень, г) двоелементні комбінації з повтореннями, д) перестановки без повторень. Підрахувати кількість вибірок кожного виду.