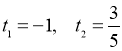Методична розробка "Розв’язування тригонометричних рівнянь способами зведення до однієї тригонометричної функції, розкладання на множники»"
Анотація
Дана методична розробка спрямована на пробудження інтересу в учнів до навчання, ефективного засвоєння навчального матеріалу використовувалися різноманітні інтерактивні технології.
В розробці використовувалися усні та письмові форми роботи. Перевірка домашнього завдання була проведена у вигляді бліц-опитування, яке передбачало перевірку відповідей учнів на питання з попередніх тем «Обернені тригонометричні функції», «Найпростіші тригонометричні рівняння». Для виконання наступної інтерактивної вправи «Встановіть відповідність «Рівняння - корені»» учні об’єднувались в групи і після колективного обговорення давали письмову відповідь на заздалегідь підготовлених бланках.
Використання інтерактивних методів навчання у процесі викладання математики позитивно позначається на рівні засвоєння навчального матеріалу, ефективності та результативності роботи учнів.
Зміст
- Вступ
- Теоретичні відомості: «Найпростіші тригонометричні рівняння»
- План уроку на тему: «Розв’язування тригонометричних рівнянь способами зведення до однієї тригонометричної функції, розкладання на множники»
- Висновки
- Використана література
- Додатки
- Вступ
Свого часу велася запекла дискусія з приводу означення поняття тригонометричне рівняння. Тригонометричним пропонували називати:
- рівняння, в якому змінна входить лише під знак тригонометричної функції (в такому разі рівняння виду sin х+х=0 не належить до тригонометричних; його пропонували називати трансцендентним);
- рівняння, в якому змінна входить під знак тригонометричної функції.
З цього приводу слід погодитись з думкою С. І. Новосьолова, який вважав, що розходження в означеннях тригонометричного рівняння не є принциповими. Важливо одне – немає загального методу розв'язування тригонометричних рівнянь. Слід наголосити на принциповій відмінності тригонометричних рівнянь від алгебраїчних: тригонометричні рівняння, в яких змінна входить лише під знак тригонометричної функції, або зовсім не мають розв'язків, або мають їх безліч. Це пов'язано з властивістю періодичності тригонометричних функцій.
Тригонометричними рівняннями називаються рівняння, у яких невідома (змінна) входить лише під знак тригонометричної функції.
Наприклад: sin x – cos x = 0; 2sin x+cos x = sin2 2x; cos 4xcos 2x = cos 5x; tg 5x + tg 3x = 0.
У курсі математики тригонометричні рівняння розглядаються на множині дійсних чисел. При розв’язанні тригонометричних рівнянь спочатку потрібно визначити область допустимих значень невідомого, враховуючи, що функції cos x i sin x визначені при всіх дійсних значеннях x, функція tg x визначена при ![]() , де k ∈ Z, і функція ctg x визначена при,
, де k ∈ Z, і функція ctg x визначена при, ![]() k∈Z.
k∈Z.
Загального методу розв’язання тригонометричних рівнянь не існує, і пошук розв’язання в кожному конкретному випадку потребує певної майстерності у виконанні тригонометричних перетворень, знання тригонометричних формул. Потрібно зазначити, що при розв’язанні найпростіших тригонометричних рівнянь запис розв’язків має однозначну форму. У більш складних прикладах форма запису множини розв’язків неоднозначна, але ідентичність різних форм запису завжди можна довести за допомогою тотожних перетворень. Різна форма запису пояснюється різними методами, за допомогою яких розв’язується дана задача. Розв’язування різних типів тригонометричних рівнянь в основному зводиться до розв’язання найпростіших тригонометричних рівнянь.
- Теоретичні відомості: «Найпростіші тригонометричні рівняння»
Не існує загального способу розв'язування будь-якого тригонометричного рівняння. Однак деякі способи розв'язування окремих видів тригонометричних рівнянь можна вказати. Як правило, розв'язування будь-якого тригонометричного рівняння зводиться до розв'язування найпростіших рівнянь sin x = a, cos x = a, tg x = a. Рівняння ctg x= а рівносильне рівнянню tg x = 1/a тому немає потреби розглядати його окремо.
Розв’язати найпростіше тригонометричне рівняння — означає знайти множину всіх кутів, що мають дане значення тригонометричної функції
Розглянемо розв'язування найпростіших тригонометричних рівнянь.
Рівняння sin x = a. Розв'яжемо це рівняння спочатку графічно, побудувавши в одній системі координат графіки функцій у = sin x і у = а.
Якщо |а| > 1, тобто при а > 1 і а < -1, пряма і синусоїда не перетинаються. Тому рівняння sin x = а не має розв'язків (рис. 1.1.).
Знайдемо розв'язки, якщо |а| ≤ 1, тобто коли -1 ≤ |а| ≤ 1, на відрізку [-π; π], а потім скористаємося періодичністю функції синус.
Нехай 0 < а < 1. Як видно з рисунку, пряма у = а за цієї умови перетинає синусоїду у двох точках P1 і Р2, абсциси яких належать проміжку (0; π).
Оскільки розв'язання рівняння sin x = а зводиться до знаходження числа (геометрично кута чи дуги), синус якого дорівнює а, то цим числом є arcsin а, якщо воно міститься на проміжку[-; . Отже, абсцисою точки P1 є arcsin a. Абсцису точки Р2 запишемо через arcsin а як різницю π – arcsin a.
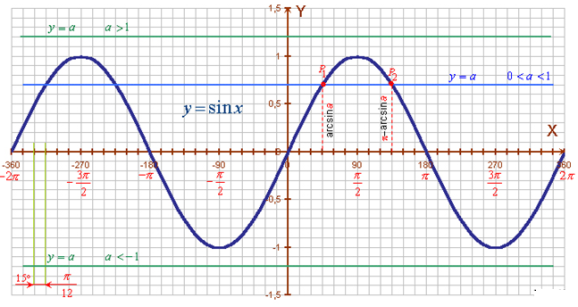
Рис. 1.1.
Якщо додати до знайдених розв'язків період 2n, то при 0 < а < 1 дістанемо всі розв'язки рівняння sin x = а у вигляді двох множин
x = arcsin а + 2nπ, n Ζ; (1)
x = arcsin a + 2nπ = - arcsin a + (2n+1) π, n Ζ. (2)
Об'єднуючи ці дві формули в одну, дістали загальну формулу розв'язків рівняння: x = (- l)k arcsin a +kπ, k Ζ. (3)
Якщо a = 0, то пряма у = а перетинає синусоїду в точках, абсциси яких дорівнюють nπ. Отже, рівняння sin x = 0 має множину розв'язків х = n, де nΖ.
Якщо a = 1, то пряма дотикається до синусоїди у точках з абсцисами x = 2n. Таким чином, рівняння sin x = 1 має множину розв'язків
x = /2+2n, n Ζ. Якщо a = - 1, x = - π/2+ 2nπ, n Ζ.
Неважко довести, що коли а = 0, а =1 і а = -1, ті ж самі множини розв'язків можна знайти і за загальною формулою (3).
Загальну формулу розв'язків рівняння sinx = а, можна знайти і за допомогою одиничного кола.
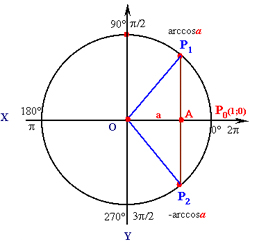
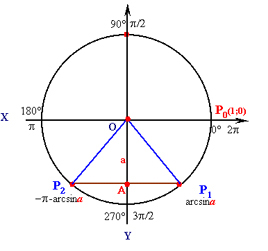
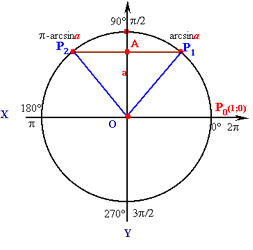
Нехай 0 < а < 1. Оскільки а як значення синуса є ординатою точки одиничного кола, то відкладемо на осі Оу відрізок, що дорівнює а, і через кінець його А проведемо пряму, паралельну осі Ох (рис. 1.2.).
![]()
![]() Вона перетне коло у двох точках Р1 і Р2. Оскільки треба знайти таке число (кут або дугу), синус якого дорівнює а, то таких чисел, яким відповідають точки Р1 і Р2 одиничного кола, виявилось два. Перше з них, яке міститься на проміжку (-π/2; π/2),є arcsin а, а друге дорівнює π – arcsin а. Враховуючи періодичність функції синус, дістанемо дві множини розв'язків рівняння sin х = а , якщо 0 < а < 1:
Вона перетне коло у двох точках Р1 і Р2. Оскільки треба знайти таке число (кут або дугу), синус якого дорівнює а, то таких чисел, яким відповідають точки Р1 і Р2 одиничного кола, виявилось два. Перше з них, яке міститься на проміжку (-π/2; π/2),є arcsin а, а друге дорівнює π – arcsin а. Враховуючи періодичність функції синус, дістанемо дві множини розв'язків рівняння sin х = а , якщо 0 < а < 1:
х = arcsin а + 2nπ, n ![]() Ζ,
Ζ,
x = π – arcsin а + 2nπ = - arcsin а+(2n +1) π.
Після їх об'єднання дістанемо загальну формулу розв'язків
х = (- 1)k arcsin а +kπ, k ![]() Ζ
Ζ
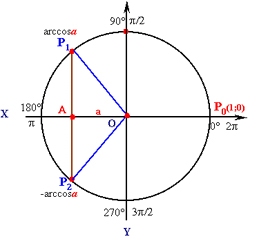
Нехай -1 < а < 0. Відповідні точки Р1 і Р2, що зображують числа на одиничному колі, належать нижньому півколу (рис. 1.3.). Точка Р1 зображує число, яке належить проміжку (-π/2; π/2), і є arcsin a. Точка Р2 зображує число, яке дорівнює - π - arcsina. Враховуючи періодичність синуса, дістанемо дві множини розв'язків рівняння sin x = a, якщо -1 < a < 0:
x = arcsi n a +2nπ, n ![]() Ζ,
Ζ,
x = - x – arcsin a + 2nπ = – arcsin a + (2n - 1)π.
Об'єднуючи їх, дістанемо загальну формулу розв'язків рівняння:
x = (- l)k arcsin a + kπ, k ![]() Ζ.
Ζ.
Рівняння cos x = a. Розв'язування його графічним способом показує (рис. 1.4.), що при |a| > 1 рівняння не має розв'язків. Знайдемо розв'язки рівняння на проміжку [- π; π], довжина якого дорівнює періоду 2π.
Нехай 0 < a < 1. Проведемо пряму у = a. Вона перетне графік функції у = соs x на відрізку [- π; π] у двох точках Р1 і Р2. Оскільки треба знайти таке число (кут або дугу), косинус якого дорівнює a, то таких чисел, яким відповідають точки Р1 і Р2, виявилось два. Перше з них належить проміжку (0; π) і є arccos a, а друге — протилежне йому і дорівнює - агссоs a внаслідок парності функції косинус. Враховуючи періодичність функції косинус, дістанемо дві множини розв'язків рівняння cos x = a, якщо 0 < a < 1 :
x = ± arccos a + 2nπ, n ![]() Ζ. (4)
Ζ. (4)
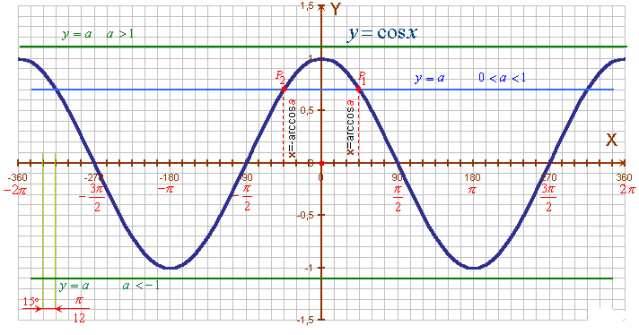
Рис. 1.4.
Нехай -1 <a < 0. З рис 1.5 видно, що пряма у = a перетинає графік косинуса у двох точках Р1 і Р2 . Абсциса точки Р1 належить проміжку (0; π) і тому дорівнює arccos a, абсциса другої точки Р2 дорівнює - arccosa. Додаючи до знайдених розв'язків період 2nπ, дістанемо дві множини розв'язків, які можна записати у вигляді однієї формули
x = ± arccos a + 2nπ, n ![]() Ζ.
Ζ.
Отже, дістали ту саму загальну формулу (4) розв'язків рівняння cos x = a, якщо -1 < a < 0.
Якщо a = 0, пряма у = a перетинає графік косинуса у точках з абсцисами π/2 + nπ, n ![]() Ζ. Якщо a = 1, пряма дотикається до графіка косинуса у точках з абсцисами 2nπ, n
Ζ. Якщо a = 1, пряма дотикається до графіка косинуса у точках з абсцисами 2nπ, n ![]() Ζ, якщо a = - 1, дотикається у точках з абсцисами (2n + 1) π, n
Ζ, якщо a = - 1, дотикається у точках з абсцисами (2n + 1) π, n ![]() Ζ.
Ζ.
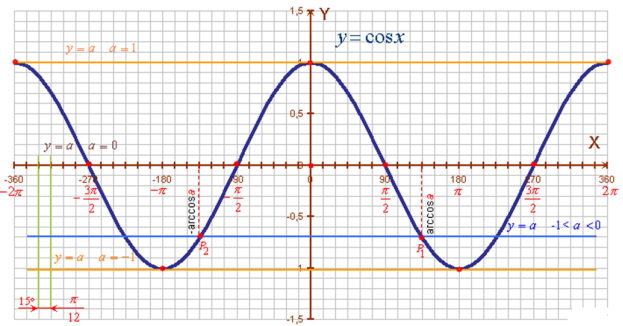
Рис. 1.5.
Доцільно запам'ятати «особливу» форму запису розв'язків рівняння cosх = a для окремих випадків:
якщо cosx = 0, то х = π/2+ nπ, n ![]() Ζ;
Ζ;
якщо cosx = 1, то х = 2nπ, n ![]() Ζ;
Ζ;
якщо cosx = -1, то х = -π+2nπ, n ![]() Ζ.
Ζ.
Неважко показати, що ці самі множини розв'язків для окремих значень a можна дістати із загальної формули розв'язків x = ± arccos a + 2nπ. Справді, якщо a = 0, arccos a = π/2 , a x = ± π/2 + 2nπ = (4n ± 1) π/2, n![]() Ζ.
Ζ.
Проте вираз 4n ± 1, якщо n![]() Ζ , дає множину всіх непарних чисел, як і вираз 2n+ 1, що входить до формули x = π/2 + nπ = (2n+1) π/2.
Ζ , дає множину всіх непарних чисел, як і вираз 2n+ 1, що входить до формули x = π/2 + nπ = (2n+1) π/2.
Загальну формулу розв'язків рівняння cosx = a, якщо |a| ≤ 1, за допомогою одиничного кола можна вивести так само, як і для рівняння sin x = a.
Як видно з рисунка 1.6., якщо 0 < a < 1, пряма, паралельна осі Оу і проведена у кінці А відрізка осі абсцис завдовжки a, перетинає коло у двох точках р1 і р2. Точка р1 відповідає числу, що належить проміжку (0;π), тобто є arccos a, друга точка р2 відповідає числу - агссоsa внаслідок парності функції косинус. Додаючи період до обох чисел, дістанемо загальну формулу (4) розв'язків рівняння cos x=a, якщо 0 < a < 1 :
|
|
|
х = ± arccos a + 2nπ, n ![]() Ζ.
Ζ.
Якщо -1 < a <0, пряма, проведена у кінці відрізка ОА паралельно осі Оу, теж перетинає коло у двох точках р1 і р2 (рис. 1.7.). Точка р1 відповідає числу, що належить проміжку (0; π), і є аrccos a, а р2 відповідає числу – агссоs a. Додаючи період до обох чисел, знов дістанемо ту саму загальну формулу розв'язків рівняння cos x = a.
Рівняння tg x = a. Оскільки областю значень функції у = tg x є множина всіх дійсних чисел, то знайдемо розв'язки рівняння при будь-якому a па проміжку (-π/2; π/2) , довжина якого дорівнює періоду π, а потім скористаємося періодичністю функції тангенса.
Графічний спосіб розв'язування рівняння tg x = a (рис. 1.8.) показує, що на інтервалі (- π/2; π/2) пряма у = a перетинає графік тангенса лише в одній точці, абсцисою якої є arctg а. Враховуючи періодичність функції у = tg x, дістанемо загальну формулу розв'язків рівняння tg x = а, тобто множину
x = arctgа + nπ, n ![]() Ζ. (5)
Ζ. (5)
Розв'язування рівняння tgx =а за допомогою одиничного кола на проміжку (- π/2; π/2) приводить до тієї самої множини. Оскільки tg а — це ордината точки Та перетину прямої ОРа з лінією тангенсів (рис. 1.9.), а пряма ОТа перетинає одиничне коло у двох точках Ра і Ра1, то в інтервал (- π/2; π/2) потрапляє лише одна з них Ра яка відповідає числу arctg а. Всі інші розв'язки дістанемо, додавши до цього числа період nπ, n ![]() Ζ, тобто x = arctg а+nπ.
Ζ, тобто x = arctg а+nπ.
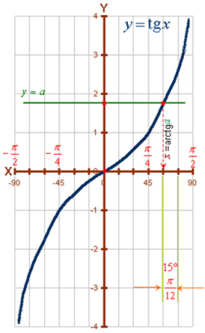
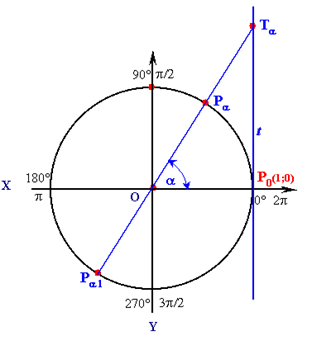
Рис. 1.8. Рис. 1.9.
Отже, маємо загальні розв'язки трьох найпростіших тригонометричних рівнянь: sin x = а, x = (- l)n arcsin а + nπ, n ![]() Ζ,
Ζ,
cos x =а, x = arccos а + 2nπ, n ![]() Ζ,
Ζ,
tg x = а, x = arctg а +nπ, n ![]() Ζ.
Ζ.
План уроку
Тема програми: Тригонометричні функції
Мета:
Навчальна: перевірити рівень засвоєння попереднього навчального матеріалу, ознайомити з іншими способами розв’язування тригонометричних рівнянь, формувати уміння і навички розв’язувати тригонометричні рівняння, відмінні від найпростіших, удосконалити уміння розв’язувати найпростіші тригонометричні рівняння.
Розвиваюча: розвивати пізнавальний інтерес, уміння використовувати сформовані знання, навики і вміння, розвивати культуру мовлення, логічне мислення, пам'ять, вміння раціонально використовувати час та оволодівати принципами організації праці, допитливість, ініціативність.
Виховна: виховувати працелюбність, прививати бажання мати якісні глибокі знання, виховувати зібраність, організованість, відповідальність, увагу, культуру міжособистісного спілкування, вміння співпрацювати в колективі.
Тип уроку: комбінований
Обладнання: таблиці, роздатковий матеріал, презентації, мультимедійне обладнання.
Хід уроку
І. Організаційний момент
Привітання; перевірка наявності учнів у класі;
організація готовності учнів до уроку.
ІІ. Актуалізація опорних знань
- Учні отримують картки самоконтролю і учитель пояснює як треба їх заповнювати. Шановні учні! Працюємо в режимі накопичення балів. Кожний отримає картку самоконтролю, куди ви будете записувати бали, отримані вами за виконання різних завдань протягом уроку. В кінці уроку ви підсумуєте кількість набраних балів і вчитель оголосить результати (або віддаєте картки самоконтролю вчителю).
Картка самоконтролю
Прізвище, ім’я_______________________
Група___________ Дата_____________
|
№ п/п |
Види діяльності |
Бали |
|
1 |
Бліц-опитування ( по 1 балу) |
|
|
2 |
Відповідність «Рівняння-корені» (по 0,5 бала за кожну відповідність) |
|
|
3 |
«Чи знаєте Ви…?» (по 0,5 бала за формулу) |
|
|
4 |
Розв’язування рівнянь: |
|
|
|
№4 |
|
|
|
№5 |
|
|
|
№6 |
|
|
|
№7 |
|
|
5 |
Додаткові бали |
|
|
|
Оцінка |
|
 Французький математик, фізик, філософ Анрі Пуанкаре сказав: «Наука складається з фактів, як будинок із каменів, але набір фактів ще не наука, так само, як купа каміння ще не будинок». Ви знаєте вже багато фактів з тригонометрії, а саме графіки та властивості тригонометричних функцій, вивчили велику кількість тригонометричних формул, знаєте як розв’язувати найпростіші тригонометричні рівняння і нашим сьогоднішнім завданням буде навчитись застосовувати ці факти (знання) при розв’язуванні більш складних тригонометричних рівнянь (іншими словами, маючи купу каміння будемо будувати будинок).
Французький математик, фізик, філософ Анрі Пуанкаре сказав: «Наука складається з фактів, як будинок із каменів, але набір фактів ще не наука, так само, як купа каміння ще не будинок». Ви знаєте вже багато фактів з тригонометрії, а саме графіки та властивості тригонометричних функцій, вивчили велику кількість тригонометричних формул, знаєте як розв’язувати найпростіші тригонометричні рівняння і нашим сьогоднішнім завданням буде навчитись застосовувати ці факти (знання) при розв’язуванні більш складних тригонометричних рівнянь (іншими словами, маючи купу каміння будемо будувати будинок).
Тож, закликаю вас до активної співпраці, будьте зосереджені, уважні і тоді ви досягнете успіху і високих результатів.
Як казав французький письменник, актор Мольєр: «Як приємно дізнатися, що ти чогось навчився». Перевіримо, чого ж ви навчилися?
ІІІ. Перевірка домашнього завдання
- Чи виникли труднощі під час виконання домашнього завдання?
Щоб вірно розв’язувати тригонометричні рівняння потрібно знати відповіді на ряд питань. Перевірку теоретичного матеріалу виконаємо із застосуванням бліц-опитування (зошити закриті).
Бліц-опитування (усна перевірка знань, фронтальна робота)
На екрані буде з’являтись запитання – учні дають відповідь. Хто перший підняв руку, той має право відповідати. За кожну правильну відповідь нараховується 1 бал, який вписуєте до картки самоконтролю. Доповнення також оцінюється. Увага на екран!
Запитання для учнів:
- Які рівняння називаються тригонометричними?
Рівняння, у яких невідоме (змінна) входить лише під знак тригонометричної функції.
- Які рівняння називаються найпростішими?
Рівняння виду ![]()
![]()
-
При якому значенні
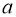 тригонометричні рівняння
тригонометричні рівняння 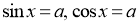 мають розв’язки?
мають розв’язки?
Якщо ![]()
-
При якому значенні
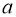 тригонометричні рівняння
тригонометричні рівняння 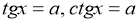 мають розв’язки?
мають розв’язки?
При будь-якому ![]() з множин дійсних чисел,
з множин дійсних чисел, ![]()
-
Що таке
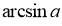 ?
?
Арксинусом числа ![]() називається таке число (кут) з проміжку
називається таке число (кут) з проміжку 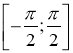 , синус якого дорівнює
, синус якого дорівнює ![]()
-
Що таке
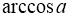 ?
?
Арккосинусом числа ![]() називається таке число (кут) з проміжку
називається таке число (кут) з проміжку ![]() , косинус якого дорівнює
, косинус якого дорівнює ![]()
-
Що таке
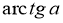 ?
?
Арктангенсом числа ![]() називається таке число (кут) з проміжку
називається таке число (кут) з проміжку 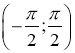 , синус якого дорівнює
, синус якого дорівнює ![]()
-
Що таке
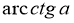 ?
?
Арккотангенсом числа ![]() називається таке число (кут) з проміжку
називається таке число (кут) з проміжку ![]() , котангенс якого дорівнює
, котангенс якого дорівнює ![]()
-
Чому дорівнює
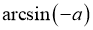 ?
?
![]()
-
Чому дорівнює
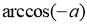 ?
?
![]()
-
Чому дорівнює
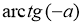 ?
?
![]()
-
Чому дорівнює
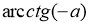 ?
?
![]()
- Яка особливість розв’язку тригонометричних рівнянь?
Як правило або зовсім не мають розв’язків або мають їх безліч.
14. Внаслідок якої властивості тригонометричних функцій тригонометричні рівняння мають безліч розв’язків?
Періодичності
Встановіть відповідність «Рівняння - корені»
(групова, письмова робота)
Нагадую учням, що на минулому занятті були розглянути види найпростіших тригонометричних рівнянь та формули для отримання їх коренів (розв’язки), які вони повинні були вивчити на сьогодні. Для перевірки знань пропонується встановити відповідність між рівняннями і коренями.
Для виконання цього завдання необхідно об’єднатися в групи по 4 учні. Кожна група отримує заздалегідь підготовлений один бланк, де вони вписують свої прізвища. Після колективного обговорення записують відповіді. Представник кожної групи учнів передає бланк із відповідями вчителю. Вчитель висвічує правильні відповіді на екрані і оголошує результати (перевірка за допомогою учнів). Ті учні, які вірно виконали завдання вписують до картки самоконтролю по 0,5 бала за кожну вірно встановлену відповідність.

 Увага на екран!
Увага на екран!
Вправа «Чи знаєте Ви…?» (усна, фронтальна робота)
Наступне завдання дозволить перевірити чи знають учні тригонометричні формули Знання цих формул знадобляться під час вивчення нового матеріалу. Хто перший підняв руку, той має право відповідати. За кожну правильну відповідь нараховується 0,5 бала, який вписується до картки самоконтролю.
Увага на екран!

Вчитель робить висновок про рівень засвоєння навчального матеріалу, називає прізвища активних учнів. Видно, що вони вчать матеріал, готуються до занять і виконують домашні завдання – це добре. «Все ж таки ви чогось навчились». Інших учнів вчитель закликає, щоб вони активніше приймали участь у роботі на занятті.
ІV. Мотивація навчальної діяльності
У даний час ви вивчаєте один із розділів математики «Тригонометрія», вивчення якого вимагає величезного напруження для осмислення, запам’ятовування. Виникає питання: для чого потрібна тригонометрія? Як вона використовується в нашому світі, житті? З чим може бути пов’язана тригонометрія? І ось відповіді на ці запитання.
Тригонометрія (це і тригонометричні функції, формули, рівняння, нерівності) використовується в астрономії (особливо для розрахунків положення небесних об’єктів), в морській і повітряній навігації, в теорії музики, в акустиці, оптиці, аналізі фінансових ринків, в електроніці, статистиці, біології, медичній візуалізації, наприклад, при проведенні томографії та ультразвуку, в хімії, сейсмології, архітектурі, в комп’ютерній графіці (при розробці комп’ютерних ігор), картографії, кристалографії та багатьох інших областях.
Вчитель акцентує увагу учнів на широкому застосуванні тригонометрії в науці і техніці, в навколишньому середовищі і робить висновок про актуальність теми розв’язування тригонометричних рівнянь.
V. Повідомлення теми, мети, плану заняття
На сьогоднішньому і наступних заняттях ми розглянемо різні способи розв’язування тригонометричних рівнянь, які відрізняються від найпростіших. Сьогодні ви познайомитесь з такими способами розв’язування тригонометричних рівнянь як зведення до однієї тригонометричної функції і розкладання на множники.
Викладач оголошує тему, мету, план заняття, учні записують в зошити тему, план заняття.
Для розуміння наступного потрібно розуміння попереднього. Дуже ефективною для проведення повтору (узагальнення, систематизації) є вправа «Асоціативний кущ».
Учням пропонується скласти «асоціативний кущ», ключовим словом (поняття, термін) якого є «рівняння». Учні мають згадати все, що виникає в пам’яті стосовно цього слова. Спочатку виникають найстійкіші асоціації, потім другорядні. Вчитель або учень фіксує відповіді у вигляді своєрідного «куща», який поступово зростає. Отже, на дошці перед очами учнів виникає за їхніми відповідями цікавий «кущ» на «гілках» якого знаходяться відомості про це поняття, слово.
Очікувані відповіді учнів: алгебраїчне, квадратне, дробове, тригонометричне найпростіше, неповне, повне, невідоме, корені, розв’язування, дискримінант, коефіцієнт, скласти, теорема Вієта.
Для усвідомлення специфіки розв’язування тригонометричних рівнянь необхідно пригадати які типи рівнянь і методи їх розв’язування знають учнів.
Очікувані відповіді: лінійні, квадратні, дробові.
Для розв’язування цих відомих рівнянь користуються заздалегідь виведеними формулами або виробленими алгоритмами, що значно спрощує роботу. Наприклад, учні знають, що зведене квадратне рівняння можна розв’язувати двома способами: за дискримінантом або за теоремою Вієта.
Настанова викладача (осмислення й поглиблення особливостей розв’язування тригонометричних рівнянь)
- Особливістю розв’язування тригонометричних рівнянь є те, що загальних методів, способу не існує.
- Що вони (рівняння) або зовсім не мають розв’язків, або мають безліч, внаслідок періодичності (про що ми вже згадували).
- Існує дуже багато тригонометричних рівнянь, і самих найрізноманітніших, тому і способів розв’язування існує багато.
 Як казав видатний італійський вчений Леонардо да Вінчі: «Якщо запастися терпінням і проявити старання, то посіяне насіння знання неодмінно дасть добрі сходи»
Як казав видатний італійський вчений Леонардо да Вінчі: «Якщо запастися терпінням і проявити старання, то посіяне насіння знання неодмінно дасть добрі сходи»
VІ. Вивчення нового матеріалу
Увага на екран!
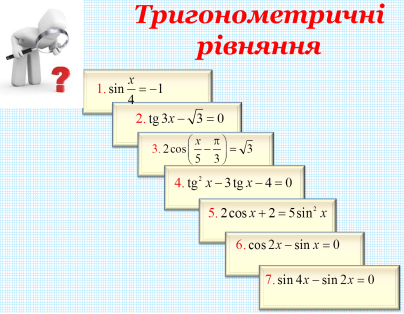
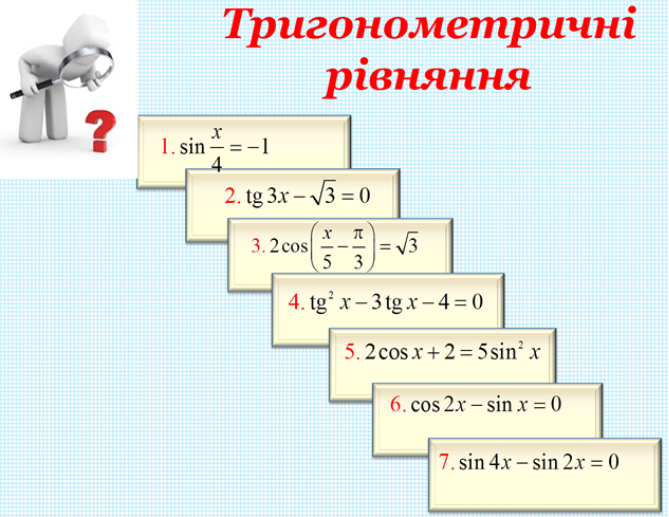
Перед вами тригонометричні рівняння.
Назвіть найпростіші
Очікувані відповіді: 1, 2, 3.
Такі рівняння ви вмієте розв’язувати за відповідними формулами. Інші рівняння не є найпростішими. Питання: Як розв’язувати ці рівняння?
Підказка (орієнтир): Як правило всі способи розв’язування тригонометричних рівнянь базуються на тому, щоб звести їх до найпростіших за допомогою заміни змінних та перетворень тригонометричних виразів. А найпростіші рівняння ви вмієте розв’язувати (є конкретні формули)
Проаналізуємо вигляд 4-ого рівняння: ![]()
Чи однакові аргументи у рівнянні? Так
Тоді наступне запитання. Чи потрібно зводити рівняння до однієї функції? Ні
Розв’язування рівняння відбувається під керівництвом вчителя.
Запис розв’язку рівняння
|
Розв’язання |
Коментар |
|
|
Помічаємо, що до складу рівняння входить лише одна функція тангенс одного аргументу х. |
|
|
Отже, зручно ввести нову змінну |
|
|
Записати рівняння, використовуючи нову змінну. |
|
|
Розв’язати отримане квадратне (алгебраїчне) рівняння |
тоді
|
Повернутися до початкової змінної (виконати обернену заміну) та розв’язати отримані найпростіші тригонометричні рівняння. Рівняння має коренів при будь-якому значенні Врахувати, що арктангенс - непарна функція.
|
|
Відповідь: |
Записати відповідь, враховуючи, що значення
|
Аналізуємо вигляд наступного рівняння: ![]()
Чи однакові аргументи у рівнянні? Так
Тоді наступне запитання Чи потрібно зводити рівняння до однієї функції? Так
Яким чином це зробити?
Йде колективне обговорення, після якого учень біля дошки розв’язує рівняння при необхідності із коментарем або за під керівництвом вчителя.
Запис розв’язку рівняння
|
Розв’язання |
Коментар |
|
|
Враховуючи, що до складу рівняння в парному степені входить тільки функція синус, виразити синус квадрат через косинус квадрат. |
|
|
Розкрити дужки і звести подібні доданки |
|
|
Ввести нову змінну |
|
|
Записати рівняння, використовуючи нову змінну. |
|
|
Розв’язати отримане квадратне (алгебраїчне) рівняння |
|
Повернутися до початкової змінної (виконати обернену заміну) та розв’язати отримані найпростіші тригонометричні рівняння., скориставшись відповідними формулами. |
|
Відповідь: |
Записати відповідь, враховуючи, що значення |
Наступні приклади будуть вам домашнім завданням.
Яким би складним не було тригонометричне рівняння, розв’язати ми його зможемо за умови дотримання певних орієнтирів (рекомендацій). Давайте їх сформулюємо і запишемо:
- Звести тригонометричні функції до одного аргументу.
- Звести тригонометричне рівняння до однієї функції
- В інших випадках переносимо всі члени рівняння в ліву частину і намагаємось розкласти на множники.
VІІ. Підведення підсумку уроку
Вчитель підводить підсумки заняття, учні підсумовують кількість набраних балів, записаних в картках самоконтролю і викладач оголошує результати.
VІІІ. Домашнє завдання
Вирішити приклади.
Висновки
Тригонометричні рівняння одна з найскладніших тем у курсі математики. Тригонометричні рівняння виникають при вирішенні завдань по планіметрії, стереометрії, астрономії, фізики і в інших областях. Тригонометричні рівняння і нерівності з року в рік зустрічаються серед завдань централізованого тестування.
На сьогоднішньому занятті Ви зуміли застосувати свої знання на практиці, обмінялися знаннями, оцінили свою діяльність на занятті та отримали можливість замислитись над підвищенням якості роботи, оцінивши свій рейтинг.
Щоб досягти успіху треба працювати, вчитися і не боятися труднощів.
Використана література
- Математика 10 клас А. Г. Мерзляк, Д. А. Номіровський, В. Б. Полонський, М. С. Якір 2018. Алгебра і початки аналізу та геометрія.
- Математика 10 клас О.С. Істер 2018. Алгебра і початки аналізу та геометрія.
- Математика 10 клас Г. П. Бевз, В. Г. Бевз 2011. Рівень стандарту.
- Мірошин В. Відбір коренів у тригонометричних рівняннях // Математика. Додаток до газети «Перше вересня».– 2006.– № 17.
- Смоляков А.Н., Севрюков П.Ф. Прийоми рішення тригонометричних рівнянь // Математика в школі. – 2004. – № 1.
- Шабашова О.В. Прийоми відбору коренів у тригонометричних рівняннях // Математика в школі. – 2004.– № 1.
Додаток 1
Картка самоконтролю
Прізвище, ім’я_______________________
Група___________ Дата_____________
|
№ п/п |
Види діяльності |
Бали |
|
1 |
Бліц-опитування ( по 1 балу) |
|
|
2 |
Відповідність «Рівняння-корені» (по 0,5 бала за кожну відповідність) |
|
|
3 |
«Чи знаєте Ви…?» (по 0,5 бала за формулу) |
|
|
4 |
Розв’язування рівнянь: |
|
|
|
№4 |
|
|
|
№5 |
|
|
|
№6 |
|
|
|
№7 |
|
|
5 |
Додаткові бали |
|
|
|
Оцінка |
|
Додаток 2
Додаток 3
![]()


про публікацію авторської розробки
Додати розробку