Ознаки зростання і спадання функцій
Про матеріал
Презентація може бути використана вчителем при поясненні нової теми на уроці, а також учнями під час самостійного опрацювання нового матеріалу в умовах дистанційного навчання. Містить завдання для усного рахунку в ігровій формі, завдання на повторення, а також приклади розв'язування вправ з даної теми. Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку



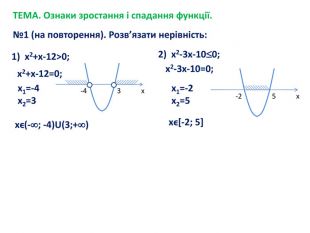
![ТЕМА. Ознаки зростання і спадання функції.№1 (на повторення). Розв’язати нерівність:1) х2+х-12>0; х2+х-12=0;х1=-4х2=3 хϵ(-; -4)U(3;+)2) х2-3х-100;х2-3х-10=0;х1=-2х2=5 хϵ[-2; 5]-43х-25х ТЕМА. Ознаки зростання і спадання функції.№1 (на повторення). Розв’язати нерівність:1) х2+х-12>0; х2+х-12=0;х1=-4х2=3 хϵ(-; -4)U(3;+)2) х2-3х-100;х2-3х-10=0;х1=-2х2=5 хϵ[-2; 5]-43х-25х](/uploads/files/878068/167405/180019_images/3.jpg)
![ТЕМА. Ознаки зростання і спадання функції.№1 (на повторення). Розв’язати нерівність:3) 6x-х20; 6x-х2=0;х1=0х2=6 хϵR4) х2-3х+8>0;х2-3х+8=0;D=(-3)2-4·8=-23, D<0 хϵ[0; 6]06х x(6-х)=0;х. Парабола не перетинає вісь Ох ТЕМА. Ознаки зростання і спадання функції.№1 (на повторення). Розв’язати нерівність:3) 6x-х20; 6x-х2=0;х1=0х2=6 хϵR4) х2-3х+8>0;х2-3х+8=0;D=(-3)2-4·8=-23, D<0 хϵ[0; 6]06х x(6-х)=0;х. Парабола не перетинає вісь Ох](/uploads/files/878068/167405/180019_images/4.jpg)
![ТЕМА. Ознаки зростання і спадання функції.№1 (на повторення). Розв’язати нерівність:5)х2-5х+4=0;х=1х=4 хϵ[1; 3)U(3;4]х2+6х+9≠0;(х+3)2 ≠0; х+3 ≠0;134х++–– ТЕМА. Ознаки зростання і спадання функції.№1 (на повторення). Розв’язати нерівність:5)х2-5х+4=0;х=1х=4 хϵ[1; 3)U(3;4]х2+6х+9≠0;(х+3)2 ≠0; х+3 ≠0;134х++––](/uploads/files/878068/167405/180019_images/5.jpg)
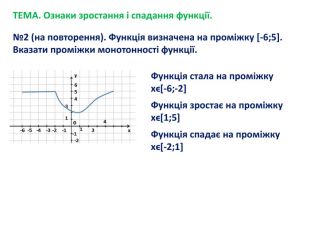
![ТЕМА. Ознаки зростання і спадання функції.№2 (на повторення). Функція визначена на проміжку [-6;5]. Вказати проміжки монотонності функції. Функція стала на проміжкухϵ[-6;-2]Функція зростає на проміжкухϵ[1;5]Функція спадає на проміжкухϵ[-2;1] ТЕМА. Ознаки зростання і спадання функції.№2 (на повторення). Функція визначена на проміжку [-6;5]. Вказати проміжки монотонності функції. Функція стала на проміжкухϵ[-6;-2]Функція зростає на проміжкухϵ[1;5]Функція спадає на проміжкухϵ[-2;1]](/uploads/files/878068/167405/180019_images/6.jpg)


![ТЕМА. Ознаки зростання і спадання функції.№3. Вказати проміжки монотонності функції:1) f(x)= х3-3х2+2;D(f)=R;f’(x)= 0;f’(x)= 3х2-6х;3х2-6х=0;3х(x-2)=0;х=0, x=2 – критичні точки;+–02х+Функція зростає на проміжку хϵ(-;0]U[2;+)Функція спадає на проміжку хϵ[0;2] ТЕМА. Ознаки зростання і спадання функції.№3. Вказати проміжки монотонності функції:1) f(x)= х3-3х2+2;D(f)=R;f’(x)= 0;f’(x)= 3х2-6х;3х2-6х=0;3х(x-2)=0;х=0, x=2 – критичні точки;+–02х+Функція зростає на проміжку хϵ(-;0]U[2;+)Функція спадає на проміжку хϵ[0;2]](/uploads/files/878068/167405/180019_images/9.jpg)
![ТЕМА. Ознаки зростання і спадання функції.№3. Вказати проміжки монотонності функції:2) y= 3х5-5х3+1;D(y)=R;y’= 0;y’= 15х4-15х2;15х4-15х2 =0;15х2(x2-1)=0;х=0, x=1; x=-1 – критичні точки;+–+Функція зростає на проміжку хϵ(-;-1]U[1;+)Функція спадає на проміжку хϵ[-1;1]–0-1х 1 ТЕМА. Ознаки зростання і спадання функції.№3. Вказати проміжки монотонності функції:2) y= 3х5-5х3+1;D(y)=R;y’= 0;y’= 15х4-15х2;15х4-15х2 =0;15х2(x2-1)=0;х=0, x=1; x=-1 – критичні точки;+–+Функція зростає на проміжку хϵ(-;-1]U[1;+)Функція спадає на проміжку хϵ[-1;1]–0-1х 1](/uploads/files/878068/167405/180019_images/10.jpg)
![ТЕМА. Ознаки зростання і спадання функції.№3. Вказати проміжки монотонності функції:3) D(f): x≠0;х=4, x=-4; x≠0 – критичні точки;+–+Функція зростає на проміжку хϵ(-;-4]U[4;+)Функція спадає на проміжку хϵ[-4;0)U(0;4]–0-4х 4хϵ(-;0)U(0;+) ТЕМА. Ознаки зростання і спадання функції.№3. Вказати проміжки монотонності функції:3) D(f): x≠0;х=4, x=-4; x≠0 – критичні точки;+–+Функція зростає на проміжку хϵ(-;-4]U[4;+)Функція спадає на проміжку хϵ[-4;0)U(0;4]–0-4х 4хϵ(-;0)U(0;+)](/uploads/files/878068/167405/180019_images/11.jpg)

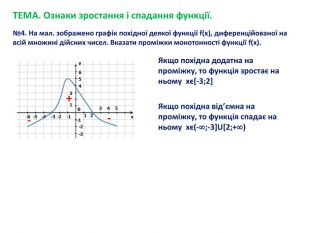
![ТЕМА. Ознаки зростання і спадання функції.№4. На мал. зображено графік похідної деякої функції f(x), диференційованої на всій множині дійсних чисел. Вказати проміжки монотонності функції f(x). Якщо похідна додатна на проміжку, то функція зростає на ньому хϵ[-3;2]+--Якщо похідна від’ємна на проміжку, то функція спадає на ньому хϵ(-;-3]U[2;+) ТЕМА. Ознаки зростання і спадання функції.№4. На мал. зображено графік похідної деякої функції f(x), диференційованої на всій множині дійсних чисел. Вказати проміжки монотонності функції f(x). Якщо похідна додатна на проміжку, то функція зростає на ньому хϵ[-3;2]+--Якщо похідна від’ємна на проміжку, то функція спадає на ньому хϵ(-;-3]U[2;+)](/uploads/files/878068/167405/180019_images/13.jpg)