МЕТОДИЧНА РОЗРОБКА «Види аксонометричних проекцій»

МЕТОДИЧНА РОЗРОБКА
«Види аксонометричних проекцій»

Розробив:  Бурикін М.С.

ПЛАН УРОКУ

Тема уроку: Види аксонометричних проекцій

Мета уроку: - сприяти формуванню в учнів знань про умови, що впливають на побудови наочних зображень предметів; навчити виконувати і читати креслення предметів; виховувати самостійність, відповідальне ставлення до роботи.

Тип уроку: формування вмінь і навичок; розв’язування графічних задач.

Форми організації уроку: фронтальне та індивідуальне опитування, бесіда з елементами пояснення, спостереження, демонстрація, виконання графічних побудов, творче конструювання нових геометричних образів.

Обладнання: креслярські інструменти, об’ємні предмети,  роздатковий матеріал, картки із різнорівневими завданнями, ПК.

Хід уроку

І. Організаційна частина

- призначення чергових, перевірка присутніх.

ІІ. Актуалізація опорних знань та життєвого досвіду.

• Аналіз графічних робіт попереднього уроку. Виставлення оцінок.
• Виконання індивідуального завдання учнями, що потребують відпрацювання креслярського шрифту (за картками).
• Перевірка д/з – індивідуальне усне опитування

Фронтальне опитування учнів.

ІІІ. Мотивація навчальної діяльності.

Повідомлення теми, завдань уроку.

ІV. Формування вмінь і навичок; розв’язування графічних задач (конспект уроку)

• Основні поняття, визначення, класифікація
•   Утворення аксонометричного зображення прямокутним проеціюванням
• Побудова аксонометричних проекцій кіл
• Побудова кола в ізометрії

VІ. Заключний етап уроку

1.  Закріплення матеріалу

1. Що називають аксонометричною проекцією?

2. У чому різниця між фронтальною симетричною та ізометричною проекціями?

2. Підведення підсумків уроку. Мотивація оцінок, виставлення їх до журналу та щоденників.

3. Домашнє завдання

ПЛАН-КОНСПЕКТ

ТЕМА: ВИДИ АКСОНОМЕТРИЧНИХ ПРОЕКЦІЙ

Основні поняття, визначення, класифікація

Термін  «аксонометрія» - ( грец. вісь і … метрія ) – означає вимірювання по осях.

Аксонометрична проекція – це проекція деталі на осях Х,Y, Z. Згідно з ГОСТ 2.317.69, визначено п’ять видів аксонометричних проекцій.  На  рис.1 зображено їх структуру.

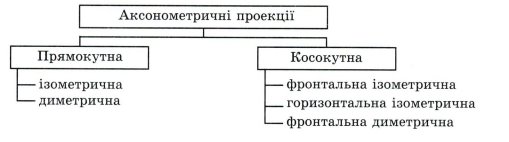
Рис. 1

 Залежно від положення координатних осей, а отже, і самого предмета відносно площини, утворюються різні аксо метричні проекції. Розглянемо ті з них, які використовують найчастіше.

  Утворення аксо метричного зображення косокутним проеціюванням

 Преміювання здійснюють паралельними проме6нями під гострим кутом (меншим за 90°) до площини аксонометричних проекцій. На одержаній аксонометричній проекції передній бік предмета зображають в натуральну величину, а лівий і верхній – дещо спотворено. Утворену косокутним проеціюванням аксонометричну проекцію називають фронтально симетричною проекцією.

  Утворення аксонометричного зображення прямокутним проеціюванням

 Проеціювання здійснюють паралельними променями, спрямованими перпендикулярно до площини аксонометричних проекцій. На одержаній аксонометричній проекції видно три боки предмета, але з деяким спотворенням. Коефіцієнти за аксонометричними осями однакові й дорівнюють 0,82. утворену прямокутним проеціюванням аксонометричну проекцію називають ізометричною.

 Осі аксо метричних проекцій. Для побудови аксо метричних проекцій розміри зображень відкладають уздовж аксометрих осей x, у і z. Тому побудову аксонометричної проекції починають з проведення аксо метричних осей.

  Осі косокутної фронтальної симетричної проекції розміщують, як показано на рис. 60, а: вісь х – горизонтально, вісь z – вертикально , вісь у – під кутом 45° до горизонтальної лінії. Осі виходять з однієї точки О – початку аксо метричних осей. Кут 45° будують за допомогою рівнобедреного косинця (рис. 2,а).

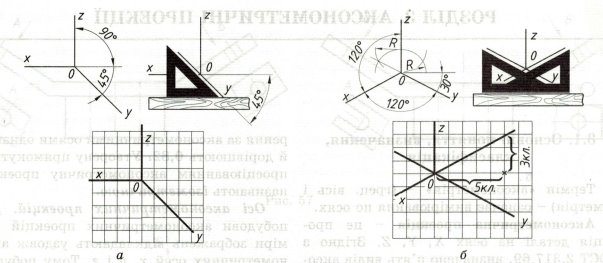
Рис.2

 Для побудови зображення у косокутній фронтальній симетричній проекції вздовж осей х і z ( і паралельно до них ) відкладають натуральні розміри фігури, а вздовж осі у – її розміри зменшені вдвічі. Звідси й походить назва «димерія», що по-грецьки означає «подвійні виміри».

 Положення осей ізометричної проекції   зображено на рис. 60, б: вісь z проводять вертикально, а осі х і у – під кутом 30° до горизонтальної лінії (120° між осями) за допомогою косинця з кутами 30°, 60° і 90° (рис. 2, б).

 Для побудови зображення в ізометричній проекції вздовж осей х, у і z (і паралельно до них) відкладають натуральні розміри предмета. Звідси і походить назва «ізометрія», що з грецької перекладається як «рівні виміри».

 Виконаємо у двох розглянутих вище видах проекцій аксонометрію деталі, креслення якої в трьох проекціях зображене на рис. 3.

1. Проведемо осі симетрії. Накреслимо фронтальну проекцію деталі на площині осей х і z (рис. 3,а).
2. З вершин отриманої фігури паралельно осі у проведемо ребра, на яких відкладемо відстань, що дорівнює товщині деталі. (рис.3,б), пам’ятаючи, що на прямокутній диметричній проекції товщину деталі відкладають удвічі меншою.
3. З’єднаємо крайні точки, дотримуючись правила, що протилежні сторони паралельні між собою (рис. 3,в).
4. Витремо зайві лінії, наведемо контури деталі і нанесемо розміри (рис.3, г) .

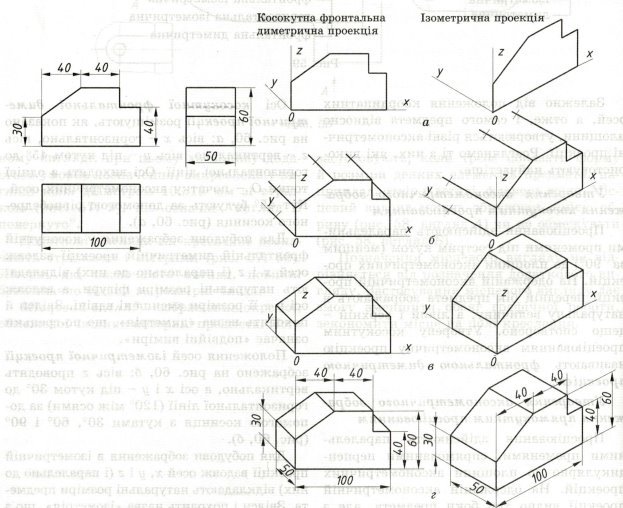
Рис. 3

Побудова аксонометричних проекцій кіл

На рис. 4, а зображена косокутна фронтальна симетрична проекція куба з колами, вписаними в його грані. Кола. Вписані на граях куб в ізометричній проекції, зображені на рис. 4, б. У цьому випадку квадрат в ізометрії перетворюється на ромб,  а коло – в еліпс.

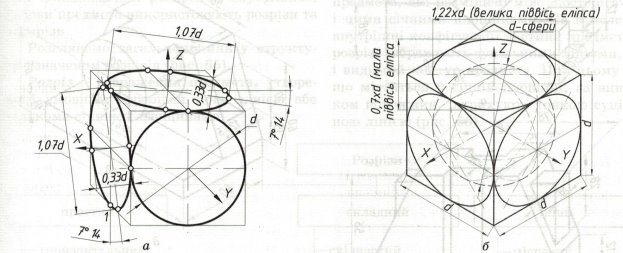
Рис. 4

Побудова кола в ізометрії

1. Будують ромб зі стороною, що дорівнює діаметру кола (рис. 5). Для цього через точку О проводять ізометричні осі х і у і на них з точки О відкладають відрізки, що дорівнюють радіусу кола. Через точки а, b, c, і d проводять прямі, паралельні осям, отримують ромб.

2. Вписують в ромб овал. Для цього радіусом R=Ad=Ac=Ba=Bb з вершин, що лежать навпроти великої діагоналі до середини протилежної сторони, описують дуги.

3. З вершин, що лежать навпроти великої діагоналі А, В проводять відрізки до середини протилежної сторони. На перетині цих відрізків і великої діагоналі утворились точки С і D. Далі проводимо малі дуги радіусом R₁=Ca=Cd=Db=Dc.

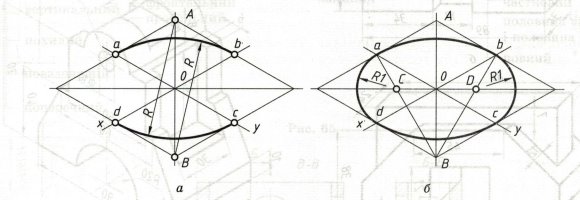
Рис. 5