Методична розробка "Використання інтерактивних технологій на уроках математики в 6 класі"
Тема: Подільність натуральних чисел.
Мікрофон.
1. Яке число називають дільником даного натурального числа а ?
2. Яке натуральне число називають кратним числу а ?
3. Ознака подільності на 2?
4. Ознака подільності на 5?
5. Ознака подільності на 10?
6. Які числа називають парними?
7. Які числа називають непарними?
8. Ознака подільності на 9 ?
9. На 3?
Мікрофон.
1. Які числа називають простими?
2. Скільки існує простих чисел?
3. Які числа називаються складними?
4. Яке найменше просте число?
5. Чому число 1 не є ані простим, ані складеним?
6. Чи є серед простих чисел парні?
7. Які числа завжди є дільниками певного числа?
8. Якими цифрами не може закінчуватися жодне з простих чисел?
9. Чи може бути простим числом сума двох простих чисел?
10. Назвіть число, що не є дільником жодного натурального числа.
Мікрофон.
1. Назвіть число, що є дільником будь-якого натурального
числа
2. Чи правильно, що кожне парне число є складеним?
3. Чи є серед простих чисел число, яке ділиться на 3? На 9? На 5?
4. Задумане просте число, наступне за ним число також є простим. Назвіть задумане число.
5. Чи вірно, що, якщо число ділиться на 2 і на 5, то воно ділиться і на 10?
6. Якщо число ділиться на 3, то воно ділиться і на 9?
7. Яке просте число є дільником всіх парних чисел?
8. Що означає розкласти натуральне число на прості множники?
9. Що таке НСД (а;в)? 10.Що таке НСК (а;в)?
11. Які числа називаються взаємно простими?
Мозковий штурм»
1. Серед чисел 385; 84; 209; 300; 616; 925; 4300; 709 назви ті, що діляться на 2; на 5; на 10.
2. Які з чисел 817; 724; 511; 900; 1002; 2005; 478; 376 є
парними?
3. Назви всі дільники чисел 24.
4. Назви всі двоцифрові числа, які кратні числу 21.
5. Які з чисел 84; 47; 306; 2001; 111; 9081 діляться на 3? На 9?
6. Яку цифру потрібно підставити замість *, щоб отримати число, яке на 3? на 9?
7. Назви всі прості числа, що більші за 4 і менші від 20.
8. Чи є взаємно простими числа: 3 і 7; 6 і 8; 5 і 11 ?
9. Серед чисел 3; 8; 15; і 20 знайди всі пари взаємно простих чисел.
Закінчити речення:
1. Кратним натуральному числу а називають натуральне число, яке ….
2. На 10 діляться всі натуральні числа, ….
3. На 5 діляться всі натуральні числа, ….
4. На 2 діляться всі натуральні числа, ….
5. Усі натуральні числа, які діляться на 2,….
6. На 9 діляться всі натуральні числа,…
7. Натуральне число називають простим, якщо….
8. Натуральне число називають складеним, якщо….
9. Найменше просте число - …. Найбільшого простого числа….
10. Два натуральних числа, найбільший спільний дільник який дорівнює 1, називають….
11. Найменшими спільним кратним кількох натуральних чисел називають найменше натуральне число,….
Знайди і виправ помилку
1. Числа, що закінчуються цифрою 1; 3; 5; 7 або 9, називаються парними.
2. Якщо число ділиться на 5, то воно обов’язково ділиться і на 10.
3. Якщо натуральне число ділиться на 3, то воно ділиться і на 9.
4. Число 28 є кратним числа 3 і 7.
5. 1 – найменше просте число.
6. 8121 – просте число.
7. Числа 9 і 27 – взаємно прості.
8. НСД ( 7 і 9) = 63
НСК ( 7 і 9) =1
Чи правильно, що ….
( Якщо твердження правильне, учні піднімають зелену картку, а якщо ні – червону)
1. Всі парні числа діляться на 2.
2. 1- найменше просте число.
3. Якщо натуральне число ділиться на 10, то воно ділиться на 5 і на 2.
4. Якщо натуральне число ділиться на 9, то воно обов’язково ділиться на 3.
5. Числа 1; 2; 3; 5; 7; 11; 17 – це всі прості числа менші 20.
6. Числа 5 і 13 взаємно прості числа.
7. Число 23 є кратним числу 3.
8. Число 7 є дільником числа 49.
9. Існує два послідовних натуральних числа, кожне з них є простим.
10. Існує три послідовних натуральних числа, кожне з яких є простим.
Робота в парах.
1. Поставте замість зірочки таку цифру, щоб отримане число ділилося на 9; 235*; 47*2; *711.
2. Відновіть цифри в наведених числах, про які відомо, що вони діляться на 3 (вкажіть всі можливі варіанти): 35*, 1*2, *71.
3. Запишіть п’ять двоцифрових чисел, які діляться і на 2, і на 3. На яке ще число діляться всі ці числа?
4. Із цифр 3;4;5 і 6 складіть усі трицифрові числа, що діляться і на 3, і на 5.
Робота в парах
1. Доведіть, що числа 145107; 9225; 41146 є складними.
2. Поставте замість * таку цифру, щоб отримане число було складеним: *137; 1*32; 71*75.
3. Запишіть
а)усі прості числа, більші від 15 і менше за 30.
б)усі складені числа, більші від 34 і менші від 42.
Робота в парах.
1. Серед запропонованих пар чисел виберіть пари взаємно простих чисел:
а) 14 ф 70; б) 17 і 43; в) 28 і 52.
2. Складіть усі пари взаємно простих чисел із чисел 12; 21 і
25.
3. Запишіть усі неправильні дроби з чисельником 27, у яких чисельник і знаменник – взаємно прості числа.
4. Між дітьми поділили порівну 155 цукерок і 62 печива. Скільки дітей отримали солодощі?
Робота в парах.
1. Знайдіть НСК знаменників дробів.
а) 
і 
; б) 
і 
.
2. Знайдіть НСК
а) перших чотирьох натуральних чисел.
б) перших трьох простих чисел.
3. Замініть * цифрами:
а= 2·2·2·3·3·5; в= 2·2·3·7; с= 2·2·0*·*·7·*;
Якщо НСК (а,в,с) = 2·2·2·3·3·5·7·7·11
Робота в групах.
Середній рівень:
1. Які з чисел 4866; 3035; 7160; 50047; 70307; 6102; 2784 діляться:
1) на 2; 2) на 5; 3) на 10; 4) на 3; 5)на 9?
2. Напишіть прості числа для яких справджується нерівність
63< ۬ ۬ ۬ <Х25
3.Знайдіть значення НСД (12;18) і НСК (12;18)
Достатній рівень:
1. Знайдіть значення числового виразу 29·31+1966:14² й розкладіть отримане число на прості множники.
2. Доведіть, що числа
а) 266 і 285 не є взаємно простими
б) 301 і 585 є взаємно простими.
3. Знайдіть НСД (28; 84; 98).
Високий рівень.
1. Замініть * такими однаковими цифрами, щоб дані числа були взаємно простими. Вкажіть усі можливі розв’язки. 1** і *4*; *3* і 6**
2. Прямокутний паралелепіпед у якого довжина 35 см, ширина 14 см і висота 21 см, розрізали на однакові великі кубики. Скільки отримали кубиків
Тема: Звичайні дроби
«Мікрофон»
1. Сформулюйте основну властивість дробу.
2. Що означає скоротний дріб?
3. Як звести дріб до НСЗ?
4. Як додати ( відняти) два звичайних дроби?
5. Які дроби називаються нескоротними?
«Мікрофон»
1. Як перемножити два звичайні дроби?
2. Як помножити натуральне число на звичайні дріб?
3. Як перемножити мішані числа?
4. Як знайти дріб від числа?
5. Як знайти відсотки від числа?
«Мікрофон»
1. Які дроби називаються взаємно оберненими?
2. Сформулюйте правило ділення звичайних дробів.
3. Як розділити дріб на натуральне число?
4. Як розділити натуральне число на дріб?
5. Як знайти число за дробом?
6. Як знайти число, якщо відомі його відсотки?
7. Як звичайний дріб перетворити на десятковий?
8. Що таке нескінченний періодичний дріб?
«Мозковий штурм»
1. Прочитайте дроби: 79; 38 ;;55
Які з них правильні, а які неправильні? 2. Виділіть цілу частину: 
; 
; 
; 
3. Замініть дріб 
натуральним числом.
4. Порівняйте дроби 3
; 5 ; 6 з одиницею.
5. 
Обґрунтуйте рівності 1 = 3 ; 2 = 8 . 6. Назвіть кілька дробів, які дорівнюють дробу: 3 ; 2 ; 1 .
7 5 11
7. Подайте число 3 у вигляді дробу зі знаменником 5;6.
«Мозковий штурм»
1. Яку частину прямого кута становлять 10º, 15º, 30º, 45º?
2. Яку частину розгорнутого кута становлять 30º, 45º, 60º,
90º
3. Яку частину доби становлять 3 години, 6 годин, 12
годин?
4. 
Яку частину години становлять 30 хв; 45 хв; 15 хв; 20 хв? 5. Скоротити дроби : 15; 3 ; 6 ; 14.
90 18 42 35
Мозковий штурм»
1. Знайдіть НСЗ дробів: 3 і 1 ; 
і ; 1 і .
7 14 3 5 7 14
2. Зведіть до НСЗ дроби: 1 і 1; 2 і 1; 3
і 1.
2 7 3 6 4 5
3. 
Порівняйте дроби: 10
і 8 ; 9 і 9 ; 4 і 1; 7 і 1; 2 і ; 5 і
21 21 19 22 5 3
.
4. Розташуйте в порядку спадання дроби:16; 1 ; 9 ; 14
; 5 ;
19 19 19 19 19
18 11
; .
19 19
«Мозковий штурм» 1. Виконайте дію: 101 +31.
2 2
2. Знайдіть різницю: 3 7 - 22.
10 5
3. 
Знайдіть значення виразу: 2 1 + 8 .
15 45
4. Розв’яжіть рівняння: Х + 2 
=5 5. Знайдіть значення виразу Х-3
, якщо Х=6
6. Виконайте дію: 4
– 2,2.
«Мозковий штурм»
1. Знайдіть зайвий дріб: 3; 13; 5; 2.
7 16 4 3
2. Перетворіть на неправильний дріб: 15; 3 2 ; 5.
7 13
3. 
Обчисліть: 3·
; 16·
; 0·1
; 1· 31; 11·2; 4 · 3; 3 · 7. 4. Подайте у вигляді добутку двох дробів число ; 8 .
9 21
5. Доведіть, що: 
і 6 та 0,3 і 3
– взаємно обернені числа.
«Мозковий штурм»
1. Знайдіть обернені числа до даних 1; 3; 5; 0,3; 21.
2 7
2. 
Виконайте дії: 
÷ 
; 
÷ 0,25; 
÷ 1; 
÷ 1; 1 ÷ ; 1÷ 
; 0 ÷ 1; 1 ÷ 3; ÷ 7; 6 ÷ 2 .
5 217 17
3. 
Чи є можливим ділення: ÷ 1; 0 ÷ ; 1 ÷ 8 ; 7 ÷ 0 ?
13 15
4. 
Серед виразів: ; 5÷8; 13÷3; 5; 8; 3÷13 знайдіть рівні.
8 5
Продовж речення:
1. Щоб скоротити дріб, треба…
2. Щоб додати (відняти) два дроби з різними знаменниками, треба….
3. Щоб порівняти два дроби з різними знаменниками, треба….
4. Щоб помножити два звичайних дроби, треба….
5. Щоб знайти число, обернене даною, треба…
6. Щоб поділити два звичайних дроби, треба…
7. Щоб знайти дріб від числа, треба…
8. Щоб знайти число за його дробом, треба…
9. Щоб перетворити звичайний дріб у десятковий, треба… Чи правильно, що:
1. 
1 = 5 ; 8 = 2 ; 3 м = дм ?
4 20 12 3 4
2. 
0,8 і ; 0,2 і 5; 3 і 1; 21 і 7 - взаємно оберненні?
3 7 15
3. 2 + 5 = 7 = 1 ?
7 7 14 2
4. 3 − 12 = 22 ?
5 5
Продовж речення:
1. Скоротити дріб – означає….
2. Дріб називають нескоротним, якщо його чисельник і знаменник ….
3. Якщо скоротити дріб на НСД чисельника і знаменника, то отримаємо….
4. Усі правильні нескоротні дроби зі знаменником 12 мають вигляд….
5. Усі неправильні нескоротні дроби із чисельником 15 мають вигляд …
Знайди помилки:
1. 0,5 і 
; 7 і 
; 0,3 і 3 – взаємно обернені числа. 2.1 + 1 = 2.
2 3 5
3. 6 - 2 = 4 = 1
7 3 4
4. 
3 · = 1; 0 · 9 = 9 ;
13 13
5. 
÷ 7 = = 1 ÷ 0 = 0 1÷ 8 = 8
11 11
Робота в групах:
1. С
1. Помножте чисельник і знаменник кожного з дробів 
; 3 ; 4 на 3 і напишіть відповідні рівності.
5 9
2. 
Розділіть чисельник і знаменник кожного з дробів 15; 60;
35 80
на 5 і запишіть відповіді рівності.
3. Запишіть три дроби, які дорівнюють 
. 4. Замініть х таким числом, щоб справджувалась рівність:
3 6 х 16 1 9 56 х
= ; = ; = ; = .
7 х 5 20 5 х 98 14
2. Д
1. Запишіть: число 2 у вигляду дробу, знаменник якого дорівнює 22. Число 6 у вигляді дробу, знаменник якого дорівнює 666.
2. Розв’яжіть рівняння.
Х = 4 ; х = 28; 5х = 40.
33 11 7 44 6 48
3.В
1. Назвіть усі дроби, які більші за 
і чисельник яких дорівнює 1.
2. Скоротним чи не скоротним дробом є значення виразу:
1) 
2) 
.
3. Розв’яжіть рівняння:
18 32021 7 21
= ; = 
; = 
; = .
24 х−6х−311х х+4 60
Робота в групах
С 1. Серед дробів 
; 
; 
; 0,8; 
знайдіть рівні.
2.Виконайте дії та скоротіть результат:
а) 313 + 617 б) 12 − 7
45 45
3.Знайдіть х, якщо х = 7 +
6 12
Д 1. Скоротіть дріб: 
2.Напишіть три доби, що дорівнюють 
.
3.Визначте, яку частинку року становлять 8 місяців.
Запишіть відповідь у вигляді нескоротного дробу.
В 1.Скоротіть дріб: а) 
; б) 0,2432 2.Знайдіть х, якщо 5
х−8 = 4 − 2
5 Робота в парах:
С Порівняйте дроби:
3 і 2; 2і 3 ; і ; 7 і 3; 3 і 1
8 3 5 710 4 5 6
Д Порівняйте дроби; 
і 
; 
і 
; 0,3 і 
; 
і 0,85.
В Розташуйте дроби в порядку спадання: ; ; 3 ; 5 ; 13 ; 1.
4 12 18 2
Робота в парах: С Розв’яжіть рівняння х + = ; х - 1 = 2 ; х + 4 = 5; 5 − х = ; х + =
10 15 9 6 9
Д Розв’яжіть рівняння: х – 0,7 = 1 ; 1 − х = 0,45; − х = 0,375; х + =
5 2
; х + 
= 
.
В Розв’яжіть рівняння:
+ ( х − 
) = 
( + х ) - 2 = 13
3 18
Робота в групах:
С 1.Знайдіть суму:
1
+ 
; 8 
+ 4 
; 2 
+ 1 
Д 1.Виконайте дії:
+ 1− ; 2+ 1+ + ; 19 − 5 − 5.
6 7
2.Розв´яжіть рівняння:
1 
− х = 
; х + 
= 1 
.
В 1.Знайдіть значення виразу:
+ ( 3 + 1 ) +
8 12
2.Розв´яжіть рівняння:
3
− ( 5 
− х ) = 1 
8
− х = 
+ 2 
Робота в групах:
С 1.Обчисліть:
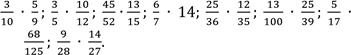
2.Знайдіть значення виразу:
( 
)²; ( 
)³
Д 1.Обчисліть:
;
2.Знайдіть значення виразу:
;
В 1.Обчисліть:
2.Що є більшим – сума чисел 
і 
чи їхній добуток?
Робота в парах
С 1.Обчисліть:
2.Розв´яжіть рівняння:
Д 1.Обчисліть:
2.Розв’яжіть рівняння:
Х : 1
= 2 
В 1.Знайдіть значення виразу:
;
Робота в групах:
С 1.Виконайте ділення:
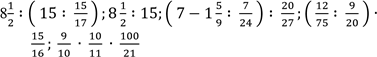
2.Розв´яжіть рівняння:
Д 1.Виконайте дії:
;
.
2.Розв´яжіть рівняння:
.
х + 
х − 
х = 
х + 
= 
В 1.Знайдіть значення виразу:
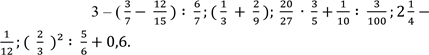
2.Розв´яжіть рівняння:
( х – 4,5 ) · 2
= 2,4.
Робота в групах:
С 1. Запишіть у вигляді десяткового дробу:
3 5 ; 1 7 ; 5 ; ;
16 10
3. Виконайте дії в десяткових, а потім у звичайних дробах: 3,4 - 
2 ; 3 + 1,03;0,35 + 2 .
25 40
Д 1. Запишіть у вигляді десяткового дробу: 4 ; 9 ; 126 ; 19 ; .
125 18 125 32
2.Знайдіть середнє арифметичне чисел:
5,25 і 2
; 8 
і 4,83; 3 
; 1 
і 4,15.
В 1.Знайдіть значення виразу:
( 1,2 : 36 + : 0,25 -
.
Робота в групах:
С. 1. Перетворіть дріб на нескінченний десятковий і вкажіть його період: 
; 
; 
; 
2.Знайдіть десяткове наближення до сотні дробу:
17 13 19 1
; ; ; 8
24 23 26 12
Д 1. Порівняйте дроби,записавши попередньо звичайні дроби у вигляді десяткових:
1,6 і 1
; 
і 
; 
і 0,58 (4).
2
і 2,4 (25); 3,14 і 
2.Перетворіть звичайні дроби на десяткові, округліть їх до сотих і виконайте дії:
8,58 + 4
− 1 
; 8 
− 5,82 − 2 
В 1. Порівняйте: 
і 0,9 (4)
2.Перетворіть звичайні дроби на десяткові, округліть їх до сотих і виконайте дії:
6
+ 2,96 − 1 
8
− 5,82 − 2 
4.Розв’яжіть рівняння й округліть отриманий корінь до тисячних:
4 ( 14 х – 3 ) = 1
Мозковий штурм
1. Порівняйте:
6,4 і 6,43; 1,28 і 1,3; 0,3 і 0,0007; 0,028 і 0,1; 5,3 і 5,(3) 2. Округліть дроби: 0,6372; 2,2981; 6,7777; 4,7676:
а) до десятих; б) до сотих; в) до одиниць.
3. Прочитайте числа:
0,(5); 1,3 (2); 0,68(8); 2,(89).
4.У вигляді кінцевого чи нескінченного десяткового дробу можна записати дріб:
; 
; 
; 
; 
Тема: Відношення і пропозиції.
« Мікрофон»
1. Що називають відношенням двох чисел?
2. Що показує відношення двох чисел?
3. Що таке пропорція?
4. Як записати пропорцію в загальному вигляді?
5. Як називаються члени пропорції?
6. Сформуйте основну властивість пропорції.
7. Як знайти невідомий крайній член пропорції?
8. Як можна перевірити чи пропорція вірна?
« Мікрофон»
1. Що таке відсоткове відношення двох чисел?
2. Сформуйте правило знаходження відсоткового відношення двох величин.
3. Які дві величини називають прямо пропорційними?
4. Чим характерне відношення відповідних значень прямо пропорційних величин?
5. Наведіть приклади величин, які не є прямо пропорційними. Мозковий штурм.
1. Знайдіть відношення:
12 до 3; 10 до 50; 17 до 3.
Що показує кожне з цих відношень?
2. Назвіть два числа, відношення яких дорівнює:
а) 5; б) 
; в) 
3. Чи правильно, що відношення 25 до 100 дорівнює 4?
4. Чи є пропорцією рівність:
а)15: 45 = 6 : 18 ; б)4 : 2 = 5 – 3; в) 12 : 3 = 1 + 3?
5. Чи є правильною пропорція:
а) 4 : 3 = 15 : 12; б) 15 : 55 = 6 : 22 ?
6. Визначте невідомий член пропорції:
7
а)х : 8 = 5 : 4 ; б) 9 : 2 = х : 3 ; в) = . х
Як його знайти?
Мозковий штурм.
1. Перевірте, чи є правильною пропорція 
.
2. Напишіть пропорцію, у якій середні члени 3 і 8, а крайні – 4 і 6.
3. 
Використовуючи пропорцію 3 : 21 = 2 : 14, запишіть ще три пропорції. 4. Відомо, що х = . Як відноситься х до у ?
15
Мозковий штурм
1. Скільки відсотків становить число 20 від 50 ?
2. Скільки відсотків від числа становить його чверть?
П’ята частина? Половина?
3. Знайдіть 20% від 40 грн.
4. Виразіть десятковим дробом відсотки: 8% ; 12%; 0,8%; 1,3%; 128%.
5. Виразіть у відсотках числа: 0,32; 0,7; 
; 
; 
; 2; 4.
Продовж речення:
1. Пропорцією називається . . . . .
2. Якщо пропорція правильна, то . . . . .
3. Щоб знайти середній член пропорції потрібно . . . .
4. Щоб знайти середній член пропорції потрібно….
5. Якщо зі збільшенням однієї величини в кілька разів друга величина збільшується в стільки ж разів, то такі величини називаються….
Закінчіть речення.
1. Усі точки кола рівновіддалені від .. .. .
2. Відрізок, який сполучає дві точки кола, називається . .. .
.
3. Відрізок, який сполучає центр кола з точкою на колі, називається . . . .
4. Хорда, що проходить через центр кола, називається . . .
5. Діаметр – це найбільша . . . . .
6. Діаметр дорівнює . . . . .
Робота в групах
1. С Запишіть пропорцію, у якій кожне з відношень дорівнює 5.
2. Із яких відношень: 0,6 : 5; 4,2 : 7; 
6,25 можна скласти правильну пропорцію?
3. Користуючись основною властивістю пропорції, перевірте чи є правильною пропорція:
а) 
4
б) 
= 
; в) 1,5 = 2,7
2. Д Розв’яжіть рівняння:
а) х : 1
б) 5
−У =
4
в)1,2 : 0,5х = 1,8 : 1
3.В 1. Дано пропорцію 9
Знайдіть добуток ху, укажіть дві пари можливих значень середніх членів цієї пропорції.
2.Розв´яжіть рівняння:
5 = 10
0,6 0,02х−3
Робота в групах
1. С Розв’яжіть рівняння:
х 9 5 а 1 х 1
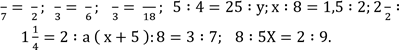
2. Д Для кожної з рівностей
2 · 20 = 5 · 8; 12 · а = 6 · 7
х · у = u · у запишіть по дві пропорції.
2.Запишіть дві пропорції, добутки крайніх членів яких дорівнює 12.
3.Запишіть дві пропорції, добутки середніх членів яких дорівнює 8.
3. В Знайдіть такі значення х і у, щоб кожна з рівностей х = 2 і у = була правильною. у 3 24
Робота в групах:
1. С Знайдіть відношення 8 до 24 А) 3; Б) 6; В) 
; Г) 12.
2. Укажіть приклад пропорції:
А) 5: х = 20; Б) 7 : 2 = 14 : 4; В) 8 : 2; Г) 
3. Укажіть правильну пропорцію
А) 
;
В)
2. Д 1. Складіть правильну пропорцію з чисел: 0,2; 1,6; 0,72;
0,09
2.Розв´яжіть рівняння:
= 
В Складіть із чисел 3; 5; 6; 10 вісім правильних пропорцій.
Ділова гра (робота в групах):
Вчитель пропонує учням об’єднатися в групи для ділової гри. Кожна група одержує задачу економічного характеру, розв’язує її та пропонує розв’язання на обговорення іншим групам. Кожна з груп дає рецензію на відповідь групи, яка відповідала.
Задачі для роботи «економістів».
1. Щоб врахувати інфляцію, що становила 5%, підприємець підняв ціну на кожну одиницю товару з 1250 грн до 1290 грн. Чи правильно зроблено розрахунок? ( Відповідь: ні).
2. Вкладник вніс до банку 600 грн під 12% річних, через рік річна ставка зросла до 15%. Скільки грошей вкладник одержить через два роки? ( Відповідь: 772,8 грн).
3. Ціну на товар, який коштував 1000 грн, зменшили на 20%. На скільки відсотків треба підняти нову ціну, щоб одержати початкову? (Відповідь: на 25%).
4. Ціну на товар, який коштував 1500 грн, спочатку зменшили на 20%, а потім нову ціну збільшили на 20%. Якою є ціна товару після двох переоцінок? ( Відповідь: 1440 грн)
5. До магазину надійшли книжки за ціною 10 грн 50 коп. Націнка магазину становить 20%. Під час оптової закупівлі робиться знижка 5%. Якою буде ціна книжки при оптовій закупівлі? (Відповідь: 11 грн. 97 коп.).
Картка для групи:
1. Чи пропорційні числа 1,2; 1,4; 2,6; числам 3; 3,5; 6,5.
2. Розділіть число 2,16 на частинами, пропорційні числам
17; 6;4.
3. Поле площею 600 га розбито на чотири частини, пропорційні числам 2; 3; 7 і 8. Знайдіть площу кожної частини.
4. Відрізок АВ завдовжки 80 см поділили на частини, пропорційні числам 3,4,4і 5. Знайдіть довжини цих частин.
5. Розгорнутий кут розділили на частини, пропорційні числам 5 і 4. Знайдіть градусні міри утворених кутів.
6. Сторони одного чотирикутника 1,2; 1,4; 2,6; 2,8 дм, а сторони другого – 3; 3,5; 6,5 і 7 дм. Чи пропорційні сторони цих чотирикутників?
Тема: Раціональні числа та дії над ними.
Мікрофон
1. Які числа називаються додатними? А від’ємними?
2. Скільки існує додатних чисел? Від’ємних чисел?
3. Які числа називаються натуральними?
4. Чи є число 0 натуральним числом?
5. Отже найменше натуральне число ..? А найбільше?
6. Назвіть перші три натуральних числа та їм протилежні
7. Назвіть найбільше двоцифрове число (натуральне), а протилежне йому?
8. Назвіть найменше трицифрове натуральне число.
9. Які числа називаються цілими?
10. Які числа називаються раціональними?
11. Чи завжди цілі числа є раціональними, а навпаки?
Мікрофон
1. Які числа називаються протилежними?
2. Чи може відстань бути від’ємною ?
3. Що називається модулем числа?
4. Чому дорівнює модуль додатного числа; від’ємного числа; нуля?
5. Що можна сказати про модулі протилежних чисел?
6. Які числа мають модуль, що дорівнює 9?
7. Як розміщуються на координатній прямій точки, що зображують нерівні числа з рівними модулями?
Мікрофон
1. На координатній прямій більше число розташоване праворуч чи ліворуч?
2. Яке число є більшим: додатне чи від’ємне ?
3. Що більше – додатне число чи 0 ?
4. Як порівняти два додатних числа?
5. Як порівняти два від’ємних числа?
Мікрофон
1. Яким числом, додатним чи від’ємним, є сума двох від’ємних чисел?
2. Сформулюйте правило додавання двох від’ємних чисел.
3. Від чого залежить знак суми чисел із різними знаками?
4. Сформулюйте правило додавання двох чисел із різними знаками.
5. Чому дорівнює сума протилежних чисел?
6. Які закони додавання ви знаєте?
7. Якою дією замінюється віднімання?
8. Як виконати дію віднімання ?
9. Коли різниця двох чисел є додатною?
10. Коли різниця двох чисел є від’ємною ?
11. Коли різниця двох чисел дорівнює нулю?
Мікрофон
1. Як скласти два від’ємних числа?
2. Як знайти суму додатного і від’ємного числа?
3. Чому дорівнює сума двох протилежних чисел?
4. Як від одного раціонального числа відняти інше?
5. Як розкрити дужки, перед якими стоїть знак «+»?
6. Як розкрити дужки, перед якими стоїть знак «-»?
Мікрофон
1. Як знайти добуток двох від’ємних чисел?
2. Як знайти добуток двох чисел із різними знаками?
3. За якої умови добуток дорівнює 0?
4. Що є більшим: добуток двох чисел з однаковими знаками чи з різними?
5. Які знаки повинні мати два числа, щоб їхній добуток був додатним числом? Від’ємним числом?
6. Що таке коефіцієнт виразу?
7. Які властивості множення ви знаєте?
8. Як поділити два від’ємних числа?
9. Як подіти два числа з різними знаками?
Мікрофон
1. Сформулюйте переставний закон множення.
2. Сформулюйте сполучний закон множення.
3. Сформулюйте розподільний закон множення.
4. Що таке коефіцієнт7
5. Які доданки називаються подібними?
6. Як звести побідні доданки?
Мікрофон
1. Що називають рівнянням?
2. Що називають коренем рівняння?
3. Сформулюйте правило переносу доданків з однієї частини рівняння в іншу.
4. Чи зміняться корені даного рівняння, якщо обидві його частини помножити або розділити на те маме число, що не дорівнює 0 ?
5. Що означає розв’язати рівняння?
Мікрофон
1. Які прямі називаються паралельними?
2. Які прямі називаються перпендикулярними?
3. Що таке прямокутна система координат ?
4. Що таке координатна площина?
5. Як називаються осі прямокутної системи координат?
6. Яка особливість точок площини, що лежать на осі абсцис?
7. Яка особливість точок площини, що лежать на осі ординат?
«Мозковий штурм»
1. Якщо Петро зайде в ліфт 13- ти поверхового будинку на 7 – му поверсі і проїде 4 поверхи, де він вийде?
2. Назвіть чотири числа:
А) які є цілими, але не натуральними
Б) які є раціональними, але не цілими
3. Назвати модуль числа: 4; -6; -5,2; 12 
; 0.
4. Назвіть три числа, які розташовані на координатній прямій
А) лівіше від числа 0,2
Б) правіше від числа -10,4
В) лівіше від числа -6, але правіше від числа -12.
5. Скільки цілих чисел розташовано на координатній прямій між числами -6,4 і 6,4?
6. Відомо, що |х|=5. Чому дорівнює |-х| ? а х?
«Мозковий штурм»
1. Яке число є меншим:
13 чи 9; 6 чи 0; -3 чи 1; -6 чи -8?
2. Яке число є більшим:
7 чи 0; -16 чи -17; -9 чи -8; -4 чи 0?
3. Порівняйте числа:
−4 
і − 3; −0,2 і − 
; −7 і − 6 
4. Яка з нерівностей є правильною:
−31 < −26,9; −8 < −4; −6,7 < −12; 6,7 < −12?
5. У якому з наведених випадків числа розташовано в порядку спадання:
А) -9,8; -7; 6; -5 Б) -9; -7; -5; 6; 8 В) 8; 6; -5; -7; -9 Г) -5; -7; 6; 8; -9?
6. Назвіть у порядку зростання цілі числа:
А) від -5 до 5 Б) від – 6 до 2 В) від – 100 до – 90;
7. Між якими послідовними цілими числами розташоване число: -4,3; 0,28; -0,65?
«Мозковий штурм»
1. Яке з чисел більше: - 48 чи -84; 0,0001 чи -100; 0 чи -2,7; -0,008 чи -0,8; −1 
чи -1,6?
2. Назвіть які небудь чотири цілих числа, які:
А) менші від 0; Б) менші від -6;
В) більші за 0; Г) більші за -6?
3. Назвіть у порядку спадання цілі числа:
А) від 0 до -10; Б) від -8 до -14; В)від 4 до -4
4. Якою, додатною чи від’ємною, буде сума чисел а і в, якщо :
1) а > 0 і в > 0 2) а < 0 і в < 0 3) а = 0 і в > 0 4) а < 0 і в = 0 5) а > 0 і в < 0 6) а < 0 і в > 0 ?
«Мозковий штурм»
1. Виконайте додавання:
−
+ (− 
) ; −5,2 + (−5,2); (−1,3) + (−0,7)
− 
+ (− ); (−30) + (−70); −0,4 + (−12)
5
2. Знайдіть значення суми:
−1 + 0,8; −0, +1; − 
+ (− 
); −3 + 1,3;
2 5 2
4,2 + (−6); −0,1 + (−1); − + ; + (−).
9 9 9
3. Назвіть п’ять найменших послідовних цілих чисел, які більші за -2,3
4. Скільки існує цілих чисел х, при яких є правильною нерівність |х| ≤ 34; |х| < 100?
5. Наведіть приклад двох чисел з різними знаками, сума яких дорівнює: 10; -6; 0; -8.
6. Наведіть приклад двох чисел з однаковими знаками, сума яких дорівнює: 3; -20; -1.
7. Сума трьох доданків дорівнює одному із них. Як пов’язані між собою два інших числа?
«Мозковий штурм»
1. Назвіть п’ять найбільших послідовних цілих чисел, які менші від 1,9.
2. Виконайте віднімання:
−2 − 1,3; 3 − 7; −2,6 − 4; 5 − 19;
0,4 − 1; 
− 
; 3— 8; 
− 1;
10 − (−4); 0 − 
; 0 − (−5 
)
3. Між якими сусідніми цілими числами лежить число:
-7,86; 0,16; -0,08; -3?
4. При яких цілих значеннях х є правильною нерівність: −2 < х ≤ 4; −3 ≤ х ≤ 1,2?
5. Назвіть три яких – небудь значеннях х, при яких є правильною нерівність:
х < 0; х > 3,7; х < −2,8
«Мозковий штурм»
1. Виконайте дії:
−1 + 
; −3 + 1 
; 2 
− 5; −1 
− 
;
1 5
− 1; −8 − 4; −2 + 1; −1 + .
6 6
2. Укажіть усі цілі значення х, при яких є правильною одночасно кожна нерівність
−4 < х ≤ 3 і − 3,7 ≤ х < 5. 3. При яких значеннях а дріб а
+6 буде правильним?
9
4. Чому дорівнює сума всіх цілих чисел які більші за -8, але менші за 6?
5. Яких значень, додатних, від ємних чи нуль, може набувати вираз – (-а)?
6. Розв’яжіть рівняння:
1 + к = −1; 16 + к = 4;
−к − 5 = 0; 11 − к = 18.
«Мозковий штурм»
1. Виконайте множення:
;
.
2. При яких цілих значеннях у є правильною нерівність:
|у| ≤ 3; |у| < 4,2; |у| ≤ 0?
3. Додатним чи від’ємним є число а, якщо:
−3а < 0; 
а < 0; −0,7 а > 0?
4. При яких цілих від’ємних значеннях х є правильною нерівність: −3х < 12?
5. Яке з чисел -2;-1;0;1 є значенням виразу
(−1)3 + (−1)4 + (−1)5 + (−1)6 + (−1)7 ?
«Мозковий штурм»
1. Обчисліть добуток:
;
2. Спростіть вираз:
0,3 ∙ 1,6ав; 0,5к ∙ 9п; 
𝜎; 
.
3. Чи є число -8 коренем рівняння: х + 15 = 7; 18 − х = 10; −7х = 56; 2х − 2 = 14?
4. При яких цілих невід’ємних значеннях х є правильною нерівність −4х > −28?
5. Порівняйте значення виразів:
3,69 ∙ (−1)60 і 3,69 ∙ (−1)75.
«Мозковий штурм»
1. Спростіть вираз:
−0,4 ∙ (−6а); 5𝛿 + 7𝛿; 6х + 2х + х; 10а − 4а; 9у + 2у − у; 30р(−0,8𝜇); −𝛽 − 4,2 + 4,2 + 3𝛽.
2. Порівняйте з нулем:
(−7)9; (−0,4)12; (−12)1; 099.
3. Квадрати двох чисел рівні. Чи обов’язково що ці числа рівні?
4. Зведіть подібні доданки:
4а − 6а; −3х + 9х; −5х + 4у − х − 10у;
−1,2а − 0,8в + 0,4а; 10р + 12п − 6р − 20п
5. Яку цифру можна поставити замість *, щоб була правильною нерівність −2 ∗ ,43 > −23,61?
6. Чому дорівнює добуток усіх цілих чисел, які більші за 10, але менші від 10?
«Мозковий штурм»
1. Знайди частку:
12 ÷ (−3); −28 ÷ (−0,7); −3,6 ÷ (−4); −2 ÷ (−0,5); −54 ÷ (−90); 0,96 ÷ (−0,012).
2. Чому дорівнює сума 1000 доданків, кожний з яких дорівнює -1?
3. Чому дорівнює добуток 1000 множників, кожен з яких дорівнює -1?
4. Назвіть число, яке протилежне до даного, і число, яке обернене до нього:
; −
; 9; −6; 4 
; −9 
.
5. Обчисліть значення виразу |х| ÷ х, якщо х =
7; −0,4; −1,9; 3 
; −9 
.
6. У якому випадку всі три дроби рівні:
1) − 
; 
і 
; 2) 
; 
і 
3) − 
; 
і 
; 4) − 
; 
; 
?
7. Чи ділиться націло на 3 значення виразу:
1014 − 1; 1010 + 5?
«Мозковий штурм»
1. Знайдіть добуток коренів рівняння (х+6)(х-1,5)=0
2. Які з наведених рівнянь не мають коренів: х = 4 = 1; х − 2 = 5 + х; |х| + 2 = 1 0х = 0; х ∙ х = х?
3. Спростіть вираз: −х ∙ (−2,4) ∙ 5у; −0,9(−а) ∙ 9в
4. Чому дорівнює сума всіх цілих чисел, які розташовані на координатній прямій між числами -72 і 70?
5. При яких цілих додатних значеннях у є правильною нерівність −0,7у > −3?
6. При яких значеннях а є правильна рівність а ÷ 5 = 5 ÷ а?
«Мозковий штурм»
1. Виконайте дії:
−0,18 + 1,8; 
; 7,5 ÷ (−1,5);
−0,18 − 1,8; 
; 
;
÷ (−
) ; −7,5 ⋅ (−4); 2,4 − (−1,6)
−0,14 ⋅ 50; − 
÷ (− 
)
2. Відомо, що серед чисел 5052; 6062; 7072; 8082; 9092 є значення виразу 3032 + 4042. яке саме?
3. Назвіть коефіцієнт виразу:
8𝛿 ⋅ 0,5; а ⋅ (−18в); 
у;
−х ⋅ 9 − (1,2); −р ⋅ (−4𝜚); −а ⋅ (−1,2в) ⋅ 5с
4. У якій чверті координатної площини знаходиться точка:
А (2;8) В(-6;-2) С(1;-2) Д(-3;-8)?
5. Які з точок А(-6;0) В(3;1) С(0;4) Д(0;9) О(0;0) F(4;0) G(1;1) належать координатній осі і якій?
6. Яку цифру можна поставити замість*, щоб число 792* ділилося націло на 6, але не ділилося на 10?
«Вірю – не вірю» (червоні і зелені карточки) 1. Чи вірно, що 0 натуральне число?
2. Чи вірно, що на координатній прямій0 стоїть між додатними і від’ємними числами?
3. Будь – яке додатне число більше від 0.
4. Будь – яке від’ємне число менше за 0.
5. Із двох від’ємних чисел більше є те, модуль якого більший.
6. Твердження, що а – невід’ємне число, можна записати у вигляді нерівності а > 0 .
7. Нерівність х ≤ 0 можна прочитати так: х – не додатне число.
8. Цілими числами, що задовольняють умову −2 ≤ а ≤ 2, є числа − 2; −1; 1; 2.
9. Натуральними числами, що задовольняють умову а ≤
4, є числа 0;1;2;3;4.
«Вірю – не вірю»
1. Число -5 можна прочитати як «число, протилежне числу 5»
2. Якщо перед дужками стоїть знак «+», то при розкритті дужок треба опустити цей знак, а всі знаки, що стоять перед доданками, змінити на протилежні.
3. Якщо перед дужками стоїть знак «-», то при розкритті дужок треба опустити цей знак, а всі знаки, що стоять перед доданками, залишити без змін.
4. Щоб від одного числа відняти інше, достатньо зменшуване скласти з числом, протилежним від’ємнику.
5. Правило віднімання можна записати так
а − в = а + (−в)
6. Щоб знайти довжину відрізка на координатній прямій, потрібно від координати його лівого кінця відняти координату правого.
«Вірю – не вірю»
1. Будь – яке натуральне число є цілим числом.
2. Будь – яке натуральне число є раціональним числом.
3. Будь – яке ціле число є натуральним числом.
4. Будь – яке ціле невід’ємне ціле число є натуральним.
5. Будь – яке ціле число є раціональним числом.
6. Якщо число не є натуральним, то воно є дробовим числом.
7. Якщо раціональне число не є дробовим, то воно є натуральним?
«Продовж речення»
1. Протилежні числа відрізняються одне від одного …
2. Для кожного числа існує тільки одне …
3. Число, протилежне додатному числу…
4. Число, протилежне від’ємному числу …
5. Число 0 протилежне …
6. Сума двох протилежних чисел …
7. Кожне натуральне число є …
8. Кожне ціле число є …
«Продовж речення»
1. Щоб додати два від’ємних числа, треба …
2. Щоб додати два числа з різними знаками, треба …
3. Щоб від числа а відняти число в, треба …
4. Щоб помножити два від’ємних числа , треба …
5. Щоб помножити два числа з різними знаками, треба …
6. Щоб поділити два від’ємних числа, треба …
7. Щоб поділити два числа з різними знаками, треба …
8. Щоб розкрити дужки перед якими стоїть знак «+», треба
…
9. Щоб розкрити дужки перед якими стоїть знак «-», треба
…
10. Щоб звести подібні доданки, треба …
«Продовж речення»
1. Якщо добуток ав є додатним, то число а і в мають … 2. Якщо добуток ав є від’ємним , то число а і в мають ...
3. Якщо добуток ав дорівнює 0, то хоча б одне із чисел а чи в …
4. Для будь – якого значення х вираз х2 набуває тільки…
5. Добуток двох від’ємних чисел має …
«Продовж речення»
1. Рівнянням називається рівність, яка містить …
2. Значення змінної, яка перетворює рівняння на правильну рівність, називається …
3. Розв’язати рівняння означає …
4. Корінь рівняння не зміниться, якщо …
А) доданок перенести з однієї частини в іншу, при цьому
…
Б) обидві частини рівняння розділити або помножити на
…
5. Під час складання рівняння до задачі потрібно:
А) позначити невідоме через …
Б) виразити відомі величини через …
В) скласти і розв’язати …
Знайди і виправ помилку
1. Число 5 розташоване на координатній прямій ліворуч від 0.
2. Невід’ємні цілі числа – це натуральні числа
3. |17|=17, а |-17|= - 17
4. −14 > −10; − 
< −0,2; − 
> − 
.
5. −5 + (−5) = 0; −5 + 5 = 10; 5 + (−5) = 0
6. дані числа розташовані в порядку зростання: 0; 1; -2; 3; -
4.
7. Обчислити:
-7+19+7=33; -28+16-16+28=0
Знайди і виправ помилку
1. Обчисліть:
-7-(-1)=-8; 12-(-16)=-4; -12+(-8)=-20;
-12-(-8)=4; -1,5-1,5=0; 4-(-11)=-7
2. Розв’яжіть рівняння:
Х+5=3; -10-х=6; 3-х=-1;
Х=5-3 х=6+(-10) х=3-1
Х=2 х=-4 х=2
3. Число – 0,8 між -1 і -2.
Знайди і виправ помилку
1. Число -8 є коренем рівняння 18-х=10
2. Обчислити:
−0,7 ∙ (−25) ∙ (−4) = −7 12,5−12,5 ∙ 5 ∙ 0,2 ∙ (−8) = −10
3. Спростити вираз:
−2 ∙ а ∙ (−1,8) = −0,36а; 8р ∙ (−0,9) = −0,72р −5а ∙ (−0,2в) = −10в; −200х ∙ 0,1у ∙ (−𝑧) = −100ху𝑧
4. Порівняйте:
(−1)5 < (−1)15; (−1)100 > (−1)2; (−1)4 < (−1)99.
«Робота в парах»
С
1. Задумано від’ємне число, модуль якого дорівнює 7. Яке число задумано?
2. Знайдіть модуль числа: -1; 17; -3,2; 7,1; 0; - 18. Запишіть відповідні рівності.
3. Знайдіть х, якщо
|х| = 9; |х| = 10,36; |х| = 0; |х| = −4
4. Знайдіть значення виразу:
а) |−14,4| − |2,3| б) | − 49| ÷ |0,7|
в) |−1| + |−1,7| г) | − 0,5| ∙ | − 0,5|
Д
1. Знайдіть значення виразу:
|−66,66|:|−33|; |−20| − |−0,9| |−0,3| · |−0,9|; |−0,09| + | − 0,1|
2. Розв’яжіть рівняння:
|х| − 18,2 = 1; |х| − 7 = 0; |х| + 3 = 0; |−х| = 7,8
В
1. Відомо, що |а| = |в|. Чи правильно, що а = в?
2. Розмістіть числа в порядку зростання їхніх модулів:
а) 4,1; −2,5; −4; −1,7; 6,07
б) − 1,2; 2,1; 0; −0,9; −1,25
Робота в групах:
С
1. Позначте на координатній прямій точки, що відповідають числам: 0; 3; 5; -6; -3; -7,5; 7. Порівняйте числа:
0 і 3; 5 і -7,5; -6 і -3;
-3 і 7; 3 і -7,5; 0 і -6.
2. Розташуйте в порядку зростання числа:
-5; 6,1; 0,2; -7,8; 0; -15.
Д
1. Між якими послідовними цілими числами розміщене число −4,3; 0,28; −0,65; − 
. ?
2. Запишіть усі цілі числа, що розташовані між числами:
а) − 3 і 2; б) − 5 і 1,5; в) − 7 і − 3
3. Знайдіть усі цілі числа, для яких виконується умова:
а) − 3 < х < 4; б) − 0,5 < х ≤ 4,3;
в) − 6,5 < х < 0.
В
1. Запишіть найбільше і найменше цілі числа, для яких виконується умова −36 ≤ х < −10.
2. На координатній прямій позначили числа а,в,с,d:
О
а в 0 с d порівняйте числа: а і в; в і с; с і d; - d і 0;
0 і с; -в і а.
Робота в парах
С
1. Обчисліть у зручний спосіб:
а) 13 + (−15) + 15 + 17; б) − 60 + 47 + (−37)
в) − 90 + 90 + (−113); г) 0 + (−8) + (−12) + 6
д) − 99 + (−500) + 600 + (−1)
2. Дано числа 1,5; -3,5; -2,5. Знайдіть
А) число, протилежне сумі цих чисел; Б) суму чисел, протилежних даним.
Д
1. Розв’яжіть рівняння:
а) х − 1 
= −2 
; б) у − 1 
= −3 
;
в) х − 6 
= −1 
.
2. Знайдіть значення виразу у найбільш зручний спосіб:
а) − 5,32 + (−11,9) + (−3,68)
б) 5,95 + (−7,64) + (−1,36) + 4,05
3. Обчисліть значення виразу
а + в + с, якщо а = −24; в = 7; с = −16
В
1. Знайдіть значення виразу, попередньо спростивши його: −2,8 + х + 7,26 + (−1,2) + у + (−9,26), якщо х = −4,8; у = 2,4.
2. За якої умови рівність х + 𝑦 + 𝑧 + 𝑡 = 0, якщох і у − протилежні числа?
Робота в парах
С
1. Розкрийте дужки:
а) 25 + (а − в); б) − 3 − (7 + п);
в) 3,5−(-а –в+с)
2. Розкрийте дужки і знайдіть значення виразу:
а) 10— 52 − 10; б) − 0,6 + (−5,1 + 4,5);
в) 8,3 − (5,81 − 4,1); г) − (13 − 93) − (102 − 43)
3. Розкрийте дужки і спростіть вираз:
а) 11 − (а + 25); б) − (5 − а + 3) − 93;
в) − (с + 5) + (34 + с − 5); г) − 31 − (75 − а)
д)— 4 + а − 64.
Д
1. Розкрийте дужки і знайдіть значення виразу:
а) (−2,5 + 3,6) − (9,8 − 7,3);
б) 36 − (2,15 + 3,5 − 4,1)
в) − (−3,24 − 7,04 + 8,1) − 2,1
2. Знайдіть різницю і спростіть її вираз:
а) в − с і − с + в − 10 б) а − с і − а + с − 5
в) − а + в + р і в − а − 4; г) а + в і а − в − с
В
1. Візьміть у дужки два останні доданки, поставивши перед дужками знак «+»; знак «-»:
а) 3 + 10 − 7 б) с − р + 17; в) 10 − а + в
г) 6 − а − в; д) − 5 + а + в; е) − 3 − а − 6
2. Розв’яжіть рівняння, попередньо його спростивши:
а) 6,5— 2,4 + х = 13; б) (х + 3,2) − 15 = 1,5
в) − (х − 4,5) + 3,22 = 0,8
г) − 10 + (10,7 − х) = 1,2
Робота в групах
С
1. Виконайте множення:
а) 
б) − 0,5 ∙ 0,2 ∙ (−0,25) ∙ 2 ∙ 5 ∙ (−4)
2. Спростіть вираз:
а) − 5,6х ∙ 10; б) 2,5а ∙ (−4)в;
в)
х(−1,5) ∙ (−2); г) − 0,4 ∙ (−2,5в) ∙ 2
д) − 5а ∙ (−0,4в) ∙ 3; е) − 2в ∙ (−8).
3. Обчисліть:
а) (−2)3 ∙ (−3)2; б) (−5)2 ∙ (−3);
в) (−0,1)2 ∙ (−0,2)2 ∙ 25 ∙ 10.
Д
1. Спростіть вираз і знайдіть його значення:
а) 100 ∙ а ∙ (−0,8в), якщо а 
; в = −1 
.
б) 
, якщо х = −1;
у 
2. Розв’яжіть рівняння:
а)х ∙ (−8,5) = 0; б) (х − 10) ∙ 3,2 = 04
в) − х ∙ 2,25 = 0; г) (х − 3) ∙ (х + 4,5) = 0
3. Знайдіть добуток усіх цілих розв’язків нерівності −6 < х ≤ −0,8.
В
1. Обчисліть у більш зручний спосіб:
а) 
б) 
в) 
г) 
2. Визначте знаки чисел а,в і с, якщо ав > 0, вс < 0, ас < 0 і с найменше з чисел.
Робота в групах
С
1. Спростіть вираз і вкажіть його коефіцієнт:
а) 
; б) 
;
в) − 5а ∙ 7в; г) − 3,8х ∙ (−1,6) ∙ (−3,8у)
д) − 0,4 ∙ (−6,3 р) ∙ 2к; е) 
.
С
1. Спростіть вираз і вкажіть його коефіцієнт:
а)
; б) 
;
в)
; г) 4,2а(−1,8)(−2,5п)
2. Замість * поставте таке число, щоб справджувалася рівність.
а) ∗∙ а = а; б) ∗∙ а = −а; в) ∗∙ а = 0;
г) ∗∙ а = 1; д) ∗∙ а = −1.
В
1. Спростіть вираз і вкажіть його коефіцієнт:
а)
;
б) 
.
Робота в групах
С
1. Зведіть подібні доданки:
а) 8а − 15а + а; б) 7а − 10а + 3;
в) − 10х + 16х − 4х + х; г) 13х − 16 + 5в + 8х
2. Розкрийте дужки і зведіть подібні доданки:
а) 2(х − 5) − 6х; б) – (с − 7) − 3с;
в) − 3(5а + 1) − 7а; г) 3(6 − р) − 10м
Д
1. Спростіть вираз:
а) 
а + 1 
а − 
а; б) − 
х − х + 
х
в) − 
м − 
м − 
а; г) 
с − 1 
с + 
к + 
к
2. Розв’яжіть рівняння:
а) 2(х − 1) − х = 0; б) 3(а + 7) − 2а = −1;
В
1. Розв’яжіть рівняння:
а) 0,2(3х − 4) − 1,6(х − 2) = 0
б) 3,2 (1 − 2х) − 0,7(3х − 1,5) = 5
2. Спростіть вираз і обчисліть його:
−0,8х − 2,2х + 4,2х − 4,2х, якщо х = 1,5
Робота в групах
С
1. Розв’яжіть рівняння:
а) 3,5(х − 3) − 0,7(7 − х) = −7
б) 3(2х + 1) = 9х
в) 1,7х + 2,04 = −6,8х
г) 9х − 8 = 4(х − 4 )
д) 3(2х + 7) + 4 = 5(х − 3)
Д
1. Розв’яжіть рівняння:
а) 2,3(5 − 3к) + 7,6(к − 2) = −1,46
б) 3,1(2 − х) + 4,5 = 7,2 − 4,3(х − 3,7)
2. Розв’яжіть рівняння, використовуючи основну властивість пропорції:
а) х−3 ; б) 3 = 5 ;
2х−1 3х−2
в) 12 ; г) 0,3 = −6 . х−1
В
1. За якого значення а рівняння 4ах = 15 − х має корінь, що дорівнює 3?
2. За яких значень а рівняння не має коренів
а) ах = 2; б) (а − 3)х = 5?
3. Знайдіть усі цілі значення р за яких корінь рівняння є натуральним числом:
а) рх = 10; б)(р + 2)х = −12?
Робота в групах
С
1. Побудуйте трикутник АВС, у якому АВ ⊥ ВС. Проведіть через точку А пряму, паралельну стороні ВС.
2. На площині через точку А проведені три прямі. Скільки прямих кутів може при цьому утворитися.
Д
1. Побудуйте чотирикутник АВСД, у якому тільки одна пара паралельних сторін і дві пари перпендикулярних сторін.
2. На площині через точку А проведено п’ять прямих. Яка найбільша кількість прямих кутів може при цьому утворитися?
В
1. Побудуйте п’ятикутник АВСДЕ, у якому ВС∥ ДЕ, АВ ⊥ ВС.
2. На площині через точку А проведено вісім прямих. Яка найбільша кількість прямих кутів може при цьому утворитися?
Робота в групах «Змагання художників»
1. Накресліть на координатній площині замкнену ламану, послідовними вершинами якої є точки:
(8;0); (6;2); (0;6); (1;4); (-1;4); (-3;3);(-6;0); (-8;0); (-6;1); (-6;-2,5); (-5;-1); (-1;1);(0;1); (3;0);(2;-1);(5;-1); (6;-2); (7;-2) (9;-3);(8;-1) та точку (7;-1). Дельфін радо вітає вас!
2. (-5;3);(-2;1);(1;2);(2;3);(6;4);(-2;6); (-3;3); (-3;4); (-2;5); (-
2;3); та чотири відрізки з кінцями (-6;7) і (-2;6); (2;7) і (2;6); (5;3) і (7;5); (5;5) і (7;3).
Вертоліт до польоту готовий!
3. (1;7);(0;10); (-1;11); (-2;10);(0;7);(-2;5); (-7;3); (-8;0); (-
9;1); (-9;0); (-7;2); (-2;-2); (-3;-1);(-4;-1); (-1;3); (0;-2); (1;2); (0;0); (0;3); (1;4); (2;4); (3;5); (2;6); (1;9); (0;10) та точку (1;6). Яку тварину намальовано?
4. (0;0); (-1;1); (-3;1); (-2;3); (-3;3); (-4;6); (0;8); (2;5); (2;11);
(6;10); (3;9); (4;5); (3;0); (2;0); (1; -7); (3; -8); (0;-8); (0;0).
Що за птах?
5. (1; -1); (-6;-1); (-6;6); (-7; -6);(-7; -5); (-8;4); (-8;8); (-6;9); (-6;10); (-5;10); (-5;4); (-1;6); (6;3); (6;-1); (5;-1); (5;1);
(4;1); (4;-6); (3;-6); (3;-2); (1;-1). Що за звір?
Завдання для роботи в парах чи групах. Заповніть ланцюжок обчислень:
+(-2,6) +5 +(-10) +(-0,1)
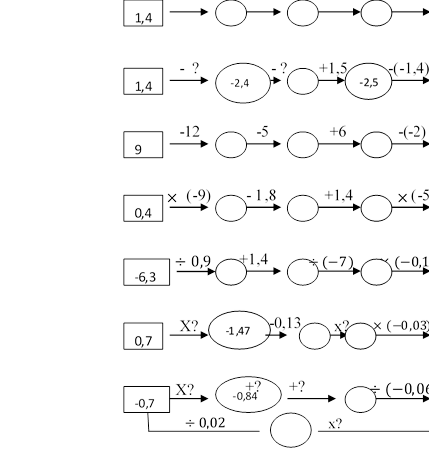
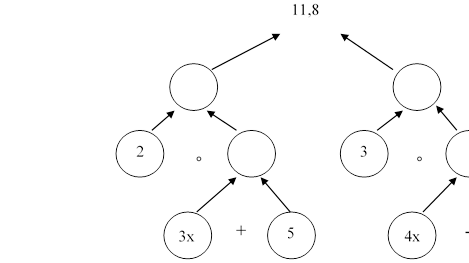
За схемою складіть і розв’яжіть рівняння:
Заповніть порожні клітинки квадрата так, щоб добуток усіх чисел на кожній вертикалі, горизонталі, діагоналі дорівнював одному й тому самому числу.
|
|
|
|
|
-1 |
-4 |
|
|
|
|
32 |
про публікацію авторської розробки
Додати розробку