Методична розробка "Використання програмного забезпечення GeoGebra на уроках математики"

Про матеріал

Розглянуто приклади можливого застосування GeoGebra під час вивчення різних тем шкільного курсу математики. Надаються рекомендації щодо роботи з цією програмою. Розглянуто її роль в покращенні навчання математики та сприянні використанню технологій в освіті. GeoGebra корисна різним категоріям користувачів, включаючи вчителів, студентів, науковців та інших фахівців у галузі математики та наукових дисциплін.

Перегляд файлу

Тодорова Наталя Дмитрівна

вчитель математики

2024 р.

АНОТАЦІЯ

Розробка GeoGebra в математиці є постійним процесом, спрямованим на надання вчителям та учням ефективних інструментів для вивчення та викладання математики.

Програма GeoGebra є однією з передових програм у сфері інформатизації шкільної математичної освіти. Її інтерактивні можливості та візуалізація роблять математику доступною та захопливою для сучасних учнів.

Вивчення GeoGebra допомагає учням розвивати комп’ютерну грамотність та навички використання сучасних технологій, що стає більш важливим у майбутньому.

GeoGebra корисна різним категоріям користувачів, включаючи вчителів, студентів, науковців та інших фахівців у галузі математики та наукових дисциплін.

Ключові слова: комп’ютерні технології, програма GeoGebra, динамічне середовище, інтерфейс програми, математика.

ЗМІСТ

ВСТУП…………………………………………………..……………………....3

РОЗДІЛ І. ПРО ПРОГРАМУ GEOGEBRA, АКТУАЛЬНІСТЬ ТА РЕКОМЕНДАЦІЇ ЩОДО РАБОТИ…………………………………………..5

1.1. Програма GeoGebra у світі та в Україні…………………………...….….5

1.2. Рекомендації щодо роботи з програмним забезпеченням GeoGebra .....6

1.3. Актуальність використання GeoGebra в шкільному навчанні…..….….8

РОЗДІЛ ІІ. ЗАСТОСУВАННЯ ПРОГРАМИ GEOGEBRA НА УРОКАХ МАТЕМАТИКИ, АЛГЕБРИ ТА ГЕОМЕТРІЇ………………………………10

2.1.Застосування програми GeoGebra на уроках математики в 6 класі НУШ…………………………………………………………………….….….10

2.2.Застосування програми GeoGebra на уроках алгебри в 9 класі…...…...14

2.3.Застосування програми GeoGebra на уроках геометрії в 11 класі…..…17

ВИСНОВКИ…………………………………………………...........................20

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ……………..………………….......21

ДОДАТОК А…………………………………………………..…..…….….…22

ВСТУП

Чи готові ми до життя в XXI столітті? Чи готові «пропускати через себе» нову інформацію та використовувати сучасні комп’ютерні і телекомунікаційні технології для навчання?

Готовність до використання сучасних технологій у навчанні та роботі стає обов’язковою, і вона включає в собі різні аспекти, які охоплюють технічні, соціальні та культурні компетенції.

Комп’ютерні технології стають необхідною частиною повсякденного життя молодого покоління, приваблюючи їх своєю універсальністю та можливостями.

Програма GeoGebra - одна із перспективних напрямків інформатизації шкільної математичної освіти. ЇЇ широко використовують у світі.

Мета роботи полягає в обґрунтуванні призначення комп’ютерного програмного забезпечення GeoGebra щодо використання на уроках математики.

У сучасному педагогічному суспільстві існує об’єктивна потреба в удосконаленні інформаційної компетентності педагога. Інформаційні технології стрімко розвиваються, і вони стають необхіднішим інструментом в освіті. Педагоги повинні триматися в тренді й оволодівати новими інструментами та ресурсами для підтримки сучасного навчання. Зростає значення цифрової освіти, яка передбачає використання інформаційних технологій у навчальному процесі. Педагоги мають бути інформованими та вміти ефективно впроваджувати ці технології в свою роботу. Завдяки розвитку Інтернету зростає попит на онлайн-навчання та використання електронних ресурсів. Педагоги повинні володіти інформаційною компетентністю для побудови ефективних онлайн-уроків та використання цифрових матеріалів. У сучасному світі робоче середовище вимагає вміти користуватися інформаційними технологіями. Педагоги повинні готувати учнів до майбутньої роботи, розвиваючи їх інформаційну компетентність.

Тому, вважаю, обговорення цієї теми дуже актуальним.

Для найкращого розкриття цієї теми поставлено ряд завдань:

 опрацювати наукову літературу та інформацію мережі Інтернет про використання програми GeoGebra у світі та в Україні;

 ознайомитися з елементами інтерфейсу програмного забезпечення GeoGebra;

 розробити рекомендації щодо роботи з цим програмним забезпеченням;

 розглянути актуальність використання GeoGebra в шкільному навчанні;

 розробити власні завдання з використання програми GeoGebra;

 провести відповідний аналіз результатів роботи та зробити висновки.

При роботі з GeoGebra в математичній освіті можна очікувати ряд значущих результатів для якісного засвоєння матеріалу та розвитку математичних навичок. Однак важливо зазначити, що успіх використання програмного забезпечення залежить від правильного планування уроків та налаштування завдань.

Начало формы

РОЗДІЛ І. ПРО ПРОГРАМУ GEOGEBRA, АКТУАЛЬНІСТЬ ТА РЕКОМЕНДАЦІЇ ЩОДО РАБОТИ

1.1. Програма GeoGebra у світі та в Україні

Програма GeoGebra виникла в 2002 році як дипломний магістерський проект Маркуса Хохенватера під час його навчання в університеті Зальцбурга. Протягом наступних років GeoGebra перетворилась на міжнародний проєкт з відкритим кодом, що активно розвивається і над яким зараз працює інтернаціональна команда з 20 розробників та більше, ніж 100 перекладачів. На даний момент система динамічної математики GeoGebra— це вільний продукт, який поєднує динамічну геометрію, алгебру, математичний аналіз і статистику.

GeoGebra, дійсно, отримала численні нагороди за свої досягнення в області освіти. Програма, яка на даний момент підтримується більш, ніж 50 мовами, завоювала визнання у різних країнах світу.

GeoGebra отримала нагороди за свою важливу роль в покращенні навчання математики та сприянні використанню технологій в освіті. Ці нагороди мають вагомий внесок GeoGebra в освітню сферу, його інноваційні можливості допомагають вчителям та учням у вивченні математики та інших наук.

В Україні започатковано регіональні інститути GeoGebra в Харкові й Чернігові. Вони є складовими Міжнародного Інституту GeoGebra (http://geogebra.org/igi) і розділяють його цілі й завдання. «Інститут GeoGebra Харків, Україна» засновано 6 липня 2010 року на базі кафедри інформатики Харківського національного педагогічного університету імені Г. С. Сковороди. [5;с.49].

Ці інститути зазвичай служать центрами, де вчителі та інші освітяни можуть отримати підтримку, навчання та ресурси для ефективного використання програми GeoGebra в своїх навчальних практиках.

1.2. Рекомендації щодо роботи з програмним забезпеченням GeoGebra

Вивчення програмного забезпечення GeoGebra може бути корисним для вчителів та учнів, які хочуть використовувати цей інструмент для вивчення та навчання математики.

Першим кроком буде завантаження та встановлення GeoGebra на комп’ютер з офіційного веб-сайту (https://www.geogebra.org/download). Відкрийте програму і запустіть GeoGebra на вашому пристрої після встановлення.

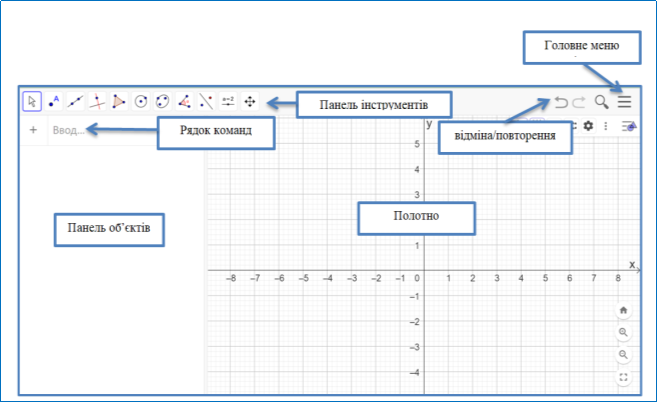
Слід ознайомитися з інтерфейсом програми. Він нагадує класну дошку, на якій можна будувати графіки функції. Основні елементи інтерфейсу: (Додаток А).

 головне меню: основні функціональні можливості програми GeoGebra;

 панель інструментів: на ній знаходиться набір кнопок швидкого доступу до інструментів, які дозволяють виконувати побудову об’єктів за допомогою миші;

 полотно: основна область, у якій створюються об’єкти;

 панель об’єктів: область, у якій записуються усі об’єкти, створені на полотні (навіть приховані);

 рядок команд: область, яка дозволяє вводити різні команди, форми, рівняння тощо. Після введення команди і натискання Enter інформація про об’єкт відображається в панелі об’єктів, а сам об’єкт зображується на полотні;

 відміна/повторення: дві кнопки, ліва дозволяє скасувати останню дію, права – повернути скасовану.

Почніть з вивчення геометричних конструкцій. Спробуйте створити прості геометричні фігури, лінії, точки, кола тощо. Використовуйте інструменти для вимірювання відстаней та кутів. Експериментуйте та спробуйте зрозуміти, як вони працюють.

Досліджуйте алгебраїчні можливості GeoGebra. Створюйте алгебраїчні вирази та функції, будуйте графіки, розв’язуйте алгебраїчні рівняння.

Досліджуйте тригонометричні функції, будуйте їх графіки, вивчайте взаємозв’язок між різними тригонометричними виразами.

Ознайомтеся з інтерактивними інструментами GeoGebra, такими як рухливі точки, анімації та інші, щоб створювати динамічні та цікаві візуалізації.

Розгляньте можливості використання GeoGebra у своєму навчальному процесі. Спробуйте створювати власні уроки та завдання для учнів.

Використовуйте доступні навчальні ресурси та онлайн-матеріали, щоб поглибити свої знання про використання GeoGebra

Якщо не зрозуміло, використовуйте розділ «Допомога» на веб-сайті GeoGebra та розділ документації для отримання інструкцій та порад. Також, на сайті є безліч відеоуроків та матеріалів для самостійного вивчення.

GeoGebra має активну спільноту користувачів. Долучіться до форумів, де ви можете задавати питання, ділитися досвідом та отримувати підтримку від інших користувачів.

Загалом, експериментуйте та освоюйте GeoGebra крок за кроком. Воно стане потужним інструментом для вивчення математики та інших наук.

1.3. Актуальність використання GeoGebra в шкільному навчанні

GeoGebra є однією з передових програм у сфері інформатизації шкільної математичної освіти. GeoGebra - це вільне програмне забезпечення, яке інтегрує геометричні, алгебраїчні та тригонометричні поняття в єдиному середовищі. Воно має безкоштовну версію, яку можна використовувати як учителям, так і учням, щоб покращити процес навчання та розуміння математики.

GeoGebra впроваджує сучасні технології в освітній процес. Його інтерактивні можливості та візуалізація роблять математику доступною та захопливою для сучасних учнів.

GeoGebra дозволяє легко переходити від геометричних об’єктів до алгебраїчних виразів та навпаки. Це полегшує вивчення та розуміння взаємозв’язку між цими двома гілками математики.

Програма є гнучкою та може використовуватися в різних рівнях освіти - від школи до вищих навчальних закладів. Її можна використовувати для навчання різних математичних концепцій та наукових дисциплін.

Можна створювати динамічні конструкції, де об’єкти можуть змінюватися за допомогою параметрів або пересуватися за допомогою анімації. Це робить математику більш доступною та захоплюючою. А учні можуть експериментувати та спостерігати за змінами в реальному часі.

GeoGebra надає можливості для індивідуалізації навчання, дозволяючи учням працювати власним темпом та досліджувати матеріал самостійно.

Інтерактивні та цікаві візуалізації у GeoGebra можуть зробити вивчення математики захоплюючим та стимулюючим предметом для учнів, зокрема для тих, хто може відчувати виклики при традиційному навчанні.

GeoGebra надає різноманітні навчальні ресурси та матеріали для вчителів, щоб допомогти їм ефективно використовувати програму в навчальному процесі.

Програма підтримує роботу з графіками функцій, геометричними об’єктами, алгебраїчними виразами, тригонометричними функціями тощо.

Вчителі можуть створювати інтерактивні уроки та завдання, що забезпечить більш ефективне вивчення та залучить учнів до роботи.

Вивчення GeoGebra допомагає учням розвивати комп’ютерну грамотність та навички використання сучасних технологій, що стає все більш важливим у майбутньому.

Безкоштовна версія GeoGebra є доступною для вчителів та учнів з усього світу. Це робить програму доступною для використання у різних навчальних установах.

Так, програма GeoGebra є дуже актуальною та має значну кількість функціональних можливостей, які роблять її популярною серед вчителів та учнів.

РОЗДІЛ ІІ. ЗАСТОСУВАННЯ ПРОГРАМИ GEOGEBRA НА УРОКАХ МАТЕМАТИКИ, АЛГЕБРИ ТА ГЕОМЕТРІЇ

2.1.Застосування програми GeoGebra на уроках математики в 6 класі НУШ

Вивчення координатної площини у 6 класі може бути цікавим та захоплюючим. Це базовий етап в математичному навчанні, де учні вперше стикаються з поняттям координат та графіків.

У 6 класі Нової української школи (НУШ) можна використовувати GeoGebra для різноманітних вправ при роботі з координатами, які відповідають вимогам програми.

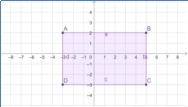
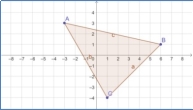
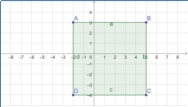$C:\Users\Вчитель\AppData\Local\Packages\Microsoft.Windows.Photos_8wekyb3d8bbwe\TempState\ShareServiceTempFolder\geogebra-export (45).jpeg$ $C:\Users\Вчитель\AppData\Local\Packages\Microsoft.Windows.Photos_8wekyb3d8bbwe\TempState\ShareServiceTempFolder\geogebra-export (43).jpeg$ $C:\Users\Вчитель\AppData\Local\Packages\Microsoft.Windows.Photos_8wekyb3d8bbwe\TempState\ShareServiceTempFolder\geogebra-export (44).jpeg$ Учні можуть використовувати GeoGebra для побудови простих геометричних фігур, таких як квадрати, прямокутники, трикутники тощо. Завдання може включати визначення координат вершин, знаходження відстані між точками, обчислення периметра та площі фігур (рис.2.1-2.3).

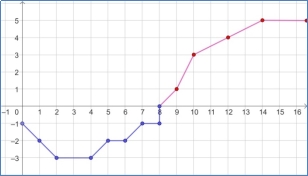$C:\Users\Вчитель\AppData\Local\Packages\Microsoft.Windows.Photos_8wekyb3d8bbwe\TempState\ShareServiceTempFolder\geogebra-export (46).jpeg$ рис. 2.1. рис. 2.2. рис.2.3. Використання GeoGebra для побудови графіків простих функцій. Завдання може включати аналіз графіків, визначення значень функцій при конкретних аргументах та встановлення взаємозв’язку між графіками. Створення графіків залежності температури від часу (рис.2.4).

рис. 2.4.

Побудова малюнків з використанням координат може бути захоплюючим цікавим завданням для учнів. Використання GeoGebra чи подібних інструментів може полегшити цей процес та надати можливість учням візуалізувати математичні концепції.

Побудова малюнків за координатами у GeoGebra є досить простою і цікавою задачею. Потрібно використовувати інструменти для роботи з точками, відрізками та іншими об’єктами на координатній площині.

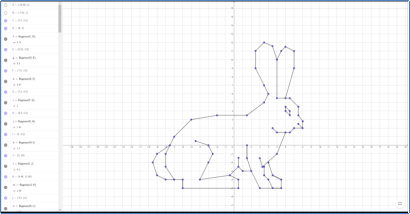
$C:\Users\Вчитель\AppData\Local\Packages\Microsoft.Windows.Photos_8wekyb3d8bbwe\TempState\ShareServiceTempFolder\qrcode_103320982_a0bab51985d75a1f39b22cb9bb4023f8.jpeg$ Відкрийте GeoGebra та використовуйте інструмент «Точка» для створення точок на координатній площині. Кожна точка буде мати свої координати (x, y). Використовуйте інструмент «Відрізок» для створення відрізків, які з’єднують точки і створюють малюнок. Координати точок визначають форму та розташування малюнка (рис. 2.5).

рис. 2.6.

рис. 2.5.

Перейдіть за QR-кодом (рис.2.6) або за посиланням на особисту сторінку https://www.geogebra.org/m/fjrq8rek до власного створеного малюнку за координатами на платформі GeoGebra (рис.2.5).

Змінюйте координати точок, довжини ліній або інші параметри, щоб експериментувати та помічати, як зміни впливають на ваш малюнок. Після завершення побудови вашого малюнка збережіть його у GeoGebra або поділіться посиланням, щоб інші користувачі також могли переглядати вашу роботу.

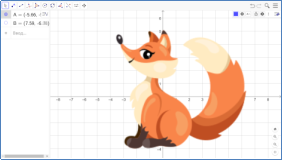Також можна самостійно створити будь-який малюнок з використанням координат з фото з Інтернету. Треба знайти зображення без фону. Імпортувати в GeoGebra це зображення (рис.2.7). Воно з’явиться на робочому аркуші. Використовуйте команди GeoGebra для створення об’єктів (точок, відрізок) на базі вашого зображення (рис.2.8).

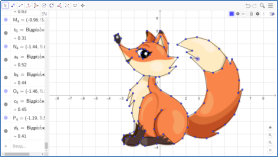
рис.2.7. рис.2.8.

Будьте уважні при виборі фотографій, оскільки їх може бути важко адаптувати для створення точних координатних малюнків в GeoGebra (рис.2.9). Начало формы рис.2.9.

Потім з панелі команд переписати координати точок.

Можна створювати математичні завдання та головоломки за допомогою GeoGebra, які допомагають учням розвивати аналітичні навички та креативне мислення.

Створення танграма в GeoGebra для учнів 6 класу Нової української школи (НУШ) може бути цікавим завданням для вчителя.

Танграм - це популярна геометрична головоломка, яка складається з семи геометричних фігур (п’ять трикутників, квадрат та паралелограм), які можна скласти в квадрат. Ось як можна створити танграм у GeoGebra:

1) спочатку створіть п’ять трикутників, які будуть складати танграм. Використовуйте інструмент «Трикутник» та зазначте координати вершин для створення кожного трикутника;

2) створіть квадрат, який буде основою танграма. Використовуйте інструмент «Квадрат» та визначте координати його вершин;

3) додайте паралелограм, який буде складатися з двох трикутників та сторінки квадрата. Визначте координати вершин для створення паралелограма;

4) групуйте всі створені об’єкти (трикутники, квадрат, паралелограм) так, щоб їх можна було переміщати як єдиний танграм. Застосуйте інструмент «Група» для цього;

$C:\Users\Вчитель\AppData\Local\Packages\Microsoft.Windows.Photos_8wekyb3d8bbwe\TempState\ShareServiceTempFolder\qrcode_103329861_8baf3bfe875d5e77e688405262eb2f06.jpeg$ 5) застосуйте інтерактивність, щоб учні могли пересувати та обертати танграм. Додайте слайдери для зміни розмірів об’єктів.

рис.2.11.

рис. 2.10.

Перейдемо за QR-кодом (рис.2.11) або за посиланням на особисту сторінку https://www.geogebra.org/m/cgcqrjqq до власної творчої інтелектуальної гри танграм на платформі GeoGebra (рис.2.10).

Застосування GeoGebra для вивчення танграма не тільки сприяє розвитку геометричних навичок учнів, але й робить уроки більш цікавими та інтерактивними.

2.2.Застосування програми GeoGebra на уроках алгебри в 9 класі

GeoGebra - це динамічна математична програма, яка поєднує геометрію, алгебру, таблиці, графіки та статистику в одному середовищі. Ця програма може бути використана для вивчення та візуалізації різних математичних концепцій, включаючи графіки функцій та їх перетворення.

$C:\Users\Вчитель\AppData\Local\Packages\Microsoft.Windows.Photos_8wekyb3d8bbwe\TempState\ShareServiceTempFolder\qrcode_103351430_fa615b3de0df1b8ebcc2fa9a926f5df7.jpeg$ Вивчення перетворень графіків функцій є важливою частиною курсу алгебри у 9 класі. Перетворення графіків включає зміни у функції, такі як зсув, стиснення, розтягнення та відображення.

рис.2.13.

рис.2.12.

Перейдемо за QR-кодом (рис.2.13) або за посиланням на особисту сторінку https://www.geogebra.org/m/y4zfutha до власної розробки на платформі GeoGebra до теми «Перетворення графіків функцій» для 9 класу (рис.2.12).

На одному полотні було створено два графіка функцій: і де – будь-які числа.

Також було створено поле введення, де у графі можна вводити будь-яку функцію і, натиснувши «Enter», бачимо два графіка функцій.

Для функції будується графік, і цей графік на полотні відображається помаранчевим кольором. Для функції будується графік, і цей графік на полотні відображається синім кольором, а до чисел створено повзунки від -5 до 5.

За допомогою повзунка до числа можна побачити зміну графіка:

- якщо : графік розтягнувся від осі у разів;

- якщо графік стиснувся до осі у разів.

За допомогою повзунка до числа можна побачити зміну графіка:

- якщо : графік зробив перенесення вздовж осі на одиниць вліво;

- якщо графік зробив перенесення вздовж осі на одиниць вправо.

За допомогою повзунка до числа можна побачити зміну графіка:

- якщо : графік зробив перенесення вздовж осі на одиниць угору;

- якщо графік зробив перенесення вздовж осі на одиниць униз.

Побудова графіків функцій з модулем у GeoGebra виявляється простою інтерактивною задачею.

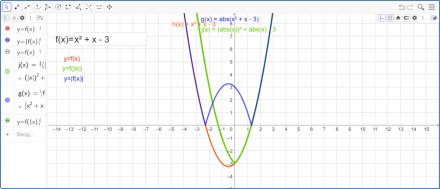
$C:\Users\Вчитель\AppData\Local\Packages\Microsoft.Windows.Photos_8wekyb3d8bbwe\TempState\ShareServiceTempFolder\qrcode_103351533_a56f3fe491e17adc26e41a95a69a5238.jpeg$ У GeoGebra використовується функція , де - це вбудована функція для обчислення модулю числа. Введення функції може бути виконано в поле «Введення» і просто натискайте «Enter» для побудови графіка.

рис.2.15.

рис.2.14.

Перейдемо за QR-кодом (рис.2.15) або за посиланням на особисту сторінку https://www.geogebra.org/m/tdm8r2xq до власної розробки на платформі GeoGebra до теми «Перетворення графіків функцій з модулем» для 9 класу (рис.2.14).

Геометричне представлення функцій з модулем може бути особливо корисним для розуміння їхнього характеру та властивостей. Ці перетворення можуть застосовуватися і поєднуватися для створення більш складних змін у графіках функцій. GeoGebra надає можливість вивчати математику в інтерактивний спосіб, дозволяючи учням експериментувати з концепціями та візуально сприймати математичні властивості та зв’язки.

Начало формы

2.3.Застосування програми GeoGebra на уроках геометрії в 11 класі

Використання GeoGebra на уроках геометрії для учнів 11 класів може значно покращити розуміння учнів та зацікавити їх у навчальному матеріалі.

В стереометрії розгортка – це плоска фігура, яку можна отримати розкриваючи поверхню тривимірного об’єкта і відображаючи її на плоску площину. Розгортка може бути використана для побудови та аналізу геометричних фігур. Наприклад, для обчислення площі поверхні складеної фігури або визначення її геометричних характеристик.

Розгортка допомагає з’ясувати, які частини поверхні об’єкта взаємодіють у відповідних видових проекціях та кутах спостереження.

У географії розгортка також використовується для вивчення карт та глобусів, де поверхня Землі проектується на плоску карту.

$C:\Users\Вчитель\AppData\Local\Packages\Microsoft.Windows.Photos_8wekyb3d8bbwe\TempState\ShareServiceTempFolder\qrcode_103444763_e7180b7952f7d14b5f707cf89d9ae0cc.jpeg$ Розгортка допомагає вирішити завдання, пов’язані із складними тривимірними об’єктами, і забезпечує можливість аналізу їх структури та властивостей в площині.

рис.2.17. Начало формы

рис.2.16.

Перейдемо за QR-кодом (рис.2.17) або за посиланням на особисту сторінку https://www.geogebra.org/m/krpwcfz9 до власної розробки на платформі GeoGebra розгортка призми (рис.2.16).

Використання GeoGebra на уроках геометрії в 11 класі для побудови вписаної піраміди у циліндр може стати цікавим та педагогічно ефективним методом навчання.

Використовуйте інструменти для побудови циліндра та піраміди, а також для роботи з точками, відрізками та геометричними об’єктами. Створіть анімацію, де піраміда поступово вписується у циліндр. Використовуйте анімаційні команди для поетапної побудови об’єктів, щоб учні могли відстежувати кожен етап процесу. Досліджуйте властивості вписаної піраміди та її взаємодію з циліндром. Вимірюйте різні параметри, такі як висота, радіуси та кути і аналізуйте їх взаємозв’язок.

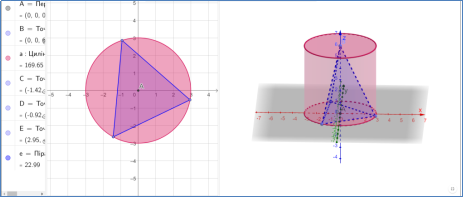
$C:\Users\Вчитель\AppData\Local\Packages\Microsoft.Windows.Photos_8wekyb3d8bbwe\TempState\ShareServiceTempFolder\qrcode_103446954_48fa6e43fbf8af757bf5d56ab7a7b1fa.jpeg$ Вивчайте можливості графічного представлення побудови та властивостей об’єктів у GeoGebra. Використовуйте різні кольори та стилі для кращого розуміння геометричних взаємодій.

рис.2.19.Начало формы

рис.2.18.

Перейдемо за QR-кодом (рис.2.19) або за посиланням на особисту сторінку https://www.geogebra.org/m/wf6dqmbq до власної розробки на платформі GeoGebra піраміда вписана у циліндр (рис.2.18).

Застосування GeoGebra для побудови вписаного конуса в куб на уроках геометрії може бути цікавим та пізнавальним завданням для учнів. Використовуйте інструмент «Куб» для побудови тривимірного куба. Задайте його розміри та положення.

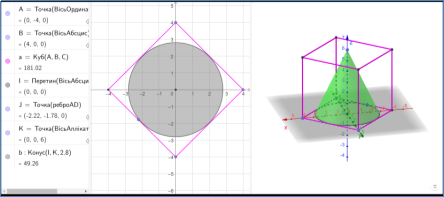
$C:\Users\Вчитель\AppData\Local\Packages\Microsoft.Windows.Photos_8wekyb3d8bbwe\TempState\ShareServiceTempFolder\qrcode_103447460_696673a258c263919e800a0d212c39d8.jpeg$ Використовуйте інструмент «Конус» для побудови вписаного конуса у куб. Важливо, щоб вершина конуса знаходилася в центрі куба, а основа доторкалася до поверхні куба. Змінюйте розміри та положення конуса за допомогою інструментів зміни розмірів та переміщення. Спостерігайте, як зміни впливають на взаємодію конуса та куба.

рис.2.21.

рис.2.20.

Перейдемо за QR-кодом (рис.2.21) або за посиланням на особисту сторінку https://www.geogebra.org/m/h8e6gavz до власної розробки на платформі GeoGebra піраміда вписана у циліндр (рис.2.20).

Використання GeoGebra на уроках геометрії дозволяє створювати інтерактивні моделі, які полегшують розуміння геометричних концепцій та їх взаємодій. Активне вивчення таких об’єктів за допомогою програмного забезпечення може значно полегшити процес навчання та зробити його більш захопливим і цікавим для учнів.

ВИСНОВКИ

Працюючи над проблемою, я остаточно впевнилась, що ця тема є актуальною. І враховуючи те, як сучасні науково-технологічні процеси охоплюють весь світ, тема ще є й перспективною в наш час.

Використання GeoGebra на уроках математики може бути корисним:

для учнів: у розумінні абстрактних математичних концепцій через візуалізацію та інтерактивність; у розвитку навичок вирішення математичних завдань за допомогою геометричних конструкцій та алгебраїчних рівнянь; у сприянні активному вивченню та дослідницькому підходу до математики;
для вчителів: у ефективному використанні інтерактивних засобів для пояснення та демонстрації математичних концепцій; у розробці динамічних уроків, які відповідають різним стилям навчання учнів; у вивченні та вдосконаленні педагогічних методів за допомогою технології.
для закладів освіти: у підвищенні рівня математичної грамотності серед учнів; у забезпеченні доступу до інноваційних методів викладання та вивчення математики; у стимулюванні інтересу до математики через застосування сучасних технологій.

Отже, програмне забезпечення GeoGebra може бути корисним для всіх учасників навчального процесу, допомагаючи покращити розуміння та зацікавленість у математиці через використання інтерактивних інструментів та візуалізацію.

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

1.Горошко Ю. В. Використання комп’ютерних програм для створення динамічних моделей при вивченні математики / Ю. В. Горошко, Є. Ф. Вінниченко // Науковий часопис НПУ імені М. П. Драгоманова. Серія № 2 :

2.Комп’ютерно- орієнтовані системи навчання : зб. наук. праць / редрада. – К. : НПУ імені М. П. Драгоманова, 2006. – № 4 (11). – с. 56–62.

3. Мiлян, Р.С. GeoGebra як засіб формування логічної складової математичної компетентності учнів: матеріали III Міжнародної науково практичної iнтернет-конференцiї (м. Тернопіль, 5 квітня, 2019). Тернопiль : ТНПУ iм. В. Гнатюка, 2019. С. 141–143

4.Ракута В. М. GeoGebra для початківців : навчальний посібник / Ракута В. М. – Чернігів : ЧОІППО ім. К. Д. Ушинського, 2011. – с.49.

5.Ракута В. М. Програми для роботи з функціями та графіками / Ракута В. М. // Комп’ютер у школі та сім’ї. – 2010. – № 7 (87). – с. 29–33.

6.Ракута В.М. Система динамічної математики GEOGEBRA як інноваційний засіб вивчення математики / В.М.Ракута // Інформаційні технології і засоби навчання. 2012. №4 с.30.

7.Семенiхiна, О.В., Друшляк М.Г., Хворостiна Ю.В. Використання хмарного сервiсу GeoGebra у навчанні майбутніх учителів природничо-математичних дисциплін, Iнформацiйнi технології i засоби навчання. Київ, 2019. Т. 75, №5. С. 48–66.

8.GeoGebra Wiki [Електронний ресурс]. – Режим доступу: http://www.geogebra.org

9.https://ndavydkovo.blogspot.com/2016/03/blog-post_3.html

10.https://uk.wikipedia.org/wiki/%D0%93%D1%80%D0%B0%D1%84%D1%96%D0%BA_%D1%84%D1%83%D0%BD%D0%BA%D1%86%D1%96%D1%97

Додаток А

Рис.1.1

Начало формы