Міністерство освіти і науки України

Харківська загальноосвітня школа І-ІІІ ступеня №130             

Харківської міської ради Харківської області

 

 

 

 

 

 

 

 

 

 

 

 

Викладач математики

_Ляхова  

Тетяна Петрівна

 

Харків – 2018

 

 

 

 

 

 

 

 

 

 

 

1.                     Загальна характеристика теми.

2.                     Конспекти уроків.

3.                     Картки - завдання для самостійної роботи учнів.

4.                     Тестові завдання.

5.                     Задачі з професійною спрямованістю.

6.                     Завдання до тематичної атестації.

7.                     Позаурочний захід «Математичний футбол»

8.                     Додатки:

1)                     презентації уроків

2)                     презентація теми: «Паралельність прямих і площин в просторі»

3)                     математичний диктант

                9.     Література

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

У процесі вивчення даної теми поглиблюються знання учнів про аксіоматичну побудову математичної теорії, розвиваються їхні просторові уявлення. Вже з перших кроків вивчення стереометрії на перший план виступає ідея математичного моделювання реальних об'єктів і відношень між ними за допомогою найпростіших геометричних фігур і відповідних математичних відношень.

До найважливіших завдань вивчення теми належить розгляд одного з основних методів зображення просторових фігур на площині — методу паралельного проектування і формування найпростіших навичок його застосування.

Таким чином, основними завданнями вивчення теми є:

 

− формування в учнів розуміння того, що просторові геометричні фігури є математичними моделями об'єктів навколишнього середовища;

− розвиток в учнів уявлень про дедуктивний метод;

− систематизація уявлень та знань учнів про взаємне розміщення прямих і площин у просторі; − ознайомлення учнів з методами побудови зображень фігур і виконання на них побудов.

Вивчення теми треба спланувати так, щоб після завершення навчання учні вміли: встановлювати у просторі взаємне розміщення прямих і площин, зокрема паралельність прямих, прямої і площини, двох площин, мимобіжність прямих;

будувати зображення фігури і на них виконувати нескладні побудови (елементів фігур, точок перетину прямої і площини, двох площин, перерізів куба, тетраедра та ін.); застосовувати відношення паралельності між прямими і площинами у просторі для опису об'єктів фізичного простору і відношень між ними.

 

Загальні методичні рекомендації

 

Розгляд теми «Паралельність прямих і площин» зводиться до вивчення взаємного розміщення прямих і площин, зокрема їхньої паралельності. 

При вивченні теми особливу увагу слід приділити класифікації взаємного розміщення прямих і площин у просторі. Учні мають зрозуміти, що всі наведені теореми спрямовані насамперед на те, щоб допомогти визначати відповідне розміщення.

Формування просторових уявлень учнів є одним з основних завдань теми. Водночас це одна з найскладніших педагогічних проблем. Тому з перших занять необхідно широко використовувати систему вправ на «відтворення» просторової ситуації за її описом чи рисунком. Важливе місце слід відвести навчанню учнів зображенню геометричних фігур і використанню цих зображень при розв'язуванні задач.

При вивченні даної теми закладається теоретична основа побудови зображень геометричних фігур. Це бажано зробити якомога раніше. Беручи за основу наведені міркування, передбачається вивчення паралельного проектування практично на початку теми.

 

 

 

 

 

 

 

Рекомендується також активно використовувати при вивченні даної теми найпростіші геометричні тіла (хоча б куб і тетраедр), «забігаючи» трішки наперед. Ці фігури дають змогу розглядати не тільки задачі на уявні побудови, а й побудови на проекційному рисунку, зокрема, побудову точки перетину прямої і площини та лінії перетину двох площин, побудову найпростіших перерізів.

При вивченні аксіом необхідно акцентувати увагу учнів на тому, що в будь-якій площині простору і лише у площині виконується планіметрія, тобто для використання планіметрії, перш за все, необхідно «увійти» в площину. З цієї точки зору дуже важливими є способи завдання (фіксації) площини. Ці ж способи важливі також для побудови перерізів.

 

Особливу увагу необхідно приділити реалізації прикладної спрямованості теми. Головним внеском у вирішення цієї проблеми є формування в учнів чітких уявлень про взаємозв'язки геометричних об'єктів і відношень між ними з об'єктами навколишнього середовища та відношеннями між ними.

У даній темі закладається фундамент побудови стереометрії. Тому важливо з самого початку акцентувати увагу на необхідності обґрунтування кожного кроку міркувань, прискіпливо аналізувати зміст понять, тверджень. Важливим є питання існування і однозначності об'єктів, про які йдеться. Існування чи не існування  якогось об'єкта доводяться конструктивно. Однозначність чи не існування доводяться, як правило, від супротивного. Ці загальні положення учні повинні засвоїти під час вивчення теми і застосовувати надалі.

 

Нижче наводиться орієнтовний план вивчення теми.

 

 

Тема 1.  Паралельність прямих і площин у просторі (22 год.)
1.	Повторення планіметрії. Діагностика готовності до вивчення стереометрії	2
2.	Основні поняття, аксіоми  стереометрії і найпростіші наслідки із них.	2
3.	Взаємне розміщення прямих у просторі.	4
4.	Паралельне проектування і його властивості. Зображення фігур у стереометрії.	4
5.	Паралельність прямої і площини.	3
6.	Паралельність площин.	4
7.	Тематичне оцінювання (повторення, систематизація, контролюючі заходи, коригувальна робота)	3

 

 

 

 

 

 

 

 

 

Урок 1. 

Тема. Основні поняття стереометрії. Аксіоми стереометрії.

 

Мета: сформувати в учнів уявлення про стереометрію як частину геометрії; ознайомити з основними поняттями стереометрії та аксіомами стереометрії. Розвивати просторове уявлення учнів.

 

Обладнання: моделі многогранників, презентація.

 

Тип уроку: засвоєння нових знань

 

Хід уроку

 

І. Організаційний момент.

 

ІІ. Узагальнення та систематизація знань учнів.

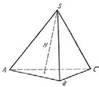
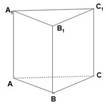
Назвіть фігури та об’єкти, які ви бачите (слайд2). З якими з них ви найчастіше мали справу на уроках геометрії? У кінці 9 класу ми познайомилися з многогранниками. Які ви запам’ятали? (демонстрація моделей + слайд 3). Давайте назвемо основні елементи прямокутного паралелепіпеда та піраміди (на моделях)

.

ІІІ. Формулювання мети, теми і завдань уроку. Сьогодні ваші знання розширяться, тому що ми будемо більш детально знайомитися з фігурами у просторі. А допоможе нам в цьому розділ геометрії – стереометрія (слайд 4). Історична сторінка (слайд5) + повідомлення учня.

 

ІV. Сприйняття та усвідомлення нового матеріалу.

Основні фігури у просторі  - точка,пряма, площина (слайд 6). Викладач наводить приклади матеріальних моделей площини – поверхня підлоги, стола, шибки. Приклади зображення площин, позначення точок і прямих учні занотовують у зошит.

Хто нагадає що таке аксіома? Аксіома – це твердження, яке не потребує доведення.

Наведіть приклади відомих вам аксіом.

Стереометрія теж має свої аксіоми (слайд 7). Учні схематично у зошит переносять малюнки.

 

V. Закріплення і осмислення нового матеріалу.

1. Робота за готовими малюнками (слайд 8 – 11). 2. Робота у різнорівневих групах  (слайд 12).

 

VІ. Підсумки уроку.

Що вивчає стереометрія?

Хто вважається автором терміну «стереометрія»? Як він переводиться?

Назвіть основні фігури у просторі.

Сформулюйте аксіоми стереометрії.

Оцінки за урок.

\VІІ. Домашнє завдання 

 

 

Урок 2. 

Тема. Існування площини, яка проходить через дану пряму і дану точку.

Мета: вивчення теореми про існування площини, яка проходить через дану пряму і дану точку, що не лежить на ній, як наслідок із аксіом стереометрії; учити застосовувати аксіоми і теорему при рішенні задач.

Обладнання: моделі многогранників, презентація. Тип уроку: засвоєння нових знань, формування вмінь.

 

Хід уроку.

І. Організаційний момент.

 

ІІ. Перевірка домашнього завдання. Математичний диктант (слайд2)

Користуючись зображенням, запишіть:

Точки, які належать площині грані АВС;

Точки, які не лежать у площині грані АВС;

Спільні точки площин граней АВС і АВS;

Пряму перетину площин граней АВС і SВС; Площину, яка проходить через прямі АВ і ВС;

Площину, яка не містить жодної із прямих АВ і ВС.

Математичний диктант (робота з карточками – останні учні ІІІ варіант).

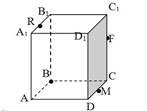Запишіть:

А) точки, що належать площині грані ABCD; (A, B, C, D, М)

Б) точки, що не лежать у площині грані ABCD; (A1, B1, C1, D1, R, F)

В) спільні точки площин граней ABCD і DCC1D1; ( D, M, C)

Г) пряму перетину площин граней ABCD і ВСС1В1; (BC)

Д) площину, що проходить через прямі АВ і В1В; (ABB1A1)

Е) площини, що не містять прямі АВ і В1В.( A1B1C1D1, DCC1D1)

Самоперевірка – звірити з правильними відповідями (слайд 2– І, ІІ варіант ), відкидна дошка (ІІІ варіант).

Сформулюйте аксіоми стереометрії. Яка з них дозволяє задати площину?

 

ІІІ. Формулювання теми уроку. Сприйняття й усвідомлення матеріалу.

Існує ще один спосіб визначення площини: через пряму і точку, яка їй не належить, можна провести площину і до того ж тільки одну. Цю теорему ми і доведемо з вами. (слайд 3 – існування площини)).

Нехай а – дана пряма і С – точка, яка їй не належить(якою аксіомою користуємося?).

Візьмемо точку D, яка лежить на прямій а(чому ми це можемо зробити?). Проведемо пряму DC.( на якій підставі?)

Через прямі а і DC проведемо площину α ( чим скористаємося?).

Слайд 4 – єдиність такої площини. Усні вправи – слайд 5 - 10.

 

ІV. Розв’язування вправ ( письмово) – слайд 11.

 

V. Підсумки уроку. Оголошення оцінок.

 

VІ. Домашнє завдання 

 

 

 

 

Урок 3. 

Тема. Перетин прямої з площиною. Перерізи многогранників.

Мета: ознайомлення учнів із взаємним розташуванням прямої і площини  у просторі. Вивчення теореми про належність прямої до площини. Формування поняття перерізу многогранника. Розвивати конструктивно-графічну компетентність.

Обладнання: моделі многогранників, презентація. Тип уроку: засвоєння нових знань, формування вмінь.

 

Хід уроку

 

І. Організаційний момент.

 

ІІ. Перевірка домашнього завдання. Група  учнів (4-5) заповнюють картки контролю теоретичних знань.

 

Варіант1	Прізвище,	Варіант1	Прізвище,
Якщо дві різні площини мають спільну точку, то __________________________ _________________________________ Через пряму і точку, ________________ ____________________________,   можна провести___________________________. Яке тіло зображено на малюнку?__________ Вкажіть : Ребра ________________ Вершини _____________ Грані ________________     Установіть відповідність між заданими многогранниками (1-3) та їхніми властивостями (А-Г): 1     прямокутний А має шість  паралелепіпед вершин 2     чотирикутна Б має шість  піраміда граней 3     трикутна В має шість ребер призма Г має вісім ребер   А Б В Г 1         2         3		Яка б не була площина, існують точки, які ____________________________________ ____________________________________. Якщо дві різні _____________, мають спільну точку, то _____________________ ______________і до того ж _____________  Яке             тіло             зображено           на малюнку?__________ Вкажіть : Ребра ________________  Вершини _____________ Грані ________________     Установіть відповідність між заданими многогранниками (1-3) та їхніми властивостями (А-Г): 1 прямокутний          А має десять вершин паралелепіпед           Б має чотири   грані      2 трикутна                 В має дванадцять     піраміда ребер                3 п’ятикутна              Г має вісім ребер  призма                              А Б В Г 1         2         3

 

Учень біля дошки доводить теорему про існування площини, яка проходить через дану пряму і дану точку.

 

 

 

 

 

 

Фронтальне опитування:

Скільки площин можуть задавати пряма і точка?

 

Скільки площин можуть задавати дві прямі, які перетинаються?

Скільки площин можна провести через три прямі, які мають спільну точку?

Скільки площин можна провести через пряму і три точки, які не лежать на цій прямій?

ІІІ. Формулювання теми уроку. Сприйняття й усвідомлення матеріалу.

Теорема формулювання і доведення(слайд 1).

Виконання вправ (слайд 2)

Взаємне розміщення прямої і площини у просторі (слайд 3).

 

 

 

ІV. Осмислення матеріалу

Учні отримують заготовки до малюнків і колективно виконують завдання (Слайд 5,6):

 

Назвіть  дві  площини, які містять пряму  DE. 

 Назвіть пряму,  по якій перетинаються  площини  АЕF  і  SBC.

Назвіть  площину,  яку перетинає пряма  SB. 

Назвіть  дві  площини, які містять пряму  FE. 

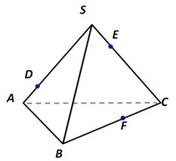 Назвіть пряму,  по якій перетинаються  площини  BDЕ  і  SAC. Назвіть  площину,  яку перетинає  пряма AC. 

 

2. Письмове розв’язування задач (слайд 7).

 

 

 

 

 

V. Підсумок уроку. 

 

Що можна стверджувати про пряму, дві точки якої належать даній площині?

Яке взаємне розміщення прямої і площини?

Як можна задати площину? Оголошення оцінок.

 

  VІ. Домашнє завдання 

1.Точка К не лежить на прямій а. Доведіть, що всі прямі, які проходять через точку К і перетинають пряму а, лежать в одній площині.

 

2.У трикутнику АВС вершини А,В і середина сторони АС лежать у площині β. Доведіть, що всі сторони трикутника лежать у площині β.

 

3.Квадрати ABCD і АВC1D1 не лежать в одній площині. Точки М і N – середини відрізків СВ і А D1 відповідно. Побудуйте точку перетину: Прямої DМ із площиною квадрата АВC1D1 ; Прямої C1N із площиною квадрата ABCD.

 

 

 

 

 

Навчальні тести дозволяють за порівняно короткий час отримати (і викладачу, і учневі) відомості про ступінь упевненості володіння матеріалом великого розділу курсу. Зручності в застосуванні тестів з вибором правильних відповідей очевидне: охоплення відразу великої теми, швидкість перевірки, можливість оперативного зворотного зв'язку з учнями (відповідь невірний - шукайте вірний; дивитися, де помилка; повторити матеріал, до якого ставиться питання); нарешті, високий ступінь об'єктивності. Головна спрямованість тестів - виявити можливі пробіли в кожного учня, допомогти їх заповнити. Тестові питання можна використовувати й вибірково, і в поточному навчальному процесі, і навіть без вибору відповідей - просто як задачі.  1. Скільки існує площин, що проходять через дані пряму й крапку в просторі? 

 

(А) 0	(В) нескінченно багато	(Д) 1 або нескінченно багато
(Б) 1	(Г) 0 або нескінченно багато

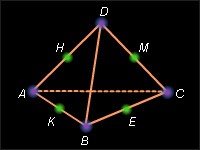
(2–3) Крапки K, E, M, H – середини ребер AB, BC, CD, DA тетраедра ABCD (мал.  1тетраедр АВСД ). 

2.  Яке взаємне розташування прямих KE і MH? 

 

(А)     прямі, перетинаються	що	(В) мимобіжні
(Б) паралельні		(Г) можуть бути прямими, що перетинаються, паралельними й мимобіжними (залежно від виду тетраедра)

3.  Яке взаємне розташування прямих KM і BC? 

 

(А) прямі,що перетинаються	(В) мимобіжні
(Б) паралельні	(Г) можливі всі три випадки (А) – (В)

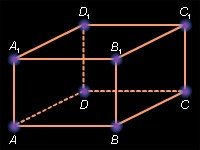
(4–7) Дано прямокутний паралелепіпед ABCDA1B1C1D1 (мал. 2-паралелепіпеда ).  4. Яке взаємне розташування прямих AB1 і BD1?

 

(А) мимобіжні	(В) паралельні		(Д) визначити не можна
(Б)                      прямі,що перетинаються	(Г)      перетинаються паралельні	або

 

5.  Які із прямих b = BB1, c = CC1, d = D1C1 перетинаються із прямою a = AB?

 

(А) тільки b	(В) тільки c і d	(Д) всі три прямі b, c, d
(Б) тільки c	(Г) тільки b і c

 

                                         

Малюнок 1

Малюнок  2

6.  Яке взаємне розташування прямої B1C1 і площини BDA1? 

 

(А) паралельні	(В) перетинаються або паралельні
(Б) перетинаються	(Г) відповідь відмінна від (А) – (В)

7.  Яке взаємне розташування площин BDA1 і B1D1C? 

 

(А) паралельні	(В) перетинаються або паралельні
(Б) перетинаються	(Г) відповідь відмінна від (А) – (В)

8.  У просторі дана пряма a і крапка M. Скільки існує прямих, що проходять через M і паралельних прямій a? 

 

(А) 0	(В) нескінченно багато	(Д) 1 або нескінченно багато
(Б) 1	(Г) 0 або 1

9.  Дано площину й крапку M поза площиною. Скільки існує прямих, що проходять через M і паралельні площини? 

 

(А) 0	(В) нескінченно багато	(Д) 1 або нескінченно багато
(Б) 1	(Г) 0 або нескінченно багато

10.   Дано паралельні пряму a і площину ? Скільки існує площин, що проходять через a і паралельних даній площині? 

 

(А) 0	(В) нескінченно багато	(Д) нескінченно багато
(Б) 1	(Г) 0 або 1

11.   У просторі дані дві паралельні прямі a і b. Скільки існує площин, що проходять через пряму a і паралельних прямій b? 

 

(А) 0	(В) нескінченно багато	(Д) 1 або нескінченно багато
(Б) 1	(Г) 0 або 1

12.   Дано дві площини, що перетинаються і не лежача на них крапка M. Скільки існує прямих, що проходять через M і паралельних площинам ?

 

(А) 0	(В) нескінченно багато	(Д) 0 або нескінченно багато
(Б) 1	(Г) 0 або 1

13.   Дано дві мимобіжні прямі a і b. Скільки існує паралельних площин, одна із яких проходить через a, а інша - через b? 

(А) 0	(В) нескінченно багато	(Д) 0 або нескінченно багато
(Б) 1	(Г) 0 або 1

14.   У просторі дані дві прямі a і b, що перетинаються і крапка M, яка не належить цим прямим. Скільки існує площин, що проходять через M і паралельних прямим a і b?

(А) 0	(В) нескінченно багато	(Д) 0 або нескінченно багато
(Б) 1	(Г) 0 або 1

15.   Крапки A, B і середина M відрізка AB проектують у крапки A1, B1 і M1. Чому дорівнює довжина відрізка MM1, якщо AA1 = 3 см, B1B = 7 см? 

 

(А) 5 см	(В) 2 см	(Д) відповідь відмінна від зазначених
(Б) 4 см	(Г) 5 см або 2 см

 

16.   У просторі дана пряма a і крапка M. Скільки існує площин, що проходять через M і перпендикулярно до прямої a? 

(А) 0	(В) нескінченно багато	(Д) 1 або нескінченно багато
(Б) 1	(Г) 0 або 1

17.   Дано площу  і пряму a, що не належить цій площині. Скільки існує площин, що проходять через пряму a і перпендикулярно площини ? 

(А) 0	(В) нескінченно багато	(Д) 1 або нескінченно багато
(Б) 1	(Г) 0 або 1

18.   Дано три паралельні площини α, β, γ. Відстань між α і β дорівнює 3, відстань між β і γ дорівнює 5. Чому дорівнює відстань між площинами α і γ? 

(А) 2	(В) 8	(Д) 4 або 8
(Б) 4	(Г) 2 або 8

19.   У просторі дані три паралельні прямі a, b, c. Відстань між a і b дорівнює 2, відстань між b і c дорівнює 6. Чому дорівнює відстань x між прямими a і c? 

(А) 0 < x < 6	(В) 2 < x < 8	(Д) 4 < x < 6
(Б) 0 < x < 8	(Г) 4 < x < 8

20.   Відомо, що пряма a паралельна прямій b, а пряма b перетинається із площиною. Яке взаємне розташування прямої a і площини ? 

 

(А)              обов'язково перетинаються	(В) перетинаються або паралельні (тобто можуть і перетинатися, і бути паралельними)
(Б)               обов'язково паралельні	(Г) відповідь відмінна від (А) – (В)

21.   Відомо, що пряма a паралельна прямій b, а пряма b паралельна прямій c. Яке взаємне розташування прямих a і c? 

 

(А)       обов'язково паралельні	(В)           паралельні            або перетинаються	(Д) паралельні або збігаються
(Б)       обов'язково мимобіжні	(Г) паралельні, мимобіжні або перетинаються

22.   Відомо, що пряма a паралельна прямій b, а пряма b паралельна площині. Яке взаємне розташування прямої a і площини ? 

 

(А) обов'язково паралельні	(В) паралельні або перетинаються
(Б) обов'язково перетинаються	(Г) відповідь відмінна від (А) – (В)

23.   Відомо, що площина  паралельна прямій, а пряма  паралельна площині, відмінної від даної площини. Яке взаємне розташування площин ? 

 

(А) обов'язково паралельні	(В) паралельні або перетинаються
(Б) обов'язково перетинаються	(Г) відповідь відмінна від (А) – (В)

24.   Дано три різні прямі a, b і c. Відомо, що a мимобіжна з b, a b перетинається із прямою  c. Яке взаємне розташування прямих a і c? 

 

(А)             обов'язково мимобіжні	(В) мимобіжні, перетинаються або паралельні	(Д) відповідь відмінна від зазначених
(Б)       мимобіжні             або перетинаються	(Г)         мимобіжні         або паралельні

25.   Дано дві прямі a і b, що перетинаються і крапка M, яка не належить даним прямим. Скільки існує площин, що проходять через M і паралельних прямим a і b? 

 

(А) 0	(В) 0 або 1	(Д) О, 1 або нескінченно багато
(Б) 1	(Г) 0 або 1,2

26.   Дано дві мимобіжні прямі a і b. Скільки існує площин, що проходять через пряму a, перпендикулярних до прямої b? 

 

(А) 0	(В) нескінченно багато	(Д) 0 або нескінченно багато
(Б) 1	(Г) 0 або 1

27.   Дано три попарно перехресні прямі a, b і c. Скільки існує прямих, що перетинають всі ці три прямі? 

 

(А) 0	(В) нескінчена кількість	(Д) 1або  нескінчена кількість
(Б) 1	(Г) 0 або нескінчена кількість

28.   На ребрах AD, AB і CD тетраедра ABCD довільно взяті крапки K, E, M. Які ребра, крім трьох зазначених, перетинає площина KEM? 

 

(А) AC	(В) BD	(Д) визначити не можна
(Б) BC	(Г) жодної

29.   Які з наступних фігур можна одержати як паралельну проекцію куба:  I – ромб (не квадрат), II – правильний 5-кутник, III – правильний 6-кутник? 

 

(А) тільки фігуру I	(В) фігури II і III	(Д) всі три фігури
(Б) фігури I і II	(Г) фігури I і III

 

 

 

 

 

1.       Чому мольберт стоїть на трьох ніжках? А чи буде стояти на двох? Відповідь обґрунтуйте.(рис.1) 

 

 

 

 

 

 

 

2.       Ви – пішохід і вам потрібно перейти дорогу по найкоротшому шляху. Зобразіть на малюнку ваш шлях і поясніть, чому цей шлях найкоротший?

 

3.       Прут має декілька точок дотику до поверхні вимірювальної плити, тобто він «нерівний». Що треба зробити, щоб отримати найбільшу довжину прута?

 

4.       Наведіть приклади паралельних площин в конструкції системного блока.

 

5.       Уявіть, що стіл – це площина, а офісна техніка, зображена на рис.2 – неплоскі геометричні фігури. Зобразіть схематично цей малюнок і позначте вершини даних геометричних фігур. За допомогою символів запишіть:

− які точки належать площині?

− які точки не належать площині?

− по яким прямим перетинається площина з многогранниками?

 

 

 

 

 

 

 

       

 

                                           

                                           

6.       До соціальної аптеки від лікарні, яка знаходиться на паралельній вулиці, відстань 500 м. На відстані 400 м від лікарні, по цій самій вулиці знаходиться ЖЕК. Обчисліть відстань від соціальної аптеки до ЖЕКа.

 

7.       Присадибна ділянка має форму прямокутного трикутника АВС з катетами АВ=60 м і АС=80 м. На якій відстані від вершини А повинна проходити паралельна катету межа, яка розділяє   ділянку на дві рівновеликі частини?

 

7.       Як правильно поклеїти шпалери на стіну (рис.3)? 

Назвіть ознаку, яка тут використовується. Відповідь  обґрунтуйте. 

 

 

 

 

                                           

8.       Яким є розміщення картин на стіні відносно стелі (рис.4)? 

Назвіть ознаку, яка тут використовується.

 

 

 

 

 

 

 

 

 

9.       Як розташовані столові прибори при сервіруванні відносно серветок (рис.5)? 

Чи паралельні ложка і ніж? Яка ознака тут виконується?

 

 

 

 

 

 

 

 

 

 

 

 

11. При приготуванні нарізки з овочів, м’яса, сиру і ковбаси, щоб шматочки були однаковими слід різати прямими смужками (рис.6). Які ці прямі? Яка ознака тут виконується?

 

 

 

 

 

 

 

Урок 22

Тема уроку. Тематичне оцінювання.

Мета уроку: перевірка навчальних досягнень учнів з теми «Паралельність прямих і площин у просторі».

Хід уроку

При оцінюванні виконання тестів враховуються тільки ті шість із виконаних завдань, яким відповідає найбільша кількість балів.

Тест «Паралельність прямих і площин»

Мета даного тесту — перевірити, чи вміє учень:  зображати та знаходити на малюнках прямі, що перетинають площину і паралельні їй; розв'язувати задачі, використовуючи ознаку паралельності прямої і площини; зображати та знаходити на малюнках паралельні площини і площини, що перетинаються;  розв'язувати задачі на взаємне розміщення площин, використовуючи відповідні властивості та ознаки.

Варіант 1 

І рівень

1. 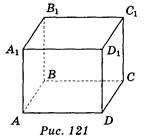  Дано зображення прямокутного паралелепіпеда (рис. 121). Яка з вказаних площин паралельна прямій СЛ? (1 бал)  a) AA1D;      б) ABB1;      в) ВВ1D1;       г) AD1C .

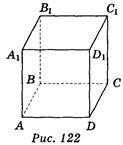
2.   Дано зображення куба ABCDA1B1C1D1 (рис. 122). Яка з вказаних площин паралельна площині BDA1 ? (1 бал)  а) В1D1А;     б) АСВ1;       в) А1С1D1;       г) В1D1С .

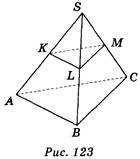
3.   Точки К, L, М — середини ребер SA, SB, SC тетраедра SABC

(рис. 123). Яке взаємне розміщення площин АВС і KLM ? (1 бал) 

а) Перетинаються;  б) збігаються;  в) паралельні; г) визначити неможливо.

                                                                                              

 

II рівень

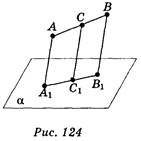
1.      Відрізок АВ не перетинає площину α, С — середина відрізка АВ. Через точки А, В, С проведені паралельні прямі, які перетинають площину а відповідно в точках А1, В1, С1. (рис. 124). Знайдіть АА1, якщо ВВ1 = 4 cm; CC1 = 3 см. (1 бал)  а) 1 см; б) 2 см;    в) 3 см;    г) 4 см.

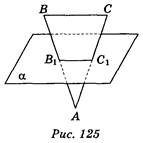
2.      Площина α перетинає сторони АВ і AC трикутника АВС відповідно в точках В1 і С1, ВС || α (рис. 125). Знайдіть ВС, якщо

В1С1 = 1 см, ВВ1 : В1А = 3:1. (1 бал)

а) 1 см;   б) 2 см;   в) 3 см;   г) 4 см,

3.      Дано площину α і точку А поза нею. Скільки існує різних прямих, які проходять через точку А і паралельні α? (1 бал) 

а) Одна; б) жодної; в) дві;  г) безліч.

 

 

III рівень

1.  Точки К, L, М, N є серединами відповідно ребер SA, ВА, ВС, SC тетраедра SABC. Знайдіть периметр чотирикутника KLMN, якщо АС = т , SB = п. (2 бали)

m+n

        а) 2т;          6) 2п;           в) т + п ;         г)     2     . 

2.  У просторі дано дві паралельні прямі а і b, а також точку А, що не належить їм. Скільки існує площин, які проходять через точку А і паралельні прямим а і b? (2 бали)  а) Одна;   б) жодної;    в) дві;     г) безліч.

3.  Які з вказаних фігур можуть бути паралельною проекцією трапеції? (2 бали) 

а) Квадрат;  б) трапеція;   в) ромб;    г) трикутник.

 

IV рівень

1.      АВСDА1В1С1D1 — куб, К — середина ребра СС1. Визначити число сторін перерізу куба площиною, яка проходить через точки В, К, А. (3 бали) 

а) 3;    б) 4; в) 5;   г) 6.

2.      Яку фігуру утворюють усі відрізки, що сполучають будь-які точки двох мимобіжних відрізків? (3 бали) 

а) Чотирикутник;   б) площину; в) тетраедр;  г) відрізок.

3.      ABCD — квадрат зі стороною 6 см. Точка S віддалена від кожної вершини квадрата на 7 см. Знайдіть відстані від середини відрізка SA до середин сторін квадрата. (3 бали)  а) 2,5 см; б) 3,5 см; в) 4,5 см;  г) 5,5 см.

Варіант 2

 

І рівень 

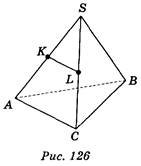
1.  Дано зображення тетраедра SABC (рис. 126). Точки К, L — середини ребер SA і SB. Яка

з вказаних площин паралельна прямій KL? (1 бал)

a) 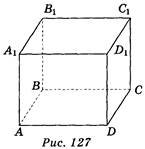  SAC; б) SAB;     в) SBC;   г) АВС.

 

2.  Дано зображення прямокутного паралелепіпеда ABCDA1B1C1D1 (рис. 127). Яка із вказаних площин паралельна площині АВС? (1

бал) 

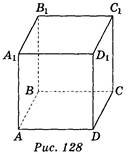
a)   BDC1; б) А1В1С1;     в) BCD;         г) DCC1. 3. Дано зображення куба ABCDA1B1C1D1 (рис. 128). Яке взаємне розміщення площин АСВ1 і

A1C1D ? (1 бал) 

а)                                     Перетинаються;           б)         збігаються;     в)         паралельні;    г)    визначити неможливо.II рівень

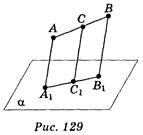
1.     Відрізок АВ не перетинає площину α, С — середина відрізка АВ. Через точки А, В, С проведено паралельні прямі, які перетинають площину а відповідно в точках А1, В1, С1 (рис.

129). Знайдіть СС1, якщо АА1 = 2 см; ВВ1 = 4 см. (1 бал)  а) 4 см; б) 3 см;    в) 2 см;    г) 1 см.

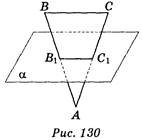
2.     Площина α перетинає сторони АВ і АС

трикутника АВС відповідно в точках В1 і С1, ВС || α (рис. 130). Знайдіть АС, якщо АС1 = 2 см, ВС:В1С1=2:1. (1 бал) а) 1 см; б) 2 см;    в) 3 см;    г) 4 см.

 

 

3.  Дано площину α і точку А поза нею. Скільки існує площин, що проходять через точку А і паралельні α ? (1 бал) 

а) Одна;   б) жодної;    в) дві;    r) безліч.

 

 

III рівень

1.  Точки К, L, М, N є серединами відповідно ребер SA, АС, ВС, BS тетраедра SABC. Знайдіть периметр чотирикутника KLMN, якщо кожне ребро тетраедра дорівнює а. (2 бали) 

а) а;    б) 2а; в) 3а;  г) 4а.

2.  У просторі дано дві мимобіжні прямі а і b і точку А, що не належить їм. Скільки існує площин, які проходять через точку А і паралельні прямим а і b? (2 бали) а) Одна;    б) жодної;    в) дві;   г) безліч.

3.  Які з вказаних фігур можуть бути паралельною проекцією прямокутника? (2 бали) 

а) Квадрат;   б) трапеція;   в) ромб;  г) трикутник.

 

 

IV рівень

1.      ABCDA1B1C1D1 — куб, К — середина ребра СС1. Визначити число сторін перерізу куба площиною, яка проходить через точки А, В1, К. (3 бали) 

а) 3;     б) 4;     в) 5;   r) 6.

2.      Прямі а і b — мимобіжні. Знайдіть геометричне місце точок, утворене прямими, кожна з яких перетинає пряму b і паралельна прямій а. (3 бали)  а) Пряма;    б) площина;   в) тетраедр; г) відрізок.

3.      Три паралельні площини перетинають дві мимобіжні прямі в точках А1, А2, А3 і В1, В2, В3. Відомо, що А1А2 = 4 см, В2В3 = 9 см, А2А3 = В1В2. Знайдіть довжину відрізка А1А3.

(3 бали) 

а) 5 см;    б) 10 см;    в) 13 см;   г) 15 см.

 

 

Відповіді до тестових завдань:

 

 

Рівень	Номер завдання	Варіант 1	Варіант 2
І	1	б	г
	2	г	б
	3	в	в
ІІ	1	б	б
	2	г	г
	3	г	а
ІІІ	1	в	б
	2	а, б	а
	3	б	а, в
IV	1	б	б
	2	в	б
	3	б, г	б

                            

 

 

 

Тема заходу: Паралельність прямих і площин у просторі.

 

Мета: Повторити основні поняття про паралельність прямих і площин у просторі та узагальнити  знання і уміння.

Устаткування: Комп'ютер, проектор, презентація, фотографії стадіонів і шахт.

Хід заходу  

Вступ. Ви знаєте, що в 2012 році в Україні й Польщі пройшов чемпіонат Європи з футболу  - ЄВРО-2012. Давайте й ми сьогодні на уроці поговоримо про футбол і пограємо у футбол, тільки математичний. 

У футболі є свої правила. Їх встановлює організація - Міжнародна рада футбольних асоціацій, у якому по одному голосу мають представники англійської, шотландської і північно - ірландської футбольних організацій і 4 голоси  ФІФА. Нині чинні правила гри у футбол були прийняті в 1997 році й після цього мало змінювалися. 

Ми також приймемо свої правила гри в математичний футбол. У нас буде дві команди по 11 чоловік. Назвемо їх «Шахтар» і «Металіст». Інші учні будуть запасними гравцями. У кожної команди буде капітан, воротар і захисники. Якщо команда відповістить на запитання, виходить, вона забила гол. У цьому випадку команда одержить символічний м'яч. Гра буде складатися із двох таймів. У ході гри не можна порушувати дисципліну, викрикувати з місця, ображати суперників. При порушенні будуть застосовуватися штрафні санкції - призначати пенальті. 

До речі, зона ЄВРО-2012 оголошена зоною вільної від паління. Давайте й ми підтримаємо це правило. І той, хто палить, кине цю шкідливу звичку.      Отже, перед грою проводиться розминка, проведемо її і ми.

 

Розминка

Як можуть розташовуватися прямі в просторі?   

1)    Які прямі називаються паралельними?

2)    Дати визначення прямих,що перетинаються.

3)    Які прямі називаються мимобіжними?

4)    На малюнках назвіть паралельні, мимобіжні та прямі, що перетинаються (Слайд №5)

5)     

 

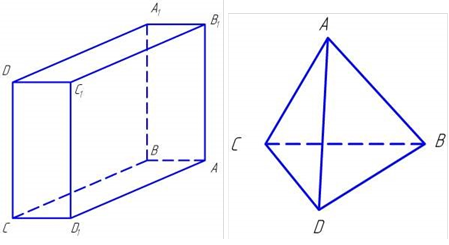
6)    На фотографії стадіону  назвіть паралельні, мимобіжні та прямі, що перетинаються. (Слайд № 6)

 

 

Стадіон «Металіст» у Харкові.

7).(Слайд №7) На знімку шахти знайдіть всі випадки взаємного розташування прямих у просторі:  паралельні, мимобіжні та прямі, що перетинаються.

 

1 тайм.

Граємо у воріт команди «Металіст».      (Слайд №8)

Тест №1. Пряма  а не лежить у площині квадрата АВС і паралельна його стороні АВ. Якому з відрізків паралельна дана пряма?

А) СD;                Б) АD;                В) АС;                  Г) ВD.

 

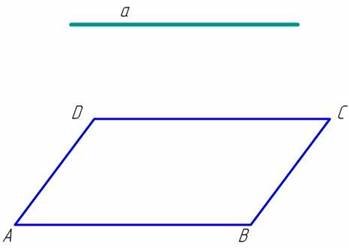
Граємо у воріт команди «Шахтар». (Слайд №9)

Тест №2. Пряма  в  не лежить у площині квадрата КМLN і паралельна його стороні М L. Якому з відрізків паралельна дана пряма?

А) NМ;                Б) ДО N;                В)КМ;                  Г)ДО L.

 

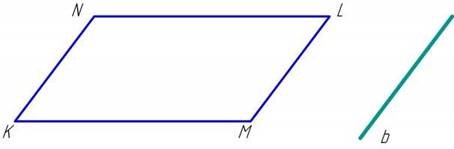
Граємо у воріт команди «Металіст».      

Сформулюйте основну властивість паралельних прямих у просторі. 

(Слайд № 10)

Через крапку, що не лежить на прямій, у просторі можна провести пряму, паралельну даній прямій, і притім тільки одну.

 

 

 

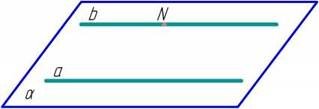
Граємо у воріт команди «Шахтар».

Сформулюйте ознаку паралельності прямих.

(Слайд № 11)

Дві прямі, паралельні третій прямій, паралельні між собою. Граємо на середині поля.

Задача №1. (Слайди № 12, 13)

МК – середня лінія бічної грані АА₁D₁D правильної чотирикутної усіченої піраміди  АВСDА₁У₁С₁D_1. Довести, що МК || ВР.

 

 

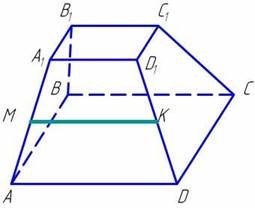
Доведення.

Грань АА₁D₁D правильної чотирикутної усіченої  піраміди  АВСDА₁У₁С₁D_1. є рівнобокою трапецією.

МК || АD - тому що середня лінія трапеції паралельна основі трапеції. У основі піраміди лежить квадрат.

А D || ВР - як протилежні сторони квадрата. Отже, за ознакою паралельності прямих МК || ВР. Що й було потрібно довести.

(Задачу розібрати спочатку усно, потім показати рішення на екрані, з екрана записати в зошит.)

Граємо у воріт команди «Металіст».      

Що називається відстанню від крапки до прямій?

 

(Слайд №14) Грає захисник команди «Шахтар».

Задача №2 (Слайд № 15) Знайти відстань від крапки А до прямих ВР, DС, А₁D_1, якщо лінійні виміри паралелепіпеда рівні 3, 4, 5см. 

 

 

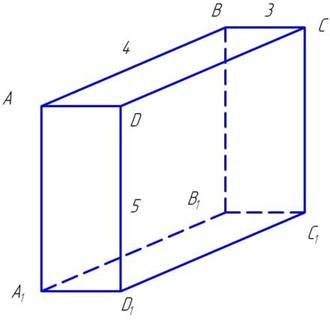
Граємо у воріт команди «Шахтар».

Що називається відстанню між паралельними прямими?

 

 

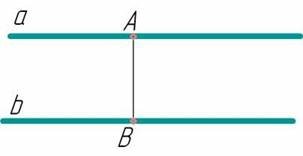
(Слайд № 16) Грає захисник команди «Металіст».

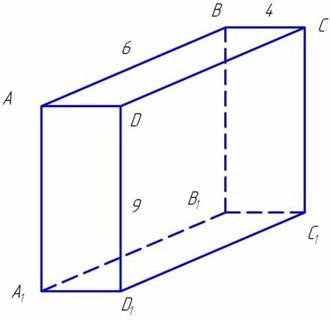
(Слайд № 17)

Задача №3 Знайти відстань між паралельними ребрами прямокутного паралелепіпеда, якщо його виміри рівні 4, 6, 9 см.

 

Закінчився перший тайм. Підведемо підсумок. Команди підраховують отримані м'ячі, переможницею в 1 таймі вважається та команда, у якої більше м'ячів.

2 тайм. (Команди задають питання один одному)Граємо у воріт команди «Металіст».  

1.Яке взаємне розташування прямої і площини в просторі?

(Слайд № 18)

1)    Пряма а лежить у площині _α.

2)    Пряма а перетинає площина _α.

3)    Пряма а паралельна площини _α.

(Слайди № 19, 20)

2. На знімках знайдіть всі випадки взаємного розташування       прямої і площини в просторі.

 

 

 

 

Стадіон «Вісла» у Кракові, Польща.

 

 

    Граємо у воріт команди «Шахтар».

1. У чому полягає ознака паралельності прямій і площині?

(Слайд № 21)

Якщо пряма, що не лежить у площині, паралельна якій-небудь прямій, що лежить у цій площині, то вона паралельна й самої площини. Граємо у воріт команди «Металіст».      

2.Яке взаємне розташування двох площин у просторі?

(Слайд № 22)

1)    Дві площини перетинаються.

2)    Дві площини паралельні. (Слайди № 23, 24, 25)

 На знімках знайдіть всі випадки взаємного розташування        площин у просторі.

 

 

 

НСК «Олімпійський» у Києві.

 

Стадіон у Донецьку «Донбас Арена».

 

 Граємо у воріт команди «Шахтар».

У чому полягає ознака паралельності площин.

(Слайд № 26)

Якщо дві пересічні прямі однієї площини відповідно паралельні двом пересічним прямим іншої площини, то ці площини паралельні.

Грає капітан команди «Шахтар»

Задача №4.

(Слайди №27, 28)

 

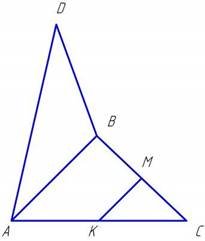
Трикутник АВС не лежить в одній площині із трикутником АВД і має з ним спільну сторону АВ. Довести, що середня лінія КМ трикутника АВС паралельна площини  трикутника АВД.

Рішення. (Слайд)

У трикутнику АВС середня лінія паралельна основі АВ. Пряма АВ лежить у площині трикутника АВД. Отже, з ознаки паралельності прямої  і площини КМ ||(АВД).

 

Грає капітан команди «Металіст».

Задача №5.

(Слайди № 29, 30) 

 

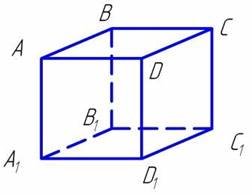
У кубі довести паралельність граней АВСД і А₁В₁С₁D₁.

Рішення.

АВ || А₁В₁, АD || А₁D₁  як протилежні сторони квадрата. АВ і АD,  А₁В₁ і А₁D₁ –прямі, що перетинаються.  Отже, за ознакою паралельності площин   грані АВСД і А₁В₁С₁D₁ паралельні.

(Слайд № 31)

Додаткова задача №6.

Паралельні площини _α і _β перетинають сторону АВ кута ВАС у крапках М і М₁, а сторону АС відповідно в крапках К и К₁. Знайдіть довжину відрізка МК якщо:

1) АМ = 12см, А М₁ = 18см, М₁К₁ = 5,4см;

 

Закінчився другий тайм, команди підраховують загальну кількість м'ячів, визначається переможець.

 

 

 

 

 

 

 

 

 

 

 

1.   Погорелов О.В. Геометрія, 10-11 клас -  Київ: Освіта, 2015.

 

2.   Клопський В.М Геометрія, 9 клас – Київ: Радянська школа, 2014.

 

3.   Науково-методичний збірник “Новітні технології навчання” Науковометодичний центр вищої освіти.

 

4.   Журнали «Математика в школі»,№6,  2016, №4, 2017, №7, 2017.

 

5.   Капіносов А.М. Геометрія, 10 клас, Дидактичні матеріали для різнорівневого навчання.

 

6.   І.М. Смирнов Збірник усних  задач і вправ для геометрії учнів 10-11 класів

- Москва:Нивериум 2015.

 

7.   О.Н.Земляков Геометрія в 10 класі: Методичні рекомендації – Київ Освіта 2014.

 

8.   Інтернет ресурси:

-http://metodportal.net

-   http://osvita.ua

-   http://llacaountr.com

-   http://www.formula.com.