Науково - дослідницька робота на тему : « Теорема Піфагора. Нестандартні доведення»

Немирівський навчально-виховний комплекс

«загальноосвітня школа І-ІІІ ступенів №2 –ліцей»

Немирівської районної ради

Вінницької області

 

 

 

Науково - дослідницька

робота на тему :

 

 

 

Роботу виконала

учениця НВК №2 м. Немирова

Репула Вікторія

Науковий керівник

Учитель математики НВК№2

м. Немирова

Сметанська Юлія Анатоліївна

 

         2008-2009 н.р.

 

ЗМІСТ

1. Так сказав Піфагор
2. Піфагор і його теорема
3. Доведення теореми Піфагора математиками різних століть
4. Нестандартні способи доведення теореми Піфагора
5. Література

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Так сказав Піфагор

1.  Живи з людьми так, щоб твої друзі не стали недругами, а недруги стали друзями.

2.   Твори велике, не обіцяючи великого.

3.   Не заплющуй очей, коли хочеш спати, не проаналізувавши всіх своїх учинків за минулий день.

4.   Тимчасова невдача краще тимчасової удачі.

5.  Не роби нічого ганебного ні в присутності інших, ні таємно.

6. Першим твоїм законом має бути повага до себе самого.

7. Лише неблагородна людина здатна в очі хвалити, а поза очі злословити.

8.  Роби лиш те, що в майбутньому не засмутить тебе.

9.   Усе впорядковується відповідно до чисел

 

 

 

 

 

 

 

Піфагор і його теорема.

Мабуть, найпопулярнішою з усіх теорем є теорема Піфагора. Причинами такої популярності є простота, краса, значення. Справді, теорема Піфагора проста, але не очевидна. Це поєднання двох суперечностей і надає їй особливої привабливості. Теорема Піфагора має велике значення: вона використовується дуже часто, той факт, що існує близько 500 різних доведень цієї теореми, свідчить про велику кількість її реальних реалізацій.

З ім'ям Піфагора пов'язана, мабуть, найбільша кількість різних цікавих подій та легенд. Навіть саме ім'я цієї видатної людини незвичайне, бо воно буквально означає «Той, про кого сповістила Піфія», отже, народження Піфагора було передбачено заздалегідь.

Легендарною особою Піфагора вважали вже у стародавні часи — у 306 р. до н. е. йому, як найрозумнішому з греків, встановили пам'ятник на римському форумі перед коміцієм (місцем, де відбувалися народні збори). Він простояв там до початку правління Сулли. А вперше слава при­йшла до Піфагора, коли він був ще ефебом (юнаком). Коли йому виповнилося вісімнадцять років, він, за звичаєм багатьох молодих людей свого часу, почав подорожувати і, перш за все, поїхав до Мілету , щоб зустрітися з Фалесом. Фалес зустрів його ласкаво, щиро поділився своїми знаннями, але, жаліючись на старість і слабке здоров'я, порадив їхати до Єгипту, щоб ще повчитися у єгипетських жерців. Він також сказав, що ні від природи, ні внаслідок навчання не має такої вдачі, яку він бачить у Піфагора. Тому, спілкуючись з уславленими жерцями, Піфагор може стати найбільш близьким до богів і найрозумнішим серед людей.

 Відкриття теореми оточене ореолом красивих легенд. Грецький філософ Прокл (410-485), коментуючи першу книгу  «Начал» Евкліда, пише: «Якщо послухати тих, хто повторює давні легенди, то доводиться сказати, що це теорема походить від Піфагора; розповідають, що він на честь цього відкриття приніс у жертву бика». Дехто розповідає, що він приніс у жертву не одного бика, а цілу сотню. На цю тему  німецький поет Альберт Шаміссо написав вірш, який в перекладі Наталії Теренової звучить так:

Во мгле веков пред нашим взором

Блеснула истина .Она ,

Как теорема Піфагора,

До наших дней еще верна.

С тех пор быки тривожно дышат,

Они, кляня дары богов,

О новой истине услышав,

Ужасный поднимают рев.

Найдя разгадку, мудрый старец

Был благодарен небесам;

Он сто Быков велел зажарить

И в жертву принести богам.

Их старца имя потрясает,

Их истины лучи слепят:

И, новой жертвы ожидая,

Быки, зажмурившись ,дрожат.

Про життя Піфагора майже не збереглося відомостей. Є підстави вважати, ще він народився близько 580-500р.до н. е. на о. Самос . З цієї причини його називають Піфагором Самоським. Батьком Піфагора був Мнесарх, різьбяр по коштовних каменях. Ім’я матері невідоме.

У молоді роки Піфагор виїхав до Єгипту вивчати науки і пробув там майже 22 роки. Під час завоювання Єгипту Персією , його захопили в полон і вивезли до Вавилону де він прожив близько 12 років. У Вавилоні  Піфагор вивчив , крім математики , астрологію й астрономію.

Здобувши широкі знання в галузі природничих наук (у тому числі й математичних),Піфагор повернувся на о.Самос, де мав намір створити свою школу.  Але в своєму рідному місті Піфагор не знайшов однодумців і переселився до м. Кротона, де організував гурток , який пізніше дістав назву Піфагорійської школи. Організація піфагорійців була таємною, одночасно і філософською школою,  і політичною партією , і релігійним братством. У гурток приймали з великими почестями після випробувань. Кожен, хто приходив у гурток відмовлявся від свого майна й обіцяв зберігати в таємниці ім’я засновника. У цій його «школі» процвітали математика, філософія, астрономія і музика.

Наукові, насамперед математичні, дослідження Піфагора і його школи були органічно пов’язані з філософією. Так ,числам натурального ряду вони надавали надприродного , містичного значення, тому математика в їх філософському трактуванні мала таємничий характер, недоступний, на їх думку , для  людей. Вони висловлювалися так: «Речі - відображення чисел, числа - закон і зв’язок світу, це сила ,що керує богами і смертними.....»

Піфагор вважав , що число  5 символізує колір, 6- холод, 7 – розум, здоров’я та світло , 8- кохання, дружбу, 9- постійність, 13,14 були ненависними числами. Піфагорійці розрізняли такі види чисел : числа добрі - непарні числа, числа злі - парні числа, числа  досконалі ,що дорівнюють сумі своїх  дільників , числа дружні – такі з яких кожне дорівнює сумі дільників другого ,але без самого числа ,числа пірамідальні, многокутні тощо.

     Піфагор першим з грецьких математиків знайшов пропорції і найпростіші прогресії. Піфагорійці розрізняли три види пропорції: арифметичну, геометричну і гармонічну. Гармонічними вони називали три числа а ,b, с ,які утворюють арифметичну пропорцію:

                                        

 Наприклад ,числа 3,4 і 6 є гармонічними ,бо   .

Піфагор установив, що коли довжини струн музичного інструмента відносяться як 6:4:3,то в звучанні вони дають правильний гармонійний акорд. Назву «гармонічна»пропорція , очевидно ,взято звідси.

Піфагорійці займались також теорією музики. Вони помітили, що коли струну або сопілку вкоротити вдвоє, то їх звук стане вищий на октаву. Зменшення їх довжини у відношенні 3 : 2 дає квінту, а у відношенні 4:3 — кварту. Звідси був зроблений висновок, що числа 1, 2, 3, 4 характеризують основні музичні інтервали. Співзвучність тонів, які викликають у нас приємне враження, греки назвали гармонією. Потім ця назва перейшла й на інші явища в природі і в людському житті: гармонією називають усе, де є згода, злагодженість, усе, що дає задоволення нашому зору, слуху або думці

Таку саму гармонію Піфагор вбачав і в рухах небесних світил. Провідною думкою філософії піфагорійців було твердження, що число є суть усіх речей і що Всесвіт є гармонійна система речей і їх відношень.

Про Піфагора і його школу відомо дуже мало; не можна навіть сказати, які відкриття належать самому Піфагору, а які — його учням. Піфагорові приписують систематичне запровадження в геометрію доведень, створення вчення про подібність, побудову деяких многокутників тощо.

Піфагорійці багато займались арифметикою цілих чисел, проте у вченні піфагорійців про числа було багато містичного.

Але найбільшим досягненням піфагорійців треба вважати теорему, названу піфагоровою (точніше, не так саму теорему, як ті висновки, які вони зробили з неї).

Вже дуже давно, ще за два тисячоліття до нашої ери, єгипетські землеміри і будівельники будували прямі кути, натягуючи на кілках, забитих у землю, шнур у формі трикутника з сторонами 3, 4, 5 одиниць (так званий «єгипетський» трикутник). Тут маємо  3²+4²=5², причому кут, який лежить проти найбільшої сторони, прямий.

Можна припустити  , що найпростіший з трикутників ,так званий єгипетський зі сторонами 3,4,5 став відомим Піфагору після подорожі країнами сходу (Єгипет ,Вавилон). Вважають ,що Піфагор знайшов правило (теорему Піфагора) для знаходження сторін такого трикутника, яке можна подати формулою : х²  + у²=z². 

Мабуть, роздумуючи над цим цікавим фактом, Піфагор почав шукати й інші прямокутні трикутники з цілочисловими сторонами. Та коли він узяв за катети відрізки завдовжки по одиниці, то побачив, що довжину гіпотенузи не вдається визначити цілим числом.

Це відкриття було великим ударом по його філософському вченню, яке зводилось до того, що кожну величину, отже, і довжину, можна подати цілим числом. З другого боку, це було надзвичайно важливе відкриття в математиці: Піфагор відкрив новий вид чисел — так звані ірраціональні числа, тобто такі, які не можна подати як відношення двох цілих чисел. Розглядаючи прямокутний трикутник з одиничними катетами, Піфагор і прийшов до одного з цих чисел, а саме .

Якось  дивно читати, що про теорему, яку названо ім'ям Піфагора, він сам довідався тільки під час своїх мандрів по єгипетській і вавілонській землях! Проте в тому, що цій теоремі надано ім'я Піфагора, є й деяка рація, бо Піфагор та його учні багато займалися нею. Дехто вважає, що Піфагор перший дав її повноцінне доведення.

Перше строге геометричне доведення теореми Піфагора: Сума площ квадратів, побудованих на двох катетах прямокутного трикутника, дорівнює площі квадрата, побудованого на його гіпотенузі, знаходимо в «Началах» Евкліда. Воно полягає в доведенні того, що висота, опущена з вершини прямого кута на гіпотенузу, розбиває квадрат, побудований на гіпотенузі, на два прямокутники, площі яких дорівнюють площам квадратів, побудованих на катетах. Обернене твердження також правильне: якщо сторони трикутника відповідають піфагорійській умові:

                                     a²+b² =c²

то трикутник буде прямокутним з прямим кутом, що лежить проти сторони с.

Піфагорійці знали, що сума внутрішніх кутів трикутника дорівнює 180 градусів, що на площині розмістити 4 квадрати,6 правильних трикутників,3 правильні шестикутники , що мають спільну вершину і не накладаються один на одного. За свідченням істориків, піфагорійці вміли будувати 5 видів правильних  многогранників , які ми нині вивчаємо.

Школа Піфагора зробила геометрію наукою. Характерною рисою методики Піфагора  було поєднання геометрії з арифметикою.

За філософським поглядом Піфагор був ідеалістом , захисником інтересів рабовласницької аристократії. У кінці 5 століття до нашої ери в Греції і в її колоніях прокотилася хвиля демократичного руху . Перемога демократія і в Кротоні. Школа Піфагора діяла відокремлено від решти громадянства. Ця її таємничість і гострі виступи проти демократії породжували  ненависть до всіх піфагорійців. Будинок школи був розгромлений і сам Піфагор мусив утекти, Піфагор зі своїми учнями мусив переїхати з Кротона до Тарента ,а потім до Метапонта. У цьому місці 80-річний філософ загинув. Коли він помер, перестала існувати і його школа: учні Піфагора розбрелися по Греції і почали поширювати вчення свого вчителя по всій країні. Так таємне стало явним.

Важливість теореми Піфагора ілюструє такий цікавий факт.

Наприкінці XIX ст. було відкрито на Марсі «канали», які тривалий час вважалися штучними. Для налагодження зв'язку з марсіянами запропонували на величезному просторі Західної Сибірської низини побудувати гігантську геометричну фігуру, яка б світилася, — рисунок теореми Піфагора, бо вважали, що ця теорема справедлива скрізь і що жителі будь-якої планети повинні зрозуміти такий сигнал. Передбачали, що, побачивши це зображення, марсіяни зроблять висновок, що на Землі живуть розумні істоти, і дадуть відповідь також мовою математики. Адже математику вважають універсальною мовою Всесвіту!

У 1955 р. в Греції було випущено поштову марку, що ілюструє теорему Піфагора. Дивлячись на неї, можна наочно пересвідчитися в тому, що в прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів.

 

 

 

 

 

 

 

 

 

 

 

 

Доведення теореми Піфагора

математиками різних століть

Теоремою Піфагора займалось багато математиків протягом багатьох століть. У наш час теорему Піфагора доведено більш як 500 способами. Хоча майже в кожному столітті знаходять нові способи доведення , але і зараз у математиків не зникло бажання збільшити їх кількість.

                 ДОВЕДЕННЯ    ЕВКЛІДА

      Ще Евклід у своїх «Началах» наводить вісім способів доведення ,які можна зрозуміти за малюнками:

 

 

 

 

 

 

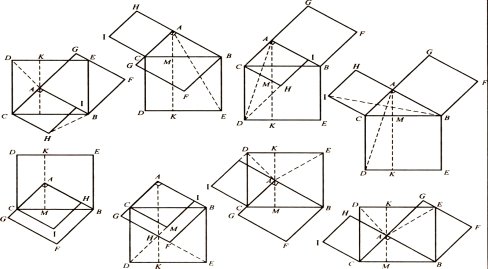
Крім доведень Евкліда ,можна навести ще цікаві математичні доведення з використанням рівновеликих фігур. У всіх цих доведеннях введемо такі позначення:, BC=a,CA=b, AB=c

 

ДОВЕДЕННЯ    НАСРЕДІНА

 

 

 

 

     Δ GAL = Δ ABC,

       LA = CB,

GAL = ABC =CAM,

тому точки L, Α, Μ, Κ лежать на одній прямій. Отримали фігури з рівними площами:

        Аналогічно        .

        Але                   .

Отже, a²=b²+c²

 

 

 

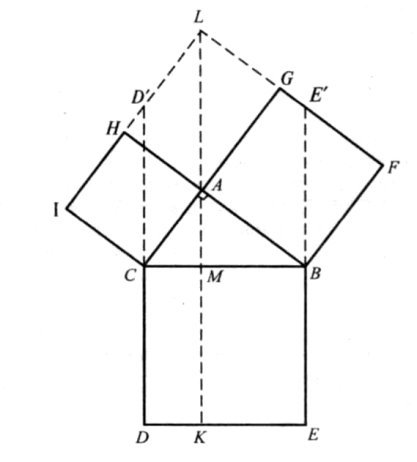
ДОВЕДЕННЯ ГОФМАНА

Перший спосіб

Продовжимо відрізок СD до перетину з продовженням відрізка FL у точці N. Отримаємо фігури з рівними площами:                 

…

Але …                    Отже,   a²=b²+c²

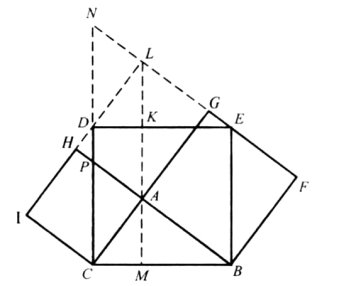
    Другий спосіб 

  Проведемо

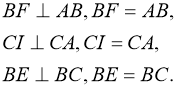
Легко довести ,що точки F,A,I  лежать на одній прямі. Чотирикутники IFAC і FBEC  рівновеликі , оскільки  ∆СBE=∆ABF і…. Віднявши від площ обох чотирикутників площу спільного трикутника ABC,матимем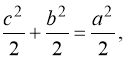о:тобто

ДОВЕДЕННЯ ТЕМПЕЛЬГОФА

   Легко довести ,що Δ LDE= Δ ABC, Δ AGH=ABC.

Рівними будуть також  чотирикутники  LDCA, FBCI і ABEL,та IHGF і ICBF.Отже, шестикутники  ICBFGH і ACDLEB рівноскладені .Вони мають спільний трикутник ABC ,а також   Δ AGH= Δ LDE. A це означає   що   

                                     ДОВЕДЕННЯ  РЕНАНА

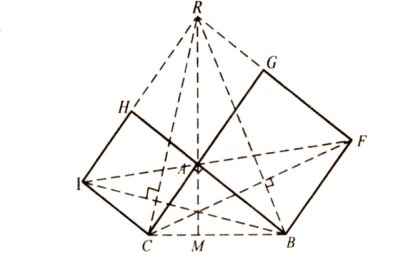  Оскільки ΔHRA= ΔABC, то RA=BC. З рівностей ΔІВС= ΔCAR, ΔFBC= ΔBAR випливає, що RA………….є висота трикутника BCR, тому вони перетинаються в одній точці .

,

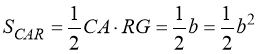
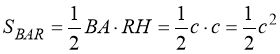
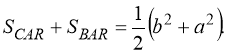Тому                                                     ,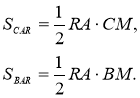

                ,

                                 Отже,  

                 Давньоіндійське   доведення

У книзі «Вінок знання» індійській математик Бхаскара наводить доведення теореми Піфагора у вигляді креслення з підписом «Дивись!»

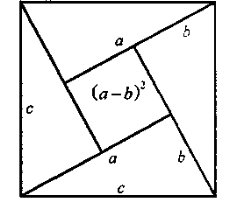Як дістати з креслення Бхаскари доведення теореми Піфагора?

Площа квадрата, побудованого на гіпотенузі с трикутника, дорівнює сумі площ чотирьох прямокутних трикутників і квадрата, довжина сторони  якого а-b.

Тобто

               Отже,  с² = а²+b².           

 

Давньокитайське  доведення

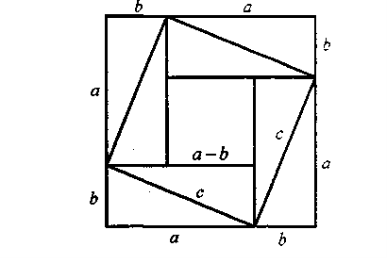У коментарі до задачі з «Трактату про мірну віху» є посилання на креслення, де квадрат, побудований на сумі катетів а і b прямокутного трикутника, подано як суму площ інших фігур.

Як дістати з цього креслення  доведення теореми Піфагора?

Тому

 Доведення теореми Піфагора в малюнках

Ряд доведень теореми Піфагора можна показати за допомогою дотепних рисунків:

 

 

 

 

 

 

 

 

Теорема Піфагора була іноді темою учнівських жартів; її зображали у вигляді різних смішних фігурок :

А в Росії рисунок до теореми Піфагора для випадку рівнобедреного трикутника учні називали   «піфагорійськими штанами»

 

У Франції  і Німеччині теорему Піфагора називали «ослячим мостом» (якщо учень не знав теореми то це був справжній осел)

Нестандартні  способи доведення теореми Піфагора

Відомо, що теорема Піфагора є однією з найважливіших у геометрії. Адже спираючись на той факт, що квадрат гіпотенузи прямокутного трикутника дорівнює сумі квадратів катетів, ми розв'язуємо і доводимо багато задач.

В шкільному курсі геометрії пропонується доведення теореми Піфагора тільки через косинус кута.

Розглянемо деякі інші способи доведення теореми Піфагора, під час яких використовуються  різні теми шкільного курсу геометрії.

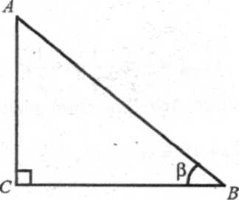
І СПОСІБ. (Тема «Основні тригонометричні тотожності».)

 Довести теорему Піфагора, використовуючи основну тригонометричну тотожність.

Дано: ∆АВС (C = 90°).

Довести: АВ² = АС² + ВС².

Доведення

У трикутнику ABC (C = 90°) АС та ВС - катети, АВ - гіпотенуза.

Відомо, що:

sin В =,    cos В =

звідки маємо:

AC = ABsinB, BC = ABcosB.

В обох рівностях піднесемо обидві частини до квадрата, отримаємо:

АС² = АВ² sin² В , ВС² = АВ² cos² В.

 Додамо почленно ці рівності:

 АС² + ВС² = АВ² sin² В+ АВ² cos² В ,

 АС² + ВС² = АВ² (sin² В+cos² В).

Використовуючи основну тригонометричну тожність

 sin² α+cos² α = 1, маємо:

AC² + BC² = АВ², що і потрібно було довести.

Як бачимо, в цьому доведенні треба знати означення синуса і косинуса прямокутного трикутника а також формулу sin² α+cos² α = 1.

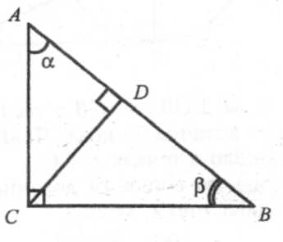
ІІ СПОСІБ(Тема «Подібність трикутників».)

 Довести теорему Піфагора, використовуючи  властивість подібних трикутників.

Дано: ∆АВС (C = 90°),

A =α, B = β.

Довести: АВ²=АС²+ВС².

 

Доведення

    Проведемо CD ┴АВ . Отримали два прямокутні трикутники:

ACD (D = 90°) і BDC (D = 90°). Знайдемо кути цих трикутників.

У трикутнику ACD (D = 90°): A = α; оскільки B= β, α+β = 90°, ADC = 90°,to

DCA =90°-A = 90°- α = β.

У трикутників ABC і ACD кути рівні, а це означає, що ΔABC~ΔACD.

 За властивістю подібних трикутників їх сторони пропорційні, тобто:

AB: AC = AC:AD,

                                    АС² = АВ · AD   (1)

У трикутнику CBD (D = 90°): B = β; ACB = = 90°-B= 90-β = α.

У трикутників ABC і CBD кути рівні, а це означає, що ΔABC~ΔCBD; отже, сторони цих три­кутників пропорційні, тобто:

АВ :СВ = СВ: DB,

      СВ² = АВ · DB .(2)

Додамо почленно рівності (1) і (2):

AC² +СВ² = AB·AD+AB·DB ,

AC² +СВ² = AB·(AD+DB) ,

АС²+СВ²=АВ · АВ,

                        АС² + СВ² = АВ²,

 що і потрібно було довести.

 

У доведенні використовується ознака подібності трикутників за двома кутами і той факт, що у подібних трикутниках відповідні сторони пропорційні.

ІІІ СПОСІБ (Тема «Подібність трикутників».)

 Довести теорему Піфагора, використовуючи  властивість про відношення площ  подібних трикутників.

Доведення

Нехай дано трикутник ABC (C = 90°).

Доведемо, що

                 AB²=CB² + AC².

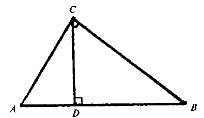У прямокутному трикутнику АВС з прямим кутом С і висотою CD позначимо S₁=S_ADC, S₂=S_BCD, S₃=S_ABC

Тоді S₁+S₂=S₃

 Оскільки Δ ACD подібний Δ ABC , то

                      .

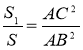З подібності трикутників BCD і ВАС маємо:

                                         '

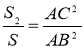Тому АС² + ВС² = AВ².

У доведенні використовується ознака подібності трикутників за двома кутами і той факт, що у подібних трикутниках площі пропорційні квадратам відповідних сторін.

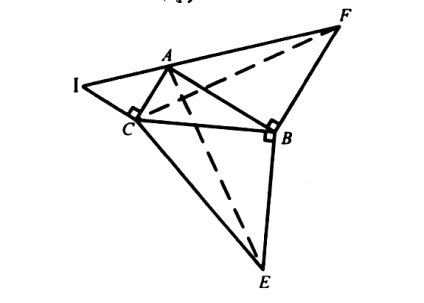
ІV СПОСІБ (Тема «Властивість січної та дотичної, проведених до кола з однієї точки».) Довести теорему Піфагора, використовуючи властивість січної та дотичної, проведених до кола з однієї точки.

Дано: ∆АОВ (B = 90°).

Довести: AO² = ОВ²+АВ².

Доведення

Будуємо коло з центром у точці О і радіусом ОВ. Воно перетне гіпотенузу AO в точці D.

 

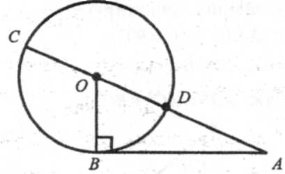
Оскільки АВ ┴ ОВ, де ОВ — радіус, то це означає, що АВ — дотична до кола. Пряма AO є січною і перетинає коло в точках D і С.

За властивістю січної та дотичної, проведених до кола з однієї точки, маємо:

AB²=AD·AC. (3)

Оскільки

AO = OD+AD, АС = АО+ОС = АО+ОВ,

то

AD = AO - OD = АО - ОВ .

  Підставляємо знайдені вирази для AD  та  АС у формулу (3):

АВ² =(АO-OB)(АO+OB),

АВ² = AO² - ОВ²,

АВ² +ОВ² =АО²,

 що і потрібно було довести.

Доведення цікаве тим, що дає змогу побачити, як іноді допоміжні побудови допомагають отримати бажаний результат.

V СПОСІБ (Тема «Площа трапеції».) За даними на малюнку довести теорему Піфагора, а саме, що

c²=a²+b².

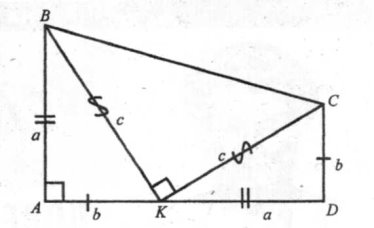
Доведення

На малюнку зображено прямокутну трапецію ABCD з основами CD = b та АВ= a; DA = а + b — висота трапеції.

За формулою площі трапеції маємо:

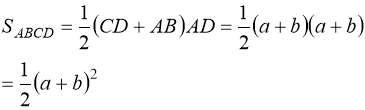        (4)

З іншого боку, трапеція складається з прямокутних трикутників АВК, ВКС, CDK. Тому її пло­ща дорівнює сумі площ цих трикутників, тобто

        

Відомо, що площа прямокутного трикутника до­рівнює половині добутку катетів.

Отже:   

     

       

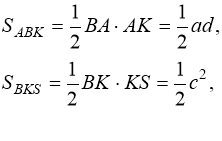
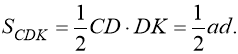
Тоді                     (5)

Прирівняємо праві частини рівностей (4) і (5):

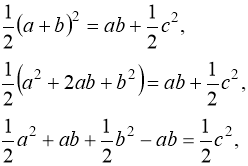
a² +b² =c², що й потрібно було довести.

   Як бачимо, в цьому доведенні використовую те, що:

• у прямокутній трапеції одна бічна сторона є висотою;
• площа фігури дорівнює сумі площ фігур, з яких вона складається;
• площа прямокутного трикутника дорівнює півдобутку катетів;
• квадрат суми двох виразів дорівнює сумі квад­ратів цих виразів і подвоєного їх добутку.

 

 

VІ СПОСІБ. Довести теорему Піфагора, використовуючи формули для обчислення площі трикутника.

Дано: ∆АВС (C = 90°), СА = b, СВ = а, АВ = с.

Довести: с² =а²+b².

Доведення

Впишемо в трикутник  ABC (C = 90°) коло з центром у точці О.

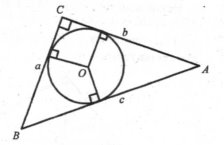
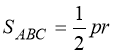Відомо, що S_ABC=ab. З іншого боку,      , де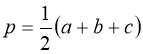— півпериметр трикутника ABC,

r = (a + b-c) - радіус вписаного в прямокутний  трикутник кола.

З двох рівностей для площі трикутника ABC маємо:

         

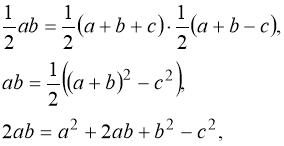
                с²=а²+b²,

 що й потрібно було довести.

VІІ СПОСІБ (Тема «Відстань між точками на коор­динатній площині».) Довести теорему Піфагора методом координат.

Доведення

  Нехай дано трикутник ABC (C = 90°).

Доведемо, що АВ²=АС² + ВС²

 Виберемо систему координат так, щоб вершина С збігалася з початком  відліку, а катети лежали на осях.

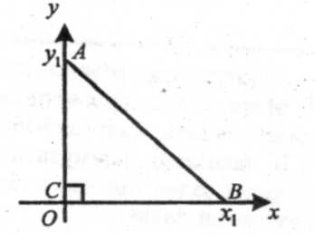
Тоді точка С матиме координати (0; 0), точка В (х₁; 0), точка А (0; у₁). Знайдемо квадрати відстаней між точками А, В, і С :

              

 

                АС²=(0-0)²+(0-у₁)²=у₁²,

                         ВС²=(0-х₁)²+(0-0)²=х₁²,

   звідки

АВ² = AC² +ВС², що і потрібно було довести

 

VІІ СПОСІБ (Тема «Вектори».) Довести теореми Піфагора векторним методом.

Доведення

Нехай дано трикутник ABC (C = 90°).

Доведемо, що

                 AB²=CB² + AC².

 На сторонах трикутника  побудуємо вектори СВ, АС, АВ.

Тоді, АВ = СВ + АС.

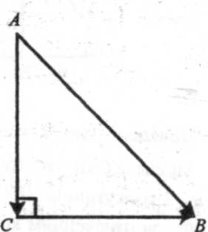
Піднесемо обидві частини останньої рівності до  квадрата:

         (CB+AC)² =AB² ,

СВ² + 2СВ·АС+АС² =АВ² ,

 За умовою CB┴AC, тому СВ·АС = 0,

 СВ² + АС² = АВ², що й потрібно було довести

 

 

 

VІІІ СПОСІБ( наочне доведення )

Якщо вирізати з картону три квадрати .сторони яких дорівнюють сторонам даного трикутника , і покласти два менших квадрати на одну шальку досить чутливих терезів , а на другу шальку – третій, то терези будуть у рівновазі.

 

 

Література

1.Математична хрестоматія. За редакцією О.С.Смогоржевського,

 «Радянська школа» , Київ,!968.

2.В.Литцман. Теорема Піфагора, Москва,  1985

3.С.Сафонюк.Слава Піфагору.

Газета «Математика» №2(350), січень 2006.