Методичні матеріали "Тригонометрія"

1. ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ

Практичне заняття 1

Обчислення значень тригонометричних функцій за допомогою калькулятора і таблиць. Дії з наближеними значеннями чисел.

Мета. Знати значення абсолютної та відносної похибок наближених значень. Уміти виконувати дії з наближеними числами, обчислювати значення тригонометричних функцій за допомогою таблиць та калькулятора.

Література: [ 6], с. 86–100.

Теоретичні відомості

Абсолютною похибкою наближеного значення називається модуль різниці точного і наближеного значень числа.

Відносною похибкою наближеного значення називається відношення абсолют­ної похибки до модуля наближеного значення.

Границею відносної похибки наближеного значення α називається відно­шення границі абсолютної похибки до модуля числа α.

Дії з наближеними числами

1. При додаванні, відніманні наближених значень у результаті залишають стільки десяткових знаків, скільки має дане число з найменшою кількістю десяткових знаків.
2. При множенні і діленні наближених значень у результаті залишають стільки значущих цифр, скільки їх має наближене дане з найменшою кількістю значущих цифр.
3. При піднесенні до степеня в результаті зберігають стільки значущих цифр, скільки їх в основі степеня.
4. При добуванні кореня зберігають стільки значущих цифр, скільки їх в підкореневому виразі.
5. У результаті проміжних дій залишають на одну (запасну) цифру більше, підкреслюючи її. В остаточному результаті запасна цифра відкидається за правилами округлення.

Завдання 1

1. Знайти границю абсолютної похибки таких чисел:

а)

б)

в)

2. Визначити границі відносної похибки наступних чисел:

а)

б)

в)

3. Виконати дії з наближеними числами

а) ;

б) ;

в) ;

г)

Формули переходу від радіанної міри кута до градусної і навпаки

  .

Тригонометричні функції

Синусом числа  а називається ордината точки Р_а одиничного кола, в яку переходить початкова точка Р₀ (1; 0) при повороті навколо центра кола на кут а радіан і позначається sin α.

Косинусом числа α називається абсциса точки Р_а одиничного кола, в яку переходить початкова точка Р_а (1; 0) при повороті навколо центра кола на кут α радіан і позначається cos α.

Тангенсом числа α називається відношення , а котангенсом числа  α – відношення .

Знаки тригонометричних функцій у чвертях

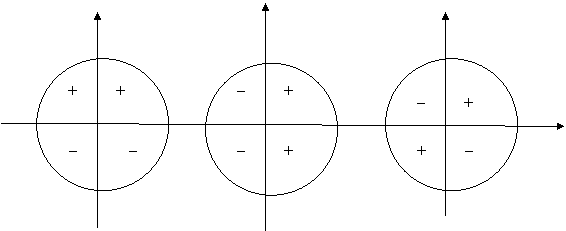         у                  у        у

             sin a       cos a    tga

                     ctga

Рис 1.

Завдання 2

1. Записати в радіанній мірі кути:

а)

б)

в)

2. Подати в градусні мірі кути:

а)

б)

в)

3. Обчислити значення виразів:

а)

б)

в)

Питання для самоконтролю

1. Що називається синусом, косинусом, котангенсом?
2.               При яких значеннях α, sin α, cos α, tg α, ctg α мають зміст?
3.               Що таке радіан?
4.               Яка залежність між градусною і радіанною мірою?