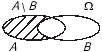Методичні рекомендації

до вивчення теми:

«Елементи теорії ймовірностей і математичної статистики»

в 11 класі загальноосвітньої школи

 

Теорія імовірностей, подібно до інших розділів математики, розвинулася з потреб практики; в абстрактній формі вона відображає закономірності, властиві подіям масового характеру. Ці закономірності відіграють надзвичайно важливу роль у фізиці та інших галузях природознавства, військовій справі, різноманітних технічних дисциплінах, економіці тощо.

Б. В. Гнеденко

АНОТАЦІЯ

Найважливішою метою для кожного вчителя є планування вивчення наступної теми. Елементи теорії ймовірностей і математичної статистики у курсі 11 класу загальноосвітньої школи вивчаються порівняно недавно і є однією з найскладніших для дитячого розуміння тем. Тому надзвичайно важливо спланувати її вивчення так, щоб не налякати дітей складністю й різноманітністю теоретичних основ, формул і теорем, які означують тему. Для цього кожен вчитель сам визначає напрямок своєї роботи з учнями, підбирає типи і методи раціонального розподілу часу на вивчення кожної з підтем та розробляє, спираючись на досвід, свою методику. Це робота непроста і, аналізуючи власні спроби та помилки, пропоную для опрацювання вчителям-початківцям свою методику вивчення даної теми з підбором основних необхідних задач, лабораторної роботи та підсумкового уроку з даної теми. Ця методика опрацьована мною протягом 25 років викладання математики у старших класах, має позитивні результати, а  підсумковий урок з даної теми був представлений на районному семінарі вчителів математики.

Усі процеси, що відбуваються у природі чи людському суспільстві, є наслідком взаємодії багатьох факторів. Для того щоб вивчити ці процеси і надалі керувати ними, необхідно з’ясувати, яку роль у досліджуваному процесі відіграє кожний фактор окремо. Наприклад, у разі вивчення руху тіла слід з’ясувати, які сили спричинюють його рух, а які гальмують; яким чином саме рухоме тіло впливає на ті сили, що діють на нього. Досліджуючи процес зміни курсу деякої валюти, скажімо гривні, потрібно з’ясувати вплив багатьох економічних і соціальних факторів як внутрішніх, так і зовнішніх, що можуть істотно змінювати курс національної валюти щодо долара, німецької марки і т. ін.

Усі зазначені фактори необхідно подати з допомогою певних кількісних оцінок, а далі — скористатися відповідними математичними методами. Отже, щоб мати змогу застосувати математичні методи з метою вивчення взаємодії тих чи інших факторів, слід уміти виражати дію кожного з них кількісно.

Щоб дістати потрібні числові дані, необхідно провести серію спостережень. Отже, спостереження є найважливішою ланкою будь-якого експерименту. Слід, проте, ураховувати, що жодний найретельніше підготовлений експеримент не дозволяє виокремити саме той фактор, який для нас головний. Адже в здійснюваному експерименті ми не в змозі вилучити численні зайві фактори, які нас не цікавлять. Так, вивчаючи падіння тіла, ми не уникнемо дії на нього сил, зумовлених обертанням Земної кулі. Коли ж ідеться про хімічні реакції, нам ніколи не доведеться стикатися з чистими елементами. А досліджуючи вплив на врожайність тієї чи іншої культури внесеного в ґрунт добрива, ми не можемо знехтувати впливом інших факторів (опади, середня весняна температура, економічний стан регіону і т. ін.), які безпосередньо впливають на остаточний наслідок експерименту — урожайність.

Отже, кожне спостереження дає нам лише наслідок взаємодії основного фактора, який нас цікавить, з багатьма сторонніми, другорядними. Деякі з них потрібно й можна враховувати в дослідженнях. Урахування ж решти факторів або в принципі неможливе, або недоцільне з якихось міркувань. Тому за реальних умов під час дослідження будь-якого процесу застосовують метод його формалізації, беручи до уваги лише ті фактори, які істотно впливають на зазначений процес.

Водночас усі ті фактори, якими експериментатор нехтує, загалом від­биваються на наслідках експерименту, надаючи їм неоднозначності.

Так настають непередбачені наперед події, котрі називають випадковими. Випадкові події в масі спостережень підпорядковані, як з’ясували дослідники, певним характерним лише для них невипадковим законам.

Математична наука, що вивчає закономірності масових подій, називається теорією ймовірностей.

     Предмет теорії ймовірностей

 

Теорія ймовірностей вивчає закономірності, властиві випадковим явищам. Як будь-яка математична наука, вона має аксіоматичну побудову, з якої виводяться подальші результати. Основні поняття теорії ймовірностей мають не абстрактний характер. Вони в загальній формі відображають певні сторони реальної дійсності. Тому висновки і результати, що одержують у теорії ймовірностей, мають практичну цінність.

Випадковим називається таке явище, характер протікання якого не можна цілком передбачити на підставі наявних у нас даних. Неможливість передбачення не означає відсутності причинного зв'язку між початковими даними і результатом. Вона викликана неповною поінформованістю про цей зв'язок. Проте неповнота даних не є перешкодою для з'ясування загальних закономірностей, що властиві випадковим явищам. Експериментатору добре відома така універсальна схема: чим більша кількість дослідів, тим більш впевнено можна вивести закономірність, тим меншою є роль випадкових відхилень.

Теорія ймовірностей вивчає масові випадкові явища, тобто явища, що допускають хоча б експериментальну перевірку в однотипних умовах необмежену кількість разів. При цьому розглядаються такі випадкові явища, об'єктивні характеристики яких можуть бути отримані з будь-яким рівнем точності за будь-яких необмежених повторень експерименту.

Під випробовуванням у теорії ймовірностей розуміється експеримент, що може бути повтореним при дотриманні визначеного комплексу умов необмежену кількість разів. У зв’язку з тим, що завдання комплексу умов не вичерпує всіх обставин, які впливають на результат експерименту, при повторенні іспиту може спостерігатися різний результат експерименту.

Наприклад, експеримент полягає у тому, що з урни, в якій є m білих і М чорних куль, навмання виймають одну кулю. Комплекс умов: склад куль за кольором; витаскування кулі навмання.

Експеримент може бути повторено безліч разів, якщо вийнята куля повертається назад. Даний експеримент можна назвати випробуванням.

При зміні комплексу заданих умов, що характеризують випробування, буде одержано нове випробування.

Для кожного випробування можна вказати деяку систему можливих наслідків, головна властивість яких полягає в тому, що в результаті випробування відбувається один і тільки один з цих наслідків. Така система наслідків, пов'язаних з даним випробуванням, називається простором елементарних подій , а наслідки, що його складають, елементарними подіями . Їх взаємозв’язок можна наочно зобразити схемою, наведеною на рис.

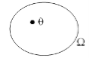
Рисунок 1

Класифікація подій. Події поділяються на вірогідні, неможливі та випадкові.

Якщо в результаті експерименту, здійснюваного з додержанням певного комплексу умов, певна подія обов’язково настає, то вона називається вірогідною. Вірогідна подія позначається символом  («омега»).

Наведемо приклади вірогідних подій.

Приклад 1

1. У земних умовах вода, нагріта до температури 100 С, набуває стану кипіння.

2. Якщо в урні міститься 10 однакових кульок, пронумерованих від 1 до 10, то кулька, навмання взята із цієї урни, має номер, що міститься в межах від 1 до 10.

Подія називається неможливою, якщо в результаті експерименту, проведеного з додержанням певного комплексу умов, вона не настає ніколи. Неможлива подія позначається символом  (порожня множина).

     Приклад 2

1. В урні міститься 10 однакових кульок, пронумерованих від 1 до 10. Навмання береться одна кулька. Поява кульки з номером 12 буде подією неможливою.

2. Якщо на дослідній ділянці посіяти 100 зернин ячменю, то подія, котра полягає в тому, що на момент збирання врожаю на цій ділянці з’явиться колосок пшениці, є неможливою.

Подія називається випадковою, якщо за певного комплексу умов у результаті експерименту вона може настати або не настати залежно від дії численних дрібних факторів, урахувати які дослідник не в змозі.

Випадкові події позначають символами А, В, С, … або А₁, А₂, А₃,…, А_k; В₁, В₂, …, В_n.

Отже, випадкові події пов’язані експериментами, наслідки яких є неоднозначними.

Приклад 3

1. Монету підкидають один раз. (Тут і далі припускаємо, що падає монета на рівну і тверду підлогу.) Поява герба (цифри) — подія випадкова.

2. Якщо на дослідній ділянці в лабораторних умовах посіяно 100 зернин ячменю, то не можна передбачити наперед, скіль­ки зернин проросте. Отже, подія, яка полягає в тому, що проросте від 1 до 100 зернин, є випадковою.

 

Теорія ймовірностей як один із розділів математики досліджує певний вид математичних моделей — моделі випадкових подій, а не самі такі події.

Математичні моделі, як відомо, відбивають найістотніші властивості досліджуваних об’єктів, абстрагуючись від неістотних.

Для математичного опису випадкових подій — наслідків експерименту — застосовують такі точні поняття: прості (елементарні) та складені випадкові події, простір елементарних подій.

Подія, що може відбутися внаслідок проведення однієї і лише однієї спроби (експерименту), називається простою (елементарною) випадковою подією.

Елементарні події позначаються _і (і = 1, 2, 3,…) і в теорії ймовір­ностей, так само як, скажімо, точка в геометрії, не поділяються на простіші складові.

Приклад 1. Монету підкидають один раз. Визначити елементарні події цього експерименту.

Розв’язання. Можливі такі елементарні випадкові події:

₁ = г (монета випаде гербом);

₂ = ц (монета випаде цифрою).

Приклад 2. Монету підкидають тричі. Визначити елементарні події цього експерименту.

Розв’язання. Триразове підкидання монети — це одна спроба. Елементарними випадковими подіями будуть:

₁ = ггг (тричі випаде герб);

₂ = ццц (тричі випаде цифра);

₃ = ггц

₄ = гцг  (герб випаде двічі);

₅ = цгг

₆ = гцц

₇ = цгц (герб випаде один раз).

₈ = ццг

Отже, цьому експерименту відповідають вісім елементарних подій.

Приклад 3. Задано дві множини цілих чисел ₁ = , ₂ = . Із кожної множини навмання беруть по одно­му числу. Визначити елементарні події цього експерименту — появу пари чисел.

₁ = 1; 1;  ₅ = 2; 1;  ₉   = 3; 1;

₂ = 1; 2;  ₆ = 2; 2;  ₁₀ = 3; 2;

₃ = 1; 3;  ₇ = 2; 3;  ₁₁ = 3; 3;

₄ = 1; 4;  ₈ = 2; 4;  ₁₂ = 3; 4.

Випадкова подія називається складеною, якщо її можна розкласти на прості (елементарні) події. Складені випадкові події позначаються латинськими великими літерами: A, B, C, D, … .

Приклад 4. Задано множину чисел  = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}. Навмання із цієї множини беруть одне число. Побудувати такі випадкові події: 1) з’явиться число, кратне 2; 2) число кратне 3; 3) число, кратне 5. Ці випадкові події будуть складеними. Позначимо їх відповідно А, В, С. Тоді А =
= {2, 4, 6, 8, 10, 12}; В = {3, 6, 9, 12}; С = {5, 10,}.

Елементарні випадкові події _і  A, _j  B, _k  C, які належать відповідно складеним випадковим подіям А, В, С, тобто є елементами цих множин, називають елементарними подіями, які сприяють появі кожної із зазначених подій унаслідок проведення експерименту (_і сприяють появі події А, _j — події В, _k — події С).

Кожному експерименту (спробі) з випадковими результатами (наслідками) відповідає певна множина  елементарних подій _i, кожна з яких може відбутися (настати) внаслідок його проведення: _і  . Множину називають простором елементарних подій.

Приклад 5. Гральний кубик, кожна грань якого позначена певною цифрою від 1 до 6, підкидають один раз. При цьому на грані випадає одна із зазначених цифр. Побудувати простір елементарних подій для цього експерименту (множину Ώ) і такі випадкові події: 1) А — випаде число, кратне 2;
2) В — випаде число, кратне 3.

Розв’язання. Оскільки кубик має шість граней, то в результаті експерименту може випасти одна із цифр від 1 до 6.

Отже, Ώ = 1, 2, 3, 4, 5, 6; 1) А = 2, 4, 6; 2) В = 3, 6.

Приклад 6. Монету підкидають чотири рази. Побудувати простір елементарних подій для цього експерименту і такі випадкові події:

1) А — герб випаде двічі; 2) В — герб випаде не менш як тричі.

Розв’язання. Шуканий простір елементарних подій:

Ώ = гггг, гггц, ггцг, гцгг, ццгг, ггцц, гццг, гцгц, цгцг, ццгг, цггц, гццц, цгцц, ццгц, цццг, цццц;

1) А = ггцц, ццгг, гцгц, цгцг, гццг, цггц;

2) В = гггг, гггц, ггцг, гцгг, цггг).

Простір елементарних подій може бути як дискретним, так і неперервним. Якщо множина є зчисленною (зліченною), тобто всі її елементи можна перелічити або принаймні пронумерувати (кожній елементарній події поставити у відповідність один і тільки один елемент нескінченної послідовності натуральних чисел 1, 2, 3, …), то простір елементарних подій називають дискретним. Він може бути обмеженим і необмеженим.

У противному разі (тобто коли кожній елементарній події не мож­на поставити у взаємно однозначну відповідність певне натуральне число) простір елементарних подій називають неперервним.

У розглянутих раніше прикладах простори елементарних подій були дискретними.

Приклади неперервних (недискретних) просторів елементарних подій дістанемо, розглянувши:

1) розміри однотипних деталей (діаметр, довжина), що їх виготов­ляє робітник або верстат-автомат;

2) покази приладів, що вимірюють масу, силу струму, напругу, опір і т. ін.

Отже, поняття елементарної події, простору елементарних подій є основними в теорії ймовірностей, як точка та пряма в аксіоматично побудованій евклідовій геометрії. Сама природа елементарних подій у теорії ймовірностей при цьому неістотна.

Простір елементарних подій є математичною моделлю певного ідеалізованого експерименту в тому розумінні, що будь-який можливий його наслідок описується однією і лише однією елементарною подією — наслідком експерименту.

Мовою теорії множин випадкова подія А означується як довільна непорожня підмножина множини  (А  ).

      

     Операції над подіями

 

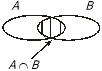
Додавання. Сумою двох подій А і В називається така подія С = АВ (С = А + В), яка внаслідок експерименту настає з настанням принаймні однієї з подій А або В. Подію АВ схематично зображено на рис. 1 заштрихованою областю.

Рис. 1

Операція АВ називається об’єднанням цих подій.

Множення. Добутком двох подій А і В називається така подія С = АВ (С = АВ), яка внаслідок експерименту настає з одночасним настанням подій А і В.

Операція АВ називається перерізом цих подій (рис. 2).

Рис. 2

Віднімання. Різницею двох подій А і В називається така подія
С = А \ В (С = А – В), яка внаслідок експерименту настає з настанням події А і одночасним ненастанням події В (рис. 3).

Рис. 3

Приклад. Задано множину цілих чисел Ώ = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15. Навмання з неї беруть одне число.

Побудувати випадкові події: 1) А — узяте число кратне 2;
2) В — кратне 3.

Визначити АВ; А∩В; А \ В.

Розв’язання. 1) А = 2, 4, 6, 8, 10, 12, 14; 2) В = 3, 6, 9, 12, 15.

Звідси дістаємо:

АВ = 2, 4, 6, 8, 10, 12, 14 3, 6, 9, 12, 15 = 2, 3, 4, 6, 8, 9, 10, 12, 14, 15;

А∩В = 2, 4, 6, 8, 10, 12, 14 ∩ 3, 6, 9, 12, 15 = 6, 12;

А \ В = 2, 4, 6, 8, 10, 12, 14 \ 3, 6, 9, 12, 15 = 2, 4, 8, 10, 14.

Якщо А∩В  , то випадкові події А і В називають сумісними.

Якщо А∩В = , то такі випадкові події А і В називають несумісними.

Повна група подій. Протилежні події. Якщо А₁A₂A₃…
…A_n = = , то такі випадкові події утворюють повну групу, а саме: внаслідок експерименту якась із подій А_і обов’язково настане.

Приклад. При одноразовому підкиданні грального кубика обов’язково з’явиться одна із цифр, що є на його гранях, а саме: А₁ = 1, А₂ = 2, А₃ = 3, А₄ = 4, А₅ = 5, А₆ = 6. Отже, випадкові події А_і (і = ) утворюють повну групу: = Ω =
= 1, 2, 3, 4, 5, 6.

Дві несумісні випадкові події, що утворюють повну групу, називають протилежними.

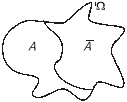
Подія, яка протилежна А, позначається . Протилежні події у просторі елементарних подій ілюструє рис. 4. Він унаочнює також співвідношення: А = Ω,  А∩ = .

Рис. 4

Випадкові події А, В, С (А  Ω, В Ω, С Ω), для яких визначено операції додавання, множення та віднімання, підлягають таким законам:

1. АА = А, АА = А.
2. АВ = ВА. 3. АВ = ВА.	Комутативний закон для операцій додавання та множення.
4. (АВ) С = А (ВС). 5. (АВ) С = А (ВС).		Асоціативний закон для операцій додавання та множення.
6. (АВ) С = (АС) (ВС).				Перший дистрибутивний закон.
7. (АВ) С = (АС) (ВС).					Другий дистрибутивний закон.

8. АΩ = Ω.

9. АΩ = А.

10. А = А.

11. А = .

12. = Ω \ А.

13. = .

14. = Ω.

15. А(А) = А; В = В (В).

16. .

17. .

Елементарні випадкові події задовольняють такі твердження: 1) між собою несумісні; 2) утворюють повну групу; 3) є рівноможливими, а саме: усі елементарні події мають однакові можливості відбутися внаслідок проведення одного експерименту.

Для дискретного простору Ω перші два твердження можна записати так: 1) ω_іω_j = , і ј; 2) = Ω.

Для кількісного вимірювання появи випадкових подій і їх комбінацій уводиться поняття ймовірності події, що є числом такої ж природи, як і відстань у геометрії або маса в теоретичній механіці.

 

Класичне означення ймовірності

 

Імовірністю випадкової події А називається невід’ємне число Р(А), що дорівнює відношенню числа елементарних подій m (0 m n), які сприяють появі А, до кількості всіх елементарних подій n простору Ω:

 Р (А) = .  (1)

Для неможливої події Р () = 0  (m = 0);

Для вірогідної події Р (Ω) = 1 (m = n).

Отже, для довільної випадкової події

 . (2)

Приклад 1. У ящику міститься 15 однотипних деталей, із яких 6 бракованих, а решта — стандартні. Навмання з ящика береться одна деталь. Яка ймовірність того, що вона буде стандартною?

Розв’язання. Число всіх рівноможливих елементарних подій для цього експерименту:

n = 15.

Нехай А — подія, що полягає в появі стандартної деталі. Число елементарних подій, що сприяють появі випадкової події А, дорівнює дев’яти
(m = 9). Згідно з (1) маємо:

.

Приклад 2. Гральний кубик підкидають один раз. Яка ймовірність того, що на грані кубика з’явиться число, кратне 3?

Розв’язання. Число всіх елементарних подій для цього експерименту n = 6. Нехай В — поява на грані числа, кратного 3. Число елементарних подій, що сприяють появі В, дорівнює двом (m = 2).

Отже,

.

Приклад 3. Два гральні кубики підкидають по одному разу. Побудувати простір елементарних подій — множину Ώ і такі випадкові події:

А — сума цифр виявиться кратною 4;

В — сума цифр виявиться кратною 3.

Обчислити Р (А), Р (В), Р (АВ).

Розв’язання. Простір елементарних подій — множину  запишемо у вигляді таблиці:

Кубик 2-й	Кубик 1-й
	1	2	3	4	5	6
1	1,1	1,2	1,3	1,4	1,5	1,6
2	2,1	2,2	2,3	2,4	2,5	2,6
3	3,1	3,2	3,3	3,4	3,5	3,6
4	4,1	4,2	4,3	4,4	4,5	4,6
5	5,1	5,2	5,3	5,4	5,5	5,6
6	6,1	6,2	6,3	6,4	6,5	6,6

Отже, простір елементарних подій  містить n = 36 пар чисел.

Події А і В визначимо з допомогою побудованої таблиці так: елементарні події, які сприяють появі А (сума цифр кратна 4), заштриховані вертикальними лініями, а для В (сума кратна 3) — горизонтальними лініями. Звідси маємо: число елементарних подій, що сприяють появі А, дорівнює дев’яти (m₁ = 9), а число елементарних подій, що сприяють появі В, — дванадцяти (m₂ = 12), число елементарних подій, що сприяють появі події АВ, дорівнює одиниці (m₃ = 1) (темні клітинки таблиці).

Остаточно дістаємо:

.

Приклад 4. У кожній із трьох урн містяться червоні та сині кульки. Із кожної урни навмання беруть по одній кульці. Побудувати простір елементарних подій для цього експерименту — множину  і такі випадкові події:

А — серед трьох навмання взятих кульок дві виявляються червоного кольору;

В — серед трьох кульок дві виявляються синього кольору. Обчислити Р (А), Р (В), Р (АВ).

Розв’язання. Позначимо появу кульки червоного кольору як Ч, а синього кольору як С. Тоді простір елементарних подій буде такий: = ЧЧЧ, ЧЧС, ЧСЧ, СЧЧ, ЧСС, СЧС, ССЧ, ССС, n = 8.

Події: А = ЧЧС, ЧСЧ, СЧЧ, m₁ = 3;

В = ССЧ, СЧС, ЧСС, m₂ = 3.

Події А і В є несумісними (АВ = ).

Обчислюємо: ; ; Р (АВ) = 0.

Приклад 5. В електричну мережу увімкнено чотири електролампочки. При проходженні електричного струму в мережі кожна електролампочка із певною ймовірністю може перегоріти або не перегоріти. Побудувати простір елементарних подій (множину ) — числа електролампочок, які не перегорять, і такі випадкові події:

А — із чотирьох електролампочок перегорять не більш як дві;

В — не менш як три. Обчислити Р (А), Р (В), Р (АВ).

Розв’язання. Нехай А_i (і = ) відповідно першу, другу, третю та четверту електролампочку, що не перегорять, а — що перегорять. Тоді простір елементарних подій буде:

 = А₁ А₂ А₃ А₄,  А₁ А₂ А₃  А₁ А₂А₄,  А₁А₃ А₄, А₂ А₃ А₄, А₁ А₂, А₃ А₄, А₂А₄, А₁А₃, А₁А₄, А₂ А₃, А₁, А₂, А₃, А₄, ,   n = 16.

Випадкові події:

А = А₁ А₂, А₃ А₄, А₁А₃, А₂А₄, А₁А₄, А₂ А₃, А₂ А₃ А₄,  А₁А₃ А₄,  А₁ А₂А₄,  А₁ А₂ А₃,  А₁ А₂ А₃ А₄, m₁ = 11.

В = А₁ А₂, А₃ А₄, А₁А₃, А₂А₄, А₁А₄, А₂ А₃, А₁, А₂, А₃, А₄, , m₂ = 11.

АВ = А₁ А₂, А₃ А₄, А₁А₃, А₂А₄, А₁А₄, А₂ А₃, m₃ = 6.

;  ;  .

 

Елементи комбінаторики в теорії ймовірностей: перестановки,
розміщення та комбінації

 

При розв’язуванні задач з теорії ймовірностей побудувати простір елементарних подій (множину ) можна не завжди.

Для більшості прикладних задач така побудова пов’язана з виконанням великого обсягу робіт, а нерідко й взагалі неможлива. Щоб обчислити ймовірність тієї чи іншої випадкової події для певного класу задач із дискретним і обмеженим простором елементарних подій, необхідно вміти обчислити кількість n усіх елементарних подій (елементів множини ) і число m елементарних подій, які сприяють появі випадкової події.

Існує клас задач, в яких для обчислення n і m використовуються елементи комбінаторики: переставлення, розміщення та комбінації. У комбінаториці оперують множинами однотипних елементів.

Загалом множини бувають упорядковані та невпорядковані.

Множину називають упорядкованою, якщо при її побудові істотним є порядок розміщення елементів.

У противному разі множину називають невпорядкованою.

Перестановки. Перестановками із n елементів називають такі впорядковані множини з n елементів, які різняться між собою порядком їх розміщення.

Кількість таких упорядкованих множин обчислюється за формулою

 ,  (3)

де n набуває лише цілих невід’ємних значень.

Оскільки , то при n = 1 маємо

1! = 0!

Отже,        0! = 1.

Приклад 1. На кожній із шести однакових карток записано одну з літер

Я, І, Р, Е, О, Т.

Яка ймовірність того, що картки, навмання розкладені в рядок, утворять слово

Т

Е

О

Р

І

Я

?

Розв’язання. Кількість усіх елементарних подій (елементів множини Ω)

n = 6! = 6  5  4  3  2  1 = 720.

Кількість елементарних подій, що сприяють появі слова ТЕОРІЯ,
m = 1. Позначивши розглядувану подію через В, дістанемо:

.

Приклад 2. Задано множину цілих чисел Ω = 1, 2, 3, 4, 5. Її елементи навмання розставляють у рядок. Обчислити ймовірності таких випадкових подій:

А — розставлені в ряд числа утворюють зростаючу послідовність;

В — спадну послідовність;

С — цифра 1 стоятиме на першому місці, а 5 — на останньому;

D — цифри утворять парне п’ятицифрове число.

Розв’язання. Простір елементарних подій для цього експерименту міститиме n = 5! = 1  2  3  4  5 = 120 несумісних, рівноймовірних елементарних подій.

Кількість елементарних подій, що сприяють появі А, дорівнює одиниці (m₁ = 1).

Кількість елементарних подій, що сприяють появі В, дорівнює одиниці (m₂ = 1).

Для випадкової події С   m₃ = 3!

Для випадкової події D   m₄ = 4! 2 = 48.

Обчислюємо: ;  ;

;      .

Розміщення. Розміщенням із n елементів по m (0) називаються такі впорядковані множини, кожна із яких містить m елементів і які відрізняються між собою порядком розташування цих елементів або хоча б одним елементом.

Кількість таких множин обчислюється за формулою

 . (4)

Наприклад, .

Приклад 1. Маємо дев’ять однакових за розміром карток, на кожній з яких записано одну з цифр: 1, 2, 3, 4, 5, 6, 7, 8, 9. Навмання беруть чотири картки і розкладають в один рядок. Яка ймовірність того, що при цьому дістанемо

1

9

7

3

?

Розв’язання. Кількість елементарних подій множини  буде .

Кількість елементарних подій, що сприяють появі 1, 9, 7, 3, дорівнює одиниці (m = 1). Позначимо цю випадкову подію через В. Тоді

.

Приклад 2. У кімнаті перебувають 10 студентів. Яка ймовірність того, що два і більше студентів не мають спільного дня народження?

Розв’язання. Вважаємо, що рік має 365 днів. Для кожного студента в загальному випадку існує 365, а для 10 студентів — 365¹⁰ можливих днів народження. Отже, маємо n = 365¹⁰ елементарних подій множини Ω. Позначимо через В випадкову подію, яка полягає в тому, що дні народження студентів не збігаються. Кількість елементарних подій, що сприяють появі В, .

Остаточно маємо: .

Комбінації. Комбінаціями з n елементів по називаються такі множини з m елементів, які різняться між собою хоча б одним елементом.

Кількість таких множин

 .  (5)

Приклад 1. У цеху працює 10 верстатів-автоматів, кожний із яких може з певною ймовірністю перебувати в роботоздат­ному стані або в стані поломки. Яка ймовірність того, що під час роботи верстатів-автоматів із ладу вийдуть три з них?

Розв’язання. Оскільки кожний верстат-автомат може перебувати у двох несумісних станах — роботоздатному або нероботоздатному, то кількість усіх елементарних подій множини Ω буде n = 2¹⁰.

Позначимо через А випадкову подію — із ладу вийде три верстати з десяти. Тоді кількість елементарних подій, що сприяють появі А, буде

.

Отже,

.

Приклад 2. У шухляді міститься 10 одинотипних деталей, 6 із яких є стандартними, а решта бракованими. Навмання із шухляди беруть чотири деталі. Обчислити ймовірність таких випадкових подій:

А — усі чотири деталі виявляються стандартними;

В — усі чотири деталі виявляються бракованими;

D — із чотирьох деталей виявляються дві стандартними і дві бракованими.

Розв’язання. Кількість усіх елементарних подій множини Ω

;

кількість елементарних подій, що сприяють події А:

;

кількість елементарних подій, що сприяють появі В:

;

кількість елементарних подій, що сприяють появі D:

.

Обчислимо ймовірності цих подій:

;

;

.

 

Аксіоми теорії ймовірностей та їх наслідки

 

Загалом функції дійсних змінних бувають визначеними не на всій множині дійсних чисел, а лише на певній її підмножині, яку називають областю визначення функції.

Імовірність також не завжди можна визначити для будь-яких підмножин множини Ω (простору елементарних подій). Тому доводиться обмежуватися певним класом підмножин, до якого висуваються вимоги замкненості відносно операцій додавання, множення та віднімання.

Нехай задано довільний простір елементарних подій — множину Ω і  — деяка система випадкових подій.

Система подій називається алгеброю подій, якщо:

1. Ώ  .

2. Із того, що А  , В  , випливає: що АВ   , АВ  , А \ В  .

Із тверджень 1 і 2 дістаємо, що Ø = Ώ \ Ώ, а отже, Ø  . Наймен­шою системою, яка буде алгеброю подій, є  = (Ø, Ώ). Якщо Ώ — обмежена множина, то система  також буде обмеженою. Якщо множина містить n елементів, то кількість усіх підмножин буде 2ⁿ.

Якщо Ω є неперервною множиною, то система  утворюється квадровними підмножинами множини Ω, які також утворюють алгебру подій.

Числова функція Р, що визначена на системі подій , називається ймовірностю, якщо:

1.  є алгеброю подій.

2. Для будь-якого А   існує .

3. Р (Ω) = 1.

4. Якщо А і В є несумісними (АВ = Ø), то

 .  (6)

Для розв’язування задач з нескінченними послідовностями подій, наведені аксіоми необхідно доповнити аксіомою неперервності.

5. Для будь-якої спадної послідовності подій із , такої, що Ø, випливає рівність

.

Трійка (, Ω, Р), де  є алгеброю подій і Р задовольняє аксіоми 1—5, називається простором імовірностей.

Приклад 1. Задано множину цілих чисел Ω = 1, 2, …, 30. Навмання з цієї множини беруть одне число. Яка ймовірність того, що воно виявиться кратним 5 або 7?

Розв’язання. Простір Ω містить n = 30 елементарних подій.

Позначимо через А подію, що полягає в появі числа, кратного 5, а через В у появі числа, кратного 7. Тоді дістанемо:

;

;

Ø.

Згідно з (6) маємо:

.

Приклад 2. Садівник восени посадив 10 саджанців яблуні. Кожний із саджанців може прийнятись або не прийнятись із певною ймовірністю. Яка ймовірність того, що з 10 саджанців навесні наступного року приймуться 6 або 2?

Розв’язання. Множина Ω містить n = 2¹⁰ елементарних подій. Нехай А — випадкова подія, яка полягає в тому, що число саджанців, котрі проросли, дорівнює 6; В — число саджанців, що проросли, дорівнює 2.

Кількість елементарних подій, які сприяють появі А:

.

Кількість елементарних подій, що сприяють появі В:

.

Оскільки АВ = Ø, маємо:

.

Приклад 3. У ящику міститься 13 однакових деталей, серед яких 5 є бракованими, а решта — стандартними. Навмання з ящика беруть чотири деталі. Яка ймовірність того, що всі чотири деталі виявляться стандартними або бракованими?

Розв’язання. Множина Ω містить
елементарних подій. Позначимо через А появу чотирьох стандартних деталей. Кількість елементарних подій, що сприяють появі А: . Позначимо через В появу чотирьох бракованих деталей. Кількість елементарних подій, що сприяють появі В, .

Згідно з (6) дістанемо:

.

Наслідки аксіом

1. Якщо випадкові події А₁, А₂, А₃, … А_n є несумісними попарно, то

 . (7)

2. Якщо випадкові події А_1, А₂, А₃, … А_n  утворюють повну групу, то

 . (8)

Із рівності А = Ω і аксіом 3, 4 випливає, що

 . (9)

Якщо Ø, то

 . (10)

Справді:

, то

 Ø).  (11)

Оскільки

і при цьому = Ø, то

Отже,

.

3. Формула додавання для n сумісних випадкових подій має такий вигляд:

  (12)

Наприклад, для трьох сумісних випадкових подій формулу (12) можна записати так:

 .  (13)

4. Якщо випадкова подія А сприяє появі , то

 . (14)

Приклад 1. В урні містяться 30 однакових кульок, які пронумеровані від 1 до 30. Навмання із урни беруть одну кульку. Яка ймовірність того, що номер кульки виявиться кратним 3 або 5?

Розв’язання. Кількість усіх елементарних подій множини Ω n = 30.

Позначимо через А = 3, 6, 9, 12, 15, 18, 21, 24, 27, 30 (m₁ = 10) —
появу кульки з номером, кратним 3, а через В = 5, 10, 15, 20, 25, 30
(m₂ = 6) — появу кульки із номером, кратним 5.

є подіями сумісними.

Згідно з (10) дістанемо

.

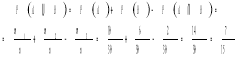Приклад 2. Чотири спортсмени мають виконати норму майстра спорту. Кожний із них може виконати її із певною ймовірністю. Яка ймовірність того, що із чотирьох спортсменів норму майстра спорту виконують не менш як два спортсмени; не більш як три?

Розв’язання. Позначим через А₁ А₂ А₃ А₄ випадкові події, що відповідно перший, другий, третій та четвертий спортсмени виконають норму майстра, а через — відповідно випадкові події, що перший, другий, третій та четвертий спортсмени не виконають норму. Тоді простір елементарних подій для цього експерименту буде:

 = А₁ А₂ А₃ А₄, А₁ А₂ А₃, А₁ А₂А₄, А₁А₃ А₄, А₂ А₃ А₄, А₁ А₂, А₃ А₄, А₂А₄, А₁А₃, А₁А₄, А₂ А₃, А₁, А₂, А₃, А₄, , n = 16.

Випадкові події:

А = А₁ А₂,  А₃ А₄,  А₁А₃,  А₂А₄,  А₁А₄, А₂ А₃, А₂ А₃ А₄, А₁А₃ А₄, А₁ А₂А₄, А₁ А₂ А₃, А₁ А₂ А₃ А₄,  m₁ = 11;

В = А₁ А₂ А₃, А₁ А₂А₄, А₁А₃ А₄, А₂ А₃ А₄, А₁ А₂, А₃ А₄, А₂А₄, А₁А₃, А₁А₄, А₂ А₃, А₁, А₂, А₃, А₄, ,  m₂ = 15;

АВ = А₁ А₂ А₃, А₁ А₂А₄, А₁А₃ А₄, А₂ А₃ А₄, А₁ А₂, А₃ А₄, А₂А₄, А₁А₃, А₁А₄, А₂ А₃,  m₃ = 10.

Шукана ймовірність:

.

Приклад 3. Випадкові події А₁, А₂, А₃, А₄ є попарно несумісними і утворюють повну групу. Знайти Р (А₁), Р (А₂), Р (А₃), Р (А₄), коли відомо, що Р (А₁) = 0,2 Р (А₂), Р (А₂) = 0,8
Р (А₃), Р (А₃) = 0,5 Р (А₄).

Розв’язання. Оскільки випадкові події А₁, А₂, А₃, А₄ є попарно несумісними і утворюють повну групу, то згідно з (8) дістаємо:

.

За умовою задачі знаходимо:

Р (А₂) = 0,8 Р (А₃) = 0,8  0,5 Р (А₄) = 0,4 Р (А₄).

Р (А₁) = 0,2 Р (А₂) = 0,2  0,4 (А₄) = 0,08 Р (А₄).

Отже,

0,08 Р (А₄) + 0,4 Р (А₄) + 0,5 Р (А₄) + Р (А₄) = 1;

;

;

;

.

 

Геометрична ймовірність

 

Класичне означення ймовірності придатне лише для експериментів з обмеженим числом рівномірних елементарних подій, тобто коли множина Ώ (простір елементарних подій) обмежена.

Якщо множина Ώ є неперервною і квадровною, то для обчислення ймовірності А (А  Ώ) використовується геометрична ймовірність

 . (15)

Якщо множина Ώ вимірюється в лінійних одиницях, то Р (А) дорівнюватиме відношенню довжини, якщо Ώ вимірюється у квадратних одиницях, то Р (А) дорівнюватиме відношенню площ, і т. ін.

Приклад 1. По трубопроводу між пунктами А і В перекачують нафту. Яка ймовірність того, що пошкодження через певний час роботи трубопроводу станеться на ділянці довжиною 100 м.

Розв’язання. Простір елементарних подій Ώ = , тоді (А  Ώ).

Згідно з (12) маємо:

.

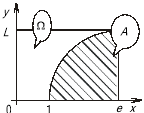
Приклад 2. Задана множина Ώ = (0  х  е, 0  у  1). Яка ймовір­ність того, що навмання взяті два числа (х, у) утворять координати точки, яка влучить в область А = (1 х  е,
0  у  ln х)?

Розв’язання. Множини Ώ і А зображені на рис. 5.

Рис. 5

.

 

Статистична ймовірність

 

На практиці обчислити ймовірності випадкових подій можна лише для обмеженого класу задач як для дискретних, так і для неперервних просторів елементарних подій (множини Ώ). Для більшості задач, особливо економічних, обчислити ймовірності практично неможливо. У цьому разі використовується статистична ймовірність.

Насамперед уводиться поняття відносної частоти випадкової події W (A).

Відносною частотою випадкової події А W(A) називається відношення кількості експериментів m, при яких подія А спостерігалася, до загальної кількості n проведених експериментів:

 .   (16)

Як і для ймовірності випадкової події, для відносної частоти виконується нерівність

.

Теорія ймовірностей вивчає лише такі випадкові події, в яких спостерігається стабільність відносних частот, а саме: у разі проведення k серій експериментів існує така константа Р(А), навколо якої групуватимуться відносні частоти досліджуваної випадкової події А, тобто W_і (А). І це групування буде тим ближчим до цієї константи, чим більшим буде число n експериментів.

На рис. 6 показано, як W_і (А) змінюється зі збільшенням n експериментів.

Рис. 6

Імовірність випадкової події визначається так: упевнившись, що існує стабільність відносних частот випадкової події W_і (А), задаємось малим додатним числом  і проводимо серії експериментів, збільшуючи їх число n. Якщо на якомусь кроці серії експериментів виконуватиметься нерівність , то за ймовірність випадкової події береться одне з чисел W_і або W_{і – 1}. Ця ймовірність називається статистичною.

     Розібрані вправи

З безлічі подружніх пар навмання вибирається одна пара. Подія А: "чоловіку більше 30 років", подія В: "чоловік старше дружини", подія С: "дружині більше 30 років".

а) З'ясувати, в чому полягають події АВС, А-АВ, .

б) Перевірити, що .

Відповідь: а) АВС - "обидва: і чоловік, і дружина - старше 30 років, причому чоловік старше дружини"; А-АВ - "чоловіку більше 30 років, але він не старше своєї дружини"; - "обидва: і чоловік, і дружина - старше 30 років, причому чоловік не старше своєї дружини";

б) - "чоловіку більше 30 років" і "дружині не більше 30 років", отже чоловік старше дружини - В, тобто.

2. Нехай А, В, С - три довільних події. Визначити подію, що полягає в тому, що з А, В, С

а) відбулося тільки А;

б) відбулися тільки А та В;

в) усі три події відбулися;

г) відбулася принаймні одна з подій;

д) відбулися принаймні дві події;

е) відбулася одна і тільки одна подія;

ж) відбулися дві і тільки дві події;

з) жодна подія не відбулася;

і) відбулося не більше двох подій.

Відповідь:

ж)

 

3. Нехай А та В - довільні події, U - достовірна подія, а V - неможлива подія. Довести, що А, , , U, V утворять повну групу подій.

Відповідь: Легко перевірити, що перші три події попарно несумісні, сума їх дорівнює U.

4. У чому полягає умова сумісності подій А+В, і ?

Відповідь: З того, що (А+В) (, випливає необхідність сумісності А і В.

5. Довести, що подія (А+В) ( є неможливою.

6. Чи є рівносильними події А і В, якщо

а)

б) А+С=В+С?

в) АС=ВС?

 

Відповідь: а) так; б) взагалі кажучи, необов’язково в) взагалі кажучи, необов’язково.

7. Нехай А, В, С - довільні події. Спростити дані вирази для подій:

а) (А+В) (В+С);

б) (А+В) (А+).

 

Відповідь:

а) (А+В) (В+С) =АВ+АС+ВВ+ВС= (А+В+С) В+АС=В+АС;

б) (А+В) (А+) = АА+АВ+А+В=А+А (В+) += А+А+=А.

 

Лабораторна робота на тему:

«Теорія імовірностей, елементи комбінаторики»

 

1) В регіонах (4) А - країн з розвинутою економікою та В - країн з перехідною економікою, Україна входить до дванадцятки з перехідною економікою. Якщо брати з регіону одну на вибір країну, то визначити:

•                 Ймовірність появи розвиненої країни
•                 Появу країни з перехідною екномікою

Де А = 4, В = 12.

Р(А)= А/А+В = 1/4

Р(В)= В/А+В = 12/16 = ¾

 2) В регіонах а- країн з розвинутою економікою та b- країн з перехідною економікою (А,В≥2). де a, b з умови першої задачі. Якщо брати 2 країни з регіону на вибір, то визначити:

1.                  Ймовірність появи країн розвинених
2.                   Ймовірність появи країн з перехідною економікою
3.                   Ймовірність появи країн різних

Виначимо загальне число можливих варіацій:

поява країн розвинених ;

ймовірність появи країн розвинених  Р(А)=

поява країн з перехідн. екон.

ймовірність появи країн з перехідн. екон: Р(В)=

поява країн розвинених ;

ймовірність появи країн розвинених  Р(С)=

3) Є два регіони. У першому а-країни мирні, b-країни агресивні, у другому с-країни мирні d-агресивні.

 а=4

 b=12

 с=3

 d=5

Визначити ймовірнісь того, що при обранні з кожного регіону по 2 країни буде взято:

1.                  -Обидві мирні
2.                   -Обидві агресори
3.                   –різні

Визначимо загальну кількість можливих комбінацій обрання країн:

               

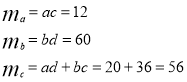
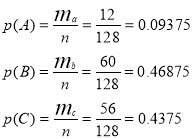
4) Розклад на 1 день містить 5 пар. Визначити кількість таких можливих розкладів з 11 дисципдін, при умові, що жодна не повторюєьтся.

Даний вираз є сполученням з 11 елементів по 5, оскільки з 11 елементів обирають 5 будь-яких незалежно від їх розміщення, але без повторення.

Можливими є 47520 розкладів, що задовольняють умову задачі.

 5) На вхід до інф.-аналіт. відділу поступає з ймовірністю Р1 суміш корисної інформації з завадою, а завада поступає лише з ймовірністю (1-Р1). Відділ реєструє корисну інформацію з ймовірністю З2, а тільки заваду – з ймовірністю Р3. Відділ зареєстрував наявність корисної інформації. Знайти ймовірність того, що в суміші була корисна інформація.

 Складемо гіпотези:

Н₁ – в суміші є корисна інформація;

Н₂ – в суміші немає корисну інформації;

Р(Н₁) = р₁   Р(Н₂) = 1-р₁

Рн₁(А) = р₂   Рн₂(А) = р₃

 

 

Р(А) = (Р(Н₁)*Рн₁(А))+(Р(Н₂)*Рн₂(А))=р₁*р₂+(1-р₁)р₃

Повн. Ймовірн.       ум. ймовірн. корисн.    Ум. ймовірн. завади

;

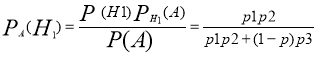 де: р1=1/4;

       р2=1/12;

       р3=1/3;

підставивши дані у формулу отримаємо:

 

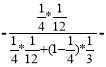
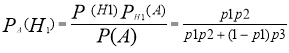=                         0.076923076923 

 

Ймовірність того, що відділ отримав корисну інформацію з суміші рівна приблизно 0.08

 6) На потоці вчаться 50 студентів. 10 – відмінники (а), 25 – хорошисти (в), 15 – трієчники (с). На екзаменаційні білети відмінник знає відповіді на всі 100, хорошист на 80, а трієчник – на 60. Викликали студента і він відповів лише на 4 питання з 5 поставлених. Знайти ймовірність того, що це був відмінник, хорошист, трієчник.

n– загальна кількість = 50, a = 10, b = 25, c = 15.

Р(Н₁)=с/n= 15/50 – викликали трієчника 

Р(Н₂)=b/n= 25/50 – викликали хорошиста

Р(Н₂)=a/n= 10/50 – викликали відмінника

 Розрахуємо ймовірність відповідей трієчника:

L1= 60 – зможе відповісти

L2= 40 – не зможе

Р(L₁)=60/100 Р(4з5/Н₁)=(60/100)⁴*40/100=324/6250

Р(L₂)=40/100

Розрахуємо ймовірність відповідей хорошиста:

L₁= 80 – зможе відповісти

L₂= 20 – не зможе

Р(L₁)=80/100 Р(4з5/Н₂)=(80/100)⁴*20/100=256/2125

Р(L₂)=20/100

Розрахуємо ймовірність відповідей відмінника:

L₁= 100 – зможе відповісти

L₂= 0 – не зможе

Р(L₁)=1 Р(4з5/Н₃)= 1⁴ *0=0

Р(L₂)=20/100

 Для обчислення задачі використаємо формулу повної ймовірності:

Р(4з5)=Р(Н₁)*Р(4з5/Н₁)+ Р(Н₂)*Р(4з5/Н₂)+Р(Н₃)*Р(4з5/Н₃)=0.06

Оскільки це не міг бути відмінник, то розрахуємо ймовірність для трієчника й хорошиста:

Р(Н₁/4з5)=р(Н₁)*Р(435/Н₁)/Р(4з5)=70%

Р(Н₁/4з5)=р(Н₂)*Р(435/Н₂)/Р(4з5)=30%

 Ймовірність того, що це був хорошист = 70 %, а трієчник = 30% відповідно.

УЗАГАЛЬНЮЮЧИЙ УРОК

Слайд 1

Добрий день, шановні колеги! Ми раді вітати вас у нашому НВК і раді представити вам узагальнюючий урок з однієї з найскладніших для нашого розуміння тем, які вивчаються у курсі математики 11 класу, - «Теорії імовірностей».

Мета нашого уроку: Зробити екскурс у історію виникнення стохастичної науки «Теорія імовірності» та історію введення її основ у шкільний курс математики; узагальнити основні поняття цієї науки; поставити проблему вибору і показати способи її розв`язання; показати зв`язок математичної теорії імовірності з економікою, генетикою, теорією ігор та іншими науками. Та що там багато розмовляти. Розпочинаємо урок.

Слайд 2

Від шахової гри – аристократки марної – теорії достойної не народилось жодної,

а гра у кості, хоч і примітивна,

науку про ймовірність народила дивну. Воістину в науці, як в житті:

Найглибша мудрість – в просторі!

                                                                                           Г.П Бевз

 

Коли ми починаємо говорити про якесь поняття, ми намагаємось собі його якось означити або уявити. Говорячи про імовірність, ми, більшою мірою уявляємо її собі в яскравих картинках. Так уявили теорію імовірності учні цього класу. (стенд з роботами учнів)

Та все ж… як виникла ця наука і кому ми зобов`язані її вивченням у школі?

Слайди 3-22

Гриценко Н. Історія виникнення теорії імовірностей

Це мабуть важко зробити, але все ж спробуємо. Заглянемо в часи Стародавнього Єгипту. Звідти до нас дійшли певні закономірності випадкових подій, правда тоді вважалося, що вони залежать від волі Богів.

Відомо, що в 2238 р. до нашої ери в Китаї за часів імператора Яо було проведено перепис населення і помічено, що незалежно від того, що кількість дівчаток і хлопчиків в окремій сім`ї може різнитися, взагалі в общині це співвідношення майже вирівнюється.

Взагалі уявлення про стохастику – науку про експерименти над випадковими подіями, та про підрахунок сприятливих комбінацій при грі в кості можна зустріти ще в «Божественной комедии» Данте. Однак більш-менш строгий аналіз випадкових явищ можна зустріти у працях Луки Пачолі (1445-1514 рр). Саме він розпочав І період даної науки. До активного накопичення матеріалу беруться Джероламо Кардано (1501-1576), Ніколо Тарталья (1500-1557), Галілео Галілей (1564-1642). Його афоризм «вимірюй усе, що вимірюється й зроби невимірне вимірним» є актуальним і в наш час.

А от теорія імовірності як математична наука зародилася в середині XVII століття. Її означили видатні математики: Блез Паскаль (1623-1662), П`єр Ферма (1601-1665), Христіан Гюйгенс (1629-1695), який видав перший трактат з теорії імовірності «Про розрахунки в азартних іграх».

Через 10 років після смерті відомого філософа Бенедикта Спінози (1632-1677) було опубліковано його працю «Замітки про математичну ймовірність», де вперше говориться саме про таку ймовірність, хоч саме поняття і не визначається.

ІІІ період розвитку теорії імовірності характеризується дійсно науковими досягненнями: теоремами, способами, формулами, задачами. Найвидатнішими відкриттями стали праці П`єра Сімона Лапласа (1749-1827), Сімеона Пуассона (1781-1840). Першими дослідниками теорії стали швейцарські вчені Якоб Бернуллі (1654-1705), Ніколай Бернуллі (1687-1759), Даніїл Бернуллі (1700-1782) та російські: Леонард Єйлер (1707-1783), Михайло Васильович Остроградський (1801-1862), Віктор Якович Буняковський (1804-1889), Панфутій Львович Чебишев (1812-1894).

IV період розвитку теорії імовірностей ознаменувався тріумфом Петербурзької математичної школи, провідна роль в якій належить П.Л.Чебишеву (1821-1894) та його учням. Вирішальний етап розвитку теорії імовірностей ознаменувала праця «Основні поняття теорії імовірностей» Андрія Миколайовича Колмогорова (1903-1987) та теоретико-імовірнісні передумови броунівського руху Альберта Енштейна (1879-1955).

У 1938 році, коли Олександр Якович Хінчин (1894-1959) став керівником фізико-математичної секції навчально-методичної ради і кабінету математики у Вільнюсі, він зосередив свою увагу на включенні елементів теорії імовірностей до шкільної програми. Перша програма викладання факультативного курсу цього предмету у 1929-1930 н.р. була складена і подана на відгук Остроградському. Відгук був схвальним і Михайло Васильович запропонував ввести цю програму для вивчення у всі математичні школи Росії. Тож з другої половини XIX століття Росія міцно посіла І місце в Європі за рівнем розвитку стохастичних ідей і стала батьківщиною аксіоматичної побудови теорії імовірностей. В Україні вперше курс теорії імовірностей, як факультативний, почав вивчатися у 1966-1967 н.р.

Протягом всієї доповіді на екрані з`являються портрети названих у доповіді математиків.

 

Дуже часто у своєму повсякденному житті ми стоїмо перед вибором: робити, чи ні; брати, чи не брати і навіть не здогадуємося, що інтрига: «повезе – не повезе» може мати математичне пояснення, якщо проаналізувати випадок з точки зору математичної теорії імовірностей. А для цього треба знати основні її поняття. Повторимо? Слайд 23

(фронтальне опитування), відповіді учнів

Теорія імовірностей – це математична наука, яка вивчає закономірності масових випадкових подій.

Випадкова подія – може відбутися, або не відбутися під час масового випробування.

Масові – це події, які можуть бути відтворені необмежену кількість разів.

Попарно-несумісні – якщо жодні дві з них не можуть відбутися разом.

Рівноможливі – події, які не мають переваг одна перед одною.

Вірогідна – подія, яка обов`язково відбудеться.

Неможлива – подія, яка внаслідок випробування не може відбутися.

Імовірність – це числова характеристика можливої появи випадкової події за певної умови.

Формула класичної імовірності

 Взаємонезалежні – події, імовірність яких не залежить від того, які результати має решта випробувань (подій).

Розміщення – це сполуки елементів, які відрізняються одна від одної або самими елементами, або їх порядком, або тим і іншим.

Перестановки – це сполуки, які відрізняються тільки порядком елементів. Р(п) = п!

Комбінації – це сполуки, які відрізняються одна від одної принаймні одним елементом.

Сполуки з повтореннями – це сполуки (розміщення, перестановки, комбінації) в яких елементи повторюються. Наприклад, сукупність букв у слові «математика» це сполука з 6 букв, в якій буква «а» повторюється 3 рази, букви «м» і «т» - по 2 рази.

Які ви знаєте теореми ймовірностей подій? (додавання несумісних подій, множення незалежних подій, теорема про здійснення принаймні однієї з незалежних подій).

 

Добре, але знати теоретичний матеріал в математиці – це пів роботи, а от визначити, якою формулою чи властивістю, або теоремою скористатися – це майже зроблена задача. У завданнях ЗНО і у пробному тестуванні обов`язково є задачі з комбінаторики та теорії імовірностей. Я їх вибрала з тестів 2007-2011 років. Спробуйте лише за умовою задачі вказати, про які сполуки тут йдеться і які формули чи теореми треба використати для розв`язання задачі.

(Умови задач з`являються на екрані, учні пояснюють, яку властивість і чому мають використати для розв`язання) Слайди 24-29

1. З натуральних чисел від 1 до 30 учень навмання називає одне. Яка ймовірність того, що це число є дільником числа 30? (класична імовірність)

 

2. До складу української Прем`єр-ліги з футболу входить 16 команд. Упродовж сезону кожні 2 команди грають між собою 2 матчі. Скільки всього матчів буде зіграно за сезон? (комбінація 2 із 16)

 

 

3. Студенти однієї з груп під час сесії повинні скласти 5 іспитів. Заступнику декана потрібно призначити складання цих іспитів на 5 визначених дат. Скільки всього існує різних варіантів розкладу іспитів для цієї групи? (перестановки)

 

4. На полиці знаходиться 18 однакових скляних банок із джемом. Серед них 6 банок з абрикосовим джемом і 12 з яблучним. Джеми однакові за кольором. Господиня навмання взяла 1 банку. Яка імовірність того, що вона буде з абрикосовим джемом? (класична імовірність)

 

 

5. Кодовий замок на дверях має 10 кнопок, на які нанесено 10 різних цифр. Щоб відчинити двері, треба одночасно натиснути дві кнопки, цифри на яких складають код замка. Скільки всього існує різних варіантів коду? (комбінація 2 з 10)

 

6. Є картки з цифрами: 3, 4, 5, 6,7. Три з них вибирають навмання. Яка ймовірність того, що з вибраних карток можна створити арифметичну прогресію? (класична імовірність)

 

Тепер перевіримо ваше вміння розв`язувати задачі. Оголошується самостійна робота. 6 груп по 4 чоловіки виконують самостійну роботу (2 варіанти по 3 задачі, команда отримує один варіант). Слайд 30

У цей час присутнім гостям пропонується для перегляду фільм «Проблема Монті Хола».

 

 

По закінченні фільму команди обмінюються листочками з відповіями самостійної роботи для перевірки результатів.

На екрані висвічуються тексти самостійної роботи Слайди 31-32

 

Самостійна робота

І варіант

1. Скільки елементарних подій сприяє тому, що сума двох навмання взятих одноцифрових чисел дорівнює 12? (3)
2. Статистики підрахували, що на 20 зупинок токарного верстата на одному із заводів припадає 10 зупинок через заміну різця, 3 – через поломку провода, 2 – через несвоєчасну подачу заготовок. Решта зупинок відбувається з інших причин. Знайти статистичну імовірність зупинки верстата з інших причин. (0,25)
3. Скільки різних прямих можна провести через 9 даних точок площини, з яких жодні 3 не лежать на одній прямій? (36)

 

ІІ варіант

1. Скільки елементарних подій сприяють тому, що навмання вирваний листок з нового календаря містить число 31? (7)
2. Зроблено 100 підкидань грального кубика. Число 2 випало 18 разів, число 4 – 16 разів, число 6 – 20 разів. Знайти статистичну імовірність «випало непарне число». (0,46)
3. Скільки існує способів вибору старости та заступника у вашому класі? (552)

 

Учні по 1 від кожної команди пояснюють свої розв`язки. Решта команд при необхідності задають питання опонентам. (виставляють оцінки на листочках)

Слайд 33

Людина по своїй суті азартна і ми в житті чекаємо неймовірного чуда, а друзям бажаємо удачі. Ми із задоволенням беремо участь у конкурсах з призами, розіграшах і найбільшу насолоду отримуємо, коли щось виграємо чи дістаємо в подарунок. Які ви знаєте прийоми для здійснення чуда? (лотерея). Я прошу всіх присутніх підняти руки, хто хоч раз у житті купляв лотерейний квиток. А хто виграв по ньому? Серед нас таких небагато, бо імовірність виграшу в лотереї дуже мала. Давайте в цьому переконаємось, розв`язавши задачу.

Слайд 34

Задача. У лотереї 1000 білетів, із них на один білет припадає виграш 5000 грн, на 10 білетів – виграш по 1000 грн, на 50 білетів – виграш по 200 грн, на 100 білетів – виграш по 50грн. Решта білетів – невиграшні. Знайдіть імовірність того, що ви, купивши один білет, виграєте не менше 200грн.

 

Розв`язання. Позначимо події: А – виграш не менше 200 грн, А₁ – виграш 200 грн, А₂ – виграш 1000 грн, А₃ – виграш 5000 грн. всі події несумісні, тому можна застосувати теорему суми несумісних подій:

Р(А) = Р(А₁) + Р(А₂)  + Р(А₃) 

Оскільки поява подій виграшу 200 грн дорівнює 50 із 1000 можливих, виграш 1000 – 10 із 1000, виграш 5000 – 1 із 1000, то імовірності цих подій відповідно дорівнюють 0,05, 0,01 і 0,001. За теоремою додавання дістанемо:

Р(А) = 0,05+0,01+0,001=0,061 і становить всього 6% із 100%. (висновок)

 

Якби ми поклалися лише на удачу, то вважали б, що імовірність нашого виграшу вища. Могли також розв`зати задачу неправильно і отримати неймовірний результат, наприклад такий, як у наступній задачі – парадоксі.

Слайд 35

Задача(софізм) про стрільців. Один стрілець дає 80% влучення в ціль, другий – 70%. Знайдіть імовірність влучення в ціль при одночасному пострілі обох одразу.

Розв`язання записане так: Р(А+В) = Р(А) + Р(В) = 0,8+0,7=1,5. Де помилка в міркуваннях?

-дістали хибну відповідь, бо застосували теорему про ймовірність суми несумісних подій там, де її використовувати не можна. Події А та В – сумісні, бо можливо, що обидва стрільці влучать у ціль.

 

А як же правильно розв`язати таку задачу? Давайте розв`яжемо її експерементально.

Складемо умову  задачі разом. Для цього мені потрібно вибрати із класу двох стрільців (за знаком гороскопа). Я вручаю їм по 10 дротиків і даю можливість стріляти по мішенях. Тепер визначаємо імовірність попадання в мішень кожного стрільця.

 

Задача. Яка імовірність того, що при одночасному пострілі по мішені відбудеться принаймні одне попадання?

 

Розв`язання. Стрільці стріляють незалежно один від одного, тому події попадання їх у мішень – незалежні. Позначимо ці події буквами. А – влучення в ціль першого стрільця, В – влучення другого, С – влучення в ціль.

Подію С можна подати у вигляді суми трьох відповідних подій:

С = АВ+АВ+АВ, де АВ – подія, яка полягає в тому, що перший влучив, а другий – ні, подія АВ – другий влучив, а перший – ні, АВ – влучили обидва. Кожний із доданків суми є добутком двох незалежних подій, а тому для обчислення їх імовірностей можна застосувати теорему множення, а для обчислення імовірності події С – теорему додавання:

Р(С) = Р(АВ) + Р(АВ) + Р(АВ) = Р(А)Р(В)+Р(А)Р(В)+Р(А)Р(В). підставимо знайдені дані і обчислимо шукану імовірність.

Слайд 36

А тепер проведемо дослід:

Перед початком уроку я попросила вас, аби кожен на окремих листочках написав по 4 будь-які слова і заготовив по 3 такі листочки, на кожному листку підрахував кількість букв у кожному слові і числом у рамці записав кількість слів з парним числом букв. Здайте, будь ласка листочки моїм асистентам. Я прошу підрахувати кількість записок, що мають у рамці числа 0, 1, 2, 3, 4 (окремо). Тепер повідомте присутнім свої підрахунки. Показую свої результати, зроблені попередньо, знаючи тільки кількість учнів, які будуть на уроці. Пояснюю, як мені це вдалося, використовуючи заготовки на плакаті.

 

Так, теорія імовірностей – наука приблизна, але вона часто дає відповідь там, де, здавалося б розумної позитивної відповіді дати неможливо. Для прикладу приведу задачу з науки генетики.

 

Задача. Молода мати була дуже збентежена, коли дізналася, що її новонароджений син має IV групу крові. «Не може бути, - запевняла вона, - у мене ІІІ група, у чоловіка – ІІ. Або це помилка, або мені підмінили дитину!» Чи може таке бути і з якою імовірністю?

 

Розв`язання. Група крові – спадкова ознака, яка залежить від одного гена. Цей ген має три алелі (ви це вже знаєте), які позначаються символами А, В, О. люди з генотипом ОО мають І групу крові, з генотипом АА і АО – ІІ групу, ВВ і ВО – ІІІ групу, АВ – IV групу. Розглянемо всі можливі випадки.

Слайд 37

(таблиця випадків висвічується на екрані)

 

	А	А	А	О
В	ВА	ва	ва	во
В	ва	ва	ва	Во
В	ва	ва	ва	Во
О	оа	оа	оа	оо

 

 

Усіх можливих випадків – 16, кількість випадків, які сприяють появі крові IV групи (m = 9).

Р(А) = .

 

Якщо ми вже заговорили про теорію імовірностей в генетиці, то я пропоную вашій увазі задачу, яку склала ваша однокласниця Юрченко Алла.

 

Задача. Блакитнооких людей на планеті багато, карооких – ще більше, а от людей з очима різного кольору – зовсім мало. Я хочу, аби ми разом вирахували, яка імовірність народження у обох блакитнооких батьків дитини з очима блакитного і зеленого кольору

 

 

Слайд 38

Розв`язання.

Ця задача, так як попередня, за законом Менделя не розв`язується, бо імовірність народження дитини з очима різного кольору є генетичним відхиленням (соматичне відхилення), проте імовірність народження у пари блакитнооких батьків дитини з блакитними очима дорівнює 0,99, а із зеленими – 0,01. Оскільки поява різних очей розглядається як сума сумісних подій (різні очі один одному не заважають), то імовірність цієї події дорівнює добутку сумісних подій, тобто 0,990,01=0,0099. У цій парі розглядається по одному окові відповідного кольору, тому ділимо знайдену відповідь на 2. Маємо результат: ,00992=0,004950,005 (5 із 1000, або 2 із 200 пар батьків можуть дочекатися такого чуда).

Як бачите, така імовірність мізерна. І дісталася ця особливість – мені.

Слайд 39

Ще одну задачу (домашнє завдання) підготував Василенко Богдан

Давайте розв`яжемо її.

 

Задача. Ілля Муромець зупинився перед каменем на роздоріжжі трьох доріг. Напис на камені був такий: «Поїдеш наліво – загинеш з імовірністю 0,5; направо – з імовірністю 0,7; прямо – з імовірністю 0,6. Підкинь монету двічі: випаде два герби – їдь наліво, дві цифри – направо, а якщо герб і цифра – прямо». Яка ймовірність того, що дочекаються Іллю його друзі – Добриня та Альоша?

Розв`язання. (колективне, виступаючий задає запитання, учні відповідають і разом виконують під запис задачу.)

Нехай імовірнісний простір побудовано так, що серед подій є події: Н₁ – «Ілля поїхав наліво», Н₂ – «Ілля поїхав направо», Н₃ – «Ілля поїхав прямо», А – «Ілля залишився живий» (а тому друзі його дочекалися). Очевидно, що Н_1, Н_2, Н₃  - гіпотези. З умови задачі випливає, що

 

Р( Н₁)= ,   Р(Н₂)= , Р(Н₃)=,  імовірність того, що він поїде наліво і залишиться живим дорівнює 1 - 0,5 = 0,5, поїде направо і залишиться живим дорівнює 1 – 0,7 = 0,3, поїде прямо і залишиться живим дорівнює

1 – 0,6 = 0,4. За формулою повної імовірності маємо:

Р(А) = × 0,5 + × 0,3 + × 0,4 = 0,4

 

Для того, щоб зайвий раз переконатися, що наука «теорія імовірностей» - експерементальна, проведемо експеримент і розв`яжемо ще одну задачу.

 

Задача. Перед вами на столах знаходяться комплекти із шахових дошок і різнокольорових шахових тур. Треба розмістити 2 тури різного кольору на дошці так, щоб кожна могла взяти іншу. Скільки існує таких розміщень?

 

Розв`язання.  Учні розміщують тури, переконуються, що розміщення різних команд – різне. Пояснюють спосіб розв`язання задачі, враховуючи правила шахової гри. Оголошують відповідь (14×64)

 

 

На закінчення уроку хочу привести вам ще один софізм.

Взвод крокує по плацу «правою-лівою» на «раз-два» з частотою два кроки в секунду. Ви спостерігаєте, скажімо 100 кроків і обчислюєте частоту, з якою взвод крокує правою. Отримуєте ½. Нічого парадоксального. А давайте спробуємо обчислити частоту, з якою взвод крокує правою, спостерігаючи не кожні пів секунди, а кожну секунду. Отримуємо щось дивне. Частота кроків правою дорівнює 100 із 100, тобто 1, або 100%, а частота кроків лівою при цьому дорівнює нулю. Начебто ці солдати взагалі крокують тільки правою ногою. У чому річ?

 

Підводимо підсумки уроку.

Слайд 40

Домашнє відеозавдання. Фільм (де дівся  долар?) демонструється на екрані.

 

На уроці розглянуто задач: усно – 6

                                            розв`язано, включаючи софізми – 14.