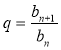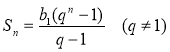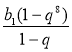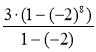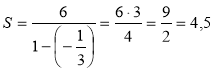Методичні рекомендації по самостійному вивченню або узагальненню теми "Геометрична прогресія"

Про матеріал

Перегляд файлу

План заняття

Тема: Геометрична прогресія. Формула n-го члена та суми n членів. Нескінченна спадна геометрична прогресія.

Геометричною прогресією називається послідовність відмінних від нуля чисел, кожний член якої, починаючи з другого, дорівнює попередньому, помноженому на те саме число (знаменник геометричної прогресії).

Приклад. 3; 9; 27; 81; 243; ... — геометрична прогресія, бо а₂= а₁∙ 3; а₃= а₂ ∙ 3; а₄= а₃∙ 3; ... . (3 — знаменник цієї прогресії).

Рекурентна формула геометричної прогресії

Якщо (b_п) — геометрична прогресія, то b_n+1 = b_n·q, де b_п — п-й член; q — знаменник геометричної прогресії.

З рекурентної формули випливає:

Властивості геометричної прогресії:

а) для кожного члена геометричної прогресії, починаючи з другого: —характеристична властивість;

б) якщо (b_п) — скінченна геометрична прогресія, то

b₁∙ b_n= b₂ ∙ b_n-1 = b₃ ∙ b_n-2 = const (b₁ і b_n — крайні члени цієї прогресії).

Формула п-го члена геометричної прогресії

Якщо (b_n) — геометрична прогресія, то b_n=b_l· q^n-¹,де b₁ — перший член геометричної прогресії; q — знаменник геометричної прогресії.

Приклад 1. Знайдемо шостий член геометричної прогресії (b₁): ; 1; 5; ... .

Розв'язання

b₁= ; b₂=1; q = = 5; b₆= b₁∙ q⁵ = ∙ 5⁵= 5⁴= 625.

Відповідь: 625.

Приклад 2. Знайдемо перший член геометричної прогресії (b_п), якщо b₇= 32; q = -2.

Розв'язання b₇ = b₁ ∙ q⁶ b₁ = = = .

Відповідь: .

Приклад 3. Знайдемо знаменник геометричної прогресії (b_n), у якої b₇= -12, b₉= -108.

Розв'язання

b₉= b₁ ∙ q⁸; b₇= b₁∙ q⁶ = q²; q² = = 9, тоді q = 3 або q = -3.

Відповідь: 3 або -3.

Формули суми перших п членів геометричної прогресії

Якщо (b_п) — геометрична прогресія, q — її знаменник, a S_n — сума перших п її членів, то:

(1)

або (2)

! Зауваження: якщо q = 1, то S_n= b₁∙n (b₁= b₂ =... = b_n).

Приклад 1. Знайдемо суму перших восьми членів геометричної прогресії

(b_n): 3; -6; 12; ... .

Розв'язання

Маємо b₁= 3, q = = -2, тоді за формулою (2):

S₈= = = = -255.

Відповідь: -255.

Приклад 2. Знайдемо перший член геометричної прогресії (b_п), якщо її четвертий член утричі більший за третій, а сума перших п'яти членів дорівнює -12,1.

Розв'язання

Оскільки b₄= 3b₃, то q = 3. За умовою S₅= -12,l, тому, оскільки , тобто ; -12,1 = ; -12,1 = 121b₁; b₁= -0,1.

Відповідь: -0,1.

Нескінченна геометрична прогресія - це геометрична прогресія , у якої | q | < 1

Приклади:

а) 1; ; ; ; ... q = , | q | < 1;

б) 3; ; ; ... q = , | q | < 1;

в) 100; 10; 1; ; ... q = , | q |< 1;

г) 32; 0,32; 0,0032; ... q = , | q | < 1.

Якщо (b_n) — нескінченна геометрична прогресія, у якої | q | < 1, то сума всіх її членів S обчислюється за формулою

Приклад 1. Знайдемо суму нескінченної геометричної прогресії (b_n): 6; -2; ... .

Розв'язання

За умовою b₁ = 6; b₂ = -2, отже, q = = . Маємо геометричну прогресію, у якої | q | < 1. За формулою знаходимо:

Відповідь; 4,5.

Приклад 2. Запишемо число 0,(7) у вигляді звичайного дробу.

Розв'язання

Запис 0,(7) означає нескінченний періодичний дріб 0,7777....

Його можна подати як нескінченну суму + + + … .

Доданки цієї суми є членами нескінченної геометричної прогресії, у якої

b₁= , q = : = , | q | < 1. Тоді ця сума дорівнює:

. Тому 0,(7) = .

Відповідь: .

Усні вправи

№1. За означенням перевірте, чи є геометричною прогресією послідовність:

а) 1; 2; 4; 8; 16; ...; ( так бо q=2)

б) 1; 8; 27; 64; ... . (ні)

№2. Укажіть перший член та знайдіть знаменник геометричної прогресії:

1) 1; -5; 25; ...; 2) -6; -6; -6; ...; 3) 9; 3; 1; ...;

4) 7; ; ; ...; 5) -3; 3; -3; ... .

№3. Знайдіть другий і третій члени геометричної прогресії (b_п), якщо:

1) b₁= 3, q = 2; 2) b₁ = 5, q = -1.

Відповідь: 1) b₂= 6 b₃= 12 2) b₂= - 5 b₃= 5

Тестові завдання

№1. Яка з наведених послідовностей є геометричною прогресією?
а) 4; 8; 32; 64; б) 80; 40; 20; 5; в) 2; 6; 18; 54; г) 2; -10; 50; 250.

Відповідь: в) 2; 6; 18; 54 бо q=

№2. Знайдіть знаменник геометричної прогресії (b_п), якщо b₅= , b₆= .

а) ; б) ; в) ; г) .

(Відповідь: б) бо = )

№3. Дев'ятий член геометричної прогресії дорівнює 12, а знаменник дорівнює 3. Знайдіть десятий член геометричної прогресії.

а) 15; б) 36; в) 39; г) 108.

(Відповідь: b₁₀= b₉q=123 = 36)

Розв’язання письмових вправ

№1. Дана геометрична прогресія (b_п). Знайдіть b₃, якщо:

1) b₄= 7, q = -0,1

b₄= b₃q

b₃= =

2) b₆= 1, b₅= 2

q = =

b₅= b₁

2 = b₁ 2 = b₁ b₁ = 216 = 32

3) b₂= 0,2, b₄= 5

1 спосіб:

b₂ b₄= 0,25 = 1, b₃= 1 (властивість)

2 спосіб:

b₄= b₂

5 = 0,2 = q= b₃= = = 1

№2. Дана геометрична прогресія, у якої q =3, b₆ = 486. Знайти b₁ .

b₆= b₁

486 = b₁

486 = b₁243

b₁ = 2

Відповідь:2

№3.

1) Між числами 2,5 та 20 вставте два числа так, щоб вийшла геометрична прогресія.

2,5 __ __ -20

b₁ b₂ b₃ b₄

b₄= b₁

-20 = 2,5

= - 8

q= -2

Відповідь: 2,5 -5 10 -20

2) Між числами 5 і 405 вставте три числа так, щоб вийшла геометрична прогресія. Запишіть цю прогресію.

5 __ __ __ 405

b₁ b₂ b₃ b₄ b₅

b₅= b₁

4055 = 5

У відповіді дві прогресії:

5 15 45 135 405 та

5 -15 45 -135 405

№4. Дана геометрична прогресія, у якої S₆= 63 q = -2. Знайти b₁.

S_n = S₆ =

63 =

63 = -21 b₁

b₁ = -3

Відповідь: -3

№5. Дана геометрична прогресія, у якої b₁=8, b₆ = 0,25. Знайти q та S₇.

b₆= b₁

0,25 = 8

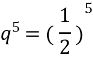
q =

S₇ =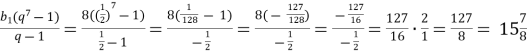

Відповідь: q = ; S₇ =

№6. Дана нескінченна спадна геометрична прогресія 125; -25; 5; … Знайти суму цієї прогресії.

b₁ = 125 b₂ = - 25 q =

S = =

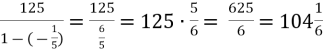
Відповідь:

№7. Знайти q нескінченної геометричної прогресії (b_n), якщо

b₁ = 54, S=81.

S =

81 = 1 – q = 1 – q = q =

Відповідь:

Самостійна робота

№	В -1	В - 2
1	Знайдіть перші чотири члени геометричної прогресії (b_n), якщо b₁ = -2, q = -3.	Знайдіть перші чотири члени геометричної прогресії (b_n), якщо b₁ = 25, q = - 0,2.
2	Знайдіть знаменник і 5-й член геометричної прогресії -72; 12; -2; ... .	Знайдіть знаменник і 5-й член геометричної прогресії ; , , ... .
3	Між числами 3 та 729 вставте чотири таких числа, щоб разом із даними числами вони утворювали геометричну прогресію.	Між числами 64 і 27 вставте два таких числа, щоб разом із даними числами вони утворювали геометричну прогресію.
4	Дана геометрична прогресія, у якої S₆= 63 q = -2. Знайти b₁.	Дана геометрична прогресія, у якої S₅= 217 q = 2. Знайти b₁.
5	Дана нескінченна спадна геометрична прогресія, у якої q = , S = -81. Знайти b₄.	Знайти b₄ нескінченної геометричної прогресії (b_n), якщо b₁ = 54, S=81.