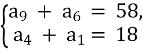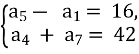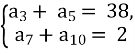Методичні рекомендації по самостійному вивченню або узагальненню теми "Арифметична прогресія"
Тема: Поняття послідовності. Задання послідовності. Арифметична прогресія. Формула n-го члена та суми n членів арифметичної прогресії.
|
Числовою послідовністю називається функція, яка задана на множині всіх натуральних чисел або на множині перших n натуральних чисел. |
|||||||
|
Числова послідовність позначається так: (аn): а1; а2; а3; ...; аn. Кожне число аn — n-й член послідовності; n — номер члена. |
|||||||
|
Види числових послідовностей |
|||||||
|
1. Якщо кількість членів п послідовності (аn) скінченна, то (аn) — скінченна послідовність. Якщо кількість членів п послідовності (аn) нескінченна, то (аn) — нескінченна послідовність. Приклади: а) послідовність (аn) натуральних чисел нескінченна; б) послідовність (аn) коренів рівняння (х – 1)(х – 2)(х + 3) = 0 скінченна. |
|||||||
|
2. Якщо кожний наступний член послідовності, починаючи з другого, більший за попередній, то послідовність є зростаючою. Якщо кожний член послідовності, починаючи з другого, менший від попереднього, то послідовність є спадною. |
|||||||
|
Приклади: а) (аn): 1; 2; 3; ... — послідовність натуральних чисел є зростаючою; б) (bn): -1; -2; -3; ... — послідовність цілих від'ємних чисел є спадною. |
|||||||
|
Способи задання числових послідовностей: 1) описом знаходження її членів. Приклад. Числова послідовність дільників числа 15, записаних у порядку зростання: (аn): а1= 1; а2 = 3; а3 = 5; а4 = 15 |
|||||||
|
2) переліком її членів. Приклад. (an): 54; 1; 33; 27, тоді а1 = 54; а2 = 1; а3 = 33; а4 = 27 |
|||||||
|
3) таблицею. Приклад. |
|||||||
|
|
n |
1 |
2 |
3 |
4 |
5 |
|
|
|
аn |
-2 |
1 |
-4 |
1 |
- 6 |
|
|
|
|||||||
|
Тоді а1 = -2; а2 = 1; а3 = - 4; а4 = 1; а5 = - 6; |
|||||||
|
4) формулою n-го члена. Приклад. аn = n2 – 1, тоді а1 = 12 – 1 = 0; а2 = 22 – 1 = 3; а3 = 32 – 1 = 8 і т.п.; |
|||||||
|
5) рекурентною формулою. Приклад. аn = аn-1 ∙ аn-2, якщо а1 = 1; а2 = 2, тоді а1 = 1; а2 = 2; а3 = а1 ∙ а2 = 2; а4 = а2 ∙ а3 = 2 ∙ 2 = 4; а5 = а3 ∙ а4 = 4 ∙ 2 = 8. |
|||||||
|
Сума перших п членів арифметичної прогресії |
|||||||
|
1. Якщо a1 і an — перший і n-й члени арифметичної прогресії (аn), то сума Sn перших п членів цієї прогресії дорівнює:
|
|||||||
|
2. Якщо a1 і d — перший член і різниця арифметичної прогресії (аn), то сума Sn перших n її членів дорівнює:
|
|||||||
|
Приклад. Знайдемо суму перших десяти членів арифметичної прогресії (аn), у якої: 1) a1 = 10, а10 = -10; 2) а1 = 2, d = -3. Розв'язання |
|||||||
|
1) S10 = |
|||||||
|
2) S10 = = -23 ∙ 5 = -115. Відповідь: 1) 0; 2) -115. |
|||||||
|
Властивість членів арифметичної прогресії |
|||||||
|
an = Приклад. (аn): ___ ___ 190 ___ 218 ___ Знайдіть невідомі члени арифметичної прогресії а3 = 190 а5 = 218
а4 = а6 = 218 + 14 = 232 а2 = 190 – 14 = 176 а1 = 176 – 14 = 162 (аn): 162 176 190 204 218 232
|
|||||||
Закріплення знань
1 рівень
№1.
Дано послідовність: 0,1; 7; 0,2; 8; 0,3; 9. Укажіть:
|
6 |
|
0,2 |
|
5 |
|
0,3 0,1 |
№2. Послідовність (хn) задано формулою хn = n + 5. Укажіть перші три члени цієї послідовності. Чи є ця послідовність зростаючою? нескінченною?
Відповіді: х1 = 1 + 5 = 6
х2 = 2 + 5 = 7
х3 = 3 + 5 = 8
(хn): 6 7 8 9 10 11 - зростаюча (d =1![]() ) та нескінчена
) та нескінчена
№3. Знайдіть четвертий член і різницю арифметичної прогресії:
|
умова |
а1 |
а2 |
d |
яка |
а4 |
|
1) 2; 7; 12; |
2 |
7 |
7 – 2 = 5 |
зростаюча |
а4 = а3+ d =12+5 =17 |
|
2) 6; 5,5; 5; |
6 |
5,5 |
5,5 – 6 = - 0,5 |
спадна |
5 – 0,5 = 4,5 |
|
3) -9; -7; -5; |
-9 |
-7 |
-7 - (-9) = 2 |
зростаюча |
- 5 + 2 = - 3 |
|
4) -10; -15; -20 |
-10 |
-15 |
-15 - (-10)= -5 |
спадна |
- 20 – 5 = - 25 |
№4. Знайдіть невідомі для арифметичної прогресії (ап), у якої:
1) a1 = -2, d = 4, а7 - ?
а7 = а1 + 6d = -2 + 6![]() 4 = -2 + 24 = 22
4 = -2 + 24 = 22
2) a40 = 100, а1 = - 368, d - ?
а40 = а1 + 39d
100 = - 368 + 39d
39 d = 468
d= 12
3) а12 = 23 d= 3, а1 - ?
а12 = а1 + 11d
23 = а1 + 11![]() 3
3
23= а1 + 33
а1 = -10
№5. Між числами 7 та 35 вставте шість чисел так, щоб вийшла арифметична прогресія. Запишіть цю прогресію.
7 _ _ _ _ _ _ 35
а1 а2 а3 а4 а5 а6 а7 а8
а1 = 7 a8 = 35
а8 = а1 + 7d
35 = 7 + 7![]()
7 d = 28
d=4
(ап): 7 11 15 19 23 27 31 35
№6. В арифметичній прогресії (ап) а1 = 1, d = 4. Знайдіть а8, S10.
а8 = а1 + 7d = 1 + 7![]() 4 = 29
4 = 29
S10= ![]() = (2
= (2![]() 1 + 9
1 + 9![]() 4)
4)![]() 5 = (2 + 36)
5 = (2 + 36)![]() 5 =38
5 =38![]() 5 = 190
5 = 190
№7. Знайти номер члена арифметичної прогресії, який дорівнює 214, якщо
(ап) : 6; 14; 22; …?
а1 = 6 d = 8
аn = а1 + d(n – 1)
214 = 6 + 8(n – 1)
214 = 6 + 8n – 8
8n = 216
n = 27
№8. Знайти перший член арифметичної прогресії, якщо d = 2, S4 = 10.
n = 4
S4= ![]() = (
= (![]()
10 = 2![]() (2а1 +3
(2а1 +3![]() 2)
2)
5 = 2а1 + 6
2а1 = - 1
а1 = - 0,5
№9. Знайти а1, d якщо а2 + а5 = 19, а6 + а3 = 13.
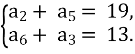
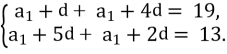 -
- 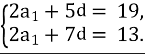
- 2d = 6
d = - 3
![]()
2а1 = 19 + 15
а1 = 17
№10. Знайти суму 20 членів арифметичної прогресії, якщо а1= 5 а11 = 110.
а11 = а1 + 10d
110 = 5 + 10d
10d= 105
d = 10,5
S20 = ![]()
S20 = (![]()
2 рівень
№11. Перший член арифметичної прогресії дорівнює 12, а її різниця -2. Скільки треба взяти перших членів прогресії, щоб їх сума дорівнювала - 48?
а1 = 12 d = -2 Sn = - 48 n - ?
Sn= ![]()
- 48 = ![]()
-48![]() 2 =
2 = ![]()
-96 = 24![]()
2![]() - 2
- 2![]()
![]() - 13
- 13![]()
![]()
![]() 2 = -3
2 = -3 ![]() (не може бути)
(не може бути)
№12. Скільки додатних членів містить арифметична прогресія 40; 37; 34;…?
а1 = 40 d = - 3 додатні, це аn ![]()
аn = а1 + d(n – 1) тобто
а1 + d(n – 1)![]()
40 – 3(n – 1)![]()
40 - 3n + 3![]()
- 3n ![]()
n ![]()
n ![]()
n ![]() (номери цілі числа)
(номери цілі числа)
3 рівень (ЗНО)
№13. При якому значенні х задана послідовність є арифметичною прогресією, якщо:
8х – 2; 6х; х2 + 2
1 спосіб:
а1 = 8х – 2
а2 = 6х
а3 = х2 + 2
За властивістю маємо: а2 = ![]()
6х = ![]()
12х = 8х + х2
х2 – 4х = 0
х(х – 4) = 0
х1 = 0
х2 = 4
2 спосіб:
а1 = 8х – 2
а2 = 6х
а3 = х2 + 2
d = а2 - а1 = 6х – (8х – 2) = - 2х + 2
d = а3 – а2= х2 + 2 – 6х
Прирівнюємо: d = d
х2 + 2 – 6х = - 2х + 2
х2 + 2 – 6х + 2х – 2 = 0
х2 – 4х = 0
х(х – 4) = 0
х1 = 0
х2 = 4
У ЗНО буває умова – записати ненульове значення х, тоді відповідь х = 4.
Самостійна робота з теми «Арифметична прогресія»
|
№ |
В -1 |
В - 2 |
В - 3 |
В - 4 |
|
1 |
Знайти а21, якщо а1 = 4, d = 5. |
Знайти а21, якщо а1 = 0,1, d = 0,3. |
Знайти а21, якщо а1 = 5, d = 4. |
Знайти а21, якщо а1 = 0,3, d = 0,1. |
|
2 |
Знайти а1, якщо а41 = 23, d = 5. |
Знайти а1, якщо а91 = 14, d = 2. |
Знайти а1, якщо а36 = 15, d = 4. |
Знайти а1, якщо а26 = 57, d = 3. |
|
3 |
Знайти номер члена арифмет. прогресії, який дорівнює 294, якщо а1 = 102, d = 4. |
Знайти номер члена арифмет. прогресії, який дорівнює 39, якщо а1 = 6,5, d = 1,3. |
Знайти номер члена арифмет. прогресії, який дорівнює 17,2, якщо а1 = 5,3, d = 0,7. |
Знайти номер члена арифмет. прогресії, який дорівнює 316, якщо а1 = 211, d = 15. |
|
4 |
Між числами 1 та 25 вставте п’ять чисел так, щоб вийшла арифметична прогресія. |
Між числами 7 та 35 вставте шість чисел так, щоб вийшла арифметична прогресія. |
Між числами 3 та 45 вставте шість чисел так, щоб вийшла арифметична прогресія. |
Між числами 2 та 32 вставте п’ять чисел так, щоб вийшла арифметична прогресія. |
|
5 |
Знайти S12, якщо а1 = 7, а26 = 62. |
Знайти S12, якщо а1 = 11, а16 = 47. |
Знайти S12, якщо а1 = 14, а6 = 30. |
Знайти S12, якщо а1 = 20, а15 = -16. |
|
6 |
Знайти а1, d якщо
|
Знайти а1, d якщо
|
Знайти а1, d якщо
|
Знайти а1, d якщо
|


про публікацію авторської розробки
Додати розробку