Методичні рекомендації по вивченню таблиці множення на пальцях для дітей з особливими потребами

Слов'янська спеціальна школа № 23 Донецької обласної ради

С.С. Ворошило

Методичні рекомендації

по вивченню таблиці множення на пальцях для дітей з особливими потребами

Слов'янськ 2023

Зміст

Вступ ………………………………………………………………………………………… 3

Особливості викладання математики в корекційних класах ……………………….. 5

Робота з учнями з особливими потребами……………………………………………… 8

Формування інтересу до математики як обов’язкова умова успішного оволодіння математичними знаннями, вміннями та навичками у учнів з особливими потребами……………………………………………………………………………………… 9

Рекомендації по вивченню таблиці множення на пальцях……………………………10

Література ………………………………………………………………………………..…. 12

Вступ

Методика навчання математиці в корекційній школі почала формуватись в нашій країні в 30-ті роки ХХ століття. Основоположники корекційної школи А.Н.Грабаров, Є.В.Герьє, Н.В.Чехов вважали, що математика повинна дати дитині з особливими потребами лише практичні прийоми лічби. Вони стверджували, що навчання математиці повинно бути індивідуалізованим внаслідок різних здібностей дітей, обґрунтовували необхідність використання конкретного матеріалу, який повинен бути добре знайомим і цікавим учням. В перші роки становлення корекційної школи використовувався методичний досвід навчання лічби прогресивних зарубіжних спеціалістів О.Декролі, Ж.Демора, М.Монтесорі, Е.Сегена та ін.

Наприкінці 40-х – на початку 50-х років в спеціальній методиці математики з’явились експериментальні дослідження, присвячені удосконаленню навчання математиці школярів з порушеннями інтелекту, різним розділам математики. Так, у дослідженнях К.А.Михальського, М.І.Кузьмицької, О.П.Смалюги, М.Н.Перової, А.А.Хілько, А.А.Ек, Г.М.Капустіної та ін. розроблена методика навчання вирішенню арифметичних задач, показана роль підготовчих вправ, дидактичних ігор, наочності, а також предметно-практичних вправ, спрямованих на конкретизацію змісту завдань.

Пошукам прийомів розвитку активності й самостійності учнів допоміжної школи в процесі роботи над арифметичною задачею присвячено дослідження А.А.Хілько, а розвитку самостійності при виконанні домашніх завдань – дослідження А.Н.Ляшенко.

Значення й прийоми розвитку мотивації в процесі навчання математиці переконливо показані в дослідженні Ю.Ю.Пумпутіса, який прийшов до висновку, що, коли дії учнів мотивовані, коли вони можуть отримані на уроках математики знання застосувати в своїй побутовій або трудовій діяльності, якість засвоєння математичного матеріалу зростає.

Розвитку пізнавального інтересу до математики сприяє використання дидактичних ігор, цікавих вправ, предметно-практичної діяльності дітей, усвідомлення практичної значимості математичних знань, що було доведено М.Н.Перовою.

С.Дубовським було проаналізовано експериментальні дані та запропоновано конкретну методику розвитку інтересу до математики в учнів допоміжної школи, а також узагальнено практичний досвід вчителів-дефектологів з цього питання. Це мало конкретне практичне значення, оскільки дало можливість сформульовані раніше теоретичні положення застосовувати на практиці.

Аналіз методичних основ викладання математики в корекційній школі дає можливість зробити висновок, що в методиці математики зроблено значні досягнення в пошуках ефективних дидактичних прийомів корекційного навчання математики на основі врахування особливостей діяльності учнів з особливими потребами та засвоєння ними математичних знань, в чому надзвичайно велика роль належить розвитку пізнавального інтересу до математики.

Особливості викладання математики в корекційних класах

Основні задачі спеціальної школи – максимальне подолання недоліків пізнавальної діяльності і емоційно-вольової сфери школярів з особливими потребами, підготовка їх до участі у корисній праці, соціальна адаптація в умовах сучасного суспільства.

При визначенні завдань навчання математики учнів допоміжної школи необхідно виходити з цих конкретних задач.

Досягти оволодіння учнями системою досяжних математичних знань, вмінь та навичок, необхідних у повсякденному житті і в майбутній професії, так міцно, щоб вони стали надбанням учнів на все життя – головна загальноосвітня задача навчання математики.

За період навчання в школі учні повинні отримати наступні математичні знання та практичні навички:

а) уявлення про натуральне число, нуль, натуральний ряд чисел, про звичайні та десятинні дробі;

б) уявлення про основні величини (довжина відрізку, вартість, маса предметів, площа фігур, об’єм, час), одиниці виміру величин та їх співвідношення;

в) знання метричної системи мір, мір часу й уміння практично користуватись ними;

г) навички практичних вимірів, вміння користуватись інструментами (лінійкою, мірною кружкою, вагами, годинником і т.д.);

д) вміння виконувати чотири основні арифметичні дії з багатозначними числами і дробами;

є) вміння вирішувати прості й складні (в 3-4 дії) арифметичні задачі;

ж) уявлення про площинні та об’ємні геометричні фігури, знання їхніх властивостей, побудова цих фігур за допомогою креслярських інструментів (лінійки, циркуля, угольника, транспортира).

Навчаючи математики учнів допоміжних шкіл, треба враховувати, що засвоєння необхідного матеріалу не повинно мати характеру механічного заучування й тренування. Знання, отримані учнями, повинні бути усвідомленими. Від предметної, наочної основи слід переходити до формування доступних математичних понять, вести учнів до узагальнень і на їх основі виконувати практичні роботи.

Математика в допоміжній школі виконує одну з важливих задач навчання учнів з порушеннями інтелекту – подолання недоліків їх пізнавальної діяльності і особистісних якостей.

Математика як навчальний предмет містить необхідні передумови для розвитку пізнавальних здібностей учнів, корекції інтелектуальної діяльності й емоційно-вольової сфери.

Формуючи у учнів з особливими потребами на наочній і наочно-діяльнісній основі перші уявлення про число, величину, фігуру, вчитель одночасно ставить і вирішує в процесі навчання математики завдання розвитку наочно-діяльнісного, наочно-образного, а потім і абстрактного мислення цих дітей.

На уроках математики в результаті взаємодії зусиль учителя та учнів (за направляючого й організуючого впливу вчителя) розвивається елементарне математичне мислення учнів, формуються і коригуються такі його форми, як порівняння, аналіз, синтез, розвиваються здібності до узагальнення й конкретизації, створюються умови для корекції пам’яті, уваги та інших психічних функцій.

В процесі навчання математики розвивається мовлення учнів, збагачується специфічними математичними термінами й виразами їх словник. Учні вчаться коментувати свою діяльність, давати повний словесний звіт про вирішення задачі, виконання арифметичної дії або завдання з геометрії. Все це вимагає від учнів більше відповідальності та усвідомленості своєї діяльності, їхні дії набувають узагальненого характеру, що, безумовно, має величезне значення для корекції недоліків мислення школярів з особливими потребами.

Навчання математики організує й дисциплінує учнів, сприяє формуванню таких рис особистості, як акуратність, наполегливість, воля, виховує звичку до праці, бажання працювати, вміння доводити будь-яку справу до кінця.

На уроках математики в процесі виконання практичних вправ (ліплення, обвідка, штриховка, розфарбовування, вирізання, наклеювання, конструювання та ін.) коригуються недоліки моторики дитини.

Навчання математики в спеціальній школі сприяє вирішенню й виховних завдань. Матеріал арифметичних задач, завдань з нумерації та з інших тем містить відомості про розвиток промисловості, сільського господарства, будівництва в нашій країні. Це розширює світогляд учнів, сприяє вихованню любові до Батьківщини.

Підготовка учнів до життя, трудової діяльності є однією з найбільш важливих задач навчання. Курс математики повинен дати учням такі знання й практичні вміння, які допоможуть краще розпізнати у явищах довколишнього життя математичні факти, застосовувати математичні знання до вирішення конкретних практичних завдань, які повсякденно ставить життя. Опанування вмінь лічби, усних та письмових обчислень, вимірювань, вирішення арифметичних задач, орієнтації в часі та просторі, розпізнавання геометричних фігур дозволять учням більш успішно вирішувати життєво-практичні задачі.

Робота з учнями з особливими потребами

Враховуючи наявність у багатьох дітей з особливими потребами стійкого негативного ставлення до процесу навчання взагалі і до математики зокрема, намагатися створити в учнів відчуття стабільних успіхів. На невдачі, помилки, труднощі увага майже не повинна звертатись. Учитель постійно наголошує на успіхах як особисто кожного учня, так і колективу в цілому. Спеціально відзначається позитивна тенденція не тільки у засвоєнні знань, а й у прагненні до цього переважної більшості дітей. Основною метою такого заходу є відродження та закріплення віри учнів у власні сили.

Особливе пожвавлення в класі викликають інсценовані математичні гуморески. Наприклад:

Перший учень: Скільки тобі років?

Другий: Одинадцять.

Перший: Так ще минулому тобі було п’ять!

Другий: А в цьому вже шість. А разом – одинадцять.

*       *       *

Перший учень (батько): Сходи, синку на базар, купи на одну гривню яблук. Попроси продавця вибрати добрі, це ж для гостей.

Другий (ведучий): Приносить Петро яблука.

Третій учень (Петро): Тату! Жодного поганого!

Батько: А звідки ти знаєш?

Петро: Так я кожне покуштував.

Таким чином створюється загальний позитивний настрій класу й кожного учня зокрема, що стимулює учнів до занять математикою й пробуджує їхній інтерес до предмету.

Формування інтересу до математики як обов’язкова умова успішного оволодіння математичними знаннями, вміннями та навичками у учнів з особливими потребами.

Оволодіння навіть елементарними математичними поняттями вимагає від дитини достатньо високого рівня розвитку таких процесів логічного мислення, як аналіз, синтез, узагальнення, порівняння.

Спеціальні дослідження В.А.Крутецького показали, що для творчого оволодіння математикою як навчальним предметом необхідна здатність до формалізованого сприйняття математичного матеріалу (схоплення формальної структури задачі), здатність до швидкого й широкого узагальнення математичних об’єктів, відношень, дій, здатність мислити згорнутими структурами (згортання процесу математичного розмірковування), гнучкість процесів мислення, здатність до швидкої перебудови напряму розумового процесу, математична пам’ять (узагальнена пам’ять на математичні відношення, методи вирішення задач, принципи підходу до них).

Саме ці здатності, необхідні для успішного оволодіння математичними знаннями, у учнів допоміжної школи розвинуті надзвичайно слабко. Відомо, що математика є одним з найбільш складних предметів для цієї категорії учнів. З одного боку, це пояснюється абстрактністю математичних понять, а з іншого, особливостями засвоєння математичних знань учнями.

Ускладнення в засвоєнні навчального матеріалу учнями допоміжної школи нерідко призводять до зниження їхнього інтересу до навчання. Особливо складним предметом стає арифметика.

Для успішного навчання й виховання дітей з особливими потребами необхідно в перші ж роки шкільного навчання розбудити їх інтерес до навчальних занять, зацікавити, мобілізувати їхню увагу, активізувати пізнавальну діяльність.

Вчителі допоміжної школи використовують з цією метою різноманітні методи й прийоми викладання арифметики, використовуючи яскравий дидактичний матеріал і наочні посібники, чим викликають у учнів практичний інтерес до процесу оволодіння предметом.

Рекомендації по вивченню таблиці множення на пальцях

Старовинний спосіб обліку на пальцях простий, створений матінкою природою.

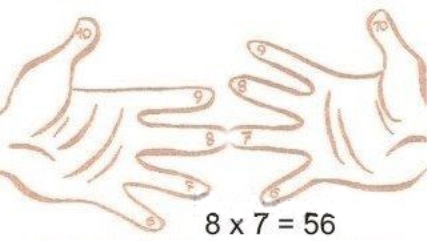
Для цього треба пронумерувати пальці на обох руках. Мізинець – 6, палець без ім’я – 7, середній – 8, вказівний – 9, великий – 10 (на це він і великий, щоб висловити найбільше число). Скажімо, ви хочете знати, скільки буде 8 х 7. З’єднайте разом середній палець лівої руки (8) з пальцем без ім'я (7), як показано на малюнку.

А тепер підрахуємо. Два з’єднаних пальця додати до тих, які знаходяться під ними, вкажуть на кількість десятків. У цьому випадку – 5, а кількість пальців над з’єднаними лівої  та правої руки перемножити. У нашому випадку, 2 х 3 = 6. Це число одиниць у зразку. Десятки додаємо до одиниць і отримаємо відповідь – 56.

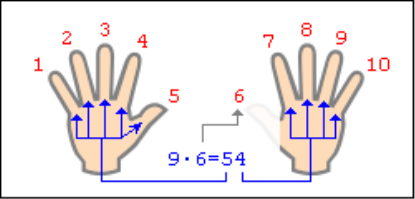
Техніка множення числа 9, досить легко виконується на пальцях. Для цього треба розсунути пальці на обох руках і повернути долонями від себе. Розумово привласнити пальцям послідовно числа від 1 до 10, починаючи з мізинця лівої руки.

Припустимо, треба помножити 9 на 6. Для цього треба загнути палець, рівний числу, на яке треба помножити дев’ятку, у нашому випадку палець з номером 6. Кількість пальців, які залишились ліворуч від загнутого, показує кількість десятків у відповіді, а кількість пальців праворуч – кількість одиниць. Ліворуч у нас залишається 5 пальців, а праворуч – 4, тобто відповідь буде  - 54.

Література:

1. Сак Т. Застосування зразка у процесі формування математичних понять у дітей із затримкою психічного розвитку//Дефектологія.-2000.-№ 2
2. Тарасун В. Концепція державного стандарту освіти учнів з порушеннями мовленнєвого розвитку//Дефектологія.-2000.-№ 2
3. Хохліна О. Корекційно-розвивальна робота в системі загальної освіти//Дефектологія.-2000.-№ 2