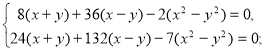Методичні рекомендації "Розв'язування текстових задач"

 

 

 

 

 

Розв’язування текстових задач

 

 

 

 

 

 

 

 

 

 

 

Виконав

Галайчук Марія Григорівна, вчитель математики

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

У посібнику розкрито етапи розв’язування текстових задач та розв’язування задач різних типів. Матеріали посібника стануть в нагоді як вчителю – молодому спеціалісту, так і досвідченому майстру освітянської ниви.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Зміст

 

 

Вступ…………………………………………………………………………….….	4
Розділ І. Задачі на спільну роботу…………………………………………….….	5
Розділ ІІ. Задачі алгебраїчного змісту…………………………………………….	19
Розділ ІІІ. Задачі фізичного змісту…………………………………………….….	29
Розділ ІV. Задачі геометричного змісту …………………………………………	38
Розділ V. Задачі з параметрами…………………………………………….……..	49
Висновки…………………………………………….……………………………..	64
Список використаних джерел…..……………………………………….……….	65

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Вступ

 

 

У чинній програмі з математики для загаль­ноосвітніх шкіл України приділяється належ­на увага формуванню вмінь школярів розв'язу­вати текстові задачі.

Розв'язування таких задач складається з етапів:

1.   Аналіз умови і того, що потрібно знайти.

Цей етап передбачає прогнозування отри­маного результату, чітке усвідомлення, що у відповіді потрібно отримати: яку величину, які одиниці вимірювання тощо.

2. Вибір невідомих.

Успішне розв'язування задачі залежить від вдалого вибору невідомих. Як правило, доціль­но вводити невідомі, що позначають шукану величну, тобто позначати через невідоме (або невідомі) те, про що запитується в задачі. Та­кож встановлюються межі значень введених невідомих.

3.   Складання рівнянь або системи рівнянь.

На цьому етапі в учнів максимально розви­вається логічне мислення, формуються навич­ки практичного застосування знань про взає­мозв'язки між величинами, подіями, процеса­ми, про які йдеться в задачі. Іншими словами, створюється математична модель задачі.

4. Розв'язування одержаного рівняння або системи рівнянь.

Під час розв'язування складеного рівняння або системи рівнянь школярі застосовують здобуті знання. Важливо не забувати про виз­начення області допустимих значень і одер­жані результати зіставити з множиною можливих значень введених невідомих і оцінки їх під час другого етапу. Якщо одержані розв'язки не задовольняють умову задачі, то їх слід відкинути.

5.    Перевірка одержаних результатів і запис відповіді.

Перевірка одержаних результатів полягає у зіставленні з прогнозом, передбаченим на пер­шому етапі. Це так звана «груба математична прикидка». Далі слід перевірити, чи викону­ються всі умови, передбачені текстом задачі. У більшості випадків перевірку можна виконувати усно. Записувати відповідь слів у порядку, у якому поставлено запитання задачі.

Р о з д і л  І

Задачі на спільну роботу

 

 

1. Два екскаватори вирили котлован за 24 дні. Перший екскаватор міг би виконати цю роботу в 1,5 раза швидше, ніж другий. За скільки днів перший екскаватор міг би вико­нати цю роботу?

Розв'язання

Приймемо всю виконану роботу за 1, а че­рез х, у позначимо кількість днів, за які мог­ли б виконати роботу, працюючи окремо, пер­ший і другий екскаватори відповідно.

Тоді продуктивність праці першого і другого екскаваторів відповідно. Виходячи з умови задачі, складаємо систему:

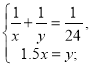
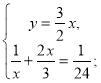
24+16-х=0,

х=40,

х≠0, у≠0

Відповідь. За 40 днів.

2. Два робітники за зміну виготовили 72 де­талі. Після того як перший робітник підвищив продуктивність праці на 15 %, а другий на 25 %, разом за зміну вони почали виготовляти 86 деталей. Скільки деталей виготовляє кожен робітник за зміну після підвищення продук­тивності праці?

Розв'язання

Нехай х деталей виготовляв за зміну пер­ший робітник, а у деталей — другий. Тоді:

х+у = 72.

Після підвищення продуктивності праці перший робітник почав виготовляти 1,15х де­талей за зміну, а другий — \,25у деталей. Тоді:

1,15х+1,25у= 86.

Маємо систему:

де х > 0 і у > 0.

Розв'яжемо систему.

 

40 • 1,15 = 46 (деталей) — виготовляє пер­ший робітник за зміну після підвищення про­дуктивності праці.

32 • 1,25 = 40 (деталей) — виготовляє другий робітник за зміну після підвищення продук­тивності праці.

Відповідь. 46 деталей, 40 деталей.

3. Дві бригади, працюючи разом, закінчи­ли ремонт ділянки шляху за 6 днів. Першій бригаді для виконання 40 % усієї роботи по­трібно було б на 2 дні більше, ніж другій бри­гаді для виконання % усієї роботи. За скільки днів могла б відремонтувати кожна з бригад окремо всю ділянку шляху?

Розв'язання

Позначимо через х кількість днів, за які відремонтує всю ділянку шляху перша брига­да, а через у — друга бригада.

Весь обсяг роботи приймемо за 1. Тоді перша бригада за один день виконає частину роботи, друга ­– , разом частину роботи. Отже,

Для виконання 40 % роботи першій бригаді потрібно (днів).

Друга бригада %=% роботи виконає  за (днів). За умовою:

Маємо систему рівнянь:

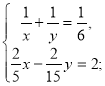
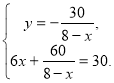
Випишемо друге рівняння системи і розв'я­жемо його:

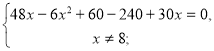
-6х²+78х-180=0,

х²-13х+30=0.

D=169-120=49,

x₁=3, x₂=10.

Тоді — не задовольняє умову задачі,

Відповідь. Кожна з бригад окремо могла б відремонтувати всю ділянку шляху за 10 і 15 днів.

4. Басейн заповнюється двома трубами за 6 год. Перша труба заповнює його на 5 год швидше, ніж друга. За який час кожна труба, діючи окремо, може заповнити басейн?

Розв'язання

Нехай перша труба заповнює басейн за х год, а друга — за у год. За умовою х+5= у.

Позначимо всю роботу (місткість басейну) через 1. Тоді перша труба за 1 год заповнить частину басейну, а друга – .

Маємо рівняння:

+=.

Складаємо систему:

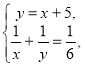
де х>0, у>0.

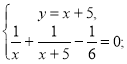
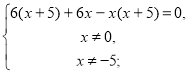
6х + 30 + 6х - x²-5х = 0,

х² - 7x - 30 = 0,

х₁ = -3 — не задовольняє умову задачі, х₂ =10, тоді у₂=15.

Відповідь. Перша труба може заповнити ба­сейн за 10 год, друга труба — за 15 год.

5. Один робітник може виконати певну ро­боту на 4 год швидше, ніж другий. Якщо вони працюватимуть разом протягом 2 год, то після цього незавершену роботу перший робітник виконає за 1 год. За який час може виконати всю роботу другий робітник, працюючи сам?

Розв'язання

Нехай другий робітник, працюючи сам, може виконати всю роботу за х год, тоді пер­ший — за (х-4) години.

Якщо прийняти всю роботу за одиницю, то — та  — продуктивність праці другого і першого робітників відповідно.

— робота, виконана першим робітником за 3 год.

— робота, виконана другим робітником за 2 год.

Складаємо рівняння:

де  x>0.

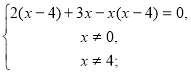
2х – 8 + 3х – х²+4х = 0,

х²  – 9х + 8 = 0.

D = 81–32 = 49,

  

Значення х не задовольняє умову задачі. Отже, другий робітник може виконати всю ро­боту за 8 год.

Відповідь. 8 год.

6. Дві бригади, працюючи одночасно, обро­били ділянку землі за 12 год. За який час об­робить цю ділянку кожна бригада окремо, якщо продуктивності праці бригад відносять­ся як 3:2?

Розв'язання

Нехай х,  у — продуктивності праці за 1 год першої і другої бригад відповідно, а вся вико­нана ними робота становить 1. Тоді, виходячи з умови задачі, складаємо систему:

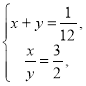
де х>0, у>0. З

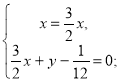
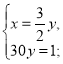
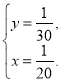
Отже, ,   — продуктивності праці першої і другої бригад за 1 год. Це означає, що бригади можуть виконати роботу, працюючи окремо, перша за 20 год, друга — за 30 год.

Відповідь. За 20 год, за 30 год.

 

7.   Два робітники, один із яких почав пра­цювати на півтора дні раніше другого, працю­ючи незалежно один від одного, виконали ро­боту за 7 днів, починаючи з моменту виходу на роботу першого робітника. Якби всю роботу доручили виконувати одному робітнику, то перший витратив би на це на 3 дні більше, ніж другий. За скільки днів кожний робітник ок­ремо виконав би всю роботу?

Розв'язання

Нехай перший робітник, працюючи сам, виконав би всю роботу за х днів, а другий— за (х-3) дні. Приймемо всю виконану роботу за 1, тоді , — продуктивність праці першого і другого робітників відповідно за 1 день.

За умовою задачі вся робота була виконана за 7 днів, але перший робітник працював усі 7 днів, а другий — 5,5 дня. Отже,               частина роботи, яку виконав перший робітник, а частина роботи, яку виконав другий робітник.

Складаємо рівняння:

де х>3,

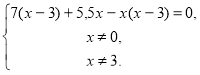
7х-21+5,5х-х²+3х= 0,

х² -15,5х+21= 0.

D = 240,25 - 84 = 156,25,

  — не задовольняє умову, що х > 3 ,

Відповідь. Перший робітник може виконати всю роботу, працюючи сам, за 14 днів, дру­гий — за 11 днів.

8.   Два робітники, працюючи разом, можуть виконати певну роботу за 12 днів. Якщо пер­ший робітник виконає половину роботи, а потім другий — ще половину, то всю роботу буде закінчено за 25 днів. На скільки днів ра­ніше один від одного робітники можуть вико­нати всю роботу, працюючи окремо?

Розв'язання

Нехай перший робітник, працюючи сам, може виконати всю роботу за х днів, а дру­гий — за у днів. Якщо вся виконана робота становить 1,то , продуктивність праці за 1 день першого і другого робітників відпо­відно, а їх спільна продуктивність. За умовою задачі робітники виконали по поло­вині роботи кожен зі своєю продуктивністю і на це витратили разом 25 днів, тому:

— дні, за які виконав перший робітник половину роботи. Аналогічно дру­гий — за 0,5у днів.

Складаємо систему:

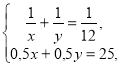
де х>0, у>0.

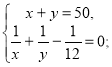
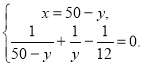
Випишемо друге рівняння системи і роз­в'яжемо його:

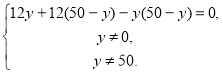
12у+600-12у-5у+у²=0,

у²-50у+600 = 0.

За теоремою Вієта:

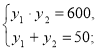
у₁=30 ,   у₂=20.

Тоді х₁ =20,  х₂ =30.

(30; 20) і (20; 30) — розв'язки системи.

Отже, працюючи окремо, робітники можуть виконати всю роботу на 10 днів раніше один від одного.

Відповідь. На 10 днів.

9. Перший насос заповнює бак на 6 год швидше, ніж другий. Обидва насоси заповню­ють бак разом за 4 год. За скільки годин запов­нить бак перший насос?

Розв'язання

 Нехай х год — час, за який заповнює бак перший насос, тоді (х+6) год — час, за якийзаповнює бак другий насос.

За умовою задачі складаємо рівняння:

у якому х>0.

4(х+6)+4х-х(х+6) = 0,

4х+24+4х-х²-6х = 0,

x² -2х-24 = 0.

D = 100,

x₁ =-4 — не задовольняє умову задачі, х₂=6.

Відповідь. Перший насос заповнює бак за 6 год.

 

10. Два крани можуть заповнити водою бак за 6 хв. Якщо перший кран заповнить 0,6 бака, а решту — другий, то бак буде заповнений во­дою за 12 хв. За скільки хвилин кожен кран, працюючи окремо, може заповнити весь бак?

Розв'язання

Нехай перший кран може заповнити бак за х хв, а другий — за у хв. Ємність бака прий­маємо за 1. Тоді — частина бака, яку заповнює перший кран за 1 хв, — частина бака, яку заповнює водою другий кран за 1 хв.

Оскільки обидва крани можуть заповнити бак за 6 хв, то маємо рівняння:

Якщо перший кран заповнить 0,6= частини бака, то він працюватиме (хв).   (хв) — час роботи другого крана.

хв. – час роботи обох кранів, що за умовою задачі дорівнює 12 хв. Складаємо друге рівняння:

Маємо систему:

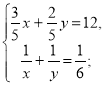
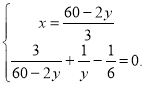
Розв'яжемо друге рівняння системи:

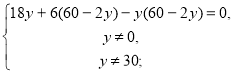
18у+360у-12у-60у+2у­²=0,

2у²-54у+360 = 0,

у²-27у+180 = 0.

D = 729-720 = 9,

  

З першого рівняння системи, підставляючи значення у₁ і у₂ одержуємо:   

(12; 12) і (10; 15) — розв'язки системи. Ос­кільки продуктивність кранів різна, то розв'я­зок системи (12; 12) не відповідає умові задачі.

Отже, перший кран може заповнити бак водою за 10 хв, а другий — за 15 хв.

Відповідь. 10 і 15 хв.

 

11. Резервуар заповнюється через два крани А і В. Заповнення резервуару тільки через кран А відбувається на 22 хв довше, ніж через кран В. Якщо ж відкрити обидва крани, то резервуар за­повниться за 1 год. За який проміжок часу кож­ний кран окремо може заповнити резервуар?

 

 

Розв'язання

Нехай х хв — проміжок часу, за який кран А заповнює резервуар, а (х-22) хв — кран В.

За умовою задачі, припустивши, що ємність резервуара дорівнює 1, складаємо рівняння:

у якому х > 22.

Після перетворень одержуємо:

х² -142х+1320 = 0.

D = 20164-5280 = 14 884,

— не відповідає умові задачі, оскільки х>22,

Таким чином, кран А може заповнити резер­вуар за 132 хв, тоді кран В —за 132-22 = 110 (хв).

Відповідь. 132 хв і 110 хв.

 

12. Для побудови будинку потрібно вийня­ти 8000 м³ ґрунту за певний час. Роботу закін­чили на 8 днів раніше, оскільки щодня пере­виконували завдання на 50 м³. За скільки днів планували закінчити роботу?

Розв'язання

Нехай х м³ грунту потрібно виймати щод­ня за планом, (х+50) м³ грунту — виймали щодня.

днів — час виконання роботи за планом.

днів — за стільки фактично виконали роботу.

Складаємо рівняння:

де х>0.

8000(х+50)-8000х-8х(х+50) = 0,

8000х+400 000 - 8000х-8х² - 400х = 0,

х²+50х-50 000 = 0,

х₁ = -250 — не задовольняє умову задачі, х₂ =200.

Отже, 200 м³ — щоденна норма за планом, тоді 8000:200=40 (днів) — час виконання ро­боти за планом.

Відповідь. 40 днів.

 

13. Бригада робітників повинна була за пев­ний час виготовити 272 деталі. Через 10 днів після початку роботи бригада почала виготов­ляти щодня понад норму 4 деталі і вже за день до строку виготовила 280 деталей. Скільки всього деталей виготовила бригада?

Розв'язання

Нехай х деталей — щоденна норма за пла­ном, тоді (х+4) деталей — бригада почала ви­готовляти через 10 днів після початку роботи.

днів — час, за який бригада мала виготовити  272 деталі.

Нехай у днів — час, протягом якого брига­да почала виготовляти щодня на 4 деталі по­над норму. За умовою задачі

Звідси

За 10 днів бригада виготовила 10х деталей. За у днів бригада виготовила (х+4)у деталей, що разом становить 280 деталей.

10х+(х+4)х = 280.

Маємо систему:

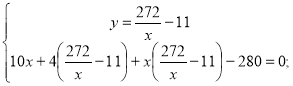
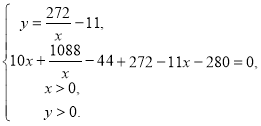
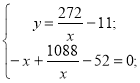
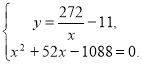
Виписуємо друге рівняння і розв'язуємо його:

х² + 52х-1088 = 0.

D = 2704 + 4352 = 7056,

— не задовольняє умову за­дачі,

(16; 6) — розв'язок системи, що задоволь­няє умову задачі.

Отже, 16 деталей — щоденна норма за пла­ном, 6 днів — час, протягом якого бригада ви­готовляла по 20 деталей. Після цього до стро­ку залишився один день. Знайдемо, скільки всього деталей виготовила бригада.

1. 1610 = 160 (деталей) — виготовили за 10 днів.
2. 20 · 6 = 120 (деталей) — виготовили за 6 днів.
3. 20 деталей виготовила бригада за день, що залишився до строку.
4. 160+120+ 20 = 300 (деталей) — всього ви­готовила бригада.

Відповідь. 300 деталей.

Р о з д і л   ІІ

Задачі алгебраїчного змісту

 

 

1. Число 180 записати у вигляді суми трьох додатних чисел так, щоб два з них відносились як 1:2, а добуток усіх трьох доданків був най­більшим.

Розв'язання

Нехай х — перший доданок. Оскільки два доданки відносяться як 1:2, то другий дода­нок можна виразити через 2х, а третій — 180-(х + 2х) = 180-3х.

Таким чином, число 180 можна записати у вигляді х+2х+(180-3х).

Складаємо добуток:

х∙2х∙(180-3х) = 360х²-6х³

Розглянемо одержаний вираз як функцію від х:

f(х) = 360х² -6х³

 і дослідимо її на найбільше значення.

f(х) =720х-18х²,

f(х)=0,

720х-18х² = 0,

18х(40-х) = 0.

Через те, що 0<х<180, то х = 40 — критич­на точка, при якій функція f(х)=360х² - 6х³ набуває найбільшого значення, оскільки при переході через цю точку похідна змінює знак з «+» на «-».

Отже, 40 — додатне число, що є першим до­данком, тоді 80 — другий доданок і 180-(40+80) = 60 – третій. Число 180 можна записати так: 180 = 40+80+60.

Відповідь. 180 = 40 + 80 + 60.

 

2. Якщо деяке двоцифрове число помножи­ти на суму його цифр, то вийде 405. Якщо по­множити число, записане тими самими циф­рами у зворотному порядку, на суму його цифр, то вийде 486. Знайти це число.

Розв'язання

Нехай (10х+у) — дане двоцифрове число, у якого х — перша цифра (число десятків), а у — друга цифра (число одиниць). Тоді (х+у) — сума його цифр. За умовою задачі складаємо перше рівняння:

(10х+у)(х+у)=405.

(10у+х) — число, записане тими самими цифрами у зворотному порядку. Складаємо друге рівняння:

(10у+х)(х+у)=486.

Маємо систему:

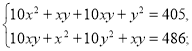
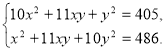
Помножимо перше рівняння системи на 6, друге — на 5:

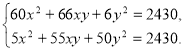
Від першого рівняння системи віднімемо друге:

55х² +l1xy-44y² =0,

5х² +ху-4у² = 0.

Одержали однорідне рівняння. Поділимо його на у²±0.

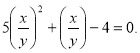
Нехай , тоді 5t² + t - 4 = 0.

D = 81,

 

Повертаючись до заміни , маємо:

або  .

Оскільки х>0 і у>0, то — не задовольняє умову задачі.

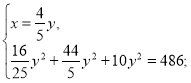
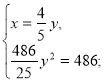
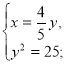
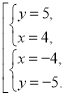
(-4; -5) — не задовольняє умову, що х> 0, у>0.

Отже, х = 4, у = 5.

Відповідь. Дане двоцифрове число дорівнює 45.

3. Якщо двоцифрове число розділити на суму його цифр, то дістанемо частку 4 і остачу 3. Якщо ж це число розділити на добуток його цифр, то дістанемо частку 3 і остачу 5. Знайти це двоцифрове число.

Розв'язання

Нехай 10х+у — дане двоцифрове число, х, у N , причому х [1; 9], у [0; 9]              (х і у - цифри).

За умовою задачі складаємо рівняння:

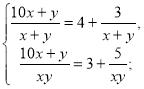
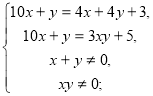
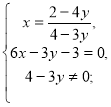
12-24у-(3у+3)(4-3у)= 0,

12-24у-12у-12+ 9у²+9у = 0,

9у² -27у = 0,

9у(у-3)= 0,

у≠0,

у=3,

Отже, (2; 3) — розв'язок системи.

Відповідь. 23.

 

4. Знайти чотири послідовні натуральні числа, якщо різниця між добутком двох більших чисел і добутком двох інших чисел до­рівнює 58.

Розв'язання

Нехай х, х+1, х+2, х+3 — чотири по­слідовні натуральні числа (х > 1).

Складаємо рівняння: (х+3)(х+2)-х(х+1) = 58,

х² +5х+6-х²-х = 58,

4х=52,

х=13.

Отже, 13, 14, 15, 16— чотири задані по­слідовні натуральні числа.

Перевірка.

15·16-13·14 = 240-182 = 58.

Відповідь. 13, 14, 15, 16.

 

5.   Знайти три послідовні парні числа, якщо різниця між добутком двох більших чисел і квадратом меншого числа дорівнює 188.

Розв'язання

Нехай 2п, 2п+2, 2п+4 — послідовні парні числа, де п >1.

Складаємо рівняння:

(2п+4)(2п+2)-(2п)² =188,

4п²+8п + 4п + 8-4п²=188,

12п = 180,

п = 15;

2п = 30,

2п + 2 = 32,

2п + 4 = 34.

Перевірка.

32·34 = 1088, 30² =900, 1088-900 = 188.

Відповідь. 30, 32, 34.

 

6.   Сума квадратів цифр двоцифрового чис­ла дорівнює 13. Якщо від цього числа відняти 9, то одержимо число, записане тими самими цифрами, але в зворотному порядку. Знайти дане число.

Розв'язання

Нехай 10х+у — дане двоцифрове число, де х і у — його цифри. За умовою задачі:

х²+у² =13.

10у+х — число, записане тими самими цифрами, але у зворотному порядку. За умовою задачі:

10х+у-9 = 10у+х.

Маємо систему:

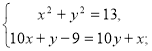
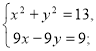
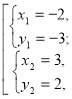
(-2; -3) і (3; 2) — розв'язки системи.

(-2; -3) — не задовольняє умову задачі.

Відповідь. 32.

 

7. Знайти чотири числа, що утворюють пропорцію, у якої сума крайніх членів дорів­нює 14, а сума середніх членів дорівнює 11. Відомо, що сума квадратів усіх чотирьох чи­сел дорівнює 221.

Розв'язання

Нехай а, b, с і d — дані чотири числа, які ут­ворюють пропорцію, тобто:

а:b = с:d,  а≠0,  b≠0,  с≠0,  d≠0.

Тоді aid— крайні члени. За умовою за­дачі

а + d = 14.

Звідси d = 14-а.

bіс — середні члени. За умовою b+с=11.

Звідси c=11-b.

Знайдемо суму квадратів усіх чотирьох чи­сел.

a² +b² +с² +d² =а² +b² + (11-b)² +(14-а)²=a²+b² +121-22b+b²+196-28a+a²=

= 2а²+2b²-28а-22b+317.

За умовою задачі ця сума дорівнює 221. Складаємо систему рівнянь:

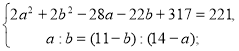
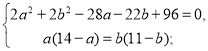
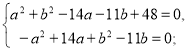
Виконаємо алгебраїчне додавання:

2b² -226 + 48 = 0,

b²-11b+24=0;

b₁=3,   b₂=8. .

Тоді

-а² + 14а+3² -11·3 = 0,

а² -14а + 24 = 0;

а₁ =2,   а₂ =12.

або:

-а² +14а + 8² -11·8 = 0,

а² -14а+ 24 = 0,

а₃ = 2,   а₄ =12.

(2; 3), (12; 3), (2; 8), (12; 8) - розв'язки системи.

d₁=14-2 = 12,

d₂= 14-12 = 2,

d₃ =14-2 = 12,

d₄=14-12 = 2,

с₁ =11-3 = 8,

с₂ = 11-3 = 8,

с₃ = 11-8 = 3,

с₄ = 11-8 = 3.

Одержали чотири варіанти послідовності запису чисел:

1) 2, 3, 8, 12;

2) 12, 3, 8, 2;

3.  2, 8, 3, 12;
4.  12, 8, 3, 2.

У кожному з чотирьох записів числа утво­рюють пропорцію, причому сума крайніх членів дорівнює 14, а сума середніх — 11.

Отже, шукані числа — це 12, 8, 3, 2.

Відповідь. 12, 8, 3, 2.

 

8. Чисельники трьох дробів пропорційні до чисел 1, 2, 5, а знаменники — відповідно до чисел 1, 3, 7. Знайти ці дроби, якщо їх середнє арифметичне дорівнює

Розв’язання

Нехай а — чисельник першого дробу, тоді 2а — чисельник другого дробу, a 5а — чисель­ник третього дробу.

b, 3b, 7b — знаменники першого, другого і третього дробів відповідно, а≠0,   b≠0.

  - дані дроби.

Знайдемо їх середнє арифметичне.

За умовою задачі воно дорівнює .

Складаємо рівняння:

Отже, перший дріб.

 

Тоді ,   другий і третій дроби.

Відповідь. ,  ,   

 

9. Найбільший спільний дільник двох додатних чисел, одне з яких становить    другого, дорівнює 27. їх найменше спільне кратне дорівнює 324. Знайти ці числа.

Розв'язання

Нехай а — одне з даних чисел, тоді — друге число. За умовою їх найбільший спільний дільник дорівнює 27, тому дані чис­ла можна розкласти на множники:

а = 27х , =27у, де х і у — невідомі множники.

Звідси випливає, що 27ху — найменше спільне кратне даних чисел, що за умовою до­рівнює 324:

27ху = 324.

Складаємо систему:

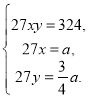
Виразимо х і у через а. Тоді система на­бирає вигляду:

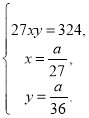
а² =36 · 324,

а = ±,

а₁ =108, а₂ =-108 — не задовольняє умову задачі.

= 81.

Перевірка.

НСД (108, 81) = 27; НСК(108, 81) - 324.

Відповідь. 108, 81.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Р о з д і л   ІІІ

Задачі фізичного змісту

 

 

1.   Один потяг за годину проходить 60 км, а другий — 40 км. Визначити відстань між дво­ма містами, якщо перший потяг проходить цю відстань на 2 год 15 хв швидше, ніж другий.

Розв'язання

Нехай s— відстань між містами. Тоді перший потяг проходить цю відстань за год, а другий за год. За умовою задачі

s=270

Відповідь. 270 км.

 

2.   Потяг повинен пройти 54 км. Пройшов­ши 14 км, він був затриманий на 10 хв біля се­мафора. Збільшивши початкову швидкість на 10 км/год, він прибув до місця призначення із запізненням на 2 хв. Визначити початкову швидкість потяга.

Розв'язання

Нехай х км/год — початкова швидкість потяга. Тоді год — час. за яким за графіком потяг повинен пройти відстань 54 км.

год —час витрачений до зупинки.

(х+10) км/год — швидкість потяга після зупинки.

год — час, витрачений після зупинки.

За умовою задачі на зупинку потяг витратив 10 хв. = год і прибув до місця призначення із запізненням на 2 хв = год.

Маємо рівняння:

де х>0.

Оскільки х>0,то 15х(х+10)≠ 0.

210х+2100+600х-810х-8100 + 2х²+20х = 0,

2x² + 20х-6000=0,

x² + 10х-3000=0,

х₁ =-60 — не задовольняє умову задачі,

х₂ =50.

Відповідь. 50 км/год.

 

3. Від пристані А одночасно вирушили за течією катер та пліт. Катер пройшов за течією 96 км, потім повернув назад і прибув у пункт А через 14 год. Знайти швидкість катера у стоячій воді та швидкість течії, якщо катер зустрів пліт на зворотному шляху на відстані 24 км від А .

Розв'язання

Нехай х км/год — швидкість течії, а у км/год — швидкість катера у стоячій воді (х>0,х>0). Тоді год — час руху плоту, год — час руху катера за течією.

год — час руху катера проти течії. За умовою задачі катер пройшов шлях за течією і по­вернувся назад у пункт А за 14 год, тобто:

До зустрічі з плотом катер витратив год, тому

Отже, маємо систему:

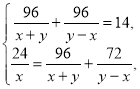
де х > 0, у > 0.

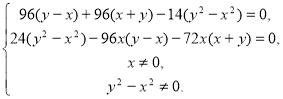
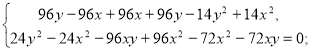
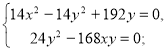
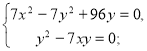
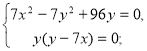
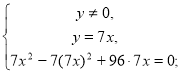
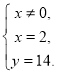
Отже, 2 км/год — швидкість течії, 14 км/год — власна швидкість катера, тобто швидкість ка­тера у стоячій воді.

Відповідь. 14 км/год, 2 км/год.

4. Студенти взяли на човновій станції на про­кат човен. Спочатку вони пропливли 20 км за те­чією річки, а потім повернулися на станцію, вит­ративши на всю прогулянку 7 год. На зворотно­му шляху на відстані 12 км від станції вони зуст­ріли пліт, який пропливав повз станцію саме в той момент, коли студенти вирушали на прогу­лянку. Визначити, з якою швидкістю рухався чо­вен за течією і яка швидкість течії.

Розв'язання

Нехай х км/год — швидкість течії, а у км/год — швидкість човна у стоячій воді.

Тоді (х+у) км/год, (у-х) км/год — швид­кість човна за течією річки і проти течії відпо­відно.

год — час руху плоту від прокатної станції до зустрічі з човном.

год — час руху човна за течією річки.

 

год — час руху човна проти течії річки.

За умовою задачі

год — час руху човна до зустрічі з плотом, що дорівнює часу руху плоту від станції до зустрічі з човном, тоді:

Складаємо систему:

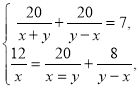
у якій х≠у, х>0 і у>0. Після спрощень одержуємо:

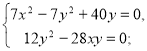
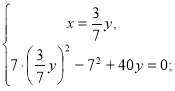
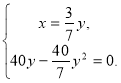
Оскільки у≠0 то:

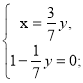
Отже, 3 км/год — швидкість течії, 7 км/год — швидкість човна у стоячій воді, 7+3-10 (км/год) — швидкість човна за течією.

Відповідь. 10 км/год, 3 км/год.

 

5. Човен долає відстань 392 км за течією річки на 14 год швидше, ніж проти течії. Швидкість течії на 14 км/год менша від влас­ної швидкості човна. Визначити швидкість течії річки.

Розв'язання

Нехай х км/год — швидкість течії річки. Тоді власна швидкість човна (х+14) км/год.

14+х+х = 14+2х (км/год) —швидкість чов­на за течією річки.

14+х-х = 14 (км/год) — швидкість човна проти течії.

392:14 = 28 (год) — час, за який човен долає відстань 392 км проти течії.

х>0,

28-14 + 2х = 0,

2х = 14,

х = 7.

Відповідь. 7 км/год.

 

6.  Катер подолав 8 км проти течії річки, по­вернув назад і пройшов за течією 36 км. Рейс тривав 2 год. Потім катер подолав 6 км проти течії річки, а за течією — 33 км, витративши на рейс 1 год 45 хв. Визначити швидкість ка­тера у стоячій воді.

Розв'язання

Нехай х км/год — швидкість катера у сто­ячій воді, а у км/год — швидкість течії річки (х>0,у>0).

(х-у) км/год — швидкість катера проти течії, а (х+у) км/год — швидкість катера за течією річки.

Складаємо систему рівнянь:

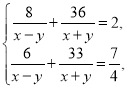
де х>0, у>0, х≠у.

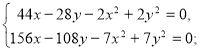
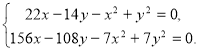
Помножимо рівняння на 7 і віднімемо від першого рівняння друге. Маємо:

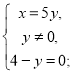
(20; 4) — розв'язок системи.

Вілмвіль. 20 км/год.

 

7. Пішохід і велосипедист вирушають одно­часно назустріч один одному з пунктів А і В , відстань між якими 40 км, і зустрічаються че­рез 2 год після початку руху. Потім вони про­довжують свій шлях, причому велосипедист прибуває в А на 7 год 30 хв раніше, ніж пішохід у В. Знайти швидкість пішохода і велосипе­диста, знаючи, що обидва весь час рухалися з незмінними швидкостями.

Розв'язання

Нехай х км/год, у км/год — швидкості пішохода і велосипедиста відповідно (х>0, у>0, у>х).

Тоді год — час руху пішохода з пункту А в В ,  год — час руху велосипедиста з пункту В в пункт А .

2х км — відстань, яку пройшов пішохід до зустрічі.

2у км — відстань, яку проїхав велосипедист до зустрічі.

Складаємо систему рівнянь:

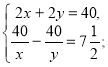
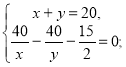
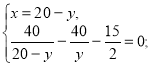
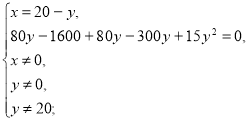
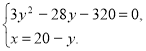
— не задовольняє умову задачі,

відповідне значення х=4.

(4; 16) — розв'язок системи, що задоволь­няє умову задачі. .

Відповідь. 4 км/год, 16 км/год.

 

8. До матеріальної точки прикладено дві сили, кут між якими дорівнює 30^о. Значення однієї з прикладених сил у раза більше, ніж значення другої, а значення рівнодійної сили на 24 Н більше, ніж значення меншої сили. Визначити значення меншої та рівно­дійної сил.

Розв'язання

Нехай х Н — значення меншої сили, тоді ()н — значення більшої сили, а

(х + 24) Н — значення рівнодійної сили, де х>0.

Відомо, що рівнодійна сила є векторною су­мою сил, прикладених до матеріальної точки.

Геометрично — це довжина діагоналі парале­лограма, побудованого на сторонах х і , причому тієї діагоналі, що виходить з верши­ни кута 30°, тобто діагональ лежить проти кута 150°. За теоремою косинусів:

(х+24)² =х²+()² -2х∙соs 150°,

x² + 48x + 576 = х² + 147х² + 14х²cos 30°,

48х+576 = 147х²+21х²,

168х² -48х-576 = 0,

7x² -2х-24 = 0 .

D= 4+672 = 676,

— не задовольняє умову задачі,

Отже, значення меншої сили дорівнює 2 Н, а рівнодійної сили 26 Н.

Відповідь. 2 Н, 26 Н.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Р о з д і л   ІV

Задачі геометричного змісту

 

 

1. Із порту одночасно вийшли два теплохо­ди, перший — на північ, другий — на схід. Че­рез 2 год відстань між ними була 60 км. Знай­ти швидкість першого теплохода, якщо вона на 6 км/год більша за швидкість другого.

Розв'язання

Нехай х км/год — швидкість першого теп­лохода (х>0), тоді (х-6) км/год — швидкість другого тепло­хода.

2х км — шлях, що пройшов перший теп­лохід за 2 год.

2(х-6) км — шлях, що пройшов другий теплохід за 2 год.

Оскільки перший теплохід рухався на північ, а другий — на схід, то напрями їх руху утворюють прямий кут. Можна скласти гео­метричну модель задачі. Це прямокутний три­кутник, у якому 2х і 2(х-6) — довжини ка­тетів, а 60 — довжина гіпотенузи. За теоремою Піфагора:

(2х)²+(2(х-6))²=60²,

4х²+4х² - 48х+144 - 3600 = 0,

8х²-48х-3456 = 0,

х² -6х-432 = 0.

D = 36 + 1728 = 1764,

— не задовольняє умову за­дачі,

Відповідь. 24 км/год.

 

2.   У прямокутному трикутнику катети відносяться як 3:2, а висота ділить гіпотенузу на відрізки, один з яких на 2 см більший від другого. Знайти довжину гіпотенузи.

 

 

Розв'язання

Нехай х см — більший із відрізків, на які висота ділить гіпотенузу, тоді (х-2) см — довжина другого відрізка.

х+х-2 = 2х-2 (см) — довжина гіпотенузи.

Якщо k — коефіцієнт пропорційності, то 3k см — довжина більшого катета.

За теоремою Піфагора:

(3k)²+(2k)²=(2х-2)²

Катет є середнім пропорційним між гіпоте­нузою та його проекцією на гіпотенузу. Про­екція катета довжиною 3k см є відрізок х см, оскільки більшому катету відповідає більша проекція. Тоді:

(3k)²=(2х-2)х.

Маємо систему:

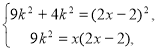
де k>0  і  k >0.

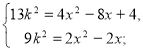
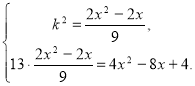
Виписуємо друге рівняння і розв'язуємо його.

13(2х²-2x)=9(4х²-8х+4),

26х² - 26х -36х² + 72х - 36 = 0,

-10х² + 46х-36 = 0,

5х² - 23х + 18 = 0.

D = 169,

, 

Оскільки через х позначено більшу частину катета, то умову задачі задовольняє значення х₂.Тоді гіпотенуза дорівнює 7,2-2= 5,2 (см).

Відповідь. 5,2 см.

3. Довжина одного з катетів прямокутного трикутника на 3 більша від довжини другого катета. Знайти довжину більшого катета, якщо площа трикутника дорівнює 9.

Розв'язання

Нехай х — довжина меншого з катетів (х>0). Тоді (х+3) — довжина другого катета.

— площа прямокут­ного трикутника.

Складаємо і розв'язуємо рівняння.

х²+3х-18=0,

х₁ = -6 — не задовольняє умову задачі, х₂ =3.

Отже, 3 — довжина меншого катета, а 6 —довжина більшого катета.

Відповідь. 6.

 

4. Периметр прямокутника дорівнює 28 см, а сума площ квадратів, побудованих на суміж­них сторонах прямокутника, дорівнює 116 см². Знайти сторони прямокутника.

Розв'язання

Нехай х см, у см — сторони прямокутни­ка, тоді його периметр дорівнює 2(х+у) см або 28 см, тобто

х+у=14

Площа першого квадрата х², а другого — у², сума цих площ х²+у², або 116 см². Складаємо систему рівнянь:

  або 

Сторони прямокутника 4 см і 10 см.

Відповідь. 4 см, 10 см.

 

5.   Периметр прямокутника дорівнює 34 см, а довжина його діагоналі 13 см. Знайти сторо­ни прямокутника.

Розв'язання

Нехай х см і у см — сторони прямокутни­ка, тоді його периметр дорівнює 2(х+у) см, або 34 см, тобто:

х+у = 17.

За теоремою Піфагора квадрат діагоналі прямокутника:

13²=х²+у²   або  х²+у²=169

Складаємо систему рівнянь та розв'язуємо її.

 

  або 

Сторони прямокутника 5 см і 12 см.

Відповідь. 5 см, 12 см.

6. Площа прямокутного трикутника дорів­нює 180 см². Знайти катети цього трикутника, якщо один із них більший за другий на 31 см.

Розв'язання

Нехай х см і у см — катети прямокутного трикутника, тоді його площа см² або

180 см², тобто

ху =360.

За умовою задачі один із катетів більший за другий на 31 см, тобто

х-у=31.

Складаємо систему рівнянь:

 

  або  — не задовольняє умову задачі.

Отже, катети прямокутного трикутника до­рівнюють 40 см і 9 см.

Відповідь. 40 см, 9 см.

 

7. Периметр прямокутного трикутника до­рівнює 48 см, а його площа 96 см². Знайти сто­рони трикутника.

Розв'язання

Нехай катети прямокутного трикутника до­рівнюють а см і b см, гіпотенуза — с см. Тоді маємо систему:

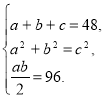
Помножимо обидві частини третього рівняння системи на 4 і додамо до другого рівняння. Одержуємо систему, рівносильну попередній:

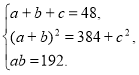
З другого рівняння

де a>0, b>0  i  c>0

,

,

=2304-96c+c²

96с = 1920,

с = 20.

Система рівнянь

рівносильна першій системі. Маємо:

  або  

Отже, катети трикутника дорівнюють 12 см і 16 см, а гіпотенуза — 20 см. Відвовідь. 12 см, 16 см, 20 см.

 

8. Гіпотенуза прямокутного трикутника більша за один з його катетів на 32 дм, а за другий на 9 дм. Знайти площу трикутника.

Розв'язання

Нехай х см і у см — катети даного прямокут­ного трикутника, тоді гіпотенузу можна вира­зити через х і через у.

х+32 = у+9,

де х > 0 і у > 0.

За теоремою Піфагора:

х²+у²=(х+32)².

Складаємо систему рівнянь:

Виписуємо друге рівняння системи і розв'я­зуємо його:

х² + х² + 46х+529 = х² + 64х+1029,

х² -18х-495 = 0,

D= 324+1980 = 2304,

— не задовольняє умову задачі,

Обчислимо площу прямокутного трикутни­ка за формулою 

дм²

Відповідь. 924 дм².

 

9.    Периметр прямокутника 60 см. Якщо довжину прямокутника збільшити на 10 см, а ширину зменшити на 6 см, то площа його зменшиться на 32 см². Знайти площу прямо­кутника.

Розв'язання

Нехай х см — ширина прямокутника, у см — довжина прямокутника, причому х>0, у>0. Тоді

2(х+у) = 60,  або  х+у=30 — периметр даного прямокутника, ху см² — площа даного прямокутника,  (у+10)(х-6) см² — площа прямокутника після зміни довжин його сторін. Складаємо систему рівнянь:

Отже, 13 см —ширина прямокутника, 17 см — його довжина, а площа дорівнює                    13 • 17 см².

Відповідь. 221 см².

 

10. Для спортмайданчика виділили ділянку прямокутної форми з діагоналлю 185 м. Вико­нуючи будівельні роботи, довжину кожної сто­рони зменшили на 4 м. При цьому прямокут­на форма була збережена, але площа виявилася меншою на 1012 м². Які розміри спортмай­данчика?

 

Розв'язання

Нехай х м, у м — початкові розміри спорт­майданчика.

Тоді за теоремою Піфагора:

х²+у²=185².

Крім цього, за умовою:

(х-4)(у-4) = ху-1012.

Маємо систему:

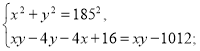
66 049 -514х+2х² -34 225 = 0,

2х²-514х+31824 = 0,

х² -257х+15912 = 0.

D = 66 049 -63 648 = 2401,

,       у₁ =257-104 = 153, у₂=257-153 = 102.

(104; 153) і (153; 104) — розв'язки системи.

Отже, початкові розміри майданчика 104 м і 153 м. Тоді остаточні розміри спортмайдан­чика: 100м × 149м.

Відповідь. 100 м, 149 м.

 

11. Ділянка прямокутної форми обгородже­на парканом. Якщо від неї відрізати по прямій деяку частину так, що залишиться квадрат, то площа ділянки зменшиться на 400 м², а дов­жина паркану зменшиться на 20 м. Визначити початкові розміри ділянки.

Розв'язання

 Нехай х м, у м — розміри ділянки, де х > 0, у>0 і х<у.

За умовою задачі складаємо систему рів­нянь.

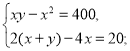
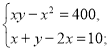
(40; 50) — розв'язок системи.

Відповідь. 40 м × 50 м .

 

12. Дано прямокутний трикутник АОВ з пря­мим кутом у точні О (0; 0). Вершини А і В лежать на осях Ох і Оу відповідно. У трикутник вписано коло радіуса R=10 см, яке дотикається до гіпотенузи у точці Р. Знайти координати то­чок А, В і Р, враховуючи, що ОА > ОВ, а пло­ща трикутника дорівнює 600 см².

Розв'язання

Нехай а і b — довжини катетів, тоді а-R+b-R=a+b-20 — довжина гіпотенузи. Очевидно, що

 (а+b-20)²=а²+b² і = 600.

Звідси а = 40 см, b= 30 см; тобто А(40; 0); B(0;30).

Знайдемо кутовий коефіцієнт прямої АВ: . Отже, рівняння прямої АВ має вигляд:

а рівняння кола:

(х-10)² +(у-10)² = 100.

Складаємо систему рівнянь:

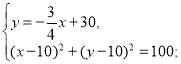
Розв'язком системи є координати точки Р.

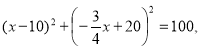
x²-32x+256=0

D = 1024-1024=0,

Отже, (16; 18) — розв'язок системи, тобто P(16; 18).

Відповідь. А (40; 0); R(0;30); P(16; 18).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Р о з д і л   V

Задачі з параметрами

 

 

1. Відстань між селищами А і В дорівнює 5 км. Із А вирушили в В одночасно по одній до­розі два автотуристи, які повинні прибути в В в один і той самий час. Але перший турист прибув до В на п год раніше, а другий — на 3n год пізніше призначеного строку, оскільки другий проїжджав за кожну годину в середньо­му на m км менше, ніж перший. Визначити се­редню швидкість кожного автотуриста.

Розв'язання

Нехай t год — запланований час руху авто­туристів.

v₁ км/год і v₂ км/год — швидкості першого і другого туристів відповідно, причому t>0,  v₁>0, v₂ >0. Тоді

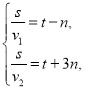
v₁-v₂=m

Віднімемо від другого рівняння перше:

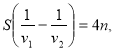
або

звідси

Зауважуємо, що розв'язками системи

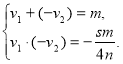
є корені квадратного рівняння

Розв'яжемо його

Отже, км/год — швидкість першого автотуриста.

км/год — швидкість другого автотуриста.

За умовою n>0 , m>0 , s>0, . Знайдені вирази для швид­костей додатні.

Відповідь. км/год,  км/год.

 

2. Швидкості пасажирського і товарного по­тягів відносяться як а:b. Пасажирський потяг вирушив від станції А на 0,5 год пізніше товар­ного, а прибув на станцію В на 0,5 год раніше від нього. Знайти швидкості пасажирського і товарного потягів, якщо відстань між А і B до­рівнює s км.

Розв'язання

Нехай х км/год — швидкість пасажирського потяга, у км/год — швидкість товарного потяга, де х>у>0. Тоді  год — час руху пасажирського потяга, год — час руху товарного потяга. За умовою задачі пасажирський потяг був у дорозі на 1 год менше, ніж товарний, тому

а їх швидкості є членами пропорції х:у=а:b.

Маємо систему:

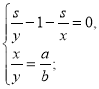
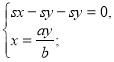
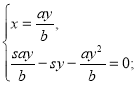
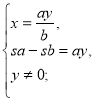
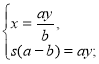
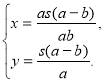
Оскільки х>у, то а>b,  s>0, а>0, b>0.

Відповідь.  км/год, км/год.

 

3. Два літаки вилетіли одночасно з пунктів А і В назустріч один одному і зустрілися на відстані а км від середини АВ. Якби перший літак вилетів на b год пізніше від другого, то вони зустрілися б на середині АВ. Якби другий літак вилетів на b год пізніше від першого, то вони зустрілися б на частині шляху від В. Знайти відстань АВ і швидкості літаків.

 

 

Розв'язання

Нехай t₁ год – час, потрібний літаку, що вилетів із А, щоб подолати відстань АВ;

t₂ год — час, потрібний другому літаку на по­долання відстані АВ у напрямі від В до А. За умовою задачі складаємо систему рівнянь.

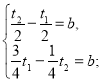
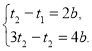
Виконаємо алгебраїчне додавання:

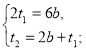
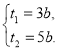
Далі складаємо рівняння:

Оскільки то

3(AB+2a)=5(AB-2a),

ЗАВ+6а = 5АВ-10а,

АВ =8а.

Далі з відношень і  знаходимо швидкості літаків.

(км/год) — швидкість першого літака,

(км/год) — швидкість другого літака, а відстань між пунктами А і В дорівнює 8а км.

Відповідь. 8а км,  км/год, км/год.

4. Міста А і В розмішені на прямолінійній трасі на відстані 5 одне від одного. Із А в В од­ночасно вийшли два пішоходи, а із В в А в той самий час виїхав велосипедист. Проїхавши k-ту частину шляху від В до А (0 < k < 1), вело­сипедист зустрів першого пішохода, а потім, проїхавши всього шляху, зустрів другого пішохода. На якій відстані від місця зустрічі другого пішохода і велосипедиста у момент їх зустрічі знаходився перший пішохід? Швид­кості пішоходів і велосипедиста сталі.

Розв'язання

Нехай v₁, км/год, v₂ км/год — швидкості першого і другого пішоходів відповідно,

v₃ км/год — швидкість велосипедиста, v₁ > 0, v₂>0, v₃>0.

t₁ год — момент часу від початку руху до зустрічі першого пішохода і велосипедиста;

t₂ год — момент часу від початку руху до зустрічі другого пішохода і велосипедиста. Маємо систему рівнянь:

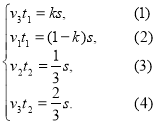
Із (1) і (2) рівнянь знаходимо, що

з рівняння (4):

Нехай х км — шукана відстань, тоді

Оскільки пішоходи йдуть до пункту В, то одержаний результат матиме зміст, якщо , тобто, якщо виконується нерівність .

Ця нерівність справедлива, якщо

Якщо відстань між пішоходами в момент часу t₂  дорівнює , оскільки до цьо­го часу перший пішохід дійде до кінцевого пункту.

Якщо то умова задачі не виконується (велосипедист раніше зустріне другого пішохода).

Отже, перший пішохід був на відстані км, якщо , якщо від зустрічі велосипедиста другого пішохода.

Відповідь. , якщо , якщо

 

5. Два велосипедисти виїхали одночасно з пункту А, їдуть з різними, але сталими швид­костями до пункту В, приїхавши, відразу повер­таються назад. Перший велосипедист, обігнав­ши другого, зустрічає його на зворотному шля­ху на відстані а км від В. Потім, прибувши в А, знову повертається до В, зустрічаючи на шляху другого велосипедиста, пройшовши k-ту час­тину відстані А до В. Знайти відстань від А до В.

Розв’язання

До першої зустрічі перший велосипедист проїхав (s+a) км, другий — (s-а) км, де s км — відстань від А до В. До другої зустрічі вони проїхала відповідно км і км.

Якщо два матеріальні тіла рухаються зі ста­лими швидкостями, то відношення швидкос­тей тіл при рівності витраченого часу дорівнює відношенню пройдених тілами шляхів. Тому для знаходження s маємо рівняння:

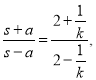
звідси s=2ak км, де а>0, k>0.

Відповідь. 2аk км.

 

6. Із пунктів А і В назустріч один одному одночасно вирушили пішохід і велосипедист. Після зустрічі пішохід продовжив свій рух до пункту В_, а велосипедист повернувся назад і також поїхав до пункту В. Пішохід прийшов у пункт В на t год пізніше велосипедиста. Скільки часу минуло до зустрічі, якщо швидкість пішохода у k разів менша від швид­кості велосипедиста?

Розв'язання

Нехай до зустрічі минуло х год. Одну і ту саму відстань від місця зустрічі до пункту В ве­лосипедист подолав за х год, а пішохід за (x+t) год. Оскільки при одній відстані час обернено пропорційний до швидкості, то

де х>0 , t>0.

, де к>1.

Відповідь. .

 

7.   Для випробування мотоциклів різних мо­делей два мотоциклісти виїхали одночасно від В до А. Кожний їхав з незмінною швидкістю і, приїхавши до кінцевого пункту, відразу повер­нули назад. Першого разу вони зустрілися на відстані g км від В, другого разу — на відстані g км від А через t год після першої зустрічі. Знайти відстань між А і В і швидкості обох мо­тоциклів.

Розв'язання

Нехай х — відстань між пунктами А і В, де x>0, v₁, v₂ – швидкості мотоциклів v₁>0, v₂>0.

За час t перший мотоцикліст проїхав відстань, що дорівнює p+x-g , а другий g+х-р.

Складаємо систему рівнянь:

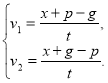
З іншого боку, відношення швидкостей до­рівнює відношенню відстаней, пройдених до першої зустрічі, тобто:

Підставивши у це рівняння значення v₁ і v₂ із системи, одержуємо рівняння, з якого зна­ходимо x.

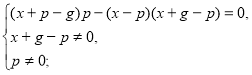
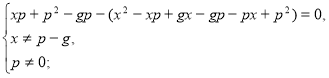
Тоді , 

Отже, відстань між А і B дорівнює 3p-g, а швидкості мотоциклів i .

Відповідь. (3p-g) км,  км/год, км/год.

 

8. Літак вилетів від А до В по прямій. Че­рез деякий час внаслідок зустрічного вітру він зменшив швидкість до v км/год, тому запіз­нився на t₁, хв. Під час другого рейсу літак з тієї самої причини зменшив свою швидкість до тієї самої величини, але на d км далі від А, ніж пер­шого разу, і запізнився на t₂ хв. Знайти по­чаткову швидкість літака.

Розв'язання

 Нехай х км/год — початкова швидкість літака. Різниця між часом спізнення літака у першому і другому рейсах дорівнює год і пов'язана з тим, що шлях довжиною d км був пройдений з різними швидкостями: під час першого рейсу швидкість була v км/год, під час другого — х км/год (на решті шляху швид­кості були однаковими).

Одержуємо рівняння:

.

Розв'яжемо це рівняння відносно х:

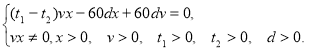
х((t₁-t₂)v-60d)=-60dv,

Оскільки значення всіх параметрів додатні, то t₂ > t₁.

Відповідь. км/год.

 

9. По колу у протилежних напрямах рухаються два тіла: перше рівномірно з лінійною швидкістю v, а друге — рівноприскорено з лінійною швидкістю а. У початковий момент часу обидва тіла були в точці А і швидкість дру­гого дорівнювала нулю. Через скільки часу відбудеться перша зустріч цих тіл, якщо друга зустріч буде знову у точці А?

Розв'язання

Позначимо через t час, що минув до пер­шої зустрічі, через t' — час, що минув до дру­гої зустрічі, і через R — радіус кола. За час t перше тіло пройшло шлях vt, а друге —

Сума цих відстаней дорівнює довжині кола:

За час t' кожне тіло пройшло однакову відстань, що дорівнює довжині кола:

Виключаючи звідси t', знаходимо

Підставивши це значення R у перше рівняння, одержуємо квадратне рівняння відносно t.

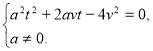
Оскільки v>0 , а > 0, то t₁ <0, тому t₁ не задовольняє умову задачі.

Отже, — час, через який відбу­деться перша зустріч.

Відповідь. .

 

10. По колу радіуса R рівномірно в одно­му напрані рухаються дві точки. Одна з них робить повний оберт на t c швидше від дру­гої. Час між двома послідовними зустрічами точок дорівнює Т. Визначити швидкості цих точок.

Розв’язання

Нехай х м/с,  у м/с — швидкості точок, причому х>у,  х>0,  у>0.

Складаємо перше рівняння:

За умовою задачі час Т точка, що ру­хається з більшою швидкістю, пройде по колу відстань на більшу, ніж друга точка. Ви­ходячи з цього, складаємо друге рівняння:

Тх-Ту=.

Маємо систему:

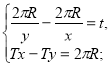
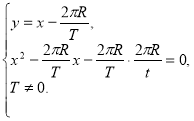
Виписуємо друге рівняння системи і розв'я­зуємо його:

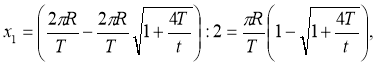
оскільки > 1, то х₁<0 — не задоволь­няє умову задачі.

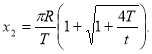
Знайдемо значення у, що відповідає зна­ченню х₂:

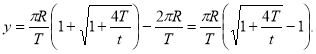
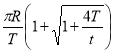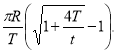Відповідь. м/с, м/с.

 

11. Троє мандрівників А, В і С переправляли­ся через водосховище шириною s км: А — плив зі швидкістю v км/год, а В і С— використали моторний човен, швидкість якого v₁ км/год. Че­рез деякий час після початку переправи С вирі­шив решту шляху пливти самостійно з тією са­мою швидкістю, що і А, В тим часом повернув назад, щоб узяти з собою А. А сів у човен і про­довжив шлях разом з В. До протилежного бе­рега всі троє припливли одночасно. Визначи­ти, скільки часу тривала переправа.

Розв'язання

Нехай х — відстань від першого берега до того місця, де С залишив човен. Зауважимо, що на цій самій відстані від другого берега А сів у човен. Способи, якими подолали пере­праву A i С, відрізняються лише тим, що С спочатку плив на човні, а потім самостійно, а А — навпаки. Оскільки вони пливли з рівни­ми швидкостями v, причому v≠v₁, і витрати­ли один і той самий час на переправу, то за­значені відстані повинні бути рівними. Тому можна скласти рівняння, позначивши через s відстань від місця, де С залишив човен, до дру­гого берега.

У цьому рівнянні ліва частина виражає час, витрачений човном на подолання відстані до зустрічі з А , а права частина — час, що витра­тив А до зустрічі з човном.

Розв'яжемо рівняння відносно х:

(x+s-2s+2x)v-(s-x)v₁=0

де x, s, v, v₁ —додатні величини.

відстань від початку переправи до місця, де С залишив човен.

Нехай Т — час, протягом якого тривала пе­реправа, тоді

Підставивши значення у цей вираз, одержуємо:

Відповідь.  год.

 

12. Відстань між двома містами дорівнює а км. З цих міст назустріч один одному виїха­ли два автомобілі і зустрілися через 2t год. Якби перший автомобіль виїхав на t год рані­ше, ніж другий, то вони зустрілися б на сере­дині шляху. Визначити швидкість кожного ав­томобіля.

Розв'язання

Нехай швидкість першого автомобіля х км/год, а другого у км/год (х>0,у>0).

Тоді перший проїде половину шляху за год, а другий — за год. 

За умовою задачі

Якщо автомобілі виїжджають одночасно, то весь шлях вони проїдуть за год.

Складаємо систему рівнянь:

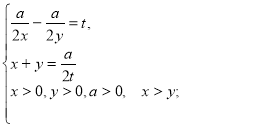
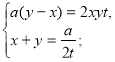
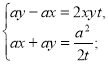
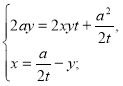
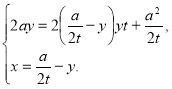
Виписуємо перше рівняння системи і роз­в'язуємо його.

— не задовольняє умову,

Знайдемо відповідне значення х:

Причому   що відповідає умові

Відповідь.  км/год,  км/год.

 

13. Два автомобілі виїжджають одночасно з пункту А до пункту В, відстань між якими дорівнює р км. Швидкість одного автомобіля на m км/год більша за швидкість другого, тому він приїжджає до В на h год раніше. Визна­чити швидкості автомобілів.

Розв'язання

Нехай швидкість першого автомобіля х км/год, тоді швидкість другого автомобіля (х + m) км/год.

Перший автомобіль проїжджає р км за — год, а другий за год.

Складаємо рівняння:

де x>0,  t>0,  m>0,  p>5.

p(x+m)-px-tx(x+m)=0,

px+mp-px-tx²-tmx=0,

-tx²-tmx+pm=0,

x²+mx-=0.

— не задовольняє умову задачі.

— швидкість першого автомобіля, а швидкість                         другого .

Відповідь.  км/год, км/год.

 

 

 

 

В и с н о в к и

 

 

Звичайно, така систематика умовна, оскіль­ки, наприклад, задачі фізичного змісту можна класифікувати здебільшого як задачі «на рух», а задачі алгебраїчного змісту як задачі на залежність між компонентами арифметичних дій». На практиці часто зустрічаються задачі змішаних типів.

Матеріал статті допоможе старшокласникам у підготовці до незалежного зовнішнього оці­нювання з математики.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Список використаних джерел

 

 

1. Горделадзе. Ш.Г., Кухарчук М.М. Збірник конкурсних задач з математики – Вища школа, 1990.
2. Дыбов П.Т., Забоев А.И. Сборник задач по математике для поступающих в вузы. Учебное пособие – Высшая школа, 1989.
3. Крамор В.С. Повторяем и систематизируем школьный курс алгебры и начал анализа. Просвещение, 1990.
4. Колесникова Л.В., Коротіна Г.Й. Алгебра. Дидактичні матеріали. 9 клас: Навчальний посібник. – Х.: Світ дитинства, 2001.
5. Сєров М.І., Самоздран А.О. Посібник з елементарної математики –  Полтава, 2005.