Методичні вказівки для виконання практичного заняття по темі «Деформація згину»

Методичні вказівки

для виконання практичного заняття

по темі «Деформація згину»

Для студентів спеціальності

208 «Агроінженерія» ІІ курсу денної форми навчання

Викладач:  Лоїк О.А.

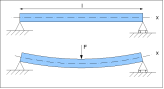
Деформа́ція зги́ну або згин — тип деформації бруса (балки), що полягає у викривленні осі прямого бруса чи зміні кривини осі кривого бруса в результаті виникнення згинальних моментів у його перерізах від прикладених навантажень (поперечних сил і/або згинальних моментів у площині, що проходить через вісь бруса).

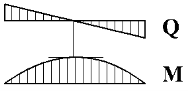
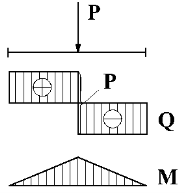
Локальна деформація різних частин тіла при згинанні різна. Наприклад, у випадку, зображеному на рисунку, верхня частина балки стискається, а нижня — розтягується.

 

 

 

 

Види згину

Стосовно до бруса розрізняють згин плоский, або простий, та складний. При плоскому (простому) згині зовнішні сили діють в одній з головних площин бруса (вони проходять через вісь бруса і головні осі інерції поперечного перерізу, див. Моменти інерції плоских перерізів, при складному згині — в різних площинах. Різновидом складного є косий згин, коли навантаження діють у площині, що не збігається з будь-якою з головних площин.

Залежно від сил, що діють у поперечному перерізі бруса, згин буває чистим (при наявності лише згинальних моментів), поперечним (діють поперечні сили), поздовжнім (випинання під впливом стискувальних сил, спрямованих вздовж осі) і поперечно-поздовжнім.

Поперечна сила в перерізі балки чисельно дорівнює алгеб­раїчній сумі всіх зовнішніх сил, які діють справа або зліва від перерізу.

Прави­ло знаків. Зовнішні сили, які намагаються повернути відрізану частину балки, відносно перерізу, за ходом часової стрілки визивають додатну поперечну силу, і навпаки проти ходу часової стрілки від’ємну .

 

 

         

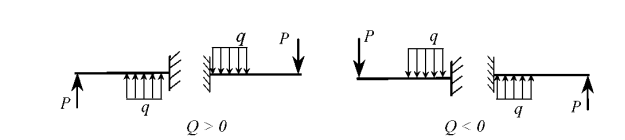
Згинальний момент у перерізі балки чисельно дорівнює алгебраїчній сумі моментів відносно центра ваги перерізу всіх зовнішніх сил, які діють справа або зліва від перерізу.

Правило знаків. Якщо зовнішнє навантаження намагається зігнути балку опуклістю донизу, то згинальний момент у перерізі вважають додатним, і навпаки.

 

 

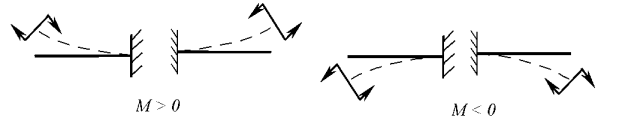
Побудова епюр попереч­них сил та згинальних моментів

 

Під час побудови епюр поперечних сил і згинальних моментів рекомендується дотримуватися такої послідовності:

1) Визначити реакції опор (для консолі їх можна не знаходити).

2) Розбити брус на ділянки, границями яких є перетини, в яких прикладені зосереджені сили і пари або розпочинається чи закінчується розподільне навантаження. Такі перетини називають характерними.

3) Користуючись методом перетинів, будуємо епюру поперечних сил. Якщо поперечна сила, змінюючись безперервно, проходить через нульове значення, то необхідно визначити абсцису перерізу, де Q стає нульовим.

4) Визначити в характерних перетинах значення згинальних моментів і за знайденими ординатами побудувати епюру М_х.

 

 

Взаємозв’язок між видами епюр і навантаженням

 

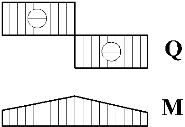
	На ділянках, де , епюра Q паралельна осі X, епюра М – прямолінійна, нахилена.
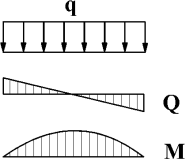
	На ділянках, де , епюра Q прямолінійна нахилена, епюра М – параболічна з випуклістю назустріч q.
	На ділянках, де , М – зростає, де , М – убуває.
	В перерізах, де , дотична до епюри М паралельна осі Х (на епюрі М - екстремум).
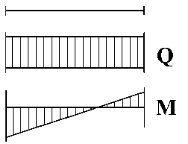
	В перерізах, де прикладена зосереджена сила Р, на епюрі Q стрибок на величину і в напрямку сили ,  на епюрі М – перелом, вістря якого направлене назустріч Р.
	В перерізах, де прикладений зосереджений момент М, на епюрі М стрибок на величину М, на епюрі Q змін немає.

 

 

Приклад розв’язку для самостійної та індивідуальної роботи. Розрахунок балок на міцність при плоскому згині.

 

Приклад:Для балки при α = 0 побудувати епюри згинальних моментів та поперечних сил і на підставі епюри згинальних моментів М підібрати стальну балку прямокутного поперечного профілю (h=2b) при []=160 МН/м² .

 

 

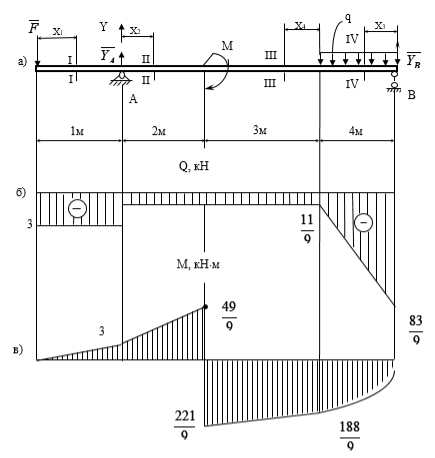
Розв’язання

Розглянемо просту балку на двох опорах (рис. а): опора А – нерухомий шарнір; опора В – рухомий шарнір. Дію в’язей (шарнірів) на балку замінюємо реакціями в’язей   які знаходимо з рівнянь рівноваги при F=3кН, q=2кН/м, М=30кНм

,.

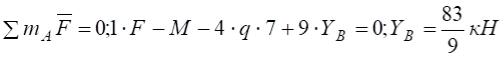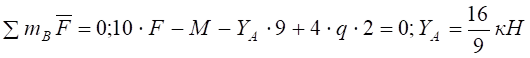Перевірка:

,

.

 

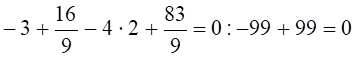Балка має чотири ділянки, тому проводимо чотири довільні перерізи (рис.а) і знаходимо поперечну силу Q_і та згинальний момент М_і у кожному перерізі.

Переріз -:      

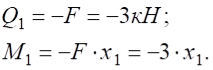
при 

при .

 

Переріз - :   

при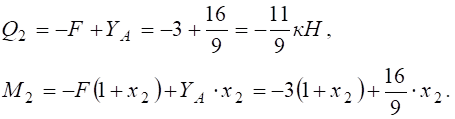 

при .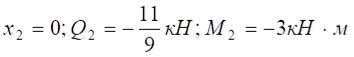

 .

 

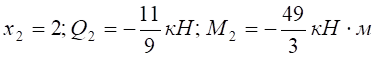Переріз -:           

при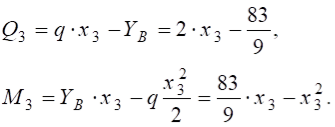  

при .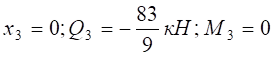

 .

 

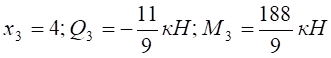Переріз V-V:         

 

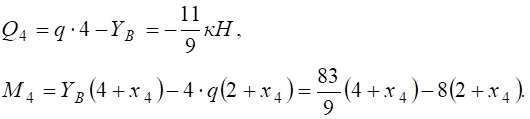
при 

.

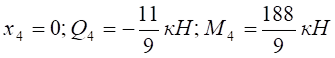при

 .

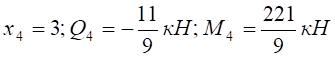За отриманими даними Q_і та М_і  (і=1,2,3,4) будуємо епюри Q (рис. б) та М (рис. в).

Ординати Q_і та М_і відкладаємо перпендикулярно до осі балки. Для поперечної сили Q_і додатні значення відкладаємо над базовою лінією (відносно балки), а епюру М_і будуємо на розтягнутих волокнах.

Розміри поперечного перерізу балки будемо знаходити із умови міцності

,

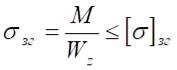Де   – момент опору.

Так як за умовою h=2b, то    .

Знайдемо мінімальне значення ширини b поперечного профілю балки:

 

 

,

 

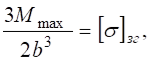
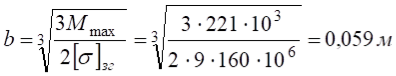де  – максимальне значення згинального моменту (рис. в).

 

Відповідь: приймаємо b=60мм, h=120мм.

 

Приклад 2.

Побудувати епюри Q і М для вільно лежить балки прольотом ℓ, навантаженої зосередженою силою F.

Рішення.
У двухопорной балці нерухомий шарнір накладає два обмеження на переміщення балки; в горизонтальному і вертикальному напрямку. Тому, в загальному випадку в шарнірно-нерухомій опорі виникають дві реакції: горизонтальна R_Аz  і вертикальна R_АУ.

Так як при поперечному вигині весняні сили прикладені перпендикулярно осі балки, то вони не викликають переміщення балки в горизонтальному напрямку, тому, складова R_AZ = 0 і надалі її не зображують на малюнку. У рухомій шарнірної опорі виникає одна вертикальна реакція R_В перпендикулярна опорної площини. Звільнивши балку від опор, замінивши їх дію на балку реакціями R_А і R_В, отримаємо розрахункову схему, показану на .
При визначенні реакцій двохопорних балок в опорі матеріалів прийнято записувати рівняння рівноваги в такій формі:

1. Сума проекцій всіх сил на вісь балки (вісь Z) дорівнює нулю
   
   F_iZ =0, ∑R _АZ =0,

2. Сума моментів всіх сил відносно опори А дорівнює нулю:

∑М_А (F_i)=-Fa+R_Вℓ = 0,

3. Сума моментів всіх сил відносно опори В дорівнює нулю:

∑М_В(F_i) =-Fℓ  R_Аℓ = 0.

Визначаємо з другого рівняння реакцію  ;

З третього

Після визначення реакцій обов'язково перевірка. Для цього використовується рівняння - сума проекцій всіх сил на вертикальну вісь у дорівнює нулю.

Перевірка:

 

 

тобто опорні реакції визначені правильно.

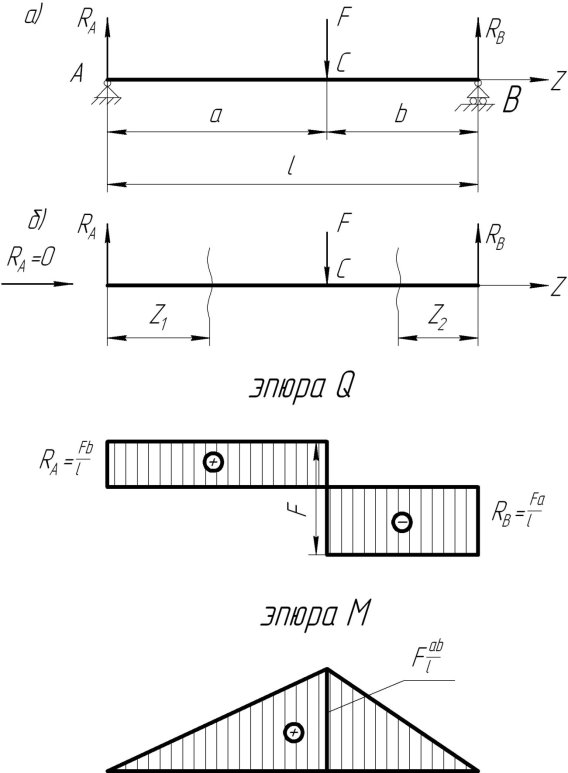
Побудова епюри Q. Знаючи реакції, можна скласти аналітичні вирази для будь-якого перетину балки. Розбиваємо балку на дві ділянки, межами яких є перетин, в якому прикладена зосереджена сила F.

Проводимо переріз на відстані Z₁ від лівої опори і відкидаємо праву частину балки. На ліву частину балки діє одна сила R_А, яка зрушує ліву частину балки вгору, причому вона залишається постійною протягом всієї ділянки від опори А (Z₁ = 0) до перетину С (Z₁ = а), де прикладена сила F, так як в рівнянні      відсутня змінна Z _1.

Отже, на даній ділянці епюра Q обмежена прямою паралельної осі балки.
Перетин II-II на ділянці СВ проводимо на відстані Z₂ від правої опори. Праворуч від перетину діє реакція R_B, яка прагне зрушити балку вгору і згідно з правилом знаків для Q поперечна сила в цьому перерізі має знак мінус і дорівнює        

Значення поперечної сили на цій ділянці також є постійною протягом всієї ділянки від перетину В (Z₂ = 0) до перетину С (Z₂ = в), т.е і на цій ділянці епюра Q обмежена прямою, паралельною осі Z.

Побудова епюри М. Аналітичні вирази згинального моменту на ділянці АС визначаємо, розглядаючи ліву частину балки, на яку діє реакція R_А, вона згинає ліву частину балки опуклістю вниз

 

При Z₁ = 0, 

тобто на опорі А згинальний момент дорівнює нулю.

При Z₁ = а

 

тобто згинальний момент зростає прямо пропорційно збільшенню відстані Z_1, досягаючи найбільшого значення в перетині С. Таким чином, на ділянці АС епюра М обмежена похилій прямій, так як рівняння М_I - рівняння прямої лінії.

Ділянка СВ. Розглянемо перетин II-II на відстані Z₂ від правої опори. Закріпимо мисленнo балку в перетині II-II і докладемо до правої частини балки реакцію R_B, вона буде згинати відсічену частину балки опуклістю вниз і величина згинального моменту в перерізі II-II буде дорівнює:

 

 

При Z₂ = 0, 

При Z₂ = b

 

За знайденими ординатам будуємо епюру згинальних моментів.
Небезпечним перетином буде перетин С, в якому згинальний момент досягає максимального значення.

Література

1.Опір матеріалів. Підручник /Г. С. Писаренко, О. Л. Квітка, Е. С. Уманський. За ред. Г. С. Писаренка — К.: Вища школа,1993. — 655 с. 

 2.Опір матеріалів: Навч. посіб. для студентів ВНЗ. Рекомендовано МОН / Шваб'юк В. І. — К., 2009. — 380 с.

3.Мильніков О. В.  Опір матеріалів. Конспект лекцій / Олександр Володимирович Мильніков. — Тернопіль: Видавництво ТНТУ, 2010. — 257 с.