Методичні вказівки "Геометричні тіла та поверхні"

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

ВІДОКРЕМЛЕНИЙ СТРУКТУРНИЙ ПІДРОЗДІЛ

«ПОЛТАВСЬКИЙ ФАХОВИЙ КОЛЕДЖ

НАЦІОНАЛЬНОГО УНІВЕРСИТЕТУ ХАРЧОВИХ ТЕХНОЛОГІЙ»

 

 

 

 

 

 

 

 

 

Геометричні тіла та поверхні.

методичні вказівки

до вивчення дисципліни

«Математика»

для студентів всіх спеціальностей

 

 

 

 

 

 

 

 

 

 

 

Полтава

2020

Геометричні тіла та поверхні: методичні вказівки до вивчення
дисципліни «Математика» для студентів всіх спеціальностей.

 

Укладач: Хименко Л.О. – Полтава: ВСП ПФК НУХТ, 2020. – 58 с.

 

 

 

 

СХВАЛЕНО

на засіданні предметної комісії загальноосвітніх дисциплін

 

 

 

Зміст

Зміст

Вступ.

Геометричне тіло.

Контрольні запитання.

Основні види геометричних тіл.

Многогранники.

Контрольні запитання.

Правильні многогранники.

Тетраедр.

Октаедр.

Куб.

Додекаедр.

Ікосаедр.

Контрольні запитання.

Призма.

Паралелепіпед‎.

Контрольні запитання.

Піраміда.

Контрольні запитання.

Тіла обертання

Циліндр.

Перерізи циліндра.

Контрольні запитання.

Конус.

Перерізи конуса.

Контрольні запитання.

Куля. Сфера.

Контрольні запитання.

Приклади розв’язування типових задач.

Список використаних джерел.

 

Вступ.

Зрозуміло, що геометрія потрібна не тільки для того, щоб називати частини побудов або форми предметів, які нас оточують. За допомогою геометрії можна знаходити їх об'єми, площі, а також відстань до точок, до яких не можливо дістатись.

Вчений Фалес знайшов відстань від корабля до берега та висоту піраміди. У Єгипті завжди сіяє сонце, тому добре вимірюється висота піраміди. А як бути, якщо дерево у лісі, а на небі хмари? Як знайти відстань між двома пунктами, якщо між ними є болото? Як визначити положення корабля в морі? На всі ці запитання можна отримати відповідь за допомогою геометрії.

 І все-таки, геометрія, що стояла біля колиски людського розуму, може допомогти сьогодні людині зробити ще один стрибок у своєму розвитку: інтелектуальному, духовному і моральному. Треба не втратити цю можливість. Може в цьому і полягає відповідь на запитання: «Навіщо вчити геометрію».

Не тільки для того, щоб не прорахуватися з покупкою рулонів шпалер! Крім  практичної користі, в геометрії є особливий сенс. Логічне мислення – один із шляхів до незалежності особистості.

Багато геометричних фігур зустрічаємо ми навколо себе. Складну форму мають деталі машин – гайки, вінти, колеса й інші. Поверхню таких предметів можна вивчати геометричними методами, тому геометрія необхідна робочим багатьох спеціальностей, які мають справу з обробкою дерева та металу.

За допомогою геометрії математики познають оточуючий їх світ, отримують потрібність будувати більш складні машини, розробляти плани розвитку народного господарства. Без відкриттів математиків не змогли б злетіти ракети, не працювали б атомні електростанції, не з’явився б оточуючий нас світ техніки. [15]

Навколишнє середовище дуже різноманітне. Фізичні тіла, які нас оточують,  можуть мати дуже складну форму, і вивчення всього різноманіття таких форм неможливе. Розглянимо будову основних видів тіл, які частіше використовуються в діяльності людини, вивчимо основні їх властивості. Це дасть можливість досліджувати фізичні тіла, вважаючи їх складеними з найпростіших.

 

Геометричне тіло.

 У стереометрії вивчають фігури у просторі, які називаються геометричними тілами. Із усього різноманіття просторових фігур виділимо ті, які найповніше відображають будову реальних тіл.

Поняття геометричного тіла необхідно для описання форми і будови реальних фізичних тіл. Фізичне тіло можна уявити суцільним, і тоді у нього виділяється внутрішня частина і межа (поверхня), що відокремлює внутрішню частину від навколишнього світу. [1]

Математичною моделлю фізичного тіла, тобто геометричним тілом, вважають таку фігуру в просторі, яка має таку саму будову, як і фізичне тіло.

Точка фігури називається внутрішньою, якщо всі точки простору, що розміщені достатньо близько до даної точки, належать фігурі. [1]

Геометричне тіло — зв'язна частина простору, обмежена замкнутою поверхнею своєї зовнішньої границі. Геометричним тілом називають так само компактну множину точок і дві точки з цієї множини можна з'єднати відрізком, який цілком буде проходити в межах тіла, що вказує на склад геометричного тіла з множини внутрішніх точок. [10]

Так, наприклад, всі точки паралелепіпеда (Рис.1), які не лежать на його гранях, є внутрішніми.

Точка називається граничною точкою даного геометричного тіла, якщо серед як завгодно близьких до неї точок (включаючи її саму) є точки, які належать тілу, так і не належать йому.

 

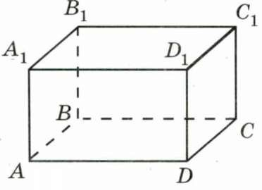
Рис.1

Множина всіх граничних точок тіла називається його границею. На основі цього будується уявлення геометричного тіла як частини простору, відокремленої від решти простору поверхнею — границею цього тіла. Так,  наприклад,  границею кулі є сфера ( Рис.2), а  границя циліндра складається з  двох  кругів — основ  циліндра  і  бічної  циліндричної поверхні  ( Рис.3).

Рис.2

Геометричне тіло за визначенням у «Началах» Евкліда (Книга XI) — частина простору, що має довжину, ширину і глибину і обмежена поверхнею. [10]

Фігура у просторі називається обмеженою, якщо відстань від даної точки до всіх точок фігури менша за деяке число. [1]

Межею фігури називається сукупність її граничних точок. Межа тіла називається його поверхнею. [1]

 

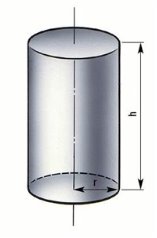
Рис.3

Так, наприклад, поверхнею кулі є сфера, поверхню паралелепіпеда складає шість прямокутників.

Рис.4

Приклади геометричних тіл ( Рис.4): 1-куля, 2-тетраедр, 3-куб, 4-тор, 5-порожнистий циліндр, 6-круговий циліндр, 7-конус, і 8-вузол.

Геометричне тіло — уявне тіло, в якому зберігаються лише форма і розміри при повному абстрагуванні від усіх інших властивостей. На відміну від реальних предметів геометричні тіла, як і всякі геометричні фігури, є уявними об'єктами.

Оскільки в геометрії розглядаються тільки геометричні тіла, то їх прийнято називати просто тілами.

Фігури, які зображені на Рис.5 не є геометричними тілами.

Рис.5

Всі геометричні фігури можна класифікувати таким чином:

При вивченні властивостей геометричних тіл — уявних об'єктів, формуються уявлення про геометричні властивості реальних предметів (їх форму, взаємне розташування і т.д.) які можна використати в практичній діяльності.

 

Контрольні запитання.

1. Які точки називаються внутрішніми?
2. Які точки є внутрішніми для: а) кулі; б) куба; в) сфери?
3. Які точки називаються граничними?
4. Які точки є граничними для: а) кулі; б) куба?
5. Чи може не належати фігурі її: а) гранична точка; б) внутрішня точка?
6. Чи є фігура тілом, якщо в неї вилучити точку?
7. Чи завжди перетин тіла є тілом?
8. Чи завжди об’єднання тіл є тілом?

 

Основні види геометричних тіл.

Розглянимо найважливіші види геометричних тіл, які широко застосовуються у науці, техніки, побуті.

Всі геометричні тіла діляться на многогранники і тіла обертання.

Класифікація геометричних тіл:

Многогранники.

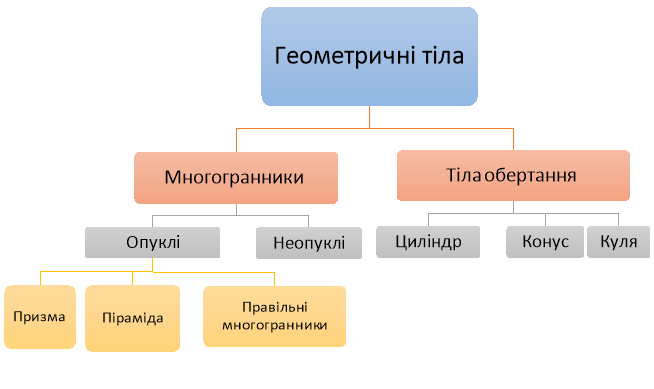
Многогранник — це таке тіло, поверхня якого складається із скінченної кількості плоских многокутників.(Рис.6)

Многогранник називається опуклим, якщо він лежить по один бік від площини кожного з плоских многокутників на його поверхні. Спільна частина такої площини і поверхні опуклого многогранника називається гранню. Грані опуклого многогранника є плоскими опуклими многокутниками.

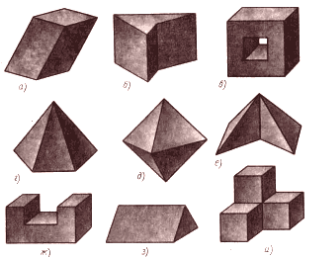
Рис.6

Сторони граней називаються ребрами многогранника, а вершини — вершинами
многогранника. [11]

Відрізок, який сполучає дві вершини, що не належать одній грані,- діагональ многогранника.

На рис.7 зображено опуклі многогранники.

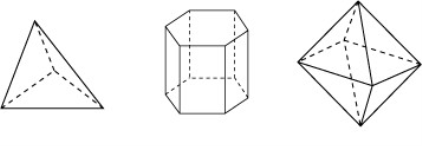
Рис.7

На рис.8 зображено неопуклі многогранники.

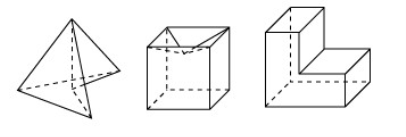
Рис.8

На рис.9 зображено елементи многогранника.

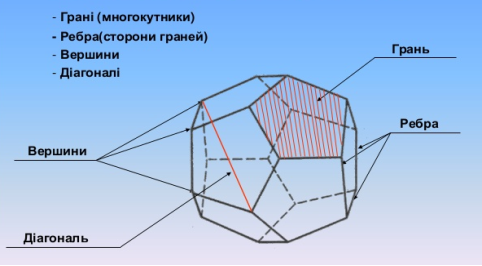
Рис.9

Пояснимо сказане на прикладі відомого вам куба (Рис. 10). Куб — це опуклий многогранник. Його поверхня складається з шести квадратів АВСD, ВЕFС, ... . Вони є його гранями. Ребрами куба є сторони цих квадратів АВ, ВС, ВЕ, ... .Вершинами куба є вершини квадратів А, В, С, D, Е, ... . Куб має шість граней, дванадцять ребер і вісім вершин.

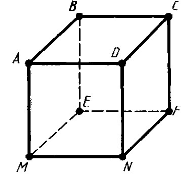
Рис.10

Залежність між числом ребер Р, числом граней Г і числом вершин В опуклого многогранника знайшов Л. Ейлер. Він довів, що

Так, для куба Г=6, В=8, Р=12, перевіряємо 8+6-12=2.

 

Контрольні запитання.

1. Що таке многогранник?
2. Як пов’язані поняття: геометричні фігури, тіла , многогранники?
3. Який многогранник називається опуклим?
4. Наведіть приклади многогранників з навколишнього середовищ, які з них опуклі, а які – не опуклі?
5. Назвіть елементи многогранника.
6. Яке твердження довів Ейлер про многогранники?
7. Чи може число ребер многогранника дорівнювати числу вершин?
8. Чи існує многогранник, у якого рівно сім ребер?

 

Правильні многогранники.

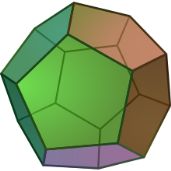
Опуклий многогранник називається правильним , якщо його грані є правильними многокутниками з однією і тією самою кількістю сторін, а в кожній вершині многогранника одне і те ж число ребер(Рис.11).

 

Рис.11

Існує 5 типів правильних опуклих многогранників(Рис.12):

• Тетраедр
• Куб (гексаедр)
• Октаедр
• Додекаедр
• Ікосаедр

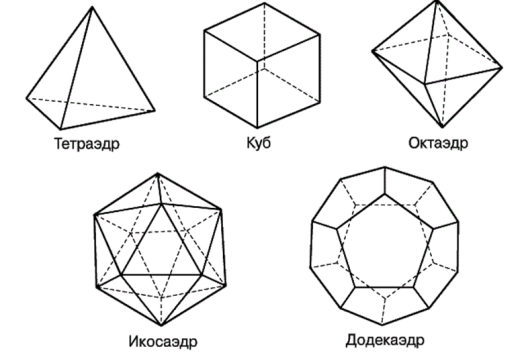
Рис.12

 

Правильні многогранники названі по імені Платона, який в творі «Тімей» (нібито IV століття до н. е.) давав їм містичний зміст, але вони були відомі і до Платона. [10]

Правильні многогранники іноді називають Платоновими тілами. Вони займали визначне місце в ідеалістичній картині світу давньогрецького філософа Платона. Чотири в них відображали чотири «суті» або «стихії»(Рис.13):

• тетраедр втілював вогонь, оскільки його вершина спрямована вгору, як у розпаленого полум’я;
• ікосаедр – як найбільш опуклий - воду,
• гексаедр(куб) – найбільш стійка із фігур – землю;
• октаедр – повітря.
• додекаедр, вважався найголовнішим, втілював в собі «все істотне», символізував все світосприйняття – весь всесвіт. [14]

Для виникнення даних асоціацій були наступні причини: жар вогню відчувається чітко і гостро (як маленькі тетраедри); повітря складається з октаедрів: його дрібні компоненти настільки гладкі, що їх насилу можна відчути, вода виливається, якщо її взяти в руку, як ніби вона зроблена з безлічі маленьких кульок (до яких найближче ікосаедр), на противагу воді, абсолютно несхожі на кулю кубики складають землю, що служить причиною того, що земля розсипається в руках, на противагу плавному току води.

З приводу п'ятого елементу, додекаедра, Платон зробив невиразне зауваження: «... його бог визначив для Всесвіту і вдався до нього в якості зразка». [15]

 

Рис.13

 

Таблиця основних параметрів правильних многогранників.

Многогранник		Вершини кутів	Ребра	Грані	Символ Шлефлі
Правильний тетраедр (чотиригранник)		4	6	4	{3, 3}
Куб (шестигранник)		8	12	6	{4, 3}
Октаедр (восьмигранник)		6	12	8	{3, 4}
Додекаедр (дванадцятигранник)		20	30	12	{5, 3}
Ікосаедр (двадцятигранник)		12	30	20	{3, 5}

 

Тетраедр.

Чотиригранник, тетраедр, трикутна піраміда — многогранник із чотирма вершинами, і з чотирма трикутними гранями, кожна вершина якого утворена трьома гранями, що утворюють тригранний кут. [10]

Рис.14

У чотиригранника 4 грані, 4 вершини і 6 ребер. Завжди є два ребра які не мають спільних вершин і не дотикаються. Паралельні площини, що проходять через ребра які не дотикаються, визначають паралелепіпед, що описаний навколо тетраедра.

Відрізок, що сполучає вершину (тригранний кут) чотиригранника з центром протилежної грані (точкою перетину медіан протилежної грані), називається медіаною чотиригранника. Відрізок, який сполучає середини ребер чотиригранника, що не дотикаються, називається бімедіаною, що сполучає дані ребра. Відрізок (перпендикуляр), що сполучає вершину чотиригранника з точкою протилежної грані і перпендикулярний цій грані, називається його висотою, опущеною з даної
вершини. [10]

Тетраедр – трикутна піраміда, всі ребра якої рівні. Всі грані – правильні трикутники, у кожній вершині сходиться по три ребра. У правильного тетраедра всі двогранні кути при ребрах і всі тригранні кути при вершинах рівні.(Рис.14)

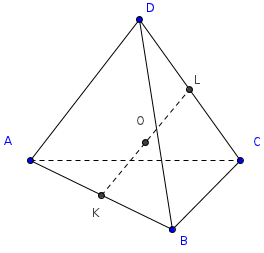
У правильного тетраедра(рис.15) з довжиною ребра a:

Рис.15

Площа поверхні 

Об'єм 

Висота 

Радіус вписаної сфери  

Радіус описаної сфери 

Кут нахилу ребра 

Кут нахилу грані 

Властивості правильного тетраедра:

• В правильний тетраедр можна вписати октаедр, притому чотири (з восьми) грані октаедра будуть суміщено з чотирма гранями тетраедра, всі шість вершин октаедра будуть суміщено з центрами шести ребер тетраедра.
• Правильний тетраедр з ребром х складається з одного вписаного октаедра (у центрі) з ребром х/2 і чотирьох тетраедрів (по вершинам) з ребром х/2.
• Правильний тетраедр можна вписати в куб двома способами, притому чотири вершини тетраедра будуть суміщено з чотирма вершинами куба. Всі шість ребер тетраедра лежатимуть на всіх шести гранях куба і дорівнюватимуть діагоналі грані-квадрата.
• Правильний тетраедр можна вписати в ікосаедр, притому, чотири вершини тетраедра будуть суміщено з чотирма вершинами ікосаедра. [10]

Правильний тетраедр має три осі симетрії, шість площин симетрії.(Рис.16)

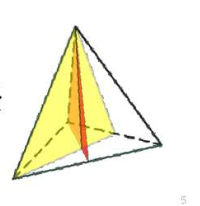
Рис.16

 

Октаедр.

Октаедр (грец. οκτάεδρον, від грец. οκτώ, «вісім» і грец. έδρα — «основа») – це дві правильні чотирикутні піраміди із спільною основою, многогранник з вісьма гранями. Правильний октаедр є одним з п'яти опуклих правильних многогранників, так званих Платонових тіл; грані правильного октаедра — вісім правильних трикутників. [10]

Правильний октаедр є двоїстим до куба. Він є повним усіканням тетраедра. Правильний октаедр є квадратною біпірамідою в кожному з трьох ортогональних напрямків. Він також є трикутною антипризмою в кожному з чотирьох напрямків.

Октаедр — тривимірний варіант більш загального поняття гіпероктаедр.

Правильний октаедр є тривимірною кулею в манхеттенській метриці.

Правильний октаедр має 8 трикутних граней, 12 ребер, 6 вершин, в кожній його вершині сходяться 4 ребра.

У октаедра грані – правильні трикутники, але у кожній вершині сходиться по чотири ребра.(Рис.17)

 

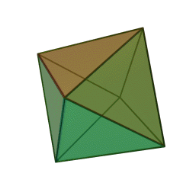
Рис.17

Розміри:

Якщо довжина ребра октаедра дорівнює а, то радіус сфери, описаної навколо октаедра (яка торкається всіх кутів), дорівнює:

радіус вписаної в октаедр сфери (яка торкається всіх граней) можна обчислити за формулою:

двогранний кут:

Радіус напіввписаної сфери (яка торкається всіх ребер) дорівнює

Площа і об'єм(Рис.18)

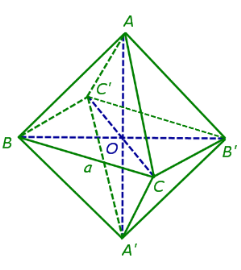
Рис.18

Площа повної поверхні правильного октаедра з довжиною ребра a дорівнює

Об'єм октаедра (V) обчислюється за формулою:

Таким чином, об'єм октаедра в чотири рази більший за об'єм тетраедра з тією ж довжиною ребра, тоді як площа поверхні вдвічі більша (оскільки поверхня складається з 8 трикутників, а у тетраедра — з чотирьох).

 

 

 

Куб.

Куб або гексаедр — правильний многогранник, кожна грань якого є квадратом. Окремий випадок паралелепіпеда і призми.(Рис.19)

У куба всі грані – квадрати, у кожній вершині сходиться по три ребра.

Куб – прямокутний паралелепіпед з однаковими ребрами.

 

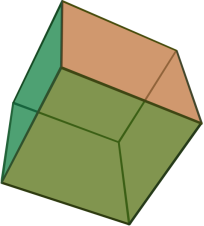
Рис.19

У куба нараховується шість квадратів. Всі вершини куба є вершинами 3-х квадратів. Сума плоских кутів у кожній вершині дорівнює 270⁰.

Кількість сторін у грані – 4.

Загальна кількість граней – 6.

Кількість ребер, які сходяться до кожної вершини – 3.

Загальна кількість вершин – 8.

Загальна кількість ребер – 12.(Рис.20)

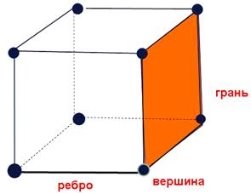
Рис.20

 

Формули:

Для куба, довжина ребер якого дорівнює a(Рис.21):

Площа поверхні  

Діагональ грані  

Радіус описаної сфери  

Радіус вписаної сфери 

Об’єм 

Просторова діагональ   

Радіус сфери, що дотична до ребер 

Кут між гранями( в радіанах) 

 

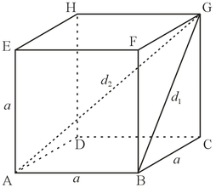
Рис.21

Властивості куба.

• В куб можна вписати тетраедр двома способами, притому чотири вершини тетраедра будуть суміщено з чотирма вершинами куба. Всі шість ребер тетраедра лежатимуть на всіх шести гранях куба і дорівнюватимуть діагоналі грані-квадрата.
• Чотири перетини куба є правильними шестикутниками — ці перетини проходять через центр куба перпендикулярно чотирьом його діагоналям.
• У куб можна вписати октаедр, притому всі шість вершин октаедра будуть суміщено з центрами шести граней куба.
• Куб можна вписати в октаедр, притому всі вісім вершин куба будуть розташовано в центрах восьми гранях октаедра.
• У куб можна вписати ікосаедр, при цьому, шість взаємно паралельних ребер ікосаедра будуть розташовані відповідно на шести гранях куба, решта 24 ребра всередині куба, всі дванадцять вершин ікосаедра лежатимуть на шести гранях
  куба. [10]

Елементи симетрії куба.

Вісь симетрії куба може проходити або через середини ребер, які паралельні, не належать ні одній із граней або через точку перетину діагоналей протилежних граней. Центр симетрії куба є точка перетину діагоналей куба.(Рис.22)

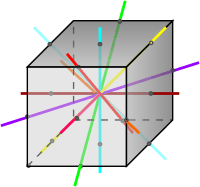
Рис.22

Через центр симетрії куба проходить 9 осей симетрії. Площини симетрії в куба теж 9, вони проходять або через протилежні ребра (їх  6), або через середини протилежних ребер ( їх 3).(Рис.23)

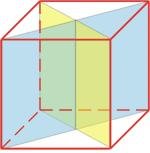
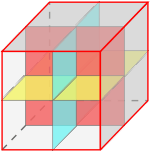
Рис.23

Додекаедр.

Рис.24

Додекаедр (від грец. Δώδεκα — дванадцять і грец. ἕδρα — грань), дванадцятигранник — правильний многогранник, об'ємна геометрична фігура, складена з дванадцяти правильних п'ятикутників. Кожна вершина додекаедра є вершиною трьох правильних п'ятикутників. Таким чином, додекаедр має 12 граней (п'ятикутних), 30 ребер і 20 вершин (у кожній сходяться 3 ребра). Сума плоских кутів при кожній з 20 вершин рівна 324°.[10]

У додекаедра грані – правильні п'ятикутники, у кожній його вершині сходиться по три ребра.

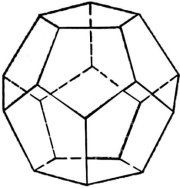
Рис.25

Формули для додекаедра зі стороною а:

Площа поверхні  

Об’єм  

Радіус описаної сфери  

Радіус вписаної сфери  

Двогранний кут між гранями  

Властивості:

• Усі двадцять вершин додекаедра лежать по п'ять у чотирьох паралельних площинах, утворюючи в кожній з них правильний п'ятикутник.
• Двогранний кут між будь-якими двома суміжними гранями додекаедра дорівнює arccos (-1 / √5) ≈116 °, 565.
• Сума плоских кутів при кожній з 20 вершин дорівнює 324 °, тригранний кут дорівнює arccos (-11 / 5√5) ≈2,9617 стерадіан.
• У додекаедр можна вписати куб так, що сторони куба будуть діагоналями додекаедра.
• Додекаедр має три зірчасті форми. [10]

 

 

Ікосаедр.

Рис.26

Ікосаедр (від грец. εικοσάς, «двадцять» і грец. —εδρον, «грань», «лице», «основа») — правильний опуклий многогранник, двадцятигранник, одне з Платонових тіл. Кожна з 20 граней є рівностороннім трикутником. Число ребер рівне 30, число вершин —12. [10]

Формули ікосаедра з довжиною ребра а(Рис.27):

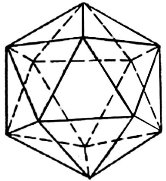
Рис.27

Площа 

Об’єм 

Радіус вписаної кулі 

Радіус описаної кулі 

 

Властивості:

•                  Ікосаедр можна вписати в куб, при цьому його шість взаємно паралельних ребер розташовуватимуться відповідно на шести гранях куба, решта 24 ребра - усередині куба, а усі дванадцять вершин ікосаедра лежатимуть на шести гранях куба.
•                  В ікосаедр може бути вписаний тетраедр, притому чотири вершини тетраедра будуть суміщені з чотирма вершинами ікосаедра.
•                  Ікосаедр можна вписати в додекаедр, притому вершини ікосаедра будуть суміщені з центрами граней додекаедра.
•                  У ікосаедр можна вписати додекаедр, притому вершини додекаедра будуть суміщені з центрами граней ікосаедра. [10]

 

Контрольні запитання.

1. Який многогранник називається правильним?
2. Назвіть всі правильні многогранники.
3. Як називається правильний чотиригранник? Скільки він має вершин, ребер та граней?
4. Як називається правильний шестигранник? Скільки він має вершин, ребер та граней?
5. Як називається правильний восьмигранник? Скільки він має вершин, ребер та граней?
6. Як називається правильний дванадцятигранник? Скільки він має вершин, ребер та граней?
7. Як називається правильний двадцятигранник? Скільки він має вершин, ребер та граней?
8. Чи вірно, що опуклий многогранник є правильним, якщо його грані – правильні многокутники?

 

 

Призма.

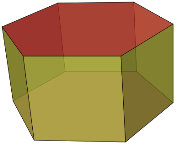
Рис.28

Призмою називається многогранник (призматоїд), у якого дві грані — рівні n-кутники, розташовані в паралельних площинах, а решта n граней — парале-
лограми. [10]

Призма – це многогранник, який складається з двох плоских многокутників, що лежать у різних площинах та суміщаються паралельним перенесенням, і всіх відрізків, що сполучають відповідні точки даних многокутників.

Основами призми є плоскі многокутники, ребрами призми є відрізки, що сполучають відповідні точки многокутників.

Висотою призми є відстань між основами. Діагоналлю призми є відрізок, що сполучає дві вершини призми і не належить жодній із граней.

Діагональні перерізи — це перерізи призми площинами, що проходять через два бічних ребра, які не належать одній грані.

Властивості призми:

• основи призми рівні;
• основи призми лежать у паралельних площинах;
• бічні ребра призми паралельні і рівні. [17]

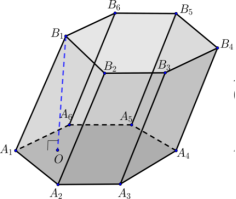
Рис.29

Відповідно на рис.29,:

А₁…А₆В₁…В₆ – призма;

А₁…А₆  та В₁…В₆ – основи призми;

А₁В₁, …, А₆В₆ – ребра призми;

А₁А₂В₂В₁, …, А₁А₆В₆В₁ – бокові грані призми;

А₁, …, А₆ , В₁, …, В₆ – вершини;

ОВ₁ – висота призми.

 

Класифікація призм:

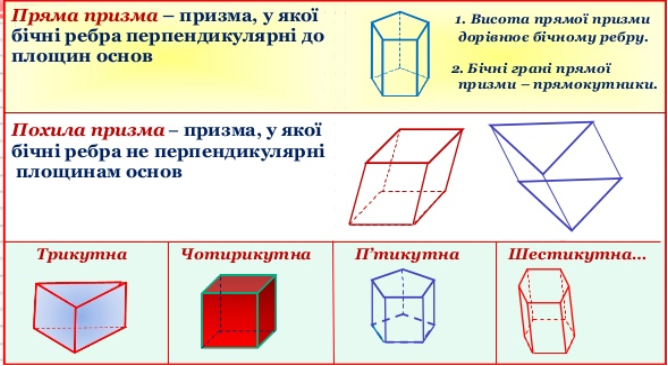
Призма називається прямою, якщо її бічні ребра перпендикулярні до основи. Інші призми — похилі.

Призма називається правильною, якщо вона пряма і її основи — правильні багатокутники.

Види призм:

Паралелепіпед‎.

Паралелепіпед (від грец. Παράλλος — паралельний і επιπεδον — площина) — призма(Рис.30), основою для якої є паралелограм. [10]

Рис.30

Розрізняють декілька типів паралелепіпедів:

• Прямий паралелепіпед — паралелепіпед, бічні ребра якого перпендикулярні до площини основи. У прямих паралелепіпедів чотири грані є прямокутниками, а
  основи — паралелограмами(Рис.31). Паралелепіпеди, які не є прямими, називаються похилими(Рис.32).

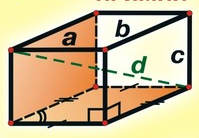
Рис.31

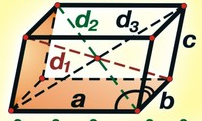
Рис.32

• Прямокутний паралелепіпед — прямий паралелепіпед, основою якому є прямокутник.  У прямокутного паралелепіпеда всі грані — прямокутники.  Довжини трьох ребер прямокутного паралелепіпеда, що мають спільну вершину, називають його вимірами(Рис.33).  Всі чотири діагоналі прямокутного паралелепіпеда рівні.  Моделями прямокутного паралелепіпеда може бути кімната, цеглина, сірникова коробка. [10]

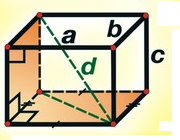
Рис.33

• Куб — прямокутний паралелепіпед з рівними сторонами. Всі шість граней куба — рівні квадрати(Рис.34).

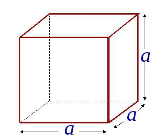
Рис.34

Формули:

• Прямий паралелепіпед

Площа бічної поверхні:

S_б = Р_о · h, де Р_о — периметр основи, h — висота.

Площа повної поверхні:

S_п = S_б + 2S_о, де S_о — площа основи.

Об'єм паралелепіпеда дорівнює добутку площі його основи на висоту:

V = S_о · h.

• Прямокутний паралелепіпед

Площа бічної поверхні:

S_б = 2c (a + b), де a, b — сторони основи, c — бічне ребро прямокутного паралелепіпеда.

Площа повної поверхні:

S_п = 2(ab + bc + ac).

Об'єм:

V = abc, де a, b, c — виміри прямокутного паралелепіпеда.

У прямокутному паралелепіпеді квадрат діагоналі d дорівнює сумі квадратів його вимірів:

d² = a² + b² + c².

• Куб

Площа повної поверхні:

S_п = 6a², де a — сторона.

Об'єм:

V = a³.

Діагональ:

d = a√3.

Властивості призм:

Паралелепіпед:

1.               Усі грані паралелепіпеда — паралелограми.
2.               Протилежні грані — паралельні та рівні.
3.               Усі діагоналі перетинаються в одній точці (центр паралелепіпеда) й поділяються нею навпіл.
4.               Точка перетину діагоналей паралелепіпеда і точки перетину діагоналей основ лежать на одній прямій.
5.               Сума квадратів діагоналей дорівнює сумі квадратів усіх ребер.

Пряма призма:

1.               Бічні ребра перпендикулярні до основи.
2.               Усі бічні грані — прямокутники.
3.               Бічне ребро є висотою призми.

Правильна призма:

1.               Основа — правильний багатокутник.
2.               Бічні ребра перпендикулярні до основи.
3.               Усі бічні грані — прямокутники.
4.               Бічне ребро є висотою призми.

Об'єм:

Об'єм призми дорівнює добутку площі основи на висоту. Таким чином об'єм дорівнює: 

де S — площа основи, h — висота.

Об'єм правильної призми в основі якої є правильний n-кутник дорівнює:

 

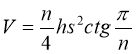
Площа поверхні:

Площа бічної поверхні призми дорівнює , де P — периметр основи, H — висота.

Площа поверхні призми дорівнює  , де S — площа основи, h — висота, P— периметр основи.

Площа поверхні правильної призми в основі якої є правильний n-кутник дорівнює:

 

Контрольні запитання.

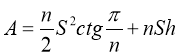
1. Що таке призма?
2. Назвіть елементи призми.
3. Які бувають види призм?
4. Чи може призма мати чотири грані?
5. Які призми називають прямими?
6. Які призми називають правильними?
7. Чи є призма правильною, якщо: а) рівні всі її бічні ребра; б) всі бічні грані – прямокутники?
8. Чи вірно, що правильна чотирикутна призма є прямокутним паралелепіпедом?
9. Чому дорівнює площа бічної поверхні прямої призми?
10. Чому дорівнює площа поверхні довільної призми?
11. Сформулюйте означення паралелепіпеда. Назвіть його елементи.
12. Які бувають паралелепіпеди?
13. Який паралелепіпед називається прямим?

 

 

Піраміда.

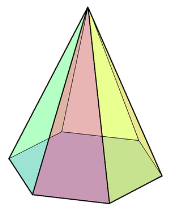
Рис.35

Пірамідою називається многогранник, який складається з плоского многокутника - основи піраміди, точки, яка не лежить у площині основи — вершини піраміди, і всіх відрізків, що сполучають вершину піраміди з точками основи( Рис.35). 

Поверхня піраміди складається з основи і бічних граней. Кожна бічна грань — трикутник. Однією з його вершин є вершина піраміди, а протилежною стороною — сторона основи піраміди.

Висотою піраміди є перпендикуляр, опущений з вершини піраміди на площину основи.

Піраміда називається n-кутною, якщо її основою є n-кутник. Для трикутної піраміди існує власна назва — чотиригранник.

Надалі розглядатимемо лише піраміди з опуклим багатокутником в основі. Такі піраміди називаються опуклими многогранниками.

Правильна піраміда (довершена) — якщо її основою є правильний багатокутник, центр якого збігається з основою висоти піраміди. Бічна поверхня правильної піраміди дорівнює добутку півпериметра основи на апофему.

Вісь правильної піраміди — пряма, яка містить її висоту. У правильній піраміді бічні ребра рівні між собою, а бічні грані — рівні рівнобедрені трикутники.

Висота бічної грані правильної піраміди, проведена з її вершини, називається апофемою. Бічною поверхнею піраміди називається сума площ її бічних граней.

Елементи піраміди(Рис.36):

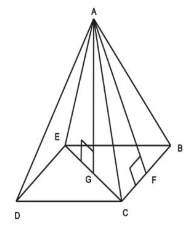
Рис.36

ABCDE – піраміда;

A – вершина піраміди (точка, яка не належить площини основи та з’єднує бокові ребра).

BCDE – основа піраміди (багатокутник. Якому не належить вершина піраміди);

AG – висота піраміди (відрізок перпендикуляра, який проведено через вершину піраміди до площини її основи, кінцями цього відрізку є вершина піраміди та основа перпендикуляру);

AF – апофема (висота бокової грані правильної піраміди, яка проведена з її вершини);

ACE - діагональний переріз (переріз піраміди, який проходить через вершину та діагональ основи);

ABC, ACD, ADE, AEB – бокові грані піраміди (трикутники, які сходяться до вершини піраміди);

AB, AC, AD, AE –  бокові ребра піраміди (спільні сторони бокових граней).

Види пірамід:

Правильна піраміда.

Піраміда називається правильною, якщо основою її є правильний багатокутник, а вершина проектується в центр основи. Тоді вона має такі властивості:

Бічні ребра правильної піраміди рівні;

В правильній піраміді всі бічні грані - конгруентні трикутники;

В будь-яку правильну піраміду можна як вписати, так і описати навколо неї сферу;

Якщо центри вписаної і описаної сфери збігаються, то сума плоских кутів при вершині піраміди дорівнює π, а кожен з них відповідно π/n, де n - кількість сторін багатокутника основи;

Площа бічної поверхні правильної піраміди дорівнює половині добутку периметра основи на апофему.

Прямокутна піраміда.

Піраміда називається прямокутною, якщо одне з бічних ребер піраміди перпендикулярне основі. В даному випадку, це ребро і є висотою піраміди.

Тетраедр.

Тетраедром називається трикутна піраміда. У тетраедра кожна з граней може бути прийнята за основу піраміди. Крім того, існує велика різниця між поняттями «правильна трикутна піраміда» і «правильний тетраедр». Правильна трикутна піраміда - це піраміда з правильним трикутником в основі (межі ж повинні бути рівнобічними трикутниками). Правильним тетраедром є тетраедр, у якого всі грані є рівносторонніми трикутниками.

Формули:

Площа бічної поверхні правильної піраміди дорівнює добутку половини периметра (півпериметру) основи на апофему:

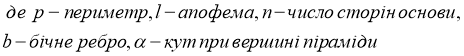
Площа поверхні правильної піраміди дорівнює сумі площ бічної поверхні та основи:

Об'єм піраміди дорівнює одній третій добутку площі її основи S на висоту h:

 

Контрольні запитання.

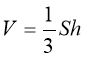
1. Сформулюйте означення піраміди.
2. Назвіть її елементи.
3. Які бувають піраміди?
4. Що таке висота піраміди?
5. Чи може висота піраміди збігатися з висотою однієї з бічних граней?
6. Які піраміди називають правильними?
7. Що таке апофема правильної піраміди?
8. Чому дорівнює площа бічної поверхні правильної піраміди?
9. Чому дорівнює площа поверхні правильної піраміди?
10. Як можна визначити об’єм піраміди?

 

 

Тіла обертання

Уявіть, що плоский многокутник AВCDE обертається навколо нерухомої прямої АВ (Рис. 37, а). При цьому кожна його точка, що не лежить на прямій АВ, описує коло з центром на цій прямій, а весь многокутник AВCDE описує деяке тіло обертання (Рис. 37, б). Пряма АВ - вісь цього тіла. [3]

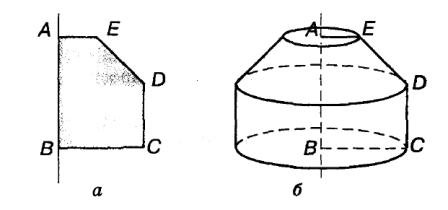
Рис.37

Тіла́ обертання — об'ємні тіла, що виникають при обертанні плоскої фігури, обмеженої кривою, навколо осі, що лежить в тій же площині(Рис.38).

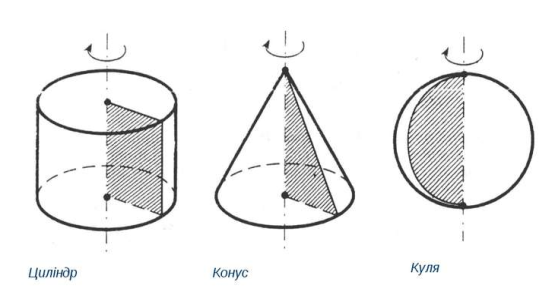
Рис.38

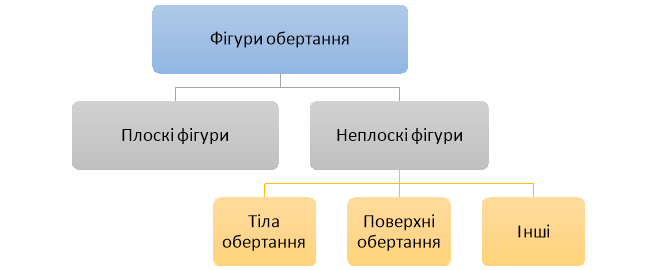
Рис.39

Слід розрізняти тіла обертання та фігури обертання. Остання поняття – загальніше (Рис.39).

 

Циліндр.

Циліндр (грец. Κύλινδρος — «валик») — геометричне тіло, обмежене замкнутою циліндричною поверхнею і двома паралельними площинами, що перетинають її[10].( Рис.40)

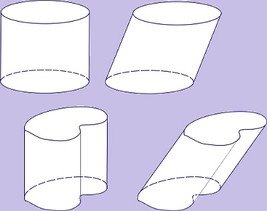
Рис.40

Циліндром називається тіло, що складається з двох кругів, які не лежать в одній площині і суміщаються паралельним перенесенням, і всіх відрізків, що сполучають відповідні точки цих кутів. Круги називаються основами циліндра, а відрізки, що сполучають точки кіл кругів, – твірними циліндра. Основи циліндра рівні, твірні циліндра паралельні і рівні. Радіусом циліндра називається радіус його основи. Висотою циліндра називається відстань між площинами його основ. Віссю циліндра називається пряма, яка проходить через центри основ. [9]

Найпростішим тілом обертання є циліндр.

Круговим циліндром називають тіло, утворене обертанням прямокутника навколо його сторони (Рис.41).

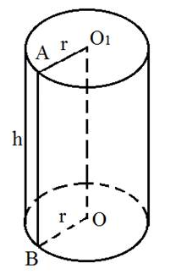
Рис.41

Якщо прямокутник АВОО₁ обертати навколо сторони ОО₁ , то його сторони АО₁ та ВО опишуть рівні круги, які називають основами циліндра. Сторона АВ опише бічну поверхню циліндра. Кожен відрізок цієї поверхні, твірна циліндра, яка дорівнює АВ. Довжина твірної є висотою циліндра.

Елементи циліндра( Рис.42):

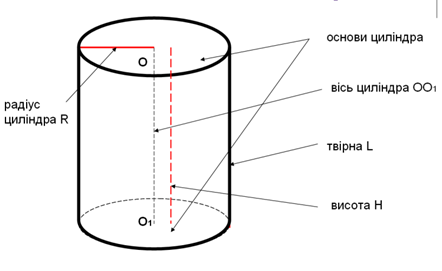
Рис.42

Перерізи циліндра.

• Осьовий переріз циліндра( Рис43).

Переріз циліндра площиною, яка проходить через вісь циліндра, називається осьовим перерізом[19] ( Рис.43).

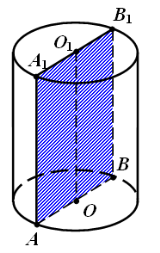
Рис.43

АА₁В₁В - осьовий переріз циліндра, ОО₁ - вісь циліндра.

Всі осьові перерізи – рівні прямокутники.

• Переріз циліндра площиною, паралельною до осі( Рис.44).

Переріз циліндра площиною, яка паралельна до його осі, є
прямокутник ( Рис.44).

Дві його сторони – твірні циліндра, а дві інші – паралельні хорди основ[19].

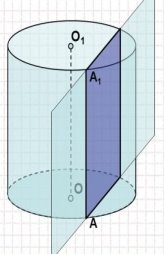
Рис.44

• Переріз циліндра площиною, перпендикулярною до осі ( Рис.45).

Площина, перпендикулярна до осі циліндра, перетинає його бічну поверхню по колу, яке дорівнює колу основи[19].

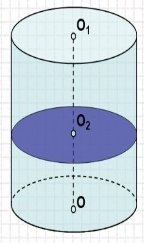
Рис.45

• Переріз циліндра площиною, не перпендикулярною до осі ( Рис.46).

Площина, не перпендикулярна до осі та не паралельна основам циліндра, перетинає його бічну поверхню по еліпсу[19].

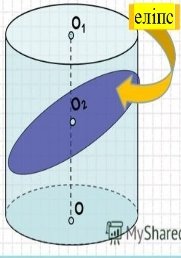
Рис.46

Формули.

Площа поверхні:

Площа бічної поверхні:

Площа повної поверхні:

Об'єм:

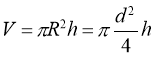
Де d — діаметр основи; R — радіус основи.

 

Контрольні запитання.

1. Як можна утворити тіло обертання?
2. Що таке вісь обертання?
3. Що таке осьовий переріз тіла обертання?
4. Як пов’язані між собою фігури обертання і тіла обертання?
5. Що таке циліндр?
6. Назвіть його елементи.
7. Які перерізи циліндра ви знаєте?
8. Якою фігурою є осьовий переріз циліндра?
9. Якою фігурою є переріз циліндра площиною, перпендикулярною до його осі?
10. Якою фігурою є переріз циліндра площиною, паралельною його осі?
11. Як можна визначити площу бічної поверхні циліндра?
12. Як можна визначити площу повної поверхні циліндра?
13. Як можна визначити об’єм циліндра?

 

 

Конус.

Конус — геометричне тіло, отримане шляхом об'єднання всіх променів, що виходять з однієї точки — вершини конуса, і таких що проходять через довільну плоску криву ( рис.47). Іноді конусом називають частину такого тіла, отриману об'єднанням усіх відрізків, що з'єднують вершину і точки пласкої поверхні (яку в такому випадку називають основою конуса, а конус називають таким, що спирається на дану поверхню). Надалі буде розглядатися саме цей випадок, якщо не сказано про інше. [10]

За ДСТУ: конус — узагальнений термін, під яким залежно від конкретних умов розуміють конічну поверхню, конічну деталь чи конічний елемент[10].

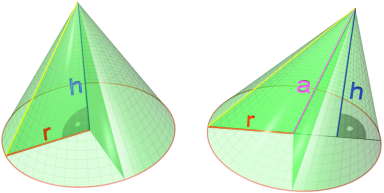
Рис.47

Відрізок, опущений перпендикулярно з вершини на площину основи (а також його довжина), називається висотою конуса. Якщо площа основи має скінченне значення, то об'єм конуса також має скінченне значення і дорівнює третині добутку висоти на площу основи. Таким чином всі конуси, що спираються на дану основу, і мають вершину в площині, паралельній цій основі, мають рівний об'єм, оскільки їх висоти рівні. Якщо основою конуса є многокутник, тоді конус стає пірамідою. Таким чином піраміди є підмножиною конусів[10].

Відрізок, що сполучає вершину конуса з точкою границі його основи називається твірною конуса. Множина всіх твірних конуса називається бічною поверхнею конуса[10].

Якщо основа конуса має центр симетрії (наприклад, є еліпсом) і ортогональна проекція вершини конуса на його основу збігається з цим центром, то конус називається прямим. При цьому пряма, що сполучає вершину конуса з центром його основи називається віссю конуса. Якщо ж ортогональна проекція вершини не збігається з центром основи, то такий конус називається косим[10].

Види конусів (Рис48):

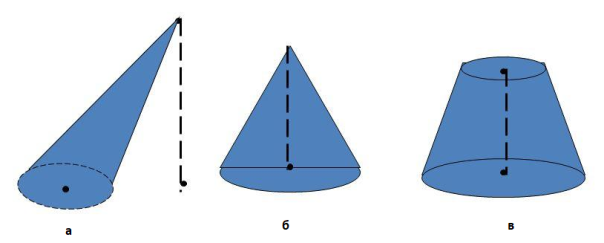
Рис.48

а) похилий конус;

б) прямий конус;

в) зрізаний конус.

Якщо основою конуса є круг, то конус називають круговим. Прямий круговий конус (часто його називають просто конусом) можна отримати обертанням прямокутного трикутника навколо одного з катетів, який таким чином стане віссю конуса ( Рис.49).

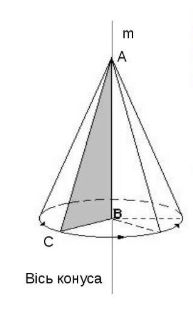
Рис.49

Конусом називають фігуру, утворену обертанням прямокутного трикутника навколо прямої m (осі), що містить катет (АВ) цього трикутника.

Висотою конуса називається перпендикуляр, опущений з його вершини на площину основи (АВ). У прямого конуса основа висоти (АВ) збігається з центром (В) основи.

Віссю прямого конуса називається пряма, яка містить його висоту.

Гіпотенуза АС утворює конічну поверхню і є твірною конуса. Інший катет ВС, що утворює круг, є радіусом конуса.

Вершина А – вершина конуса, В – центр основи конуса. [17]

Елементи конуса ( Рис.50):

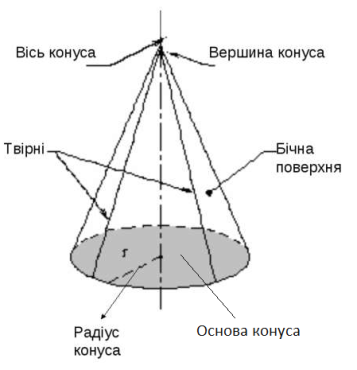
Рис.50

Перерізи конуса.

• Перерізи конуса площиною, яка проходить через вершину S конуса (Рис 51.)

Якщо площина проходить через вершину конуса, то вона перетинає бічну поверхню або в одній точці (1),  або по двом її твірним (2), або має з поверхнею одну спільну твірну, тобто дотикається до даної поверхні (3). [19]

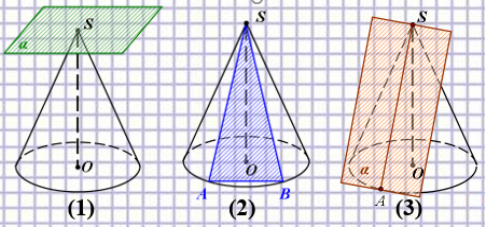
Рис.51

 

• Осьовий переріз конуса ( Рис.52).

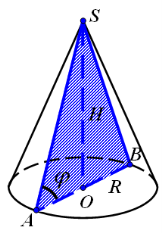
Рис.52

• Переріз конуса площиною, паралельною до основи ( Рис.53).

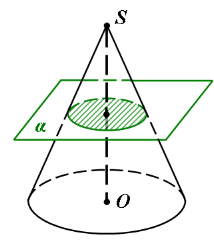
Рис.53

Формули.

Площа поверхні конуса:

Повна площа прямого кругового конуса

де r та l — радіус кола основи та довжина твірної бічної поверхні відповідно.

Площа бічної поверхні прямого кругового конуса

де r та l — радіус кола основи та довжина твірної бічної поверхні відповідно.

Об'єм конуса:

У загальному випадку:

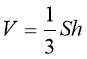
де S — площа основи, h — висота конуса.

Об'єм кругового конуса, відповідно:

 

Контрольні запитання.

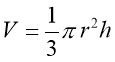
1. Сформулюйте означення конуса.
2. Що таке вершина, основа, твірна, вісь, висота конуса?
3. Чи може твірна конуса бути перпендикулярною до його висоти?
4. Назвіть перерізи конуса.
5. Якою фігурою є осьовий переріз конуса?
6. Якою фігурою є переріз конуса площиною, перпендикулярною до його осі?
7. Як можна обчислити площу бічної поверхні конуса?
8. Як можна обчислити площу поверхні конуса?
9. Що таке зрізаний конус?
10. Як можна обчислити об’єм конуса?

 

 

Куля. Сфера.

Куля — тіло, утворене обертанням круга навколо його діаметра. ( Рис.54)

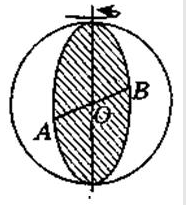
Рис.54

Центром кулі називають центр круга, обертанням якого її утворено. Відрізок, який сполучає центр кулі з довільною точкою її поверхні, — радіус кулі. Відрізок, який сполучає дві довільні точки поверхні кулі, — її хорда. Хорда кулі, яка проходить через центр, — діаметр кулі. 10 ( Рис.55)

Рис.55

Куля — це множина всіх точок простору, що перебувають від заданої точки O на відстані, не більшій за дану відстань R. При цьому точка O називається центром, а R — радіусом кулі. Будь-який відрізок, який сполучає центр кулі з точкою кульової поверхні, також називається радіусом. [10]

Площина, яка проходить через центр кулі, називається діаметральною площиною. Переріз кулі діаметральною площиною називається великим кругом, а переріз сфери – великим колом. [1]

Поверхня кулі називається сферою. Також дуже часто кулею називають частину простору, обмежену сферою. [10]

Формули.

Площа сфери:

Об’єм кулі:

 

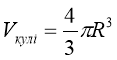
Частини кулі.

Зеленим кольором позначено сектор, сірим — сегмент, жовтим — зріз
кулі[10].( Рис. 56)

Сегмент кулі — це та її частина, що утворюється внаслідок перерізу площиною.

Зріз (кульовий шар) — це стереометричне тіло, утворене перерізами кулі двома паралельними площинами.

Сектор складається з кульового сегмента та конуса, основа якого збігається з основою сегмента, а вершина — з центром кулі. [10]

Рис.56

Контрольні запитання.

1. Що таке куля?
2. Назвіть її елементи.
3. Які частини кулі ви знаєте?
4. Що таке сфера? Назвіть її елементи.
5. Що таке діаметральна площини кулі?
6. Чи може перерізом кулі бути еліпс?
7. Як можна знайти площу поверхні кулі?
8. Як можна обчислити об’єм кулі?

 

 

Приклади розв’язування типових задач.

Задача 1.

Дано: АВСА₁В₁С₁ –правильна трикутна призма; АК=КВ, А₁М=МВ₁, в чотирикутник КМС₁С можна вписати коло.

Знайти: .

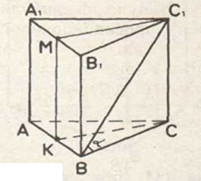Розв’язання.

КМС₁С – квадрат. Нехай С₁С=КС=а, тоді

,

,

.

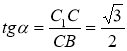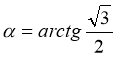Відповідь:

 

Задача 2.

Дано: ABCDA₁B₁C₁D₁ – правильна чотирикутна призма.

Знайти:

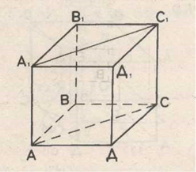Розв’язання.

 

 

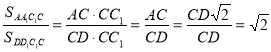
Відповідь:

 

 

 

Задача 3.

Дано:AC₁ – правильна чотирикутна призма, S_б=16, P_ABCD=16.

Знайти: S_п,,  AA₁.

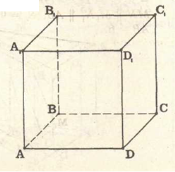Розв’язання.

4AD=16, AD=4; S_n=S_б+S_осн,

S_б = Р_ABCD*AA₁, звідки AA₁=1,

S_n=16+32=48.

Відповідь: 48, 1.

 

 

Задача 4.

Дано: DABC - правильна трикутна піраміда, , AB=3*DO.

Знайти:

Розв’язання.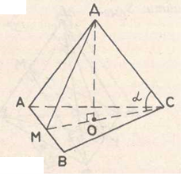

Нехай DO = a , тоді AB = 3a,

Відповідь:

 

Задача 5.

Дано: DABC - правильна трикутна піраміда, , DC = 5, DO = 3.

Знайти: S_б

Розв’язання.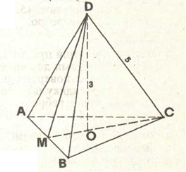

,

Відповідь:

 

Задача 6.

Дано: KABCD – правильна чотирикутна піраміда, _,

_{, , .}

Знайти: AD.

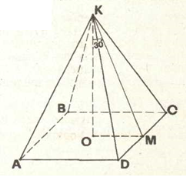Розв’язання.

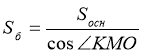, , тоді ,

, , звідки

, AD²=16,  AD = 4.

Відповідь: 4.

 

Задача 7.

Дано: KABCD – правильна чотирикутна піраміда, ABCD – квадрат,

,  KB = 3, AB = 4.

Знайти:  S_п.

Розв’язання.

,

S_п=S_б+S_осн=2S_ABK+S_осн+2S_AKD= 12+20+16=48

Відповідь: 48.

Задача 8.

Радіус основи циліндра 2 м, висота 3 м. Знайти діагональ осьового перерізу.

Дано: циліндр, ABCD - осьовий переріз, O₁C=O₁D=2м - радіус основи,

AC=BD=3м - висота циліндра.

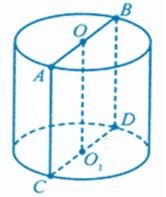Знайти: BC.

Розв’язання.

ABCD – прямокутник, CD=2O₁C=2*2=4(м).

З ∆ADC(прямокутний) за т. Піфагора

Відповідь: 5м.

 

 

 

Задача 9.

Висота конуса 6 см, радіус основи 8 см. Знайти площу діагонального перерізу конуса.

Дано: конус, SO = 6 см - висота, SA = SB = 10 см - твірна, ∆ASB - осьовий переріз конуса.

Знайти: S_ASB.

Розв’язання.

З ∆ASO- прямокутний за т. Піфагора

Відповідь: 48 см².

 

 

Задача 10.

Дано: куля, довжина кола діаметрального перерізу C=6π.

Знайти: : S _{перерізу} ,  V_кулі.

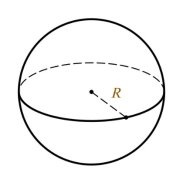Розв’язання.

C=2πR ,

S _{перерізу} =πR² , S _{перерізу} =π*3²=9π

Відповідь: 9π, 36π.

 

Задача 11.

Дано: прямий круговій циліндр, ABCD - осьовий переріз, _{, .}

Знайти: S_б.

Розв’язання.

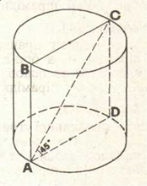. Оскільки  , то . , звідки R = 1, H = 2.  .

 

Відповідь: 4π.

 

Список використаних джерел.

1. О.М. Афанасьєва, Я.С. Бродський, Павлов О.Л., А.К. Сліпенко, Математика (підручник для студентів ВНЗ І - ІІ р. а.) – К. ; Вища школа, 2002
2. Г.П. Бевз, В.Г. Бевз, Математика: 11кл.: підручник для загальноосвітніх навчальних закладів: рівень стандарту – К.: Генеза, 2012
3. Г.П. Бевз, В.Г. Бевз, Н.Г. Владімірова, Геометрія: підручник для 10-11 кл. загальноосвітніх навчальних закладів  – К.: «Вежа», 2002
4. О.Г. Гайштут, Г.М. Литвиненко, Геометрія-це нескладно. Стереометрія. Навчально-методичний посібник – К.: «Магістр-S», 1997
5. О.Г. Гайштут, Р.П. Ушаков, Математика. Збірник задач з математики. 7-11 класи.
6. М.І. Резніченко, Основи математики – К., НУХТ, 2008 (навчальне видання).
7. М.І. Шкіль, та ін. Алгебра і початки аналізу. Підручник для 10 – 11 кл. ЗНО – К., Освіта, 2005
8. http://moyaosvita.com.ua/geometriya
9. http://allreferat.com.ua/uk/pedagogika_metoduka_vukladanny/referat/4061
10. https://uk.wikipedia.org/wiki/
11. http://shkola.ua/uchebniki/read/560a590dfd7207a528a0c0f2?page=64
12. http://www.myshared.ru/slide/1345263/
13. https://en.ppt-online.org/310679
14. http://www.myshared.ru/slide/1222550/
15.  http://ito.vspu.net/ENK/2011- 2012/kompleks_new_magistru/rob_styd/14_15/astanina/
16. http://www.subject.com.ua/mathematics/zno/497.html
17. http://shkolyar.in.ua/mnogogrannyly/pryzma
18. http://osvita.ua/school/lessons_summary/math/33472/
19. http://oipopp.ed-sp.net
20. http://svitppt.com.ua/images/9/8462/770/img4.jpg