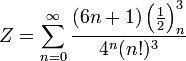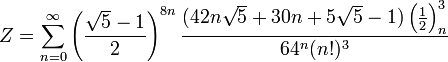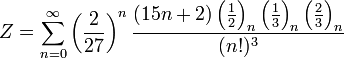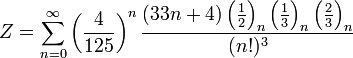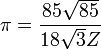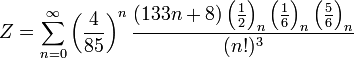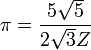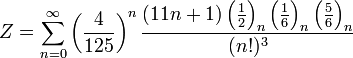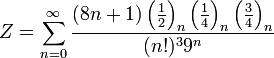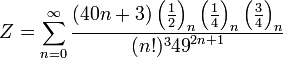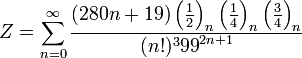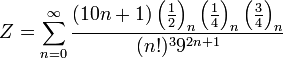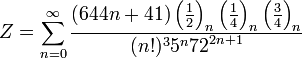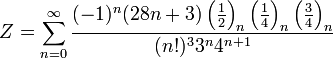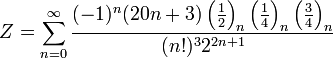Методичний посібник " Число Пі "

Про матеріал

Що ж це за число таке, що вже майже п’ять тисячоліть примушує людей важко трудитися і витрачати життя для того, щоб додати до його «хвоста», чи запам’ятати зайву цифру? У даному посібнику ви зможете знайти відповіді на ваші запитання.

Перегляд файлу

ПІВ ЦАРСТВА ЗА ОДНУ ЦИФРУ

ЦІКАВЕ ЧИСЛО ПІ

Що ж це за число таке, що вже майже п’ять тисячоліть примушує людей важко трудитися і витрачати життя для того, щоб додати до його «хвоста», чи запам’ятати зайву цифру

Зміст

І. Вступ

ІІ. Число Пі

ІІІ. Ірраціональність і трансцендентність

ІV. Співвідношення

V. Історія розрахунків

1. Античність

2 Друге тисячоліття нашої ери

3. Обчислення в епоху комп'ютерів

4. Подання у вигляді ланцюгового дробу

5. Наближення

VІ. Застосування числа Пі

VІІ. День числа

VІІІ. Цікаві факти про число Пі.

Вступ

Чи ніколи ми не ставили собі питання, чому число Пі так називається? Ну якщо ж дати на це питання відповідь, то воно походить від грецького слова «вимірюю навколо», яке починається з букви Пі.

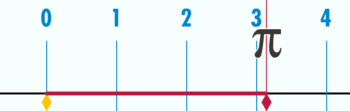
Число Пі виражає відношення довжини кола до діаметру і приблизно дорівнює 3,14. Вперше його позначив грецькою буквою π британець Вільям Джонс у праці «Огляд досягнень математики», надрукованій в 1706 році. Він керувався тим, що з неї починається слово περιμετρέο – «вимірюю навколо». Стара назва - лудольфове число, а загальноприйнятим воно стало після робіт Леонарда Ейлера у 1737 році.

Широке поширення це позначення отримало завдяки великому математику Леонарду Ейлеру (1707-1783), який часто ним користувався. Як і коли було відкрито саме число, невідомо. Те, що відношення довжини кола до його діаметра – число постійне, відомо ще з давніх часів. Вавилоняни в III тисячолітті до н. е. вже знали, що Пі дорівнює трохи більше трьох. Обчислити значення цього числа з точністю до трьох знаків вдалося лише в III столітті до н. е. Архімеду. А в XVIII столітті Йоганн Ламберт довів, що Пі не можна виразити у вигляді відношення двох цілих чисел, тобто у вигляді кінцевого або періодичного десяткового дробу. На час Ламберта Пі вже було обчислено з точністю до ста з гаком знаків. А влітку 2010 року була досягнута точність 5 трлн знаків. Пі - ірраціональне число, тобто його значення не може бути точно виражено у вигляді дробу. Отже, його десяткове подання ніколи не закінчується і не є періодичним. Ірраціональність числа Пі була вперше доведена Іоганном Ламбертом в 1761 році.
Історія числа Пі йшла паралельно з розвитком всієї математики. Деякі автори розділяють увесь процес на 3 періоди: стародавній період, протягом якого π вивчався з позиції геометрії, класична ера, що прослідувала за розвитком математичного аналізу в Європі в XVII столітті, і ера цифрових комп`ютерів.
Ще в давнину люди широко користувалися цим числом, будуючи піраміди, проводячи зрошувальні системи, стягуючи податки. У Вавилоні це співвідношення виражали чомусь числом три. Чому? Невідомо. Але воно виявилося правильним!

Число пі.

Число́ пі (позначається $\pi$ ) —математична константа, що визначається у Евклідовій геометрії як відношення довжини кола до його діаметра .

$\pi = \frac{l}{d}$

або як площа круга одиничного радіуса.

Число $\pi$ виникло в геометрії як відношення довжини кола до довжини його діаметра, проте воно з'являється і в інших областях математики. Вперше позначенням цього числа грецькою літерою π скористався британський математик Джонс (1706), а загальноприйнятим воно стало після робіт Ейлера. Це позначення походить від початкової букви грецьких слів περιφέρεια — оточення, периферія та περίμετρος — периметр.

Довжина кола дорівнює π, якщо його діаметр 1.

Ірраціональність і трансцендентність

Число $\pi$ ірраціональне і трансцендентне.

Ірраціональність числа $\pi$ була вперше доведена Йоганном Ламбертом у 1767 році шляхом розвинення числа $\frac{e-1}{2^n}$ у неперервний дріб. У 1794-му Лежандр навів строгіше доведення ірраціональності чисел π і π².

У 1882 році професорові Кенігсберзького, пізніше Мюнхенського університетів Фердинанду Ліндеману вдалося довести трансцендентність числа π. Доведення спростив Фелікс Клейн в 1894 р. Його доведення додано до роботи «Питання елементарної і вищої математики», ч. 1, що вийшла в Геттінгені в 1908 р.

Оскільки в Евклідовій геометрії площа круга і довжина кола є функціями числа π, то доведення трансцендентності π поклало край суперечці про квадратуру круга, що тривала понад 2,5 тисячі років.

Досі невідомо, чи є π нормальним числом.

Співвідношення

Відомо багато формул з числом $\pi$ :

Франсуа Вієт, 1593:

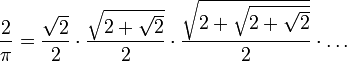
$\frac2\pi= \frac{\sqrt{2}}2\cdot \frac{\sqrt{2+\sqrt2}}2\cdot \frac{\sqrt{2+\sqrt{2+\sqrt2}}}2 \cdot \ldots$

Формула Валліса:

$\frac{2}{1} \cdot \frac{2}{3} \cdot \frac{4}{3} \cdot \frac{4}{5} \cdot \frac{6}{5} \cdot \frac{6}{7} \cdot \frac{8}{7} \cdot \frac{8}{9} \cdots = \frac{\pi}{2}$

Ряд Лейбніца:

$\frac{1}{1} - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \frac{1}{9} - \cdots = \frac{\pi}{4}$

Формула Г. В. Лейбніца

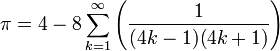
$\pi=4-8\sum_{k=1}^{\infty} \left ( \frac{1}{(4k-1)(4k+1)} \right )$

Тотожність Ейлера:

$e^{\pi i} + 1 = 0\;$

Так званий «інтеграл Пуассона» або «інтеграл Ґаусса»

$\int_{-\infty}^{\infty}\ e^{-x^2}{dx} = \sqrt{\pi}$

Історія розрахунків

Античність

Найперші відомі записані свідчення наближень числа $\pi$ датуються близько 1900 року до.н. е.; це 256/81 ≈ 3.160 (Єгипет) і 25/8 = 3.125 (Вавилон), обидва в межах 1 процента від дійсного значення. Індійський текст Шатапатха-Брахмана дає значення $\pi$ як 339/108 ≈ 3.139. Вважається, що параграф із Царів 7:23 і Хронік 4:2 в якому розглядається церемоніальний басейн в церкві Царя Соломона з діаметром в десять ліктів і периметром тридцять ліктів, показує, що автори вважали $\pi$ близьким в значенні до трьох, що різні вчені намагались пояснити через різні припущення такі як шестикутний басейн або вигнутий назовні обідок.

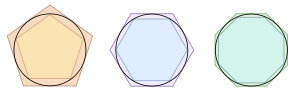
Діаграми обчислення числа пі Архімедом

Архімед (287—212 до н.е), можливо, першим запропонував метод обчислення $\pi$ математичним способом. Для цього він вписував у коло і описував біля нього правильні багатокутники. Приймаючи діаметр кола за одиницю, Архімед розглядав периметр вписаного багатокутника як нижню оцінку довжини кола, а периметр описаного багатокутника як верхню оцінку. Таким чином, для шестикутника виходить $3 < \pi < 2\sqrt{3}$ .

Розглядаючи правильний 96-кутник, Архімед отримав оцінку $3+\frac{10}{71} < \pi <3+\frac{1}{7}$ .

Птоломей в своєму Альмагесті дає значення 3.1416, яке він міг отримати в Аполлонія з Перги. Близько 265 року н. е. математик Лю Хуей знайшов простий і точний спосіб ітераційного алгоритму розрахунку числа $\pi$ з будь-якою точністю. Він особисто довів розрахунок до 3072-кутника і отримав наближене значення $\pi$ ≈ 3.1416. Пізніше Лю Хуєй винайшов швидкий спосіб розрахунку $\pi$ і отримав наближене значення 3.14, провівши розрахунок тільки для 96-кутника та скористався з того факту, що різниця в площі між серією багатокутників утворюють геометричну прогресію кратну 4. Близько 480 року китайський математик Цу Чунчжі продемонстрував. що $\pi$ ≈ 355/113 (≈ 3.1415929), і показав що 3.1415926 < $\pi$ < 3.1415927, використавши алгоритм Лю Хуєйя довів розрахунок до 12288-кутника. Це значення залишалось найточнішим наближенням $\pi$ протягом 900 років. В Індії Аріабхата і Бхаскара використовували наближення 62832/20000 = 3,1416.

Друге тисячоліття нашої ери

До другого тисячоліття н. е. число $\pi$ було розраховане з точністю не більшою ніж 10 цифр в записі числа. Наступний великий поступ у вивченні числа $\pi$ прийшов з розвитком нескінченних рядів і, відповідно, з відкриттям математичного аналізу, що дозволило розраховувати $\pi$ з будь-якою бажаною точністю розглядаючи необхідну кількість членів такого ряду. Близько 1400 року Мадхава Сангамаграма знайшов перший з таких рядів:

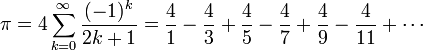
${\pi} = 4\sum^\infty_{k=0} \frac{(-1)^k}{2k+1} = \frac{4}{1} - \frac{4}{3} + \frac{4}{5} - \frac{4}{7} + \frac{4}{9} - \frac{4}{11} + \cdots\!$

Зараз цей ряд відомий як ряд Мадхави-Лейбніца або ряд Грегорі-Лейбніца оскільки його знову відкрили Джеймс Грегорі та Готфрід Лейбніц у 17-тому столітті. Проте, швидкість сходження занадто повільна, щоб розрахувати багато значущих цифр на практиці; треба додати близько 4000 членів ряду, щоб вдосконалити наближення Архімеда. Проте, перетворивши ряд у такий вигляд

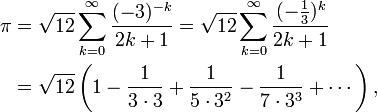
$\begin{align} \pi &= \sqrt{12}\sum^\infty_{k=0} \frac{(-3)^{-k}}{2k+1} = \sqrt{12}\sum^\infty_{k=0} \frac{(-\frac{1}{3})^k}{2k+1} \\ &= \sqrt{12}\left(1-{1\over 3\cdot3}+{1\over5\cdot 3^2}-{1\over7\cdot 3^3}+\cdots\right), \end{align}$

Мадхава зміг розрахувати $\pi$ як 3.14159265359, що правильно з точністю до 11 десяткових цифр. Цей рекорд побив Перський математик Джамшид ал-Каши, який розрахував $\pi$ з точністю до 16 десяткових цифр. Перший значний європейський внесок з часів Архімеда зробив німецький математик Лудольф ван Цейлен (1536—1610). Він витратив десять років на обчислення числа $\pi$ з 20-ма десятковими цифрами (цей результат був опублікований у 1596 році). Застосувавши метод Архімеда, він довів подвоєння до n-кутника, де n=60·2²⁹. Виклавши свої результати в творі «Про коло» («Van den Cirkel»), Лудольф закінчив його словами: «У кого є бажання, хай йде далі». Після смерті в його рукописах було виявлено ще 15 точних цифр числа $\pi$ . Лудольф заповів, щоб знайдені ним знаки були висічені на його надгробному камені. На честь його число $\pi$ іноді називали «лудольфовим числом».

Приблизно в той самий час в Європі з'явились методи розрахунку нескінченних рядів та добутків. Першим таким представленням була формула Вієта:

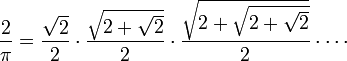
$\frac2\pi = \frac{\sqrt2}2 \cdot \frac{\sqrt{2+\sqrt2}}2 \cdot \frac{\sqrt{2+\sqrt{2+\sqrt2}}}2 \cdot \cdots\!$

яку знайшов Франсуа Вієт в 1593 році. Інший відомий результат — це формула Валліса:

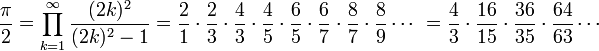
$\frac{\pi}{2} = \prod^\infty_{k=1} \frac{(2k)^2}{(2k)^2-1} = \frac{2}{1} \cdot \frac{2}{3} \cdot \frac{4}{3} \cdot \frac{4}{5} \cdot \frac{6}{5} \cdot \frac{6}{7} \cdot \frac{8}{7} \cdot \frac{8}{9} \cdots\ = \frac{4}{3} \cdot \frac{16}{15} \cdot \frac{36}{35} \cdot \frac{64}{63} \cdots\!$

знайдена Джоном Валлісом в 1655.

Ісаак Ньютон вивів arcsin ряд для $\pi$ в 1665-66 і розрахував 15 цифр:

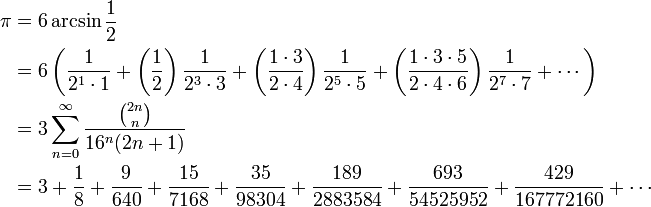
$\begin{align} \pi &= 6 \arcsin \frac {1} {2} \\ & = 6 \left( \frac {1} {2^1 \cdot 1} + \left( \frac {1} {2} \right) \frac {1} {2^3 \cdot 3} + \left( \frac {1 \cdot 3} {2 \cdot 4} \right) \frac {1} {2^5 \cdot 5} + \left( \frac{1 \cdot 3 \cdot 5} {2 \cdot 4 \cdot 6 } \right) \frac{1} {2^7 \cdot 7} + \cdots \right) \\ &= 3 \sum_{n=0}^\infty \frac {\binom {2n} n} {16^n(2n+1)} \\ & = 3 + \frac{1}{8} + \frac{9}{640} + \frac{15}{7168} + \frac{35}{98304} + \frac{189}{2883584} + \frac{693}{54525952} + \frac{429}{167772160} + \cdots \end{align}$

хоча він пізніше визнав: «Мені соромно казати як багато разів я виконав ці розрахунки, не робив ніяких інших справ увесь цей час». Він сходиться лінійно до $\pi$ з швидкістю сходження μ, яка додає щонайменше три десяткові цифри за кожних 5 доданків. Коли n наближається до безкінечності, μ наближається 1/4 і 1/μ наближається до 4:

$\mu = \frac {(2n-1)^2} {8n(2n+1)}; \frac {1} {\mu} = \frac {8n(2n+1)} {(2n-1)^2}$ .

В 1706 Джон Мечин був першим, хто розрахував 100 десяткових цифр числа $\pi$ , використовуючи ряди arctan у формулі:

$\frac{\pi}{4} = 4\,\mathrm{arctg}\frac{1}{5} - \mathrm{arctg}\frac{1}{239}$

де

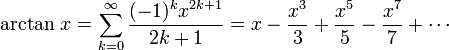
$\arctan \, x = \sum^\infty_{k=0} \frac{(-1)^k x^{2k+1}}{2k+1} = x - \frac{x^3}{3} + \frac{x^5}{5} - \frac{x^7}{7} + \cdots\!$

Розклавши арктангенс у ряд Тейлора, можна отримати ряд, що швидко збігається і придатний для обчислення числа $\pi$ з більшою точністю. Ейлер, автор позначення $\pi$ , отримав 153 вірних знаки. У 1777 році Бюффон запропонував статистичний метод обчислення числа пі, відомий як приклад Бюффона.

У 1873 році англієць В. Шенкс, після 15 років праці, обчислив 707 знаків; щоправда, через помилку тільки перші 527 з них були правильними. Щоб запобігти подібних помилок, сучасні обрахування такого роду здійснюються двічі. Якщо результати збігаються, то вони зі значною ймовірністю правильні. Помилку Шенкса було виявлено у 1948 році одним із перших комп'ютерів, ним же за декілька годин було вирахувано 808 знаків $\pi$ .

Теоретичні досягнення в 18-му століття привели до осягнення природи числа $\pi$ , чого не вдалось би досягнути тільки самими числовими розрахунками. Йоганн Генріх Ламберт довів ірраціональність $\pi$ 1761 року, а Адрієн-Марі Лежандр 1774 року довів ірраціональність $\pi$ ². Тоді як Леонард Ейлер 1735 року розв'язав знамениту Базельську задачу і в результаті знайшов точне значення Ріманової дзета-функції для числа 2.

$\zeta(2)=\sum^\infty_{k=1} \frac{1}{k^2} = \frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \cdots\!$

що дорівнює $\pi$ ²/6, таким чином він встановив глибокий зв'язок між $\pi$ та простими числами. Обоє Лежандр та Ейлер припускали, що число $\pi$ може бути трансцендентне, що зрештою і довів Фердинанд фон Ліндеман 1882 року.

Обчислення в епоху комп'ютерів

Практично, фізикам потрібно тільки 39 цифр числа $\pi$ , щоб зробити коло розміром як видимий всесвіт з точністю до розміру атома водню. Настанням епохи цифрових комп'ютерів в 20-му столітті призвело до зростання кількості нових рекордів в розрахунку числа $\pi$ . Джон фон Нейман та його команда використали ENIAC щоб розрахувати 2037 цифр числа $\pi$ 1949 року, цей розрахунок тривав 70 годин. Додаткові тисячі десяткових розрядів отримали в наступні десятиріччя, а рубіж в мільйон цифр перетнули в 1973 році. Прогрес був спричинений не тільки швидшими комп'ютерами, але й новими алгоритмами. Один з найзначніших проривів було відкриття швидкого перетворення Фур'є в 1960-х, що дало можливість комп'ютерам робити швидко арифметичні дії з надзвичайно великими числами.

На початку 20-го століття індійський математик Срініваса Рамануджан відкрив багато нових формул для числа $\pi$ , деякі з них стали знамениті через свою елегантність та математичну глибину. Обчислювальні алгоритми, засновані на формулах Рамануджана працюють дуже швидко. Одна з цих формул:

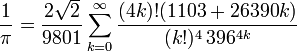
$\frac{1}{\pi} = \frac{2\sqrt{2}}{9801} \sum^\infty_{k=0} \frac{(4k)!(1103+26390k)}{(k!)^4 \, 396^{4k}}$

де k! — це факторіал k

А ось також підбірка інших формул:

$\pi=\frac{1}{Z}\!$	$Z=\sum_{n=0}^{\infty } \frac{((2n)!)^3(42n+5)} {(n!)^6{16}^{3n+1}}\!$
$\pi=\frac{4}{Z}\!$	$Z=\sum_{n=0}^{\infty } \frac{(-1)^n(4n)!(21460n+1123)} {(n!)^4{441}^{2n+1}{2}^{10n+1}}$
$\pi=\frac{4}{Z}\!$	$Z=\sum_{n=0}^{\infty } \frac{(6n+1)\left ( \frac{1}{2} \right )^3_n} {{4^n}(n!)^3}\!$
$\pi=\frac{32}{Z}\!$	$Z=\sum_{n=0}^{\infty } \left (\frac{\sqrt{5}-1}{2} \right )^{8n} \frac{(42n\sqrt{5} +30n + 5\sqrt{5}-1) \left ( \frac{1}{2} \right )^3_n} {{64^n}(n!)^3}\!$
$\pi=\frac{27}{4Z}\!$	$Z=\sum_{n=0}^{\infty } \left (\frac{2}{27} \right )^n \frac{(15n+2)\left ( \frac{1}{2} \right )_n \left ( \frac{1}{3} \right )_n \left ( \frac{2}{3} \right )_n} {(n!)^3}\!$
$\pi=\frac{15\sqrt{3}}{2Z}\!$	$Z=\sum_{n=0}^{\infty } \left ( \frac{4}{125} \right )^n \frac{(33n+4)\left ( \frac{1}{2} \right )_n \left ( \frac{1}{3} \right )_n \left ( \frac{2}{3} \right )_n} {(n!)^3}\!$
$\pi=\frac{85\sqrt{85}}{18\sqrt{3}Z}\!$	$Z=\sum_{n=0}^{\infty } \left ( \frac{4}{85} \right )^n \frac{(133n+8)\left ( \frac{1}{2} \right )_n \left ( \frac{1}{6} \right )_n \left ( \frac{5}{6} \right )_n} {(n!)^3}\!$
$\pi=\frac{5\sqrt{5}}{2\sqrt{3}Z} \!$	$Z=\sum_{n=0}^{\infty } \left ( \frac{4}{125} \right )^n \frac{(11n+1)\left ( \frac{1}{2} \right )_n \left ( \frac{1}{6} \right )_n \left ( \frac{5}{6} \right )_n} {(n!)^3}\!$
$\pi=\frac{2\sqrt{3}}{Z} \!$	$Z=\sum_{n=0}^{\infty } \frac{(8n+1)\left ( \frac{1}{2} \right )_n \left ( \frac{1}{4} \right )_n \left ( \frac{3}{4} \right )_n} {(n!)^3{9}^{n}}\!$
$\pi=\frac{\sqrt{3}}{9Z} \!$	$Z=\sum_{n=0}^{\infty } \frac{(40n+3)\left ( \frac{1}{2} \right )_n \left ( \frac{1}{4} \right )_n \left ( \frac{3}{4} \right )_n} {(n!)^3{49}^{2n+1}}\!$
$\pi=\frac{2\sqrt{11}}{11Z} \!$	$Z=\sum_{n=0}^{\infty } \frac{(280n+19)\left ( \frac{1}{2} \right )_n \left ( \frac{1}{4} \right )_n \left ( \frac{3}{4} \right )_n} {(n!)^3{99}^{2n+1}}\!$
$\pi=\frac{\sqrt{2}}{4Z} \!$	$Z=\sum_{n=0}^{\infty } \frac{(10n+1) \left ( \frac{1}{2} \right )_n \left ( \frac{1}{4} \right )_n \left ( \frac{3}{4} \right )_n} {(n!)^3{9}^{2n+1}}\!$
$\pi=\frac{4\sqrt{5}}{5Z} \!$	$Z=\sum_{n=0}^{\infty } \frac{(644n+41) \left ( \frac{1}{2} \right )_n \left ( \frac{1}{4} \right )_n \left ( \frac{3}{4} \right )_n} {(n!)^35^n{72}^{2n+1}}\!$
$\pi=\frac{4\sqrt{3}}{3Z} \!$	$Z=\sum_{n=0}^{\infty } \frac{(-1)^n(28n+3) \left ( \frac{1}{2} \right )_n \left ( \frac{1}{4} \right )_n \left ( \frac{3}{4} \right )_n} { (n!)^3{3^n}{4}^{n+1}}\!$
$\pi=\frac{4}{Z}\!$	$Z=\sum_{n=0}^{\infty } \frac{(-1)^n(20n+3) \left ( \frac{1}{2} \right )_n \left ( \frac{1}{4} \right )_n \left ( \frac{3}{4} \right )_n} { (n!)^3{2}^{2n+1}}\!$
$\pi=\frac{72}{Z} \!$	$Z=\sum_{n=0}^{\infty } \frac{(-1)^n(4n)!(260n+23)}{(n!)^44^{4n}18^{2n}}\!$
$\pi=\frac{3528}{Z} \!$	$Z=\sum_{n=0}^{\infty } \frac{(-1)^n(4n)!(21460n+1123)}{(n!)^44^{4n}882^{2n}}\!$

де

$(x)_n \!$

це символ Покхемера для спадного факторіала.

Пов'язану формулу відкрили брати Чудновскі 1987 року:

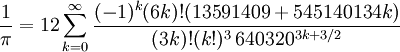$\frac{1}{\pi} = 12 \sum^\infty_{k=0} \frac{(-1)^k (6k)! (13591409 + 545140134k)}{(3k)!(k!)^3 \, 640320^{3k + 3/2}}$ ,

який дає 14 цифр за один член ряду. Чудновскі використали цю формулу, щоб встановити кілька рекордів з обчислення числа $\pi$ в кінці 1980-х, включно з першим обчисленням понад 1 мільярд (1,011,196,691) знаків 1989 року. Ця формула залишається добрим вибором для розрахунку $\pi$ на програмах, що працюють на персональному комп'ютері, на противагу суперкомп'ютерам, які використовують для встановлення сучасних рекордів.

Тоді як ряди зазвичай підвищують точність на певну кількість розрядів за кожен член ряду, існують також алгоритми, що багатократно збільшують кількість правильних цифр за кожен підхід, з тим недоліком, що кожен крок вимагає значної кількості обчислювальних ресурсів. Прорив був зроблений 1975 року, коли Річард Брент та Юджин Саламін незалежно один від одного відкрили алгоритм Брента-Саламіна, в якому використовуються тільки арифметичні дії для подвоєння кількості правильних цифр за кожен крок. На початковому етапі алгоритму встановимо такі вихідні значення:

$a_0 = 1 \quad \quad \quad b_0 = \frac{1}{\sqrt 2} \quad \quad \quad t_0 = \frac{1}{4} \quad \quad \quad p_0 = 1\!$

і проводимо ітерації

$a_{n+1} = \frac{a_n+b_n}{2} \quad \quad \quad b_{n+1} = \sqrt{a_n b_n}\!$

$t_{n+1} = t_n - p_n (a_n-a_{n+1})^2 \quad \quad \quad p_{n+1} = 2 p_n\!$

до тих пір, поки a_n і b_n не стануть достатньо близькі. Тоді оцінка значення $\pi$ проводиться за формулою:

$\pi \approx \frac{(a_n + b_n)^2}{4 t_n}.\!$

Працюючи за цією схемою, достатньо зробити 25 ітерацій, щоб досягти точності 45 мільйонів правильних знаків. Схожий алгоритм, що вчетверо збільшує точність за кожен крок, знайшли Джонатан та Пітер Боруейни. Цей метод використовували Ясумаса Канада та його команда, щоб встановити більшість рекордів з розрахунку числа $\pi$ , починаючи з 1980 року аж до розрахунку 206,158,430,000 десяткових знаків числа п 1999 року. У 2002 році Канада та його група встановили новий рекорд — 1,241,100,000,000. Хоча більшість попередніх рекордів були встановлені за допомогою алгоритму Брента-Саламіна, при розрахунках 2002 року використовували формули тупу Мечиновських, які хоч і потребували більше ітерацій, зате радикально знижували використання пам'яті. Розрахунки робили на суперкомп'ютері Hitachi з 64 вузлів та з 1 терабайтом оперативної пам'яті, який був здатний виконувати 2 трильйони операцій в секунду.

У 1997 році Дейвід Х. Бейлі, Пітер Боруейн і Саймон Плафф винайшли спосіб швидкого обчислення довільної двійкової цифри числа $\pi$ без обчислення попередніх цифр, заснований на формулі

$\pi = \sum_{i=0}^{\infty}\frac{1}{16^i}\left(\frac{4}{8i+1}-\frac{2}{8i+4}-\frac{1}{8i+5}-\frac{1}{8i+6}\right)$

В січні 2010 року рекорд був майже 2.7 трильйонів знаків, його встановив французький програміст Фабріс Беллар на персональному комп'ютері Це побило попередній рекорд 2,576,980,370,000 знаків, що встановив Дайзуке Такахаші на T2K-Tsukuba System, суперкомп’ютер університету Цукуба, що в Токіо 6 серпня 2010 року в PhysOrg.com опубліковано новину, що японський та американський комп'ютерні фахівці Шигеру Кондо та Олександр Йі заявили, що вони розрахували значення $\pi$ до 5 трильйонів знаків на персональному комп'ютері, подвоївши попередній рекорд. Послідовність цифр у числі Пі, давно хвилювала математиків своєю непередбачуваністю,і вона є дійсно випадковою.
Вчені Токійського університету зуміли поставити новий світовий рекорд в обчисленнях «числа Пі». Відому математичну константу вони порахували до 12411-трильйонного знака. Для цього групі програмістів і математиків, яку очолював професор Ясумаса Канада, знадобилася спеціальна програма, суперкомп`ютер і 400 годин машинного часу, повідомляє Associated Press.
Новий рекорд буде внесено до Книги рекордів Гіннеса. Попереднє рекордне досягнення було поставлено вченими з Канади, які змогли порахувати «число Пі» з точністю 206158 млрд знаків після коми. Японці ж в свою чергу змогли перерахувати «число Пі» у 60,2014 рази більш точно.
Найбільш складним етапом у встановленні нового рекорду стала комп`ютерна програма, яка виконує операцію обчислення «числа Пі», - на її написання та налагодження пішло більше 5 років. Саме ж обчислення відняло менше місяця і переслідувало до того ж суто практичну мету протестувати новий суперкомп`ютер Hitachi, здатний виконувати два трильйона операцій на секунду.

Подання у вигляді ланцюгового дробу

Послідовність з часткових знаменників простого ланцюгового дробу для $\pi$ не дає ніякої очевидної схеми

$\pi=[3;7,15,1,292,1,1,1,2,1,3,1,14,2,1,1,2,2,2,2,1,84,\cdots]$

чи

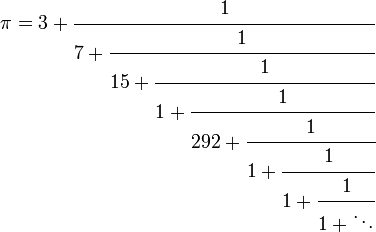
$\pi=3+\textstyle \cfrac{1}{7+\textstyle \cfrac{1}{15+\textstyle \cfrac{1}{1+\textstyle \cfrac{1}{292+\textstyle \cfrac{1}{1+\textstyle \cfrac{1}{1+\textstyle \cfrac{1}{1+\ddots}}}}}}}$

Проте якщо використовувати узагальнені ланцюгові дроби то отримаємо певні закономірності:

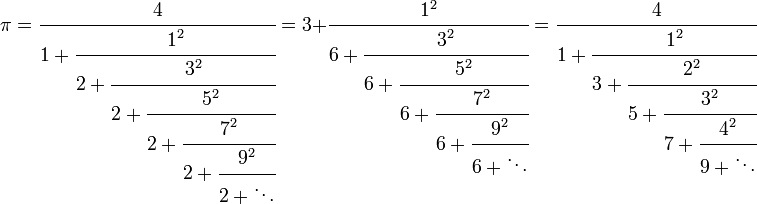
$\pi=\textstyle \cfrac{4}{1+\textstyle \cfrac{1^2}{2+\textstyle \cfrac{3^2}{2+\textstyle \cfrac{5^2}{2+\textstyle \cfrac{7^2}{2+\textstyle \cfrac{9^2}{2+\ddots}}}}}} =3+\textstyle \cfrac{1^2}{6+\textstyle \cfrac{3^2}{6+\textstyle \cfrac{5^2}{6+\textstyle \cfrac{7^2}{6+\textstyle \cfrac{9^2}{6+\ddots}}}}} =\textstyle \cfrac{4}{1+\textstyle \cfrac{1^2}{3+\textstyle \cfrac{2^2}{5+\textstyle \cfrac{3^2}{7+\textstyle \cfrac{4^2}{9+\ddots}}}}}$

Наближення

Наближене значення з точністю до 1000 десяткових знаків:

3,14159 26535 89793 23846 26433 83279 50288 41971 69399 37510

58209 74944 59230 78164 06286 20899 86280 34825 34211 70679

82148 08651 32823 06647 09384 46095 50582 23172 53594 08128

48111 74502 84102 70193 85211 05559 64462 29489 54930 38196

44288 10975 66593 34461 28475 64823 37867 83165 27120 19091

45648 56692 34603 48610 45432 66482 13393 60726 02491 41273

72458 70066 06315 58817 48815 20920 96282 92540 91715 36436

78925 90360 01133 05305 48820 46652 13841 46951 94151 16094

33057 27036 57595 91953 09218 61173 81932 61179 31051 18548

07446 23799 62749 56735 18857 52724 89122 79381 83011 94912

98336 73362 44065 66430 86021 39494 63952 24737 19070 21798

60943 70277 05392 17176 29317 67523 84674 81846 76694 05132

00056 81271 45263 56082 77857 71342 75778 96091 73637 17872

14684 40901 22495 34301 46549 58537 10507 92279 68925 89235

42019 95611 21290 21960 86403 44181 59813 62977 47713 09960

51870 72113 49999 99837 29780 49951 05973 17328 16096 31859

50244 59455 34690 83026 42522 30825 33446 85035 26193 11881

71010 00313 78387 52886 58753 32083 81420 61717 76691 47303

59825 34904 28755 46873 11595 62863 88235 37875 93751 95778

18577 80532 17122 68066 13001 92787 66111 95909 21642 01989…

Застосування числа Пі

             В рамках своєї роботи науковці використовували спеціально створений для обчислення фундаментальної константи комп’ютер, який працював на протязі 371 дня. Десятитрилльйонна цифра числа Пі дорівнює п’яти.
Безумовно, на практиці знання такої кількості цифр не потрібне. Так, наприклад, всього 39 знаків числа ПІ достатньо для того, щоб обчислити окружність з діаметром, рівним діаметру Всесвіту, з похибкою менше діаметра одного атома водню.
      Крім того, з цифрами цієї математичної константи безпосередньо пов’язана велика кількість теоретичних питань, для яких подібного роду дослідження – фактично експериментальна перевірка гіпотез.
        Наприкінці березня поточного року музикант з Сполучених Штатів на ім’я Майкл Блейк поклав число ПІ на музику. Для цього він взяв 31 цифру після знаку коми, поставив кожну з них у відповідність до ноти. З тієї причини, що існує 7 нот, а цифр 10, йому довелося так би мовити «забратися» в сусідню октаву.Використовуючи так зване «квінтове коло», музикант поставив цифрами відповідні акорди. Потім, за допомогою використання отриманих даних, Майкл аранжував мелодію в темпі 157 ударів в хвилину, тобто 314, поділено на 2.

За словами математиків, доказ того, що Пі - випадкове і ніколи не повторює саме себе, потрібно аж ніяк не як черговий кумедний математичний курйоз: це важливе наукове досягнення, на якому можуть бути засновані такі суто практичні речі, як, наприклад, створення шифрів, що не розшифровуються. .
Серед всіх міркувань та роздумів про те, що в числі Пі закодована будь-яка обрана нами книга, у тому ж числі і Старий Заповіт ... і раптом дізнаємося, що в Торі уже є число Пі з точністю до п`ятого знака після коми Раніше в слов`янських мовах букви використовувалися в якості цифр. В івриті літери використовують як цифри і числа і по сьогоднішній день, паралельно зі звичною нам арабської символікою. Більше того, часто підрахунок числового значення слів використовується при дослідженні Тори, це - так звана гематрія. Числове значення слова "кав" = (КОФ: 100 + вав: 6) = 106, "кав`е" = (КОФ: 100 + вав: 6 + hей: 5) = 111. Для отримання поправочного коефіцієнта з відмінностей у написанні і вимові, що був збережений для нас через тисячоліття, ділимо 111 на 106.
Множимо наш «грубий» показник 3 = (30/10) співвідношення числа ліктів на поправку: 3 * (111/106) = 3,14159 ...

День Пі

День пі — свято було засновано у 1987 році фізиком з Сан-Франциско Ларрі Шоу, який помітив, що в американській системі запису дат (місяць / число) дата 14 березня - 3 / 14 - і час 1.59 збігається з першими розрядами числа π = 3, 14159.С тих пір кожен рік люди не байдужі до математики відзначають День числа Пі.
У цей день прийнято читати хвалебні промови на честь числа Пі, його ролі в житті людства, активісти малюють анти утопічні картини світу без Пі, печуть і їдять пі-ріг із зображенням грецької букви Пі або з першими цифрами самого числа, п`ють напої і грають в ігри, що починаються на пі, вирішують математичні головоломки і загадки тощо.
Окрім того, цей день (14 березня) є також і днем народження Альберта Енштейна, що надає йому додаткової значущості в очах математиків.

Святкування Міжнародної дня числа Пі проходять і в Україні. Зокрема сьогодні в Сімферополі наукова бібліотека імені Івана Франка та арт-група Хаос представляють проект Інша реальність. "Центральна частина проекту - картина Хаос, мозаїка 3 метри на 3 метри, створена на основі 100 000 знаків числа ПІ після коми", - повідомляють організатори проекту.

Приблизний День пі є однією з двох дат: або 22 липня (записується 22/7 - цей дріб дорівнює 3.14, що є приблизним виразом π), або 26 квітня (25 квітня високосного року) - день, коли Земля проходить дві астрономічні одиниці по своїй орбіті з початку календарного року: в цей день загальна довжина орбіти Землі, поділена на довжину вже пройденої ділянки, дорівнює π (тобто Земля пройшла в цей момент по своїй орбіті 2 радіани).

Цікаві факти про число пі

Дивний марафон, розпочатий Архімедом, сьогодні так само далекий від завершення, як і дві тисячі років назад. У Книгу рекордів Гіннеса потрапив результат професора Григорія Чудновського із США, до речі, випускника Київського університету. Йому першому в світі вдалося перевершити рубіж в мільярд знаків! Проте рекорд протримався недовго, і співробітники Токійського університету Я.Канада і Д.Такахаші підняли планку до висоти — 206 мільярдів знаків. Але виявилось, що і це - ще не межа. 2 серпня 2010 року американський студент Олександр Йі і японський дослідник Сігеру Кондо знайшли 5 трильйонів цифр, а приблизно через рік, 19 жовтня 2011 року вони ж поліпшили свій результат – знайшли 10 трильйонів цифр числа пі.
Чи зупиниться коли-небудь ця дивна гонитва за зникаючими в нескінченності знаками числа «пі»? Мабуть, це питання можна переформулювати так: чи припинить будь-коли своє існування людська цивілізація?
Пів життя Вільям Шенкс вираховував 707 цифр, однак виявилось, що останні 180 знаків у «хвості» виявились неправильними.
Щороку у Всесвітній день числа «пі» фанати легендарного числа збираються в Інтернеті. Будь-який житель планети має змогу прийняти учать у глобальному проект «Pi-Hex». І це не проста забавка для комп’ютерних гурманів, а досить серйозний науковий проект.
π = 3.1415926535 8979323846 2643383279 5028841971 6939937510
5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196 4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273 7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094 3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912 9833673362 4406566430 8602139494 6395224737 1907021798 6094370277 0539217176 2931767523 8467481846 7669405132 0005681271 4526356082 7785771342 7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235 4201995611 2129021960 8640344181 5981362977 4771309960 5187072113 4999999837 2978049951 0597317328 1609631859 5024459455 3469083026 4252230825 3344685035 2619311881 7101000313 7838752886 5875332083 8142061717 7669147303 5982534904 2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787 6611195909 2164201989 ...
Неофіційне свято “День числа Пі” відзначається 14 березня, яке в американському форматі дат (місяць/день) записують як 3.14, що відповідає наближеному значенню числа π. Вважається, що свято придумав 1987 року фізик із Сан-Франциско Ларрі Шоу. Він звернув увагу на те, що 14 березня рівно в 1:59 дата і час збігаються з першими розрядами числа Пі = 3,14159.
Ще однією датою, пов’язаною з числом π, є 22 липня, яке називають “Днем наближеного числа Пі” (Pi Approximation Day), оскільки в європейському форматі дат цей день записують як 22/7, а значення цього дробу є наближеним значенням числа π.
Світовий рекорд із запам’ятовування знаків числа π після коми належить китайцю Лю Чао, який 2006 року протягом 24 годин і 4 хвилин відтворив 67890 знаків після коми без жодної помилки. Того ж 2006 року японець Акіра Харагуті оголосив, що запам’ятав число Пі до 100-тисячного знака після коми, однак перевірити це офіційно не вдалося.
У штаті Індіана (США) 1897 року був випущений біль, який законодавчо встановив значення числа Пі рівним 3,2. Цей біль не став законом завдяки своєчасному втручанню професора математики, який брав участь у законодавчих зборах штату під час розгляду даного закону.
“Число для гренландських китів дорівнює трьом” написано в “Довіднику китобоя” 1960-х років випуску.
За станом на 2011 рік обчислено більше 10 трильйонів знаків після коми.
Створено художній фільм у жанрі психологічного трилеру, який названо на честь числа Пі (режисер і сценарист: Даррен Аронофскі, кінокомпанія Harvest Filmworks (США), тривалість 84 хв., дата виходу 12 липня 1998). Коротко про сюжет: геніальний математик і нумеролог Макс Коен вірить, що все на світі можна зрозуміти за допомогою чисел. Макс страждає від кластерного головного болю, параної та соціофобії. Єдиною людиною, з якою він спілкується, є його колишній вчитель Сол Роб Сон. На своєму комп'ютері “Евклід” Макс намагається зробити розрахунки, які б допомогли робити передбачення на біржі, але “Евклід” виходить із ладу, видавши послідовність з 216 цифр. Наступного ранку Макс перевіряє фінансові газети і з великим подивом розуміє, що його комп'ютер зробив абсолютно точне передбачення. Макс розповідає про це Солу, і той відповідає, що колись також натрапив на це число. У кав'ярні Макс зустрічає хасида Ленні, який захоплюється кабалою. Ленні розповідає Максу, що вірить, що в Торі зашифровано таємний код Бога. Потім Макс зустрічається з агентом Марсі Доусон з Уолл-стріт, який цікавиться його роботою та дає йому потужний мікропроцесор “Ming Mecca” в обмін на результати його досліджень. За допомогою нового процесора Макс аналізує Тору і знаходить те ж саме 216-значне число, за допомогою якого він передбачає будь-які події. Водночас його головний біль посилюється і стає нестерпним. Макс вирішує відмовитися від знання, яке шукав усе своє життя і прагне просто стати звичайною людиною.
Можливо, і Вавилонська башта звалилася не тому, що люди розгнівали Всевишнього, а тому, що розрахунки були неточні. Відомий римський архітектор Вітрувій, що жив в I столітті до н.е., використовував грубе наближення числа «пі», що привело до промахів в будівництві знаменитого Римського театру. Та і у наш час багато ультрасучасних конструкцій не витримують випробувань на міцність із-за «витівок» числа «пі». Наприклад, московський «Аквапарк» міг звалитися теж з цієї причини.
А в Книзі рекордів Гіннеса значиться ім`я 24-літнього китайського аспіранта Лу Чао, який визначив число Пі з точністю до 67890 знаків після коми за 24 години й 4 хвилини.
Коротке зведення рекордної гонитви за "хвостом" числа Пі виглядає так:
1995 - японець Хірюкі Гото зумів назвати по пам'яті 42 195 знаків після коми.
2004 - ще один представник Країни висхідного сонця, 59-річний Акіра Харагучі, підняв цю планку до 54-тисячних.
2005 - усе той же невгомонний Акіра Харагучі запам'ятав число Пі з точністю до 83 431 цифри після коми.
2005 - китаєць Чао Лю трохи не дотяг до рекорду свого східного сусіда : 67 890 знаків уміщалися в голові Лю.
«Парадокс числа пі» — жарт на тему математики, що мав місце в середовищі студентів до 80-х років (фактично, до масового поширення мікрокалькуляторів) і був пов'язаний з обмеженою точністю обчислень тригонометричних функцій і трансцендентних чисел. Суть полягає в наступній рівності: « 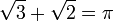$\sqrt{3}+\sqrt{2}=\pi$ ». Дійсно, в «докалькуляторну» епоху в розрахунках часто приймалися такі заокруглені значення: 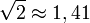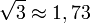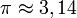$\sqrt{2}\approx1,41$ , $\sqrt{3}\approx1,73$ , $\pi\approx3,14$ , і рівність 1,73 + 1,41 = 3,14 здавалася правдивою. Першокурсникам часто пропонувалося довести зазначену рівність, наприклад методом Архімеда.Насправді зазначена рівність, звичайно ж, невірна — хоча б тому, що π — трансцендентне число, а ліворуч — алгебраїчне. Сума 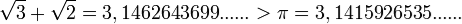$\sqrt{3}+\sqrt{2}=3,1462643699...... > \pi = 3,1415926535......$ вже при заокругленні до трьох знаків після коми.
Число пі, хоча й не є фізичною константою дуже часто фігурує у фізичних формулах, завдяки тому, що у них часто неявно закладені властивості кола, особливо у випадку симетрії, при якій зручно використовувати полярну, циліндричну або сферичну систему координат. Іншим джерелом появи числа пі у фізичних формулах є використання нормального розподілу:

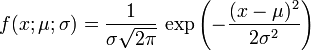$f(x;\mu;\sigma) = \frac{1}{\sigma\sqrt{2\pi}} \, \exp \left( -\frac{(x- \mu)^2}{2\sigma^2} \right)$ та перетворень Фур'є, заснованих на співвідношенні:

$\int_{-\infty}^\infty e^{i (\omega^\prime - \omega )t} dt = 2\pi \delta(\omega^\prime - \omega)$ ,де $\delta(x)$ - дельта-функція Дірака.

Досконалий День пі стався 14-го березня 1592 року в 6 годин, 53 хвилини та 58 секунд. Ця дата, записана в "американському" форматі виглядає як 3/14/1592 6:53:58, що відповідає першим 12-ти знакам в числі π: 3.14159265358. Але, зважаючи на те, що того часу ще не було впроваджено ніякого стандартизованого відліку часу, тим більше з потрібною точністю, скоріше за все цей момент ніким не святкувався.
Простий метод запам'ятати число $\pi$ з точністю до шести значущих цифр після коми:

випишемо парами перші три натуральних непарних числа: 113355.

розділимо список наполовину та поділимо друге число на перше: ${355 \over 113} = 3.141592 \ldots$

Що ж це за число таке, що вже майже п’ять тисячоліть примушує людей важко трудитися і витрачати життя для того, щоб додати до його «хвоста», чи запам’ятати зайву цифру?

3,14159 26535 89793 23846 26433 83279 50288 41971 69399 37510

58209 74944 59230 78164 06286 20899 86280 34825 34211 70679

82148 08651 32823 06647 09384 46095 50582 23172 53594 08128

48111 74502 84102 70193 85211 05559 64462 29489 54930 38196

44288 10975 66593 34461 28475 64823 37867 83165 27120 19091

45648 56692 34603 48610 45432 66482 13393 60726 02491 41273

72458 70066 06315 58817 48815 20920 96282 92540 91715 36436

78925 90360 01133 05305 48820 46652 13841 46951 94151 16094

33057 27036 57595 91953 09218 61173 81932 61179 31051 18548

07446 23799 62749 56735 18857 52724 89122 79381 83011 94912

98336 73362 44065 66430 86021 39494 63952 24737 19070 21798

60943 70277 05392 17176 29317 67523 84674 81846 76694 05132

00056 81271 45263 56082 77857 71342 75778 96091 73637 17872

14684 40901 22495 34301 46549 58537 10507 92279 68925 89235

42019 95611 21290 21960 86403 44181 59813 62977 47713 09960

51870 72113 49999 99837 29780 49951 05973 17328 16096 31859

50244 59455 34690 83026 42522 30825 33446 85035 26193 11881

71010 00313 78387 52886 58753 32083 81420 61717 76691 47303

59825 34904 28755 46873 11595 62863 88235 37875 93751 95778

18577 80532 17122 68066 13001 92787 66111 95909 21642 01989…

3,14159 26535 89793 23846 26433 83279 50288 41971 69399 37510

58209 74944 59230 78164 06286 20899 86280 34825 34211 70679

82148 08651 32823 06647 09384 46095 50582 23172 53594 08128

48111 74502 84102 70193 85211 05559 64462 29489 54930 38196

44288 10975 66593 34461 28475 64823 37867 83165 27120 19091

45648 56692 34603 48610 45432 66482 13393 60726 02491 41273

72458 70066 06315 58817 48815 20920 96282 92540 91715 36436

78925 90360 01133 05305 48820 46652 13841 46951 94151 16094

33057 27036 57595 91953 09218 61173 81932 61179 31051 18548

07446 23799 62749 56735 18857 52724 89122 79381 83011 94912

98336 73362 44065 66430 86021 39494 63952 24737 19070 21798

60943 70277 05392 17176 29317 67523 84674 81846 76694 05132

00056 81271 45263 56082 77857 71342 75778 96091 73637 17872

14684 40901 22495 34301 46549 58537 10507 92279 68925 89235

42019 95611 21290 21960 86403 44181 59813 62977 47713 09960

51870 72113 49999 99837 29780 49951 05973 17328 16096 31859

50244 59455 34690 83026 42522 30825 33446 85035 26193 11881

71010 00313 78387 52886 58753 32083 81420 61717 76691 47303

59825 34904 28755 46873 11595 62863 88235 37875 93751 95778

18577 80532 17122 68066 13001 92787 66111 95909 21642 01989…

doc

Завантажити

Зберегти на потім

Додав(-ла)

Демидюк Ганна Хомівна

Пов’язані теми

Математика, 9 клас, Методичні рекомендації

Додано

30 січня 2020

Переглядів

8807

Оцінка розробки

Відгуки відсутні