Методичний посібник "Параметри в тригонометрії"
У посібнику вміщено задачі із параметрами, які для більшості учнів традиційно є завданнями підвищеної складності. Розглядаються тригонометричні рівняння, нерівності та системи рівнянь. Приділено увагу питанням існування коренів рівняння, їх кількості на певному інтервалі. Представлено різні методи й підходи до вирішення завдань з метою найкращої підготовки учнів до ЗНО. Дана добірка матеріалу для самостійного рішення.
Призначено для вчителів математики, керівників гуртків, факультативів та учнів, які прагнуть розширити й поглибити свої знання з математики.
Зміст.
Введення………………………………………………………..5
§1. Тригонометричні рівняння з параметром
1.1 Розв’язування тригонометричних рівнянь…………..7
1.2 Умови існування рішень у рівняння………………..14
1.3 Кількість коренів рівняння…………………………..28
§2. Тригонометричні нерівності з параметрами…………….33
§3. Завдання підвищеної складності…………………...…….38
Список використаної літератури……………….…………….51
Введення.
У посібнику розглядаються розв’язування задач з параметрами, які для абсолютної більшості учнів традиційно є завданнями підвищеної труднощі. Завдання з параметрами відіграють важливу роль у формуванні логічного мислення й математичної культури у школярів, але їхнє рішення викликає у них значні труднощі. Це пов'язано з тим, що кожне рівняння чи нерівність з параметрами являє собою цілий клас звичайних рівнянь і нерівностей, для кожного з них має бути отримано рішення.
Посібник адресовано абітурієнтам, учням старших класів. Однак, починати знайомити учнів шкіл з подібними завданнями потрібно значно раніше - паралельно з відповідними розділами шкільної програми з математики. У запропонованому посібнику розглянуто задачі на рішення, з'ясування умов існування рішень, а також на визначення кількості рішень на певному інтервалі тригонометричних рівнянь, нерівностей і систем.
Мета даного посібника - створення умов для формування знань і умінь, необхідних для вирішення таких завдань, формування цілісного уявлення про методи їх розв’язування, розгляд різних типів завдань, підготовка учнів до випускних іспитів і зовнішнього незалежного оцінювання.
Представлено різні методи й підходи до вирішення завдань з метою найкращої підготовки учнів до ЗНО. Дана добірка матеріалу для самостійної підготовки.
Завдання, що містять параметри є свого роду критерієм засвоєння навчального матеріалу. У шкільному курсі алгебри і початків аналізу такі завдання розглядаються, але у вигляді окремої теми вони виділені тільки для профільних класів, тому у вчителів, які працюють із класами академічного рівня, найчастіше немає можливості приділити їм належної уваги, а учні, які хочуть і повинні знати даний матеріал, – є.
Вирішення представлених в посібнику завдань дозволяє:
- систематизувати та узагальнити раніше вивчений матеріал і розглянути його на більш високому рівні складності;
- вивчити методи і способи розв’язування різних типів завдань;
- формувати у школярів уміння застосовувати свої знання з різних розділів шкільного курсу математики для конструювання способу вирішення завдання в нестандартній ситуації;
- формувати дії самоконтролю у школярів;
- розвивати логічне мислення школярів;
- розвивати творчі здібності школярів при конструюванні способів вирішення завдань високого рівня складності;
- виховувати раціональність і креативність мислення учнів.
Посібник призначений для вчителів математики, керівників математичних гуртків, факультативів та для учнів, які прагнуть розширити й поглибити свої знання з математики.
§1. Тригонометричні рівняння з параметром.
1.1 РОЗВ’ЯЗУВАННЯ ТРИГОНОМЕТРИЧНИХ РІВНЯНЬ
Вирішити рівняння з параметрами - це означає, що для кожного допустимого значення параметра треба знайти всі рішення даного рівняння. Основний принцип рішення рівняння з параметром полягає в необхідності розгляду різних випадків залежно від значень параметра. Відповідь до рівняння з параметром записується у вигляді переліку проміжків зміни параметра із зазначенням для кожного проміжку рішень рівняння.
Приклад 1.1.01.![]()
Розв’язання.
-
Якщо
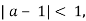
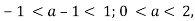
![]() , к
, к ![]()
2) ![]()
![]()
![]()
Якщо ![]()
![]()
![]()
Якщо ![]()
![]()
![]()
3) Якщо ![]() Рівняння розв’язків не має.
Рівняння розв’язків не має.
Відповідь: якщо ![]()
якщо![]()
якщо ![]()
![]()
якщо ![]() то розв’язків не має.
то розв’язків не має.
Приклад1.1.02. Розв’яжіть рівняння ![]()
![]()
Розв’язання.
Застосовуючи формулу різниці косинусів, одержимо![]()
![]()
![]()
Звідси ![]()
![]()
![]() .
.
![]() .
.
Друге рівняння має рішення, якщо ![]() , або
, або ![]() .
.
Відповідь. Якщо ![]()
![]() .
.
Якщо ![]()
Приклад 1.1.03. Розв’язати рівняння: ![]()
Розв’язання.
Так як ![]() то
то ![]()
![]()
Маємо два випадки.
1. При ![]()
2. При ![]() маємо рівняння
маємо рівняння![]()
![]() :
:
а![]() .
.
Так як рівняння має рішення, якщо ![]()
![]() то n може приймати значення
то n може приймати значення ![]()
Рішенням рівняння є ![]()
![]()
б) ![]()
Так як рівняння має рішення за умови, що
![]()
а ![]()
![]()
Відповідь: Якщо ![]()
якщо |![]()
![]()
![]() при
при ![]()
Приклад 1.1.04. Розв’язати рівняння: ![]()
Розв’язання.
Нехай ![]() тоді рівняння прийме вигляд
тоді рівняння прийме вигляд ![]()
Дискримінант рівняння: ![]()
Очевидно, що ![]() при
при ![]()
Якщо ![]()
Нехай ![]()
![]()
![]() або
або ![]() .
.
Так як ![]() то повинна виконуватись нерівність
то повинна виконуватись нерівність
![]()
Неважко помітити, що ![]()
З′ясуємо, при яких значеннях![]() виконується нерівність
виконується нерівність ![]()
Ця нерівність рівносильна системі ![]()
![]() Тоді
Тоді ![]()
![]()
![]()
Усі знайдені значення a належать проміжку![]() .
.
Отже, ![]() при
при ![]()
![]()
Відповідь.
Якщо ![]()
![]()
![]()
Якщо ![]()
![]()
Приклад 1.1.05. Розв’язати рівняння: ![]() .
.
Розв’язання.
Помноживши обидві частини рівняння на ![]() , отримаємо
, отримаємо ![]() .
.
Перетворюючи добуток синусів, матимемо
![]() ,
,
тобто ![]()
![]()
Звідки ![]()
![]()
![]()
![]()
Так як обидві частини рівняння помножили на ![]()
![]()
![]()
Ясно, що серії ![]()
![]()
спільних значень не мають.
Якщо ![]()
![]()
![]()
![]() . Зазначимо далі, що
. Зазначимо далі, що ![]() є розв’язком початкового рівняння лише при значенні
є розв’язком початкового рівняння лише при значенні ![]()
Це означає, що серія ![]() є розв’язком початкового рівняння лише при значеннях
є розв’язком початкового рівняння лише при значеннях
![]() .
.
Відповідь. Якщо ![]()
Якщо ![]()
![]()
Розв’яжіть самостійно.
Розв’яжіть рівняння для всіх значень параметра![]()
Відповідь: якщо ![]()
![]()
![]()
якщо ![]()
![]()
якщо ![]()
![]()
![]() якщо
якщо![]()
Відповідь: якщо ![]() то розв’язків немає;
то розв’язків немає;
якщо![]()
-
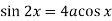 .
.
Відповідь: якщо ![]() то
то ![]() якщо
якщо![]()
![]()
Відповідь: якщо ![]()
![]()
якщо![]()
якщо ![]()
![]()
якщо ![]()
Відповідь: якщо | a | ≤ ![]() , то
, то
![]()
якщо | a | = ![]() , то х =
, то х = ![]() +πn, n
+πn, n ![]()
якщо a | > ![]() , то розв’язків немає.
, то розв’язків немає.
Відповідь: якщо ![]()
то розв’язків немає;
якщо ![]() то
то
![]()
якщо ![]() , то
, то
![]()
якщо ![]()
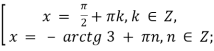
якщо ![]() , то
, то
![]()
-
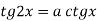
Відповідь: якщо ![]() ;
;
якщо ![]()
![]()
- Знайдіть усі значення параметру а, при яких система рівнянь
![]()
має розв’язки і розв’яжіть систему.
Відповідь: система має розв’язки тільки при а = 0.
x = ![]() +π(k +n), у =
+π(k +n), у = ![]() (k – n), n,k
(k – n), n,k ![]()
1.2. УМОВИ ІСНУВАННЯ РІШЕНЬ.
У цьому параграфі розглянуті рівняння, в яких треба встановити, при яких значеннях параметра а рівняння має рішення або не має їх.
Приклад 1.2.01. При якому значенні параметра а рівняння
![]() не має рішення.
не має рішення.
Розв’язання.
![]()
Нехай ![]() тоді
тоді ![]()
![]()
![]()
Отже, ![]() .
.
(Можна, записавши рівняння у вигляді
![]() і застосувавши теорему Вієта, отримати
і застосувавши теорему Вієта, отримати
![]()
Врахуємо, що ![]() Знаходимо, що рівняння
Знаходимо, що рівняння
![]() має корені за умови
має корені за умови
![]()
![]()
Рівняння ![]() має корені за умови
має корені за умови
![]()
![]()
Таким чином, наше рівняння має розв’язки, якщо
![]()
0 2 4 6 х
![]()
Тоді воно не має рішень, якщо ![]() .
.
Відповідь. ![]() .
.
Приклад 1.2.02. Знайдіть усі значення параметра ![]()
![]()
має рішення.
Розв’язання.
Введемо нову змінну:![]() , t∈[0;1]
, t∈[0;1]![]()
![]()
Щоб розв’язати квадратне рівняння зі змінною t, знайдемо його дискримінант:
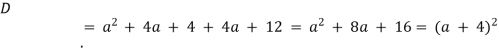
![]()
Тоді квадратне рівняння має рішення.
![]()
![]()
![]()
![]()
![]()
![]()
Число ![]()
![]() таким чином, задане нам тригонометричне рівняння з параметром має рішення за умови
таким чином, задане нам тригонометричне рівняння з параметром має рішення за умови
![]()
![]()
Відповідь. Рівняння має рішення при![]()
Приклад 1.2,03. При яких значеннях ![]()
![]() має рішення?
має рішення?
Розв’язання.
Застосовуючи формулу суми кубів, наведемо рівняння до виду
![]() ,
,
Вказуючи, що ![]() , отримуємо
, отримуємо
![]()
Замінюючи ![]()
![]() будемо мати
будемо мати
![]()
![]()
Так як ![]() то повинна виконуватись нерівність
то повинна виконуватись нерівність ![]() Звідси,
Звідси, ![]()
Відповідь. ![]()
Приклад1.2.04 (№35, ЗНО 2011). Знайдіть найменше значення ![]()
![]()
Розв’язання.
![]()
![]()
![]()
Якщо ![]() тоді
тоді ![]() .
.
![]()
![]()
![]()
Розв’яжемо кожну з нерівностей методом інтервалів:
![]()
![]() ;
;
![]()
![]()
 + + a
+ + a
![]()
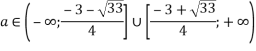
![]() ;
; ![]()
![]()
Маємо 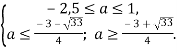
Порівняємо від’ємні та додатні корені квадратних тричленів:
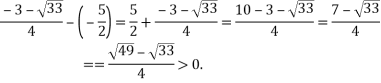
![]() .
.
![]()
Можемо розв’язати останню систему:

![]() 1 a
1 a
![]()
![]()
Отже, ![]() .
.
Найменше значення параметра a , що задовольняє умову задачі дорівнює ![]()
Відповідь.![]()
Приклад 1.2.05.Знайдіть НАЙМЕНШЕ значення параметра а, при якому має розв’язки рівняння:![]()
![]()
Розв’язання.
Оскільки ![]()
То рівняння набуває вигляду
![]() .
.
Враховуючи, що для будь-яких х виконується подвійна нерівність ![]()
Доходимо висновку, що подане рівняння матиме корені, якщо вираз ![]() набуватиме будь-якого значення з проміжку
набуватиме будь-якого значення з проміжку ![]() .
.
Розв’яжемо нерівність ![]() . Вона рівносильна системі
. Вона рівносильна системі
![]()
![]()
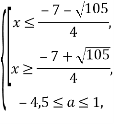
![]()
![]()
Найменшим з-поміж розв’язків є число -4,5.
Відповідь: -4,5.
Приклад 1.2.06 (№34 ЗНО 2014, додаткова сесія).
Знайдіть найбільше значення параметра a, при якому система рівнянь
![]()
має безліч розв’язків.
Розв’язання
Помножимо перше рівняння системи на ![]()
![]()
![]() рівняння перетворюється на неправильні рівності).
рівняння перетворюється на неправильні рівності).
З першого рівняння маємо: ![]() Щоб система мала безліч розв’язків здобуті значення
Щоб система мала безліч розв’язків здобуті значення ![]() мають задовольняти основну тригонометричну тотожність
мають задовольняти основну тригонометричну тотожність
![]() .
.
Отже,
![]()
звідки
![]()
Умову задачі задовольняє значення ![]()
Відповідь: 3.5.
Приклад 1.2.07. Знайдіть усі значення параметра ![]()
![]() не має коренів.
не має коренів.
Розв’язання.
![]()
![]()
![]()
![]()
![]()
Введемо нову змінну: ![]() ,
, ![]()
![]() .
.
Розглянемо функцію ![]() Треба дослідити її на найбільше і найменше значення на відрізку
Треба дослідити її на найбільше і найменше значення на відрізку ![]()
Знаходимо похідну![]()
Визначаємо критичні точки функції: ![]()
![]()
![]()
Число ![]() не належить проміжку
не належить проміжку![]()
![]()
![]() ;
;
![]()
![]()
Значить, при ![]() дане нам рівняння
дане нам рівняння ![]() не має коренів.
не має коренів.
Відповідь. Рівняння не має коренів
при р![]()
За даним завданням можуть бути задані наприклад такі питання:
1) При якому найбільшому цілому від'ємному значенні параметра р рівняння не має коренів?![]()
-
При якому найменшому натуральному значенні параметра р дане рівняння має корені?
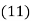
Приклад 1.2.08 . Знайдіть всі значення параметру р, при яких рівняння
![]() має розв’язки.
має розв’язки.
Розв’язання.
Область визначення для параметра р: ![]()
![]() Маємо
Маємо ![]()
Застосуємо метод допоміжного аргументу
![]()
![]()
Поділивши обидві частини рівняння на ![]() , отримаємо
, отримаємо
![]()
Зауважимо, при цьому у нас коефіцієнти перед синусом і косинусом володіють наступними властивостями:
![]()
![]()
![]()
![]()
![]()
Зауважимо, що невідому х шукати не треба![]()
![]() .
.
Тоді ![]() .
.
Враховуючи, що ця дріб приймає додатні значення, маємо ![]() .
.
Обидві частини нерівності теж беруть додатні значення. Отже, можна піднести обидві частини в квадрат.
![]() ;
;
![]()
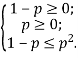
![]()
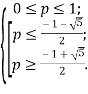 Отримаємо,
Отримаємо, ![]()
Відповідь:![]()
Приклад 1.2.09 Знайдіть значення параметру а , при яких рівняння ![]() має рішення.
має рішення.
Розв’язування.
![]() .
.
Поділимо частини рівняння на ![]() і отримуємо
і отримуємо
![]() .;
.;
![]() ;
;
Так як ![]() тоді позначимо
тоді позначимо
![]()
Тоді ![]() , де
, де ![]()
Відомо що ![]()
![]() ;
;
Якщо ![]() , тоді
, тоді ![]()
![]()
![]()
Відповідь:![]()
Приклад 1.2.10 Знайдіть значення параметру а , при яких рівняння
![]() має рішення.
має рішення.
Розв’язування.
![]()
![]()
![]()
![]()
![]() .
.
Якщо ![]() ,
,![]()
![]()
![]() . Наше рівняння приймає вид
. Наше рівняння приймає вид ![]() .
.
Розглянемо параболу ![]() .
.
![]() .
. ![]()
Тоді рівняння ![]() на відрізку
на відрізку ![]() може мати не більш одного кореня.
може мати не більш одного кореня. ![]() і
і ![]() мають різні знаки, отже
мають різні знаки, отже
![]()
![]()
![]()
![]()
Відповідь: ![]()
Приклад 1.2.11 Знайдіть значення параметру а , при яких рівняння
![]() має рішення.
має рішення.
Розв’язування.
![]() ;
;
![]() ;
;
Відомо,що ![]() Тоді
Тоді ![]() ;
;
Якщо ![]() ; то
; то ![]() ; Отже
; Отже ![]()
З другого рівняння ![]()
А перше рівняння виконується лише за умови:
![]()
![]()
![]()
Якщо ![]() , то
, то ![]() ;
;
![]()
![]()
Ця рівність неможлива, бо ![]()
![]()
Отже, і наше рівняння при жодному значенні параметру не має рішень.
Відповідь:![]()
Розв’яжіть самостійно.
Знайдіть усі значення параметру, при яких рівняннях має розв’язки:
-
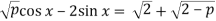 .
.
Відповідь: ![]()
-
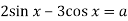 .
.
Відповідь:![]()
3. ![]() . Відповідь:
. Відповідь:![]()
4. ![]()
Відповідь: ![]()
5.![]() .
.
Відповідь: ![]()
6. ![]()
Відповідь: ![]()
Знайдіть всі значення параметру, при яких рівняннях не має рішень:
7.![]()
Відповідь: ![]()
8.![]()
Відповідь: ![]()
1.3 КІЛЬКІСТЬ КОРЕНІВ РІВНЯННЯ.
У цьому пункті розглядатимуться деякі приклади на визначення кількості коренів рівняння. Найбільш часто зустрічаються завдання в яких потрібно визначити значення параметру при якому рівняння має певну кінцеву кількість коренів. Через те що зазвичай тригонометричні рівняння (в силу періодичності тригонометричних функцій) мають цілу серію рішень, то в умові вказується певний проміжок, якому повинні належати корені рівняння.
Приклад 1.3.01При яких значеннях параметра ![]()
![]()
має більш ніж один корінь на проміжку ![]() ?
?
Розв’язання.
Нехай ![]() , тоді
, тоді
![]()
(![]()
Тоді рівняння набуває вигляду
![]()
![]()
![]()
![]()
-
Розглянемо рівняння при
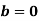
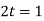
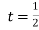 .
.
Тоді рівняння ![]() ;
;
![]() ;
;
![]()
Має єдиний корінь ![]() на проміжку
на проміжку ![]() ,
,
що не задовольняє умову задачі.
-
Розглянемо рівняння при
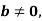
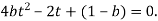
![]() ,
,
![]()
![]()
![]() ,
, ![]()
За умовою задачі нам потрібно, щоб рівняння мало більше ніж один корінь на інтервалі ![]() , тобто має виконуватися нерівність
, тобто має виконуватися нерівність
![]()
Отже, рівняння матиме більше ніж один корінь на проміжку ![]() , за виконання умов:
, за виконання умов:
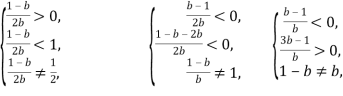
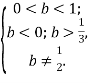
Звідки маємо: ![]()
Відповідь: При ![]()
Приклад 1.3.02. Знайдіть усі значення параметра а, при яких рівняння ![]() має шість коренів.
має шість коренів.
Розв’язання.
Рівняння ![]() рівносильне рівнянню
рівносильне рівнянню
![]()
При ![]() рівняння не має коренів.
рівняння не має коренів.
При ![]()
Розглянемо рівняння при ![]() .
.
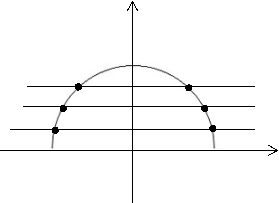
Графіком рівняння ![]() є півколо з центром у точці О (0;0), радіусом R=
є півколо з центром у точці О (0;0), радіусом R=![]() .
.
Графіком рівняння ![]() є прямі, паралельні осі абсцис. Наприклад,
є прямі, паралельні осі абсцис. Наприклад,
у
![]()
![]()
![]()
![]()
x
Якщо ![]()
![]()
Отже, при ![]() рівняння матиме шість коренів.
рівняння матиме шість коренів.
Відповідь: При ![]()
![]() .
.
Приклад 1.3.03. При яких значеннях a рівняння![]()
має тільки три кореня на відрізку ![]()
Розв’язання.
Виносячи спільний множник, отримаємо рівняння ![]()
Нехай спочатку ![]() .
.
Тоді при ![]() можна отримати три кореня
можна отримати три кореня ![]() , лежачих на даному відрізку
, лежачих на даному відрізку ![]()
Це означає, що другий множник не дорівнює нулю при ![]()
![]()
Якщо ![]() , то коренями другого множника будуть числа
, то коренями другого множника будуть числа ![]() і хоча б один з них потрапить на відрізок
і хоча б один з них потрапить на відрізок ![]() .
.
Отже, має бути ![]() звідки отримуємо
звідки отримуємо
![]()
Відповідь: ![]()
Розв’яжіть самостійно.
1.При яких значеннях параметра a рівняння
![]()
має рівно чотири кореня на відрізку ![]()
Відповідь.![]() .
.
2. Знайдіть усі значення параметру ![]()
![]()
має рівно три корені, що належать проміжку ![]() ?
?
Відповідь.![]()
-
Знайдіть найменше значення параметру
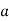
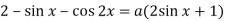 має на інтервалі
має на інтервалі 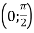 єдиний розв'язок.
єдиний розв'язок.
Відповідь.![]()
4. При яких значеннях параметра a рівняння
![]()
має на проміжку ![]() не менш 3 коренів?
не менш 3 коренів?
Відповідь.![]()
§2.Нерівності з параметрами.
Приклад 2.01.При якому найменшому значенні параметру a нерівність ![]()
має хоча б єдиний розв’язок?
Розв’язання.
Розглянемо наступні випадки:
Випадок 1: ![]()
Якщо a < –1, то скористаємося наступними нерівностями:
![]() ;
;
![]() .
.
Додавши ці нерівності, отримаємо, що![]()
![]() ,
,
![]() .
.
Тому при ![]()
Якщо ![]()
![]()
![]() .
.
Відповідь: a = –1.
Приклад 2.02 При яких значеннях параметра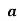
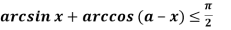 має рішення?
має рішення?
Розв’язування.
![]() ;
;
![]() .
.
Скористаємося тотожністю ![]() . Отримаємо
. Отримаємо
![]()
Так як функція ![]()
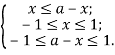
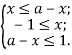
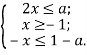
![]()
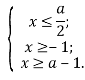
Треба розглянути питання взаємного розташування на числовій прямій точок ![]()
![]()
Отже, остання система має рішення, якщо і тільки якщо: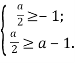
Тобто, ![]()
![]()
При ![]()
![]() має рішення.
має рішення.
Відповідь: ![]()
Приклад 2.03. При всіх значеннях параметра a розв’язати нерівність
![]() .
.
Розв’язування.
Перетворимо нерівність:
![]()
![]()
![]()
Скористаємося тим, що ліва частина останньої нерівності не перевищує 1, а його права частина завжди не менше, ніж 1. Тому нерівність рівносильна наступній системі рівнянь:
![]()
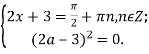
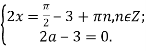
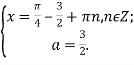
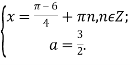
Відповідь: Якщо ![]()
Якщо ![]() .
.
Приклад 2.04. При яких значеннях параметра a нерівність
![]()
має кінцеве додатне число рішень на інтервалі ![]()
Розв’язування.
![]() ;
;
![]() ;
;
![]() ;
;
![]()
Розглянемо наступні випадки:
Випадок1: ![]()
Якщо ![]()
![]()
![]()
![]()
![]()
Корні рівняння , які входять до інтервалу![]()
![]()
Отже, останнє рівняння має кінцеве додатне число рішень на інтервалі ![]()
![]()
Випадок 2: ![]()
Нехай ![]() Отримаємо квадратну нерівність:
Отримаємо квадратну нерівність:
![]()
Розв’яжемо рівняння ![]()
![]()
![]() ;
; ![]()
Якщо ![]()
![]() . Врахуємо, що гілки параболи
. Врахуємо, що гілки параболи ![]() спрямовані вниз. Тому рішення квадратного нерівності задаються сукупністю
спрямовані вниз. Тому рішення квадратного нерівності задаються сукупністю
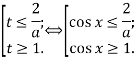
-
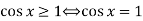 і має кінцеве позитивне число рішень на інтервалі
і має кінцеве позитивне число рішень на інтервалі 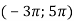
-
Тоді треба,щоб нерівність
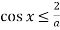 чи зовсім не мала рішень на інтервалі
чи зовсім не мала рішень на інтервалі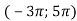
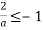 , тобто
, тобто 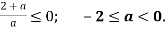
Випадок 3: ![]()
Нехай ![]() Отримаємо квадратну нерівність:
Отримаємо квадратну нерівність: ![]()
Якщо ![]()
![]() та
та ![]()
Врахуємо, що гілки параболи ![]() спрямовані до верху. Але треба розглянути, два випадки взаємного розташування коренів рівняння.
спрямовані до верху. Але треба розглянути, два випадки взаємного розташування коренів рівняння.
-
Якщо
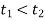 , тобто
, тобто 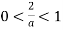 ;
; 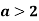
Маємо ,що при ![]()
![]() , тобто
, тобто ![]() .
.
![]()
Ця нерівність має на інтервалі ![]()
2) Якщо ![]() , тобто
, тобто ![]() ;
; ![]() то отримаємо
то отримаємо ![]()
Тоді при ![]()
![]() ,
, ![]()
![]()
Ця нерівність рівносильна рівнянню ![]()
![]()
Відповідь: ![]()
Розв’яжіть самостійно.
1.При яких значеннях параметра![]()
![]()
має кінцеве додатне число рішень на інтервалі ![]()
Відповідь: ![]()
2.Знайдіть всі значення параметра а, при яких для будь-якого дійсного значення х виконується нерівність
![]()
Відповідь: ![]()
§3. Завдання підвищеної складності
Приклад. Для кожного значення параметру ![]()
![]()
Розв’язування.
![]()
![]()
![]()
![]()
![]() ;
;
![]() ;
;
![]()
або ![]()
Нехай ![]() тоді
тоді
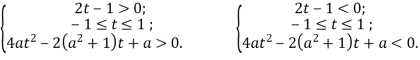
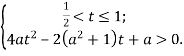 (1)
(1) 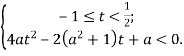 (2)
(2)
Якщо ![]()
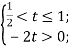 або
або 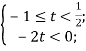
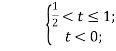
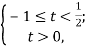
![]()
Отже, якщо ![]()
![]()
При ![]()
Введемо функцію![]() Різні можливі випадки визначаються знаками функції
Різні можливі випадки визначаються знаками функції ![]() в точках
в точках ![]() , знаком
, знаком ![]()
![]() .
.
Маємо: ![]()
![]() ;
;
Так як ![]() =
= ![]() , то екстремум функції знаходиться в точці
, то екстремум функції знаходиться в точці ![]()
і є мінімумом при ![]()
![]()
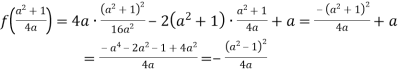
Рівняння ![]() має два дійсних корні (при
має два дійсних корні (при ![]()
![]()
![]()
Порівняємо ![]() .
.
Знайдемо їх різницю ![]() .
.
![]()
![]()
Значить , ![]()
![]() , якщо
, якщо ![]() і
і ![]() При
При ![]()
![]() .
.
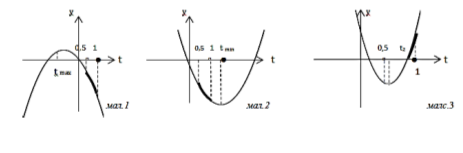 Значення функції
Значення функції ![]() в точках
в точках ![]() и в точці екстремуму зміняють знак при значенні
и в точці екстремуму зміняють знак при значенні ![]()
![]()
![]() Тому розіб'ємо числову пряму на наступні проміжки:
Тому розіб'ємо числову пряму на наступні проміжки: ![]() .
.
1)Якщо ![]()
![]() . Від'ємне значення і у точки екстремуму
. Від'ємне значення і у точки екстремуму![]() , тобто не належить проміжку
, тобто не належить проміжку ![]() . А значення в точці екстремуму (сам екстремум) приймає додатні значення
. А значення в точці екстремуму (сам екстремум) приймає додатні значення ![]() У цьому випадку (мал.1) функція
У цьому випадку (мал.1) функція ![]() від'ємна у всіх точках проміжку
від'ємна у всіх точках проміжку ![]() . Система не має рішень на даному проміжку.
. Система не має рішень на даному проміжку.
2)Якщо ![]() , то
, то ![]() . Точка екстремуму - точка мінімуму додатна
. Точка екстремуму - точка мінімуму додатна
![]() і лежить поза проміжку
і лежить поза проміжку ![]() , а значення в ній від’ємне
, а значення в ній від’ємне ![]() Отримуємо, що (мал.2)
Отримуємо, що (мал.2) ![]() від'ємна у всіх точках проміжку
від'ємна у всіх точках проміжку![]() Наша система і для цих значень a не має рішень.
Наша система і для цих значень a не має рішень.
-
Якщо
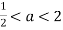 ,то
,то 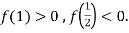
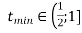 , а
, а 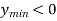
Функція має тільки один корінь на ![]() , а саме
, а саме ![]() (рис.3). Значить, враховуючи заданий інтервал, функція додатна на
(рис.3). Значить, враховуючи заданий інтервал, функція додатна на ![]() .
.
Так як якщо ![]() ,то значення
,то значення ![]() змінюється залежно від значення a. Розіб’ємо цей інтервал на два.
змінюється залежно від значення a. Розіб’ємо цей інтервал на два.
Якщо ![]() то
то ![]() , тобто
, тобто ![]() .
.
Якщо ![]()
![]() , тобто
, тобто ![]()
![]()
![]()
![]()
4) Якщо ![]()
![]() . Точка мінімуму належить проміжку
. Точка мінімуму належить проміжку ![]() , а сам мінімум від’ємний, то на нашому інтервалі функція
, а сам мінімум від’ємний, то на нашому інтервалі функція ![]() додатні значення не приймає.
додатні значення не приймає.
5) Відзначимо, що при ![]() система не має рішень.
система не має рішень.
Отже, якщо ![]() , то рішень не має.
, то рішень не має.
![]() .
.
![]()
![]()
II.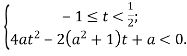
 Різноманітні можливі випадки визначаються знаками функції
Різноманітні можливі випадки визначаються знаками функції ![]() в точках
в точках
![]() , знаком
, знаком ![]()
![]() .
.
Маємо:![]() .
.
Екстремум функції знаходиться в точці ![]()
І ![]() .
.
Значення функції ![]() в точках
в точках ![]() и в точці екстремуму змінює знак при таких значеннях
и в точці екстремуму змінює знак при таких значеннях ![]()
![]()
![]()
Тому числову пряму розіб’ємо на проміжки:
![]()
![]()
-
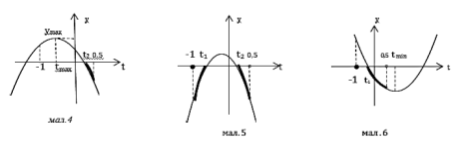
Якщо
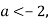
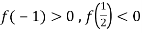 . Від’ємна точка екстремуму
. Від’ємна точка екстремуму 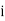
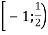 . А значення в точці екстремуму (максимуму) додатне,
. А значення в точці екстремуму (максимуму) додатне, 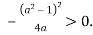
Функція має тільки один корінь на ![]() , а саме
, а саме ![]() Отже, враховуючи заданий інтервал, функція від’ємна на
Отже, враховуючи заданий інтервал, функція від’ємна на ![]() . Якщо
. Якщо ![]()
![]() . Тоді,
. Тоді,![]() і
і ![]() .
.
2)Якщо ![]() , то
, то ![]() . Точка екстремуму - точка максимуму - від’ємна
. Точка екстремуму - точка максимуму - від’ємна![]() и належіть проміжку
и належіть проміжку ![]() , а значення в ній додатне
, а значення в ній додатне![]()
Получаємо, що функція має два корені на ![]() Від’ємна вона, якщо
Від’ємна вона, якщо ![]() .
.
Так я інтервал ![]() містить
містить ![]()
![]() різні на різних частинах проміжку.
різні на різних частинах проміжку.
Якщо ![]()
![]() .
.
Якщо ![]() , то
, то ![]()
При ![]()
![]() .
.
Отже,![]()
3) Якщо ![]() , то
, то ![]() Точка максимуму від’ємна и не належить проміжку
Точка максимуму від’ємна и не належить проміжку ![]() . Значення у ній -
. Значення у ній - ![]() . Функція має тільки один корінь на
. Функція має тільки один корінь на ![]() , а саме
, а саме ![]() Значить, враховуючи заданий інтервал, функція від’ємна на
Значить, враховуючи заданий інтервал, функція від’ємна на ![]() .
.
Так я ![]() , то
, то![]() і
і ![]() ,
, ![]() .
.
4) Якщо ![]()
![]() .
. ![]()
![]() ,
, ![]() .
.
Значить, функція має тільки один корінь на ![]() , а саме
, а саме ![]() Тоді функція
Тоді функція ![]() від’ємна на
від’ємна на ![]() .
.
Якщо ![]()
![]() .
. ![]() і
і ![]()
![]()
![]() .
. ![]() ,
, ![]() .
.
При ![]()
![]() Функція від’ємною не може бути.
Функція від’ємною не може бути.
5) При ![]()
![]() .
. ![]() ,
, ![]() . Значить, функція на нашому інтервалі має еще один корінь
. Значить, функція на нашому інтервалі має еще один корінь ![]() . Вона від’ємна на
. Вона від’ємна на ![]()
Так як ![]() получимо
получимо ![]() .
.
6) Аналогічно получаємо, при ![]()
![]() А именно
А именно ![]()
Отже, ми з’ясували рішення другої системи:
якщо![]()
![]() .
.
![]()
![]()
![]() .
.
![]()
Об’єднаємо отримані рішення двох систем. Маємо:
при ![]()
при![]()
при![]()
при ![]()
при ![]() ;
;
при ![]()
![]() .
.
Додаємо, що при ![]()
![]() . І звернемося до заміни
. І звернемося до заміни ![]() .
.
При ![]() Так як
Так як ![]()
![]()
![]() завжди із проміжку
завжди із проміжку ![]() , то
, то
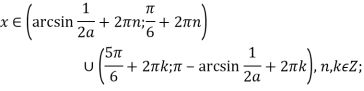
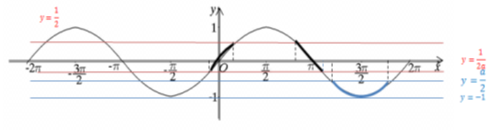 при
при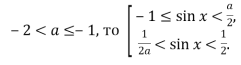 Так як для цих
Так як для цих ![]()
![]() , то
, то
![]()
![]() ( мал.7)
( мал.7)
при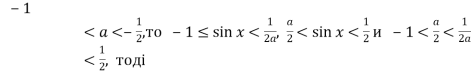
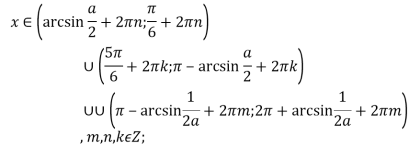
при ![]() Так як
Так як ![]() , то
, то
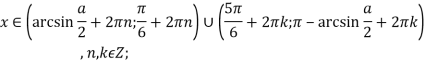
при 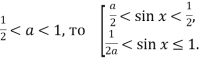 Так як,
Так як, ![]() то
то

при ![]()
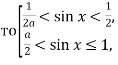
![]()
![]()
![]()
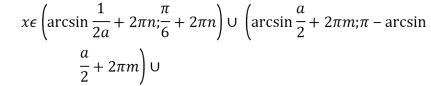
![]() ;
;
![]()
при ![]()
![]()
![]()
Відповідь:
При ![]()
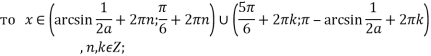
При![]()
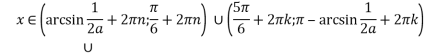
![]()
при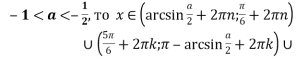
![]()
при ![]()
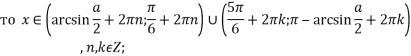
при ![]()
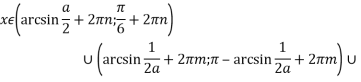
![]()
при ![]()
![]()
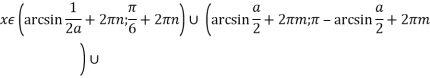
![]() ;
;
при ![]()
![]()
СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ.
- Нелин Е.П. Алгебра и начала анализа : учеб. для 10 кл. общеобразоват. учебн. заведений: академ. уровень. [Текст] / Е.П. Нелин // Х.: Гимназия, 2010.-416 с.
- Локоть В.В. Задачи с параметрами и их решение. [Электронный ресурс] / В.В. Локоть // Тригонометрия: уравнения, неравенства, системи.10 класс. – 3-изд., испр. и доп.- М.: АРКТИ,2008.- 64с.– Режим доступа: http://edu-lib.net/matematika-2/dlya-shkolnikov/lokot-v-v-zadachi-s-parametrami-i-ih-re.
- Ястребинецкий Г.А. Задачи с параметрами [Текст] / Г.А. Ястребинецкий // М.,1986. – 127 с.
- Горнштейн П.И. Задачи с параметрами [Текст] / П.И. Горнштейн, В.Б. Полонский, М.С. Якир. // М.: Илскса, Харьков: Гимназия, 2005. ‑ 328 с.
- Козко А. И. Задачи с параметром и другие сложные задачи [Текст] / А. И. Козко, В. Г. Чирский // М.: МЦНМО, 2007. — 296 с.
- Захарійченко Ю.О., Репета В.К., Макарова І.С., Карпік В.В. Математика ЗНО-2015,або в Новий рік за новими правилами. Математика в школах України. Науково-методичній журнал: №6, №7-8, 2015.
- В.М.Чорна Параметри в шкільному курсі математики. Методичні поради. Математика в школах України. Науково-методичній журнал: №7-8, 2015.

52
-
-
Актуально


про публікацію авторської розробки
Додати розробку
