Конспект уроку алгебри в 10 класі "Метод інтервалів"

Тема. Метод інтервалів.

Мета. Освітня: навчити розв’язувати раціональні нерівності методом інтервалів.

           Розвивальна: розвивати вміння переносити набуті знання у нові ситуації;

           стимулювати учнів до висловлювань без побоювання помилитись.

           Виховна: виховувати культуру математичної мови, намагатися скласти

           ситуацію успіху для кожного учня.

Тип уроку: урок засвоєння нових знань.

Хід уроку

І. Організаційний момент. Привітання.

ІІ. Перевірка домашнього завдання.

№ 12.17

1. D(у) = (-∞; -1,5] U [6; +∞).  2) D(у) = (-3;5).

№  12.22

1. (-∞;1/2) U [5/3;3).  2)(-2;0] U [5;9).

№ 12.29

     1)(-6;-3) U (-2;1).  2)(-1 -√5;2) U (-2;-1+√5).  3)(-5;3+2√2)

ІІІ. Мотивація навчальної діяльності учнів.

      Ви ознайомилися із розв’язуванням нерівностей другого степеня з однією змінною графічним і аналітичним способами. Виникає питання: як роз’язати нерівність вище другого степеня з однією змінною? Такі нерівності розв’язувати важко. Однак, якщо відомий розклад многочленна на множники, такі нерівності можна розв’язати методом інтервалів досить просто. Сьогодні ми розглянемо такий спосіб розв’язування нерівностей.

ІV. Актуалізація опорних знань. Бліц-опитування.

1. Розв’язати рівняння:
   а) (х-3)(х-7)(Х-√2) = 0;
   б) (ΙхΙ-2)(х-3) = 0;
2.  Коли добуток а*b ,буде:
   а) більшим від нуля;
   б) меншим від нуля.

 

V. Пояснення нового матеріалу. 

Квадратні нерівності, які ви навчились розв’язувати на попередніх уроках, є окремим випадком раціональних нерівностей.

Означення. Нерівність, ліва і права частини якої є раціональними виразами, називається раціональною.

Як відомо, будь-який раціональний вираз можна подати у вигляді раціонального дробу. Тому для того, щоб навчитися розв’язувати раціональні нерівності, достатньо навчитися розв’язувати нерівності виду

                          

 

 

 

 

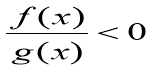
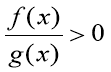
            Де f(x), g(x) – многочлени.

Розглянемо графік деякої функції f, у якої D(f) =R, х_1,  х₂, х₃  - нулі функції,

(-∞;х₁ ), (х_1,  х₂), (х₂, х₃), (х₃;+ ∞) проміжки знакосталості.

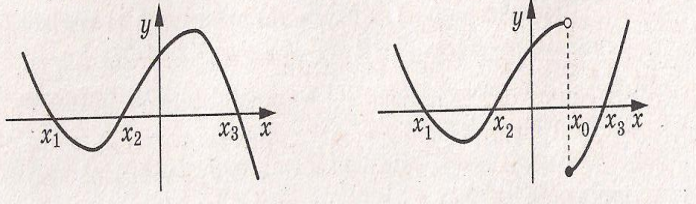
А чи завжли нулі функції розбивають її  область визначення на проміжки знакосталості? Ні. Для функції g проміжок (х₂, х₃) не є проміжком знакосталості. Якщо хє (х₂, х_о), то g(х)>0, а якщо хє(х_0;х₃), то g(х)<0.

Принципова відмінність між функціями f і g полягає в тому, що графіком функції f є неперервна крива, а графік функції g такої властивості не має. Говорять,що функція f неперервна в кожній точці області визначення, або як ще прийнято говорити, неперервна на D(f), а g у точці х₀ має розрив.

    Більш детально з поняттям неперервності функції ви ознайомитесь в старших класах. Там же буде і доведена така теорема.

Теорема 13.1. Якщо функція f неперервна і не має нулів на деякому проміжку, то вона на цьому проміжку зберігає постійний знак.

   Ця теорема дозволяє не будуючи графіка функції f, розв’язати нерівності f(x) >0, f(x) <0.

   Уявімо собі, що з рисунка зникли всі точки функції f за винятком точок А(х₁;0),

В(х₂ ;0), С(х₃;0). Очевидно, що кожний з проміжків (-∞;х₁ ), (х_1,  х₂), (х₂, х₃), (х₃;+ ∞) не містить нулів функції. Тоді, пам’ятаючи, що функція f неперервна на D(f), можна стверджувати: вказані проміжки є проміжками знакосталості функції f. Залишається лише з’ясувати, якого знака набувають значення функції f на цих проміжках. Це можна зробити за допомогою «пробних» точок. Нехай, наприклад, а є (-∞;х₁ ) і f(a) >0. Тоді для будь-якого х є (-∞;х₁ ) виконується нерівність f(x) >0. Аналогічно можна «взяти пробу» з кожного проміжку знакосталості.

   Описаний метод розв’язування називають методом інтервалів.

Теорема 13.2.

Функція  у= f(x)/g(x), де f(x) і g(x) - многочлени, неперервна на D(y).

   Ця теорема теорема дозволяє для нерівностей виду f(x)/g(x) >0,    f(x)/g(x) <0 , де f(x) і g(х) - многочлени методом інтервалів.

Приклад 1.(х+3)(х-1)(х-2) >0. Розв’язання: f(х)= (х+3)(х-1)(х-2), D(f)=R, х=-3, х=1, х=2 – нулі функції

 

Відповідь: (-3;1)U(2 ;+ ∞).

№ 13.3 (х-1)(х+3)²(х-2) <0.

Відповідь:(1;2).

 № 13.7 ((х-2)(х+1))/(х-4) <0

Відповідь: (-∞;-1)U(2;4).

VІ. Закріплення вивченого матеріалу

Робота в групах

Завдання на картках:

1 ряд: №13.1 (2)

2 ряд: № 13.5 (2)

3 ряд: № 13.5 (3).

Хто справиться із завданням, розв’язує № 13.5 (4). Відповідь: (-1/3; 2).

VІІ. Підсумок уроку. Рефлексія.

1. Що нового дізнались на уроці?
2. Чи потрібна ця тема для Вас ?
3. Охарактеризуйте урок трьома словами, запишіть на відривних карточках.

VІІІ. Домашнє завдання. На опорних конспектах.

Середній рівень: № 13.2

Достатній рівень: № 13.4, 13.8(3)

Високий рівень: № 13.6(2,3,5). 13.8(4)