Урок "Система уроків з теми "Тригонометричні рівняння""
Узагальнити методи розв'язування тригонометричних рівнянь, відбір коренів; розвивати вміння творчо мислити, виховувати етику та культуру спілкування.
ОЗ Великочернеччинська спеціалізована школа І-ІІІ ступенів Сумської районної ради Сумської області
Система уроків з теми:
«Тригонометричні рівняння»
Алгебра 10
Вчитель математики
Саранчук О. В.
Урок 1-2
Тема: Розвʼязування найпростіших тригонометричних рівнянь.
Мета: познайомити учнів з методами розв’язування тригонометричних рівнянь, а також з різними способами запису множини коренів рівняння. Розвивати логічне мислення, виховувати акуратність та наполегливість.
ХІД УРОКУ
І. Оголошення мети уроку.
Сьогодні на уроці ми вивчатимемо рівняння, в записах яких є тригонометричні функції. Існує багато різних способів розв’язання тригонометричних рівнянь, але ці методи об’єднує те, що всі тригонометричні рівняння зводяться до найпростіших. Тому вміння розв’язувати найпростіші рівняння – це перший крок до розв’язання більш складних.
ІІ. Нова тема.
До найпростіших тригонометричних рівнянь відносяться рівняння виду ![]()
а) Розв’яжемо рівняння ![]()
![]() . Нехай
. Нехай ![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
з урахуванням періодичності приходимо до формули:
![]()
![]()
![]() б) Знайомство з розвʼязанням рівнянь виду
б) Знайомство з розвʼязанням рівнянь виду ![]()
![]() також починаємо з розвʼязання рівняння
також починаємо з розвʼязання рівняння ![]()

![]()
![]()
![]()
![]()
![]()
![]()
з урахуванням періодичності приходимо до формули:
![]() , якщо
, якщо ![]()
Після цього розвʼязуємо рівняння:
![]()
![]()
![]()
![]()
в) Розв’язування вправ №460 (стор. 217, алгебра 10 клас, Шкіль, Колесник, 2000 рік )
г) Розвʼязуємо рівняння ![]()
ІІІ. Розв’язування вправ.
1). Розглянемо рівняння виду: ![]()
Наприклад:
а) ![]() , тоді
, тоді
![]()
![]() ;
; ![]() ;
;
![]() ;
;
![]()
![]()
![]()
![]()
б) ![]() Дане рівняння рівносильне рівнянню:
Дане рівняння рівносильне рівнянню:
![]()
![]()
![]()
![]()
так як ліва частина не менше нуля, то і ![]() , отже
, отже ![]()
![]() , де
, де
![]()
в) Знайти помилку в розв’язанні : ![]()
Так як ![]()
![]()
Помилка в тому, що функція ![]() не є періодичною. Правильна відповідь:
не є періодичною. Правильна відповідь:
![]()
![]()
![]()
![]()
![]()
2) Розглянемо рівняння виду ![]()
![]()

![]() І спосіб
І спосіб
![]()
![]()
![]()
![]()
![]()
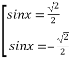
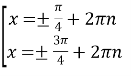
![]()
ІІ- спосіб
Використовуємо формулу пониження степеня: ![]()
![]() ;
; ![]() ; 1-cos2x=1 ; cos2x=0
; 1-cos2x=1 ; cos2x=0
2x=![]() ; x=
; x=![]() .
.
Доводимо, що розвʼязки в першому і другому способах співпадають.
Звертаємо увагу на те, що розвʼязки першого рівняння можна обʼєднати в одну серію розвʼязків другого рівняння.
Наприклад:
розв’язком деякого рівняння є ![]() .
.
Знайдемо обʼєднання ![]() . Ці множини мають спільні елементи. Запишемо їх:
. Ці множини мають спільні елементи. Запишемо їх: ![]()
![]()
![]() ;
; ![]() ;
; ![]()
![]() ;…
;…
Тобто множина ![]() міститься в множині
міститься в множині ![]() . Отже загальна відповідь
. Отже загальна відповідь ![]() .
.
3) Розвʼязати систему рівнянь:
![]() ;
; ![]() ;
; 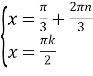
![]()
Для написання відповіді необхідно знайти перетин серій розв’язків.
Відповідь: ![]()
ІV. Самостійна робота.
І варіант ІІ варіант
№403(а) №403(б)
№406(а) №406(б)
№409(а) №409(б)
№415(а) №415(б)
Вправи за збірником екзаменаційних завдань. Алгебра 11 клас. Донецьк-1997.
V. Підсумок. Домашнє завдання.
Опрацювати п.38, розв’язати : А: №463 , Б: №464(а-г) , В: №465(в,г).
Урок 3-4
Тема: Методи розв’язування тригонометричних рівнянь
Мета: Узагальнити методи розв’язування тригонометричних рівнянь, відбір коренів; розвивати вміння творчо мислити, виховувати етику та культуру спілкування.
ХІД УРОКУ
І. Актуалізація опорних фактів
Розв’язати усно: а) 3![]()
б) 4 ![]()
в) 2 sin3x-2=0
г) sin2x=![]()
д) ![]()
ІІ. Нова тема
Складаємо схему розв’язування тригонометричних рівнянь.
- Спробуємо звести всі тригонометричні функції до одного і того ж аргументу.
- Якщо всі функції вдалося звести до одного аргументу, то спробуємо всі тригонометричні вирази записати у вигляді однієї функції.
- Якщо до одного аргументу вдалося звести, а до однієї функції ні, то спробуємо звести рівняння до однорідного.
- В інших випадках переносимо всі члени в одну частину і пробуємо розкласти на множники, або використовуємо спеціальні прийоми розв’язування.
- Якщо потрібно, проводимо відбір коренів на періоді, спільному для всіх функцій, і записуємо відповідь.
ІІІ. Розвʼязування вправ.
Колективно біля дошки розв’язуємо рівняння:
№1. ![]()
![]() (зводимо до однієї функції)
(зводимо до однієї функції)
![]()
![]() . Позначимо
. Позначимо ![]()
![]()
![]()
![]()
![]()
![]()
Відповідь: ![]()
№2. ![]()
![]()
![]()
![]()
2![]()
![]()
![]()
![]()
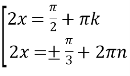 ;
;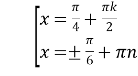 ; n,k
; n,k![]()
№3. ![]() (зводимо до однорідного)
(зводимо до однорідного)
![]()
Якщо ![]()
![]()
![]()
Поділимо ліву і праву частини рівняння на ![]() . Маємо
. Маємо
![]()
![]() ;
; 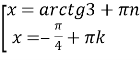 ; n,k
; n,k![]()
№4. ![]()
Використовуємо формулу ![]() , маємо:
, маємо:
![]()
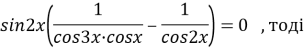
![]()
![]()
Розв’язуємо перше рівняння: ![]()
Розв’язуємо друге рівняння: ![]() (ОДЗ не записуємо, зробимо потім перевірку )
(ОДЗ не записуємо, зробимо потім перевірку )
![]()
![]()
![]()
![]()
![]()
2![]()
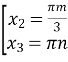 m,n
m,n![]()
В інтервалі ![]() трьох множин розв’язків, попадають тільки числа 0 ;
трьох множин розв’язків, попадають тільки числа 0 ; ![]() ;
; ![]() ; ;
; ; ![]() . Виконавши перевірку, переконуємося, що
. Виконавши перевірку, переконуємося, що ![]()
Відповідь : ![]() k
k![]()
№5. Спеціальні прийоми розв’язування тригонометричних рівнянь.
![]()
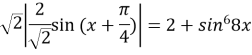
2![]()
Оцінимо множину значень функцій в лівій і правій частинах рівняння. Позначаємо функції в лівій і правій частині рівняння через f![]() g(x)=
g(x)=![]() .
.
Так як, ![]()
![]() , то
, то ![]()
![]()
![]()
![]() , тому
, тому
![]()
![]()
Отже, рівняння рівносильне системі: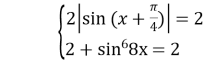 ;
;
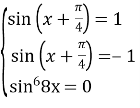 ;
; 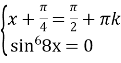 ;
; 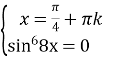
Перевіримо, чи задовольняє розвʼязок першого рівняння друге рівняння. Якщо ![]() то
то ![]()
![]()
Отже, ![]()
Відповідь: ![]()
Розв’язати: №467(а,б,д) і №468(а,б,д)
ІV. Самостійна робота
І варіант ІІ варіант
№ 466(а,г,є) №466(б,д,ж)
V. Підсумок уроку. Домашнє завдання
а) №467-468(ІІ стовпчик) б) №471(а-в)
Урок 5
Тема: Розвʼязування тригонометричних рівнянь.
Мета: узагальнити методи розв’язування тригонометричних рівнянь, відбір коренів; розвивати творчо мислити, виховувати етику та культуру спілкування.
ХІД УРОКУ
І. Перевірка домашнього завдання.
ІІ. Розв’язування вправ колективно біля дошки.
а) рівняння які зводяться до алгебраїчних:
3(1-![]()
![]()
3-3![]()
![]()
1-3![]()
![]()
2![]()
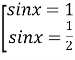 ;
; 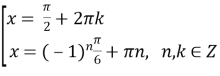
б) Пониження степені в тригонометричних рівняннях:
![]()
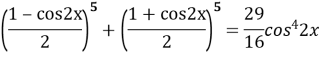
Позначимо ![]()
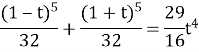
![]() Розкриваємо дужки використовуючи 5 рядок трикутника Паскаля.
Розкриваємо дужки використовуючи 5 рядок трикутника Паскаля.
![]()
![]()
![]() Підстановка
Підстановка ![]()
![]()
![]() ;
; ![]()
![]() ;
; ![]()
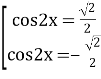 ;
; 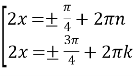 ;
; 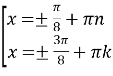 ;
; ![]()
Використовуючи одиничне коло запишемо відповідь: ![]() .
.
в) Рівняння, які зводяться до алгебраїчних за допомогою заміни
![]()
![]() Нехай
Нехай ![]()
![]() ;
; ![]()
Підставляємо в задане рівняння, маємо:
![]() ;
; ![]() ;
; ![]() маємо:
маємо:
-
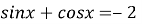
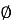
-
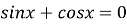
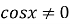
![]()
![]() ,
, ![]()
![]()
![]() ; ОДЗ:
; ОДЗ: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
д) Універсальна підстановка. Цей метод вимагає використання формул:
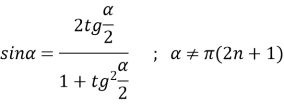
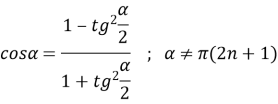
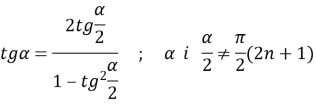
Основна перевага – в будь-якому випадку отримаємо одну тригонометричну функцію ![]() .
.
Недоліки:
а) часто отримуємо рівняння високого степеня;
б) заміна може привести до втрати коренів.
Наприклад:
Розвʼязати рівняння: ![]()
ОДЗ: ![]()
![]() . Нехай
. Нехай ![]()
![]()
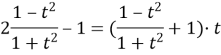
![]() Один із коренів рівняння дорівнює -1. Тоді
Один із коренів рівняння дорівнює -1. Тоді
![]() 1 -3 -3 1
1 -3 -3 1
![]() -1 4 -1
-1 4 -1
-1 1 -4 1 0
(![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Чи була втрата коренів? Ні, так, як початкове рівняння містило ![]()
ІІІ. Підсумок уроку. Домашнє завдання.
За збірником завдань для екзамену з математики «Алгебра і початки аналізу», Донецьк, 1997 р.
Б: № 443-453(б) ; В: №552-525(б)
Урок 6-7
Тема: Розв ![]()
Мета: Узагальнити методи розв’язування тригонометричних рівнянь.
Перевірка знань.
ХІД УРОКУ
І. Перевірка домашнього завдання. Актуалізація опорних знань.
Доповнити розв’язання рівняння:
(![]() )(
)(![]() ) (3+sinz)=4 ОДЗ:
) (3+sinz)=4 ОДЗ:
![]() ;
; 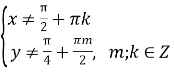
Запишемо рівняння в вигляді: (![]() )
)![]() · (3+sinz)=4
· (3+sinz)=4
Щоб рівність виконувалася, необхідно, щоб добуток трьох множників лівої частини дорівнювала 4, а це можливо, коли 2·1·2. Отже:
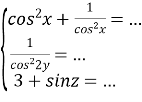 ;
; 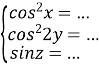 ;
; 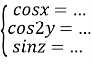 ;
; 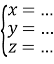
ІІ Розвʼязування вправ.
Учні працюють в трьох групах. Можна використати гру «Лабіринт». По сигналу капітани підкидають грального кубика, числа, які випали на гранях і будуть стартовими номерами рівнянь, які потрібно виконати, далі стрілка підкаже, над яким завданням слід працювати, переможці отримають оцінки високого рівня.
Завдання взяті із збірника під редакцією М. І. Сканаві
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
І група |
8.035 |
8.038 |
8.045 |
8.055 |
8.059 |
8.083 |
|
ІІ група |
8.013 |
8.014 |
8.020 |
8.021 |
8.022 |
8.024 |
|
ІІІ група |
8.182 |
8.183 |
8.201 |
8.203 |
8.208 |
8.211 |
ІІІ. Самостійна робота.
І варіант ІІ варіант
-
2
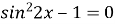 1) 1-2
1) 1-2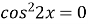
-
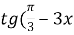 )
)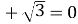 2)
2) 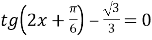
-
4-4(
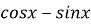
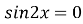
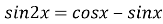
-
8
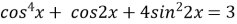 4)
4) 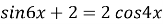
-
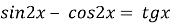
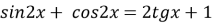
-
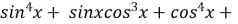 6)
6) 
+![]()
Додатково: М.І. Сканаві група В: №8.421; №8.422; №8.431
ІV. Підсумок уроку. Домашнє завдання.
Розв’язати за збірником екзаменаційних завдань з математики «Алгебра і початки аналізу», Донецьк, 1997 р.
№487-489(б) ; №534-537(б)
Урок 8
Тема: Контрольна робота.
Мета: Перевірка знань.
Розв’язати за збірником екзаменаційних завдань з математики «Алгебра і початки аналізу», Донецьк, 1997 р.
І варіант ІІ варіант
№ 418(а) № 418(б)
№ 419(а) № 419(б)
№ 421(а) 3 бали № 421(б)
№ 432(а) № 432(б)
№ 434(а) № 434(б)
№ 435(а) № 435(б)
№ 449(а) № 449(б)
№ 452(а) № 452(б)
№ 457(а) 5балів № 457(б)
№ 462(а) № 462(б)
№ 472(а) № 472(б)
№ 474(а) № 474(б)
№ 524(а) № 524(б)
№ 528(а) № 528(б)
№ 529(а) 4 бали № 529(б)
№ 538(а) № 538(б)


про публікацію авторської розробки
Додати розробку
