МЕТОДИЧНИЙ ПОСІБНИК

Як зацікавити математикою

сучасного  здобувача освіти

            Автор досвіду:

                                            Пархомчук О.І., вчитель математики

                                                Бистріївської гімназії   Вчорайшенської сільської ради

               Бердичівського району                                

2024

Методичний посібник

     В методичному посібнику розглядаються деякі підходи до формування пізнавального інтересу до вивчення  математики за допомогою інформаційно-комунікаційних технологій та окремих форм і методів. Розкрито інноваційні підходи до подачі матеріалу на уроках математики. Представлені інструменти формування в здобувачів освіти зацікавленості до вивчення предмету, показано роль  та умови реалізації розвивальних ігор та використання знань з математики у реальному житті. Наведено приклади  деяких задач практичного змісту на вартість життя та творчих завдань для самостійного опрацювання, що підвищують зацікавленість предметом.

     Розраховано на вчителів математики, яких хвилюють питання як показати учасникам освітнього процесу важливість математичних знань  у їхньому повсякденному житті та зацікавити сучасного школяра математикою.

ЗМІСТ

ВСТУП ...................................................................................................................3

РОЗДІЛ 1  ..................................................................................................................4

ПСИХОЛОГО-ПЕДАГОГІЧНІ АСПЕКТИ ФОРМУВАННЯ В УЧНІВ ПІЗНАВАЛЬНОГО ІНТЕРЕСУ ДО ВИВЧЕННЯ МАТЕМАТИКИ    ..................4

РОЗДІЛ 2     ...............................................................................................................9

ІННОВАЦІЙНІ ПІДХОДИ ДО ПОДАЧІ МАТЕРІАЛУ НА УРОКАХ МАТЕМАТИКИ                 ......................................................................................................9

РОЗДІЛ 3   ...............................................................................................................14

ОРГАНІЗАЦІЯ МАТЕМАТИЧНИХ ЗАХОДІВ ЯК ІНСТРУМЕНТ ФОРМУВАННЯ В УЧНІВ ЗАЦІКАВЛЕНОСТІ ДО ВИВЧЕННЯ ПРЕДМЕТУ                         ................................................................................................................14

РОЗДІЛ 4  ................................................................................................................19

РОЗВИВАЛЬНІ ІГРИ ТА ВИКОРИСТАННЯ МАТЕМАТИКИ У РЕАЛЬНОМУ ЖИТТІ: ПРИНЦИПИ ТА УМОВИ РЕАЛІЗАЦІЇ              ..........................................19

РОЗДІЛ 5  ................................................................................................................25

МЕТОДИЧНИЙ МАТЕРІАЛ З МАТЕМАТИКИ ДЛЯ САМОСТІЙНОГО ОПРАЦЮВАННЯ              .............................................................................................25

ВИСНОВКИ .......................................................................................................30

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ  .............................................................31

ВСТУП

Як збадьорити школярів для вивчення математики та як продемонструвати важливість математичних принципів у їхньому повсякденному житті?  Поясненням є те, що вся навколишня дійсність тісно пов'язана з математикою. Наприклад, як визначається заробітна плата дорослих та як управляється сімейний бюджет? Як можна точно розрахувати час прибуття поїзда на будь-яку станцію, який подолав майже всю країну? Які принципи лежать в основі розрахунків кредитних та депозитних відсотків у банку? Чому бджоли будують соти саме шестикутні? Це лише кілька запитань, на які відповіді базуються на математичних принципах. Вивчаючи будь-яку тему з програми, завжди пояснюємо де можна застосувати отримані знання.

Починаючи знайомитися з п’ятикласниками, ми з перших уроків даємо відповідь на питання «для чого нам в житті математика? Чи допоможуть математичні вміння і навички стати успішним в дорослому житті?» На моїх уроках здобувачі освіти не лише розв'язують абстрактні завдання з підручника, але, що найважливіше, формують практичний досвід, який допомагає застосовувати математичні знання в повсякденному житті. Учні розуміють принципи формування рахунків за комунальні послуги, вміють порівнювати витрати та доходи, розраховувати відсоток банківського кредиту та обчислювати вартість доставки покупок. Теоретичні знання завжди повинні мати конкретний практичний зміст! Як домашнє завдання, часто надаю завдання переписати поточні показники лічильників за воду чи газ, розібратися у вартості одиниці обсягу, порівняти ці дані із минулим місяцем, розрахувати суму для оплати відповідних послуг на поточний період. Такі завдання завжди викликають певний ентузіазм, оскільки підлітки відчувають себе дорослими та самостійними, а самостійність в цьому контексті стає джерелом задоволення та підвищує зацікавленість вивченням математики!

РОЗДІЛ 1

ПСИХОЛОГО-ПЕДАГОГІЧНІ АСПЕКТИ ФОРМУВАННЯ В УЧНІВ ПІЗНАВАЛЬНОГО ІНТЕРЕСУ ДО ВИВЧЕННЯ МАТЕМАТИКИ

Важливим методом підвищення якості навчання, запобігання механічному запам’ятовуванню та усунення надмірного навчального навантаження є розвиток пізнавального інтересу. Оскільки учні мотивуються до навчання двома способами: або через зацікавленість предметом і завданнями, які вони вивчають, або через впевненість у тому, що це буде корисним для їхнього майбутнього життя, створення цих двох мотивацій у школярів є основною метою в розвитку їхнього пізнавального інтересу^[1].

Дуже важливою при формуванні пізнавального інтересу в учнів є роль вчителя, його вміння підтримати та пояснити новий матеріал. Варто зауважити, що сучасний вчитель повинен бути не лише педагогом, що пояснює новий матеріал, але й порадником, певною мірою психологом. Діти у міру свого віку та розвитку завжди потребують уваги та підтримки, а тому ключовим чинником при формуванні пізнавального інтересу до навчання є вміння вчителя налаштувати учнівський колектив та, у разі потреби, допомогти та підтримати кожного з учнів.

Роль вчителя в формуванні нового, інформаційного суспільства надзвичайно важлива. Вчитель повинен бути прикладом у невпинному оновленні знань, оволодінні передовими технологіями і розвитку творчого та гуманного мислення. Як представник української інтелігенції, вчитель має об’єднувати глибокі знання та професіоналізм у своїй галузі з моральною чистотою, високою культурою, соціальною толерантністю, стриманістю у поведінці та судженнях.

Учителі в умовах Нової української школи (НУШ) виконують різноманітні функції, які охоплюють різні аспекти освітнього процесу. Вони виступають джерелом знань для учнів під час уроків та в позаурочний час. Також вони відіграють ключову роль у забезпеченні охорони життя та зміцненні здоров'я дітей. Учителі виконують управлінську функцію, організовуючи освітню діяльність учнів та створюючи педагогічні умови для їхнього успішного навчання, розвитку та виховання. Крім того, вони взаємодіють з батьками, забезпечуючи педагогічну освіту для них і регулюючи впливи, які виникають від сім'ї та школи. На рівні класу учителі виконують функції класних керівників, сприяючи загальному розвитку та вихованню своїх учнів^[2].

Суспільний ідеал вчителя нерозривно пов'язаний із формуванням позитивного іміджу педагога, що вимагає наявності вчителем навичок активного створення та постійного удосконалення свого іміджу. Цей процес тісно пов'язаний з професійною компетентністю вчителя і визначає його педагогічну майстерність. Здатність вчителя до адаптації, його рішучість і позитивний імідж стають ключовими факторами успіху в будь-якій сфері його професійної діяльності.

Вчитель, який наближається до ідеалу, також повинен володіти мистецтвом вирішення педагогічних конфліктів. У випадках, коли виникають конфліктні ситуації, вчитель керує їхнім розвитком, втручаючись при потребі та вирішуючи їх. Важливо, щоб вчитель з позиції толерантності глибоко аналізував конфліктну ситуацію і ефективно розв'язував її, а, можливо, навіть запобігав їй. Для цього важливо володіти методичними прийомами, такими як рішучий підхід, компроміс, гумор і інші. При цьому обов'язковими умовами є об'єктивність та аргументованість дій і рішень^[3].

Важливим чинником при формуванні пізнавального інтересу в учнів є і врахування та аналіз вікових особливостей кожного з них. Безперечно, підхід до учнів 5 та 9 класів значно відрізняється, оскільки у силу вікових особливостей для кожного із цієї вікової групи варто підбирати окремі методи та прийоми подачі інформації. Якщо для п’ятикласників більш цікавим методом є гра, то для дев’ятикласників більш прийнятним буде використання методу дискусій чи дебатів. При виборі способу організації освітнього процесу педагогу варто враховувати ці особливості, а також звертати увагу на зацікавленість учнів конкретною темою та розвивати їх пізнавальний інтерес у цьому руслі.

Однією з ключових особливостей учнів у віці від 10 до 15 років є їх перехід на новий рівень інтелектуального та психічного розвитку. Ця зміна проявляється, зокрема, у поступовому переході від конкретного до абстрактного мислення. У цьому віці учні набувають здатності аналізувати, систематизувати та групувати складні явища, виявляти спільність і відмінність між ними.

У зв’язку з цим зміст навчальних предметів в основній школі систематично вибудовується, з явною тематичною спрямованістю, і вводяться нові поняття тощо. Однак, оскільки цей тип мислення знаходиться на етапі становлення, вчителям та авторам навчальних матеріалів слід уникати надмірної теоретизації, і нові поняття рекомендується вводити дозовано та поступово, з опорою на вже відомий учням матеріал^[4].

У старшому шкільному віці учні розвивають навички самоорганізації та самоконтролю, що сприяє їхній здатності самостійно використовувати інформаційно-комунікаційні технології у навчанні.

Мотиви навчання старшокласників часто пов’язані з вибором майбутньої професії, тому вони активно концентруються на предметах і сферах навчання, які будуть важливі для їхньої майбутньої кар’єри. Це призводить до зростання вибірковості уваги та вдосконалення здатності переключати її з одних завдань на інші. Особливу роль відіграє відданість увазі, особливо коли учні цікавляться представленою інформацією. Оцінки втрачають свою вагу, а наголос ставиться на отримання та покращення знань, які будуть корисні для вступу до вищого навчального закладу і подальшої професійної діяльності^[5].

Враховуючи ці особливості вікового розвитку, вчителеві значно легше підібрати методи та засоби організації навчального процесу, що у подальшому робить запам’ятовування та вивчення учнями нового матеріалу більш результативним.

Актуальним у контексті підвищення пізнавального інтересу в учнів є і формування у них мотивації до навчання. Школярі, які зацікавлені у дослідженні історії, мають більш високі показники засвоєння інформації, ніж ті, хто вивчає матеріал через примус.

Стимулювання навчальної діяльності учнів може мати як безпосередню так і опосередковану дію. Це означає, що один і той же стимул може по-різному впливати на учнів, зокрема, на мотиви навчання, в залежності від їх ставлення до цих стимулів, бажання, готовності та прагнення відзиватись на них, від настрою учнів тощо. Тому головним завданням вчителя є створення відповідних умов, що викликали б в учнів відповідну реакцію на стимулювання, тобто перетворили б стимули у відповідні мотиви навчання. Формуючи позитивну мотивацію учнів вчитель не лише розвиває інтерес чи відповідальне ставлення до навчання, але й сприяє формуванню бажання досягати високих результатів та почувати себе успішною особистістю. Це в свою чергу сприяє як підвищенню пізнавальної активності учнів, так і формує відповідні якості особистості. Успіх такої діяльності залежить від індивідуальних особливостей кожного учня та правильно організованої, ефективної роботи вчителя^[6].

Оскільки навчання – це окремий вид діяльності, то і навчальна мотивація є окремим видом мотивації особистості. Як і будь-який інший вид мотивації, навчальна мотивація визначається цілим рядом специфічних для цієї діяльності чинників: освітньою системою, освітньою установою, де здійснюється навчання; організацією навчального процесу (моделлю навчання); суб’єктними особливостями того, хто навчається (вік, стать, інтелектуальний розвиток, здібності, самооцінка, взаємодія з іншими учнями і т. д.); суб’єктними особливостями того, хто навчає і, передусім, системою його ставлення як до учня, так і до справи; специфікою навчального предмету. Мотивація навчання – це система природних, соціальних і особистісних чинників, які спонукають до відвідування навчального закладу, виконання вимог вчителів, включення у процес навчання, до зусиль, необхідних для подолання труднощів, реалізації в процесі навчання власних схильностей, до розвитку здібностей, до навчальної взаємодії^[7].

Отже, можна зробити висновок, що формування цікавості до навчання вимагає уваги до психологічних аспектів, які впливають на мотивацію та сприйняття матеріалу учнями. Педагоги повинні бути готові враховувати ці аспекти, щоб зробити навчання історії більш ефективним і захоплюючим для своїх учнів.

РОЗДІЛ 2

ІННОВАЦІЙНІ ПІДХОДИ ДО ПОДАЧІ МАТЕРІАЛУ НА УРОКАХ МАТЕМАТИКИ

На сучасному етапі розвитку українського суспільства, важливим є перехід освіти на новий рівень, що відповідає міжнародним стандартам та ставить особистість учня в центр освітнього процесу. Особливу увагу слід приділити навчанню математики в школі, орієнтованому на розвиток інтелектуальної сфери особистості учня. Це означає сприяння розвитку пізнавальних інтересів, формування аналітичного мислення та навичок знаходження оптимальних рішень. В умовах сучасної швидкоплинної освіти, соціально-економічний рівень освіти визначається результативністю впровадження інноваційних технологій навчання. Цей процес базується на нових методологічних підходах, сучасних дидактичних принципах та психолого-педагогічних теоріях, які акцентують діяльнісний підхід до навчання в школі.^[8]

Головним завданням вивчення математики в школі є розвиток пізнавальних здібностей, логічного та алгоритмічного мислення, навичок розумової праці, вміння спостерігати та порівнювати, виокремлювати риси схожості та відмінності у порівнюваних об’єктах, виконувати операції аналізу, синтезу, узагальнення, абстрагування та конкретизації. Уроки математики мають бути цікавими, пізнавальними, належним чином організованими та включати активну взаємодію учнів.^[9]

Однією з актуальних методичних проблем в організації освітнього процесу на уроках математики є широке впровадження інноваційних технологій, які часто взяті із-за кордону та не завжди адаптовані до української шкільної практики, що може призводити до погіршення рівня вивчення математики учнями. Важливо враховувати, що вчитель не може уникнути впровадження реформ в освіті, проте він повинен вміти виокремлювати суттєві елементи кожної інновації та адаптувати їх, ґрунтуючись на власному досвіді викладання математики в українських школах. На цьому етапі особливо важливим стає деталізоване вивчення аспектів інновацій та поглиблене розуміння їх структурних елементів, їх ієрархій і взаємозв'язків. Це відкриває можливості для системного підходу до розгляду сутності інновацій у навчанні математики.^[10]

Реалізація інноваційного підходу до навчання учнів ставить перед собою завдання підняти педагогічний процес на новий якісний рівень, підвищити рівень навчальних досягнень та забезпечити психолого-емоційний  комфорт для учнів. Цей підхід сприяє їх подальшій соціальній адаптованості і готовності реалізувати особисті якості в індивідуальній чи колективній діяльності. Важливим результатом є орієнтація на набуття ключових компетентностей: навчальної, культурної, громадянської, соціальної та підприємницької. Сучасна освіта, яка розглядається як система, орієнтована лише на передачу знань та навичок, недостатньо враховує темпи нарощування цих знань у світі.

Сучасна освіта недостатньо розвиває здібності, необхідні випускникам для самостійного визначення в сучасному світі, бути активними та мобільними суб’єктами на ринку праці та приймати обґрунтовані рішення щодо свого майбутнього. Головні недоліки традиційної системи освіти включають в себе несформованість ціннісного ставлення до власного розвитку і освіти, а також відсутність бажання дітей вчитися. Подолання кризи сучасної освіти можливе шляхом інтенсивного реформування з метою створення нової системи загальної освіти, яка поступово замінить традиційну. Важливістю є співіснування традиційної та інноваційної стратегій організації навчання^[11].

Нині справжнім професіоналом у своїй справі може стати лише та людина, яка постійно вчиться, а після отримання диплома здобуває нові знання, вміння, навички, що дають змогу їй адаптуватися до вимог часу, реалізувати свій творчий особистісний потенціал.

Інтеграція України, в європейський освітянський простір вимагає сформованості у педагогів таких ключових компетентностей: вміння здійснювати процеси навчання і виховання; бажання постійно оволодівати новими знаннями з предмета спеціалізації; вдосконалювати зміст навчальних планів і програм залежно від потреб замовників; постійно збагачувати методичний арсенал, вивчаючи напрацьоване і розробляючи інноваційні методики і технології; проводити дослідно-експериментальну роботу, розвивати соціальні та культурні цінності освіти.^[12]

Широкого застосування у шкільній практиці навчання математики набуває такий інноваційний метод як «мейкерство» (від англ. make – «робити»,«створювати») – діяльність, у результаті якої утворюється щось нове або процес створення власноруч певних фізичних об’єктів. Так, створення моделі, розгортки геометричної (стереометричної) фігури значно спрощує розуміння й виконання учнями завдань на обчислення периметру, площі, об’єму. Наприклад, розв’язуючи задачу на кшталт: «Я маю чотирикутник. Як за допомогою мотузки дізнатись, це прямокутник, чи ні?», учні можуть запропонувати виміряти сторони, але це хибна версія. Достатньо пригадати властивість діагоналей прямокутника – і відповідь знайдено. Не виникає сумнівів, що теоретичні факти, підкріпленні практичними діями, краще засвоюються, тому необхідно розвивати у школярів мейкерські здібності, залучати учнів до мейкерства як на уроках, так і в позаурочний час,що сприяє підвищенню пізнавального інтересу до вивчення математики.^[13]

Щодо педагогічного процесу, інновації передбачають впровадження нового підходу до цілей, змісту, методів і форм навчання та виховання, а також спільну діяльність вчителя та учня на уроці математики. В літературі з педагогіки існує безліч класифікацій і груп інновацій. Серед найвідоміших виділяють інновації, спрямовані на створення нових форм, технологій і методів навчально-виховного процесу, а також ті, які спрямовані на розробку нового змісту освіти та нових способів його структурування.

Традиційно освітній процес орієнтований на передачу та творче освоєння знань. Сучасна освіта, однак, ставить перед собою завдання не лише формування носіїв інформації, але й всебічного розвитку особистості. Процес вивчення математики, так само як і будь-якого іншого предмету, повинен вирішувати освітні, виховні та розвиваючі завдання.^[14]

Застосування інтерактивних технологій вимагає від учителя і учнів ретельної підготовки. Важливо, щоб вони володіли навичками ефективного спілкування, використовували активне слухання, висловлювали особисті думки, критично ставилися до інформації, вміли ставити запитання і відповідати на них. Успішність інтерактивних технологій залежить від уміння вчителя: висувати завдання для попередньої підготовки, які стимулюють учнів вивчати матеріал перед заняттям; обирати для уроку або заняття вправи, що дозволяють учням легко освоювати тему; вживати інтерактивні вправи, які сприяють глибокому розумінню матеріалу; надавати час учням для ретельного розгляду завдань і серйозного їх вирішення; обмежувати кількість інтерактивних вправ на одному занятті; вести обговорення результатів інтерактивної діяльності з акцентом на додатковому матеріалі теми, не охопленому в ході інтерактивних вправ; застосовувати швидкі опитування та самостійні домашні роботи з різноманітних матеріалів теми, що не входили в інтерактивні завдання.^[15]

До інтерактивних методів навчання О. Пометун відносить ротаційні трійки, карусель, навчаючи – учусь, акваріум, ажурна пилка, симуляційні або імітаційні ігри, ПРЕС, дерево рішень, займи позицію тощо.

Наприклад, можна використовувати на уроках алгебри ресурс learningapps при вивченні багатьох тем з курсу алгебри 7 клас. Завдання вчитель може формулювати на свій розсуд: самостійна робота учнів, перевірка вивченої теми, групова робота класу тощо.

Вивчаючи тему «Одночлени» можна запропонувати учням таке завдання: «серед виразів вибрати лише ті, що є одночленами». Таке завдання допоможе дітям краще усвідомити, які вирази є одночленами, а які ні.^[16]

Отже, можна стверджувати, що інноваційні підходи до вивчення математики визначають суттєві зміни в освітньому процесі, спрямовані на поліпшення якості освіти. Залучення сучасних технологій, таких як використання комп’ютерних програм та інтерактивних платформ, сприяє ефективнішому засвоєнню матеріалу та стимулює інтерес до предмету. Особлива увага приділяється розвитку критичного мислення учнів, що сприяє їхньому глибшому розумінню математичних концепцій. Інновації в навчанні математики сприяють створенню стимулюючого та підтримуючого середовища, сприяючи підвищенню якості освіти та розвитку ключових навичок учнів.

РОЗДІЛ 3

ОРГАНІЗАЦІЯ МАТЕМАТИЧНИХ ЗАХОДІВ ЯК ІНСТРУМЕНТ ФОРМУВАННЯ В УЧНІВ ЗАЦІКАВЛЕНОСТІ ДО ВИВЧЕННЯ ПРЕДМЕТУ

Одне з найактуальніших завдань освітнього процесу в закладах освіти – навчити здобувача освіти вчитися, вміти самостійно здобувати знання. Зважаючи на це, можна стверджувати, що самостійна пізнавальна діяльність є однією із найважливіших складових освітнього процесу.

Теоретичний аналіз психолого-педагогічної й методичної літератури засвідчує, що самостійна пізнавальна діяльність учнів – це діяльність, що полягає у визначенні (самостійному або за допомогою вчителя) мети, завдань, проблеми на основі пізнавальних потреб та інтересів, мотивів, вибору власного пізнавального шляху, спрямованого на самостійне розв’язання поставлених завдань.

Під організацією самостійної пізнавальної діяльності ми розуміємо відбір засобів, форм і методів, які стимулюють пізнавальну активність і самостійність, їх реалізацію та забезпечення умов ефективності. Таким чином, здійснюючи відбір видів самостійної пізнавальної діяльності, відповідних методів, форм і засобів, необхідно враховувати мету та завдання вивчення матеріалу, його специфіку. Важливим елементом системи організації самостійної пізнавальної діяльності учнів є позакласна робота, яка повинна бути логічним продовженням навчальної роботи на уроці. Під час організації самостійної пізнавальної діяльності учнів слід обов’язково ураховувати принципи диференціації й індивідуалізації навчання, використання сучасних інформаційних технологій та інноваційних методик навчання.^[17]

Один з ефективних методів залучення учнів до математики полягає у ретельно продуманій організації позакласної роботи (на скільки вона можлива в умовах сьогодення). Такий підхід спрямований на досягнення різноманітних навчальних та виховних цілей, таких як пробудження і розвиток інтересу до математики, розширення та поглиблення знань з програмового матеріалу, розвиток математичних здібностей, формування науково-дослідницьких навичок, культури математичного мислення та інше.

Особливий акцент слід зробити на використанні історичного матеріалу, оскільки він відіграє ключову роль у формуванні уявлень учнів про математику як невід’ємну складову загальнолюдської культури. Історичний контекст допомагає учням зрозуміти практичне застосування математичних концепцій у техніці та повсякденному житті. Крім того, вивчення історії математики стимулює науковий підхід та надає можливість краще зрозуміти сучасний стан математичної науки.^[18]

Позакласні заняття з математики є невід’ємною складовою навчально-виховної роботи та допомагають досягти різноманітних цілей. З опитувань вчителів видно, що така робота часто має епізодичний характер, і не всі вчителі повністю усвідомлюють її значення. Проте, важливо визначити позитивні сторони цього підходу.

По-перше, відзначається тим, що позакласні заняття можуть бути спрямовані на використання ігор, розваг та змагань, що надає вчителю великий простір для творчості. Вони не обмежені програмою і дозволяють вчителю підбирати завдання, що відповідають рівню знань та умінь учнів, і здійснювати індивідуальний підхід.

По-друге, завдання на позакласних заняттях мають проблемний характер, розкривають цікаві аспекти математики, пов’язані з реальним життям, трудовою діяльністю, і спрямовані на вирішення ситуацій, що ставляться перед учнями у повсякденному житті.

По-третє, такі заняття організовані у формі груп, які утворюються на добровільній основі. Це дозволяє об’єднувати учнів з різних класів і створювати сприятливе середовище для взаємодії та обміну досвідом.

По-четверте, враховуючи психофізичні особливості учнів, вчителі організовують заняття так, щоб матеріал був доступний та сприяв розвитку самостійності та ініціативності учасників, застосовуючи нестандартні прийоми та форми роботи.

По-п’яте, тривалість позакласних занять необмежена і може варіюватися від кількох хвилин до 45 хвилин, що дозволяє вчителям гнучко планувати інтерактивні вправи та завдання.^[19]

Участь у позакласній роботі є добровільною і не оцінюється балами, що робить її доступною для учнів різного рівня математичних здібностей. Це дозволяє залучати до неї дітей з різними індивідуально-психологічними особливостями та реалізовувати особистісно орієнтований підхід. Врахування потреб, мотивів, здібностей, активності, інтелекту кожного учня сприяє формуванню індивідуального підходу до навчання та розвитку.

Зокрема, обдарованих учнів до математики слід стимулювати до активної участі в гуртковій роботі, олімпіадах та конкурсах, де вони можуть розкрити свій потенціал та демонструвати здатність розв'язувати нестандартні задачі. Вчителю важливо вчасно виявляти обдарованих дітей та систематично розвивати їхні здібності, створюючи умови для стійкого інтересу до математики.

Згадано, що в ранньому шкільному віці іноді важко розпізнати математичні здібності. Тому важливо залучати всіх учнів до позакласної роботи, щоб кожний мав можливість розкрити свій потенціал. Учням, яким важко дається математика, можна пропонувати участь у різноманітних колективних заходах, таких як математичні ранки, екскурсії, ігри, вікторини, де вони матимуть можливість не лише весело провести час, але й почерпнути нові знання та розкрити цікавість до предмету.

Важливо, щоб вчитель володів майстерністю та педагогічним тактом, створюючи сприятливий клімат для навчання математики для всіх учнів, допомагаючи кожній дитині вірити у власні сили та відкривати світ цікавої математики.^[20]

Реалізація ігрових прийомів і ситуацій у визначеній формі занять відбувається за такими основними напрямками:

                   дидактична мета ставиться перед учнями у формі ігрового завдання;

                   навчальна діяльність підкоряється правилам гри;

                   навчальний матеріал використовується як її засіб;

                   у навчальну діяльність уводиться елемент змагання, що переводить дидактичне завдання в ігрове;

                   успішне виконання дидактичного завдання пов’язується з ігровим результатом.^[21]

Факультативні заняття в математиці виступають як важливий елемент позакласної роботи, спрямованої на поглиблення та розширення знань учнів. Цей вид роботи відрізняється від звичайних уроків тим, що його мета — не просто підвищення оцінок, а розгляд проблемного матеріалу, розв’язування складних завдань, проведення цікавих дискусій. Важливо, щоб факультативи були цікавими та захоплюючими для учнів, стимулювали їхній інтерес до математики та розвивали критичне мислення.

Математичні гуртки є ще однією важливою формою позакласної роботи, де учні можуть розширювати свої знання та навички, виходячи за межі навчальної програми. Ці гуртки створюють можливість для поглибленого вивчення математики, вирішення складних задач, розвитку креативності та самостійності в опрацюванні матеріалу. Вони можуть включати в себе різноманітні види діяльності, такі як розв'язування головоломок, вивчення нових тем, математичні ігри та експерименти.

Важливо, щоб вчителі, які проводять позакласну роботу, добре планували кожне заняття, створюючи цікаві та доступні завдання, які стимулюватимуть учнів до активності та розвитку їхніх математичних здібностей.^[22]

Отже, можна зазначити, що організація математичних заходів в шкільному середовищі є ефективним інструментом для підвищення інтересу учнів до математики. Проведення таких заходів дозволяє перенести вивчення математики з формального контексту у веселий та захопливий формат, що сприяє активній участі учнів та розвитку їхнього інтересу. Спеціальні математичні конкурси, ігри, вікторини та проекти допомагають зробити математику більш доступною та заохочують учнів застосовувати свої знання у практичних ситуаціях. Завдяки цим заходам формується позитивне ставлення до математики, розвиваються комунікативні навички та збагачується освітній процес. Такий підхід сприяє підвищенню якості вивчення математики та формуванню позитивного ставлення учнів до даного предмету.

РОЗДІЛ 4

РОЗВИВАЛЬНІ ІГРИ ТА ВИКОРИСТАННЯ МАТЕМАТИКИ У РЕАЛЬНОМУ ЖИТТІ: ПРИНЦИПИ ТА УМОВИ РЕАЛІЗАЦІЇ

За словами В.О.Сухомлинського гра – це шлях до освіченості дитини, вікно у розумовий і духовний світ підлітка. Не використовуючи методи гри ми позбавляємо себе і учнів допитливості і цікавості в нашому предметі. Розвивальні ігри поєднують у собі як виховання учнів, так і навчання. При їх реалізації на уроці ми розширюємо коло інформації, де школярі зацікавлюються темою уроку, починають розвивати свій інтелект. Якщо порівняти подачу матеріалу від серйозного викладу сухого тексту і цікавої захоплюючої гри, ми матимемо зовсім різні результати, адже ще з дитинства гра розслаблює, стимулює зниження психічного навантаження, й саме це дає поштовх до реалізації мети уроку.

Розвивальні ігри допомагають в процесі навчання як форма вивчення матеріалу, так і засіб закріплення знань. Головна ціль таких ігор – досягнення мети уроку.^[23]

Розвивальне навчання в математиці спрямоване на формування не лише знань та навичок, але й розвиток критичного та творчого мислення учнів. Основна ідея полягає в тому, щоб вчити учнів самостійно мислити, розв'язувати проблеми та застосовувати математичні знання в різних ситуаціях.

Однією з ключових цілей розвивального навчання в математиці є створення атмосфери, що сприяє активному взаємодії між учителем та учнями, а також між самими учнями. Це допомагає створити учням внутрішню мотивацію до навчання та розвитку, а також сприяє формуванню творчого підходу до вирішення математичних задач.

Важливою складовою розвивального навчання є використання різноманітних методів та форм роботи, таких як групова робота, проекти, дослідження, вирішення проблем, дискусії тощо. Це дозволяє учням розвивати комунікативні навички, навички роботи в колективі, а також вчити їх застосовувати математичні знання в реальних ситуаціях.

Застосування принципів розвивального навчання в математиці важливо не лише для формування глибокого розуміння предмету, але і для розвитку творчих та критичних мисленнєвих навичок, які є важливими в сучасному інформаційному суспільстві.^[24]

Для реалізації розвивальної функції навчання при вивченні математики необхідно врахувати методичні вимоги до змісту, методів, організаційних форм та засобів навчання. До основних методичних вимог щодо змісту навчання варто віднести такі: зменшення обсягу громіздких обчислень та перетворень; посилення неперервності, функціональності змісту навчання; персоніфікований виклад матеріалу, тобто аналіз, де можливо, математичних фактів в аспекті їх історичного становлення і розвитку; орієнтація на матеріал, який передбачає перебудову знайомих способів розв’язування, доведення, дослідження; вибір із багатьох варіантів раціонального; використання матеріалу, що передбачає відкриття нових причинно-наслідкових зв’язків, закономірностей, загальних правил розв’язування цілого класу задач; структурування навчального матеріалу, подача його “великими порціями” . Зміст навчання має бути впорядкований таким чином, щоб його частина була ущільнена і зведена до єдиної логічної основи, здійснюватись ідея укрупнення дидактичних одиниць, ідея розгортання і згортання навчального матеріалу за допомогою опорних схем і сигналів.^[25]

Особливостями уроків математики в розвивальному навчанні є:

                   задачний підхід до організації навчально-математичної діяльності учнів;

                   створення ситуацій успіху та розв’язання проблемних задачних ситуацій;

                   висвітлення прикладної й практичної ролі математики, розв’язання проблеми походження теоретичних знань;

                   поєднання методів математичного і навчального (навчально-теоретичного) моделювання;

                   вивчення програмного матеріалу згідно з логікою сходження від абстрактного (загального) до конкретного (часткового);

                   стильовий підхід до організації процесу учіння (реалізація технології формування персональних пізнавальних стилів і навчальних стратегій);

                   відмова від традиційної установки на «готові» знання та способи дій в умовах суб’єкт-суб’єктних і міжособистісних відносин;

                   первинні колективні, колективно розподілені форми (групові, парні) навчальної роботи і вторинні – індивідуальні;

                   рефлексія навчально-математичної діяльності (процеси учіння математики) та особистісного розвитку.^[26]

В цілому можна констатувати, що урок, зберігши властиві йому ознаки, в той же час є нині не тільки варіативною, але і постійно розвивальною  формою організації колективно-індивідуального навчання математики. У свою чергу, урок математики має цілу низку специфічних особливостей. Для нього характерні і є найбільш істотними такі ознаки:

                   зміст уроку математики, як правило, не є автономним, він розгортається з опорою на раніше вивчене, готуючи базу для засвоєння нових знань, що пов’язані з суворою логікою побудови курсу математики;

                   у процесі опанування  складною системою математичних знань зазвичай відбувається істотний поділ учнів за здібностями, тому необхідно здійснювати на уроках математики диференціацію в навчанні, розвитку логічного мислення,формування самоконтролю в учнів тощо;

                   при навчанні математики повинні бути створені умови для того, щоб кожен учень міг засвоїти на уроці головне в досліджуваному матеріалі, оскільки без базової математичної підготовки неможлива постановка освіти сучасної людини;

                   прагнення до ефективного навчання учнів на уроках математики обумовлено і тим, що в школі математика служить опорним предметом для вивчення суміжних дисциплін;

                   у процесі навчання математики теоретичний матеріал усвідомлюється і засвоюється переважно в процесі розв’язування завдань, тому на уроках математики найчастіше теорія не вивчається без практики.^[27]

Математика має широке практичне застосування у сучасному житті та є необхідною для розв’язання різноманітних завдань, серед яких:

                   Управління особистими фінансами вимагає математичних навичок для розрахунків бюджету, розподілу коштів, розрахунку процентів за кредитами, інвестування та пенсійного планування.

                   Економічні моделі, прогнозування та аналіз даних є невід’ємною частиною сучасної економіки. Математика допомагає вивчати ринкові тенденції, раціоналізувати виробництво та приймати ефективні управлінські рішення.

                   Криптографія, комп’ютерна графіка, оптимізація алгоритмів – усе це базується на математичних концепціях. Математика є основою для розробки програмного забезпечення та комп’ютерних технологій.

                   В медичних дослідженнях використовуються статистичні методи для аналізу результатів клінічних випробувань, алгоритми обробки зображень для діагностики та математичне моделювання для розробки нових методів лікування.

                   Математика відіграє важливу роль у визначенні оптимальних маршрутів, плануванні розкладів транспортних засобів, управлінні логістикою та вирішенні завдань оптимізації.

                   Математика є мовою, яка описує фізичні явища, хімічні реакції та багато інших аспектів наукових досліджень. Вона використовується для побудови моделей та передбачення результатів досліджень.

                   В розрахунках та дизайні енергетичних систем (сонячних батарей, вітряних турбін, ядерних реакторів) математика грає ключову роль. Також вона використовується для ефективного управління споживанням електроенергії.

                   Фізика, хімія та інші точні науки неможливі без математичних інструментів. Математика служить мовою опису природних законів.

Ці приклади демонструють, наскільки математика широко використовується в різних сферах сучасного життя і як важлива її роль у вирішенні практичних завдань та проблем.

Отже, можна зазначити, що застосування розвивальних ігор та математичних концепцій у реальному житті є значущим елементом в навчальному процесі, спрямованим на глибоке розуміння та практичне використання математики. Розвивальні  ігри сприяють активному залученню учнів, розвитку їхньої логіки, творчого мислення та сприйняття математичних концепцій. Застосування математики в реальних сценаріях розкриває її прикладну цінність, створюючи зв'язок між теорією та практикою. Такий підхід сприяє формуванню навичок критичного мислення, розв’язанню життєвих завдань та розумінню важливості математики в різних аспектах повсякденного життя. В цілому, комбінація розвивальних ігор та практичного застосування математики покращує якість навчання, стимулює інтерес до предмету та сприяє глибшому засвоєнню математичних знань.

РОЗДІЛ 5

МЕТОДИЧНИЙ МАТЕРІАЛ З МАТЕМАТИКИ ДЛЯ САМОСТІЙНОГО ОПРАЦЮВАННЯ

Вивчення математики є захоплюючим та важливим етапом освітнього шляху, який розвиває аналітичне мислення, логіку та навички вирішення складних завдань. Щоб надати учням додаткові засоби для самостійного опрацювання математичних концепцій, цей методичний матеріал створено з урахуванням потреб самоосвіти. Він спрямований на поглиблене вивчення різноманітних тем, від базових до більш складних, надаючи чіткі пояснення, приклади та завдання для самостійного вирішення. Розвиваючи не лише конкретні математичні навички, але й загальний рівень розуміння предмету, цей методичний матеріал сприяє формуванню впевненості в власних здібностях та стимулює бажання вдосконалювати свої знання.

Наприклад, можна продемонструвати школярам математичний фокус, а потім разом розібратися, магія це чи математика, та за яким принципом працює.

Приклад математичного фокуса: Попросіть учнів загадати будь-яке число та виконати три дії нескладних обчислень, після чого ви вгадаєте результат. Спершу учням потрібно подумки загадати число, потім помножити його на 2, після цього додати до результату 8. Суму розділити на 2 та відняти задумане число. Принцип фокусу можна формалізувати наступним чином:

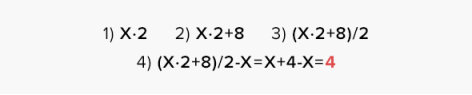
Тож по факту виходить, яке б число не задумали учні, у результаті математичних обчислень у всіх вийде однаковий результат – 4.

Ось кілька цікавих задач на вартість життя:

Задача 1:

Сім'я витрачає 30% свого доходу на оплату житла, 20% - на їжу, 15% - на транспорт, 10% - на освіту та 25% - на інші потреби. Яка частина доходу сім'ї йде на їжу, і скільки це становить в грошовому еквіваленті, якщо їхній дохід складає 15000 гривень?

Задача 2:

Оплата комунальних послуг для одного жителя у місті А становить 35% від його місячного доходу, в той час як у місті Б ця послуга складає 25%. Якщо місячний дохід обох мешканців    по  12000 гривень, то скільки витрачає  мешканець міста Б на комунальні послуги?

Задача 3:

Магазин пропонує знижку на продукти харчування в розмірі 20%. Якщо покупець купує продукти на суму 600 гривень, скільки гривень він зекономить завдяки цій знижці?

Задача 4:

Сім'я складається з трьох членів: батька, матері та двох дітей. Щомісяця сім'я витрачає 40% свого доходу на оплату житла, 25% - на їжу, 15% - на транспорт, а решту грошей вони використовують на освіту та розваги. Яка вартість життя для цієї сім'ї, якщо їхній щомісячний дохід становить 25000 гривень?

Задача 5:

Мешканець міста витрачає 30% свого місячного доходу на оренду житла, 20% - на продукти, 15% - на комунальні послуги, а решту грошей він розподіляє між розвагами та накопиченням. Яка вартість життя для цього мешканця, якщо його щомісячний дохід складає 20000 гривень?

Задача 6:

Дитина витрачає 40% своїх щотижневих кишенькових грошей на розваги, 30% - на книги, а решту - на смаколики. Яка вартість тижневих розваг для дитини, якщо її кишенькові гроші на тиждень  становлять 300 гривень?

Ці задачі розвиватимуть у дітей навички рахунку та фінансової грамотності у повсякденному житті.

Також вашим учням неодмінно сподобаються творчі задачі, для розв’язання яких доведеться проявити кмітливість та логічне мислення.

Багато учнів цікавляться оригамі. Однак мало, хто замислюється, що в основі цього мистецтва лежать математичні закономірності. Пропоную разом скласти цікаву фігурку та проаналізувати, як можна, наприклад, формалізувати процес її створення.

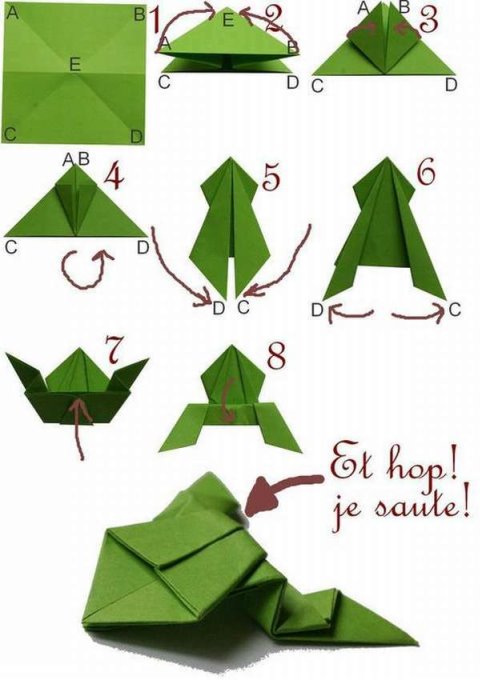
Техніка оригамі (мистецтво виготовлення фігур з паперу шляхом складання) може бути застосована в математиці для вивчення різних математичних концепцій. Ось кілька прикладів, які я також використовую на своїх уроках:

1.               Геометрія:
   1.               Квадрати та прямокутники: З використанням техніки оригамі можна легко створити квадрати та прямокутники, вивчаючи їхні властивості, такі як площа та периметр.
2.               Алгебра:
   1.               Графічне представлення виразів: За допомогою оригамі можна створювати графічні представлення алгебраїчних виразів, що допомагає візуалізувати алгебраїчні концепції.
   2.               Геометричні тіла:Куби та паралелепіпеди: Оригамі може бути використане для створення тривимірних геометричних тіл, таких як куби та паралелепіпеди.
   3.               Рівності та нерівності: Оригамі може бути використане для демонстрації математичних відносин, таких як рівності та нерівності, через різноманітні складання.
3.               Комбінаторика:
   1.               Поєднання та перестановки: Створюючи оригамі фігури, можна досліджувати комбінаторні концепції, такі як різні способи складання та розгортання.
   2.               Математичні головоломки:Задачі на логіку та обчислення: Оригамі може бути використане для створення математичних головоломок та завдань на розвиток логічного мислення.
   3.               Теорія чисел:Множення та ділення: Створення оригамі з можливістю складати та розгортати фігури може допомагати у вивченні операцій множення та ділення.
4.               Геометричні перетворення:
   1.               Відображення та обертання: Оригамі може слугувати інструментом для вивчення геометричних перетворень, таких як відображення та обертання.

Застосування техніки оригамі у математиці робить вивчення більш інтерактивним та забезпечує візуальне представлення абстрактних математичних концепцій.

Використання оригамі у задачах на логіку:

Задача 1: Логічне висловлення

Уявімо, що у вас є оригамі-квадрат, складений з паперу двох різних кольорів. Якщо одна половина квадрата синього кольору, а інша половина – червоного, то який колір буде зверху, коли ви його розкриєте?

a) Синій

b) Червоний

c) Залежить від того, як ви його склали

d) Зелений

Задача 2: Логічний лабіринт

Розгляньте оригамі вигляду лабіринту. Щоб вийти з лабіринту, потрібно розгорнути його. Якщо ми розглядаємо входом одну сторону квадрата, а виходом – іншу, як потрібно скласти лабіринт, щоб він був прохідним?

a) Поміняти місцями входи та виходи

b) Повернути лабіринт на 180 градусів

c) Зігнути його в середині

d) Закрити виходи

Задача 3: Логічні комбінації

Уявімо, що ви маєте оригамі, яке можна скласти двома різними способами. Якщо вибрати один спосіб, то на фінальній фігурі буде зображено зірку. Якщо інший спосіб, то коло. Яка фігура буде зображена на фінальній фігурі, якщо вибрати обидва способи одночасно?

a) Коло та зірка

b) Тільки коло

c) Тільки зірка

d) Четверта форма

Задача 4: Логічна перестановка

Ваше оригамі має форму трикутника, і ви можете його скласти так, щоб вершина трикутника була знизу або зверху. Якщо ви його складаєте так, щоб вершина була знизу, то якою буде фінальна форма?

a) Трикутник

b) Квадрат

c) Коло

d) Інший трикутник

Задача 5: Логічні операції

Уявімо, що ви маєте дві квадратні аркуші паперу, з яких можна скласти орігамі. Якщо обидва аркуші одного кольору, то ви складаєте їх так, щоб отримати зірку. Якщо різного кольору, то складаєте так, щоб отримати квадрат. Що ви отримаєте, якщо ви використовуєте один червоний та один зелений аркуш?

a) Зірку

b) Квадрат

c) Трикутник

d) Коло

Ці задачі допомагають нам розвивати логічне мислення, уважність та креативність через застосування техніки оригамі.

ВИСНОВКИ

Зацікавленість сучасних учнів математикою має велике значення з численних причин:

1.               Вивчення математики розвиває аналітичні та логічні навички. Вміння вирішувати математичні завдання формує критичне мислення та здатність аргументувати власні висновки.
2.               Багато сучасних професій вимагають від працівників високий рівень математичної грамотності. Вивчення математики допомагає формувати навички, які є цінними на ринку праці, такі як аналіз даних, програмування та розв'язання складних завдань.
3.               Багато інновацій та технологічних досягнень базуються на математичних концепціях. Зацікавленість учнів математикою сприяє їхньому більш ефективному вивченню та використанню сучасних технологій.
4.               Математика може бути захопливою і творчою сферою. Розвиваючи математичне мислення, учні вчаться творчо підходити до розв'язання завдань та стимулювати свій інтелект.
5.               Навички, отримані при вивченні математики, є необхідним елементом загального освітнього фундаменту. Вони допомагають учням легше розуміти та адаптуватися до різних наукових, технічних та гуманітарних предметів.
6.               Зацікавленість математикою може допомагати подолати математичний стрес, який може виникнути внаслідок негативного досвіду або невпевненості.
7.               Математика вчить систематичності, терпіння та самодисципліни. Розвиваючи ці навички, учні можуть досягати більших успіхів не лише в навчанні, але й у різних аспектах свого життя.

Загалом, зацікавленість математикою не лише робить процес навчання привабливим, але і готує учнів до подальших викликів і можливостей у сучасному світі.

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

1.               Андрущенко В. Формування особистості вчителя в сучасних умовах. Політичний менеджмент. 2005. № 1. С. 58–69. URL: http://www.irbis-nbuv.gov.ua/cgi-bin/irbis_nbuv/cgiirbis_64.exe?C21COM=2&I21DBN=UJRN&P21DBN=UJRN&IMAGE_FILE_DOWNLOAD=1&Image_file_name=PDF/PoMe_2005_1_9.pdf.
2.               Барабаш І. Використання інноваційних технологій на уроках математики. Сучасний рух науки: тези доп. XI міжнародної науково-практичної інтернет-конференції, 8-9 жовтня 2020 р. Дніпро, 2020. Т.1. С. 42–43. URL: http://dspace.puet.edu.ua/bitstream/123456789/10005/1/11th%20Conference%20Part%201.pdf#page=42.
3.               Білик Т. Інтеграція інноваційних елементів та інтерактивних технологій на уроках математики в початковій школі. Сучасні інформаційні технології та інноваційні методики навчання в підготовці фахівців: методологія, теорія, досвід, проблеми. 2021. Вип. 61. С. 100–108. URL: https://vspu.net/sit/index.php/sit/article/view/3026.
4.               Буйницька О. Цікавість як засіб підвищення ефективності навчання фізики. Фізика і астрономія в школі. 2007. № 1. С. 24–35.
5.               Войненко К. Позакласна робота з математики як засіб розвитку математичних здібностей молодших школярів. Сучасні технології формування логіко-математичної компетентності в дітей дошкільного та молодшого шкільного віку / за заг. ред. Н. П. Тарнавської., Н. Ю. Рудницької, Ю. М. Мурашевич Житомир: ФОП «Левковець», 2015. С. 87. URL: http://eprints.zu.edu.ua/23991/1/14.PDF.
6.               Годованюк Т. Позакласна робота з математики. Методика, освіта, пошук. 2011. С. 19–24. URL: https://dspace.udpu.edu.ua/bitstream/6789/547/1/%D0%93%D0%9E%D0%94%D0%9E%D0%92%D0%90%D0%9D%D0%AE%D0%9A_6.pdf.
7.               Голодюк Л. Формування навчально-дослідницьких умінь учнів на уроках математики. Наукові записки. 2015. Вип. 7. С. 32–38. URL: http://www.irbis-nbuv.gov.ua/cgi-bin/irbis_nbuv/cgiirbis_64.exe?C21COM=2&I21DBN=UJRN&P21DBN=UJRN&IMAGE_FILE_DOWNLOAD=1&Image_file_name=PDF/nz_pmfm_2015_7(3)__8.pdf.
8.               Дзюбко Л., Гриценок Л. Мотивація навчальної діяльності як психолого-педагогічна проблема. Психолінгвістика. 2009. Вип. 4. С. 33–43. URL: http://www.irbis-nbuv.gov.ua/cgi-bin/irbis_nbuv/cgiirbis_64.exe?C21COM=2&I21DBN=UJRN&P21DBN=UJRN&IMAGE_FILE_DOWNLOAD=1&Image_file_name=PDF/psling_2009_4_5.pdf.
9.               Дичківська І.М. Інноваційні педагогічні технології: Навчальний посібник. К.: Академ.видав., 2004. 352 с.
10.          Докучина Т. Мотивація навчання як запорука стимулювання учнів до досягнення успіху. Педагогічна освіта: теорія і практика. 2011. Вип. 8. С. 32–37. URL: http://www.irbis-nbuv.gov.ua/cgi-bin/irbis_nbuv/cgiirbis_64.exe?C21COM=2&I21DBN=UJRN&P21DBN=UJRN&IMAGE_FILE_DOWNLOAD=1&Image_file_name=PDF/znppo_2011_8_7.pdf
11.          Жерновникова О. Особливості сучасного уроку математики. Педагогіка і психологія. 2013. Вип. 43. С. 27–33. URL: http://www.irbis-nbuv.gov.ua/cgi-bin/irbis_nbuv/cgiirbis_64.exe?C21COM=2&I21DBN=UJRN&P21DBN=UJRN&IMAGE_FILE_DOWNLOAD=1&Image_file_name=PDF/znpkhnpu_ped_2013_43_7.pdf.
12.          Жигайло О. Використання інноваційних технологій у позакласній роботі з математики вчителями початкових класів. Збірник наукових праць Херсонського державного університету. 2016. Вип. 74 (1). С. 114–119. URL: http://www.irbis-nbuv.gov.ua/cgi-bin/irbis_nbuv/cgiirbis_64.exe?C21COM=2&I21DBN=UJRN&P21DBN=UJRN&IMAGE_FILE_DOWNLOAD=1&Image_file_name=PDF/znppn_2016_74(1)__25.pdf.
13.          Жидецька О., Григор’єва Т. Урахування вікових особливостей учнів старшої школи під час викладання іноземної мови. Теорія і методика навчання і виховання. 2020. С. 16–18. URL: http://eprints.zu.edu.ua/31296/1/%D0%96%D0%B8%D0%B4%D0%B5%D1%86%D1%8C%D0%BA%D0%B0%20%D0%9E.%D0%9E._%D0%A2%D0%B5%D0%B7%D0%B8%202%28%D1%80%D0%BE%D0%B7%D0%B4%D1%96%D0%BB%201.3%29.pdf.
14.          Ковтонюк Г. Роль позакласних заходів в організації самостійної пізнавальної діяльності школярів з математики та фізики. Нова педагогічна думка. 2016. № 2 (86). С. 66–68. URL: https://library.vspu.net/jspui/bitstream/123456789/3397/1/%D0%9A%D0%9E%D0%92%D0%A2%D0%9E%D0%9D%D0%AE%D0%9A%20%D0%93%D0%9C_2016_%D0%BD%D0%BE%D0%B2%D0%B0%20%D0%BF%D0%B5%D0%B4%20%D0%B4%D1%83%D0%BC%D0%BA%D0%B0_%D1%80%D1%96%D0%B2%D0%BD%D0%B5.pdf.
15.          Коршун Ю. Роль алгебраїчного апарату у розвиваючих іграх. Магістерські студії. Альманах / ред. кол. : Д. С. Мальчикова, Т. С. Корнішева. Херсон ; Івано-Франківськ : ХДУ, 2023. Вип. 23. С. 510–514. URL: http://ekhsuir.kspu.edu/handle/123456789/18710.
16.          Кукуєва А. Позакласна робота з математики в старшій школі. Наукові записки молодих учених. 2019. № 3. С. 75. URL: https://phm.cuspu.edu.ua/ojs/index.php/SNYS/article/view/1602/pdf.
17.          Лимар Ю., Чекан Ю. Нові професійні ролі вчителя в умовах Нової української школи. Інноваційна педагогіка. 2019. Вип. 15. Т. 2. С. 100–103. URL: https://dspace.chnpu.edu.ua/jspui/handle/123456789/780.
18.          Назаренко І. Елементи розвиваючого навчання на уроках математики у 5-6 класах. Збірник наукових праць викладачів, аспірантів, магістрантів і студентів фізико-математичного факультету (до 100-річчя від дня народження Миколи Федоровича Гур’єва). Полтава: АСМІ, 2010. С. 104–105. URL: http://dspace.pnpu.edu.ua/bitstream/123456789/3965/1/fakultet2010.pdf#page=104.
19.          Орел Л. Позакласна робота з математики як засіб розвитку математичних здібностей молодших школярів. Вісник Житомирського державного університету ім. І. Франка. 2005. Вип. 24. С. 254–257. URL: http://eprints.zu.edu.ua/3776/1/05olomsh.pdf.
20.          Пасічник О. Вікові особливості учнів 5-6-х класів та їх вплив на добір змісту навчання іноземних мов. Проблеми сучасного підручника. 2020. Вип. 25. С. 88–102. URL: https://ipvid.org.ua/index.php/psp/article/view/57/56.
21.          Полякова О. Інноваційна освітня діяльність вчителя початкових класів на уроках математики. Інноваційна діяльність педагога в умовах реформування шкільної освіти. 2015. С. 23. URL: https://elibrary.kubg.edu.ua/id/eprint/12303/1/O_Polyakova_IDPvURSCHO_IPPO.pdf.
22.          Семенець С. Аспекти реалізації розвиваючої функції навчання при вивченні математики. Національна освіта: традиції та новації у контексті ідей І. Огієнка. 2002. С. 178–180. URL: http://eprints.zu.edu.ua/19895/1/Semenets_Aspekty_realizatsii_rozvyvayuchoji_funktsiji.pdf.
23.          Сірант Н., Кисіль Н. Інноваційні технології навчання на уроках математики в початковій школі. URL: https://pedcollege.lnu.edu.ua/wp-content/uploads/2015/09/%D0%86%D0%9D%D0%9D%D0%9E%D0%92%D0%90%D0%A6%D0%86%D0%99%D0%9D%D0%86-%D0%A2%D0%95%D0%A5%D0%9D%D0%9E%D0%9B%D0%9E%D0%93%D0%86%D0%87-%D0%9D%D0%90%D0%92%D0%A7%D0%90%D0%9D%D0%9D%D0%AF-%D0%9D%D0%90-%D0%A3%D0%A0%D0%9E%D0%9A%D0%90%D0%A5-%D0%9C%D0%90%D0%A2%D0%95%D0%9C%D0%90%D0%A2%D0%98%D0%9A%D0%98-%D0%92-%D0%9F%D0%9E%D0%A7%D0%90%D0%A2%D0%9A%D0%9E%D0%92%D0%86%D0%99-%D0%A8%D0%9A%D0%9E%D0%9B%D0%86.pdf.
24.          Ткач К., Гоменюк Г. Інтерактивні методи навчання на уроках математики з використанням ІКТ. Сучасні цифрові технології та інноваційні методики навчання: досвід, тенденції, перспективи. 2022. № 9. С. 184–187. URL: http://dspace.tnpu.edu.ua/bitstream/123456789/27599/3/Tkach_Gomenuk.pdf.
25.          Толок Д., Дейніченко Т. Інноваційні форми і методи в навчанні математики. Інноваційні педагогічні технології в цифровій школі : тез доп. учасників IV Всеукр. (з міжнар. участю) наук.-практ. конф. молод. учених, Харків, 11–12 трав. 2022 р. / Харків. нац. пед. ун-т ім. Г. С. Сковороди. Харків, 2022. С. 219–221. URL: https://dspace.hnpu.edu.ua/server/api/core/bitstreams/76557bd3-7461-4dd0-913b-c367c8d75b26/content.
26.          Чуманська С. Використання інноваційних технологій на уроках математики як умова соціалізації учнів. Таврійський вісник освіти. 2015. № 1 (149). С. 178–183. URL: http://www.irbis-nbuv.gov.ua/cgi-bin/irbis_nbuv/cgiirbis_64.exe?C21COM=2&I21DBN=UJRN&P21DBN=UJRN&IMAGE_FILE_DOWNLOAD=1&Image_file_name=PDF/Tvo_2015_1_31.pdf.
27.          Янголь Н. Психолого-дидактичні аспекти впровадження розвивального навчання математики в освітній процес. Матеріали ІІ Міжнародної науково-практичної інтернет-конференції «Проблеми та перспективи розвитку науки на початку третього тисячоліття у країнах Європи та Азії» // Збірник наукових праць. Переяслав-Хмельницький, 2014. С. 98–100. URL: http://conferences.neasmo.org.ua/uploads/conference/file/5/conference_30-31.5.2014.pdf#page=98.

[1]Буйницька О. Цікавість як засіб підвищення ефективності навчання фізики. Фізика і астрономія в школі. 2007. № 1. С. 24–35.

[2]Лимар Ю., Чекан Ю. Нові професійні ролі вчителя в умовах Нової української школи. Інноваційна педагогіка. 2019. Вип. 15. Т. 2. С. 100–103. URL: https://dspace.chnpu.edu.ua/jspui/handle/123456789/780.

[3]Андрущенко В. Формування особистості вчителя в сучасних умовах. Політичний менеджмент. 2005. № 1. С. 58–69. URL: http://www.irbis-nbuv.gov.ua/cgi-bin/irbis_nbuv/cgiirbis_64.exe?C21COM=2&I21DBN=UJRN&P21DBN=UJRN&IMAGE_FILE_DOWNLOAD=1&Image_file_name=PDF/PoMe_2005_1_9.pdf.

[4]Пасічник О. Вікові особливості учнів 5-6-х класів та їх вплив на добір змісту навчання іноземних мов. Проблеми сучасного підручника. 2020. Вип. 25. С. 88–102. URL: https://ipvid.org.ua/index.php/psp/article/view/57/56.

[5]Жидецька О., Григор’єва Т. Урахування вікових особливостей учнів старшої школи під час викладання іноземної мови. Теорія і методика навчання і виховання. 2020. С. 16–18. URL: http://eprints.zu.edu.ua/31296/1/%D0%96%D0%B8%D0%B4%D0%B5%D1%86%D1%8C%D0%BA%D0%B0%20%D0%9E.%D0%9E._%D0%A2%D0%B5%D0%B7%D0%B8%202%28%D1%80%D0%BE%D0%B7%D0%B4%D1%96%D0%BB%201.3%29.pdf.

[6]Докучина Т. Мотивація навчання як запорука стимулювання учнів до досягнення успіху. Педагогічна освіта: теорія і практика. 2011. Вип. 8. С. 32–37. URL: http://www.irbis-nbuv.gov.ua/cgi-bin/irbis_nbuv/cgiirbis_64.exe?C21COM=2&I21DBN=UJRN&P21DBN=UJRN&IMAGE_FILE_DOWNLOAD=1&Image_file_name=PDF/znppo_2011_8_7.pdf

[7]Дзюбко Л., Гриценок Л. Мотивація навчальної діяльності як психолого-педагогічна проблема. Психолінгвістика. 2009. Вип. 4. С. 33–43. URL: http://www.irbis-nbuv.gov.ua/cgi-bin/irbis_nbuv/cgiirbis_64.exe?C21COM=2&I21DBN=UJRN&P21DBN=UJRN&IMAGE_FILE_DOWNLOAD=1&Image_file_name=PDF/psling_2009_4_5.pdf.

[8]Сірант Н., Кисіль Н. Інноваційні технології навчання на уроках математики в початковій школі. URL: https://pedcollege.lnu.edu.ua/wp-content/uploads/2015/09/%D0%86%D0%9D%D0%9D%D0%9E%D0%92%D0%90%D0%A6%D0%86%D0%99%D0%9D%D0%86-%D0%A2%D0%95%D0%A5%D0%9D%D0%9E%D0%9B%D0%9E%D0%93%D0%86%D0%87-%D0%9D%D0%90%D0%92%D0%A7%D0%90%D0%9D%D0%9D%D0%AF-%D0%9D%D0%90-%D0%A3%D0%A0%D0%9E%D0%9A%D0%90%D0%A5-%D0%9C%D0%90%D0%A2%D0%95%D0%9C%D0%90%D0%A2%D0%98%D0%9A%D0%98-%D0%92-%D0%9F%D0%9E%D0%A7%D0%90%D0%A2%D0%9A%D0%9E%D0%92%D0%86%D0%99-%D0%A8%D0%9A%D0%9E%D0%9B%D0%86.pdf.

[9]Білик Т. Інтеграція інноваційних елементів та інтерактивних технологій на уроках математики в початковій школі. Сучасні інформаційні технології та інноваційні методики навчання в підготовці фахівців: методологія, теорія, досвід, проблеми. 2021. Вип. 61. С. 100–108. URL: https://vspu.net/sit/index.php/sit/article/view/3026.

[10]Голодюк Л. Формування навчально-дослідницьких умінь учнів на уроках математики. Наукові записки. 2015. Вип. 7. С. 32–38. URL: http://www.irbis-nbuv.gov.ua/cgi-bin/irbis_nbuv/cgiirbis_64.exe?C21COM=2&I21DBN=UJRN&P21DBN=UJRN&IMAGE_FILE_DOWNLOAD=1&Image_file_name=PDF/nz_pmfm_2015_7(3)__8.pdf.

[11]Дичківська І.М. Інноваційні педагогічні технології: Навчальний посібник. К.: Академ.видав., 2004. 352 с.

[12]Барабаш І. Використання інноваційних технологій на уроках математики. Сучасний рух науки: тези доп. XI міжнародної науково-практичної інтернет-конференції, 8-9 жовтня 2020 р. Дніпро, 2020. Т.1. С. 42–43. URL: http://dspace.puet.edu.ua/bitstream/123456789/10005/1/11th%20Conference%20Part%201.pdf#page=42.

[13]Толок Д., Дейніченко Т. Інноваційні форми і методи в навчанні математики. Інноваційні педагогічні технології в цифровій школі : тез доп. учасників IV Всеукр. (з міжнар. участю) наук.-практ. конф. молод. учених, Харків, 11–12 трав. 2022 р. / Харків. нац. пед. ун-т ім. Г. С. Сковороди. Харків, 2022. С. 219–221. URL: https://dspace.hnpu.edu.ua/server/api/core/bitstreams/76557bd3-7461-4dd0-913b-c367c8d75b26/content.

[14]Полякова О. Інноваційна освітня діяльність вчителя початкових класів на уроках математики. Інноваційна діяльність педагога в умовах реформування шкільної освіти. 2015. С. 23. URL: https://elibrary.kubg.edu.ua/id/eprint/12303/1/O_Polyakova_IDPvURSCHO_IPPO.pdf.

[15]Чуманська С. Використання інноваційних технологій на уроках математики як умова соціалізації учнів. Таврійський вісник освіти. 2015. № 1 (149). С. 178–183. URL: http://www.irbis-nbuv.gov.ua/cgi-bin/irbis_nbuv/cgiirbis_64.exe?C21COM=2&I21DBN=UJRN&P21DBN=UJRN&IMAGE_FILE_DOWNLOAD=1&Image_file_name=PDF/Tvo_2015_1_31.pdf.

[16]Ткач К., Гоменюк Г. Інтерактивні методи навчання на уроках математики з використанням ІКТ. Сучасні цифрові технології та інноваційні методики навчання: досвід, тенденції, перспективи. 2022. № 9. С. 184–187. URL: http://dspace.tnpu.edu.ua/bitstream/123456789/27599/3/Tkach_Gomenuk.pdf.

[17]Ковтонюк Г. Роль позакласних заходів в організації самостійної пізнавальної діяльності школярів з математики та фізики. Нова педагогічна думка. 2016. № 2 (86). С. 66–68. URL: https://library.vspu.net/jspui/bitstream/123456789/3397/1/%D0%9A%D0%9E%D0%92%D0%A2%D0%9E%D0%9D%D0%AE%D0%9A%20%D0%93%D0%9C_2016_%D0%BD%D0%BE%D0%B2%D0%B0%20%D0%BF%D0%B5%D0%B4%20%D0%B4%D1%83%D0%BC%D0%BA%D0%B0_%D1%80%D1%96%D0%B2%D0%BD%D0%B5.pdf.

[18]Годованюк Т. Позакласна робота з математики. Методика, освіта, пошук. 2011. С. 19–24. URL: https://dspace.udpu.edu.ua/bitstream/6789/547/1/%D0%93%D0%9E%D0%94%D0%9E%D0%92%D0%90%D0%9D%D0%AE%D0%9A_6.pdf.

[19]Войненко К. Позакласна робота з математики як засіб розвитку математичних здібностей молодших школярів. Сучасні технології формування логіко-математичної компетентності в дітей дошкільного та молодшого шкільного віку / за заг. ред. Н. П. Тарнавської., Н. Ю. Рудницької, Ю. М. Мурашевич Житомир: ФОП «Левковець», 2015. С. 87. URL: http://eprints.zu.edu.ua/23991/1/14.PDF.

[20]Орел Л. Позакласна робота з математики як засіб розвитку математичних здібностей молодших школярів. Вісник Житомирського державного університету ім. І. Франка. 2005. Вип. 24. С. 254–257. URL: http://eprints.zu.edu.ua/3776/1/05olomsh.pdf.

[21]Жигайло О. Використання інноваційних технологій у позакласній роботі з математики вчителями початкових класів. Збірник наукових праць Херсонського державного університету. 2016. Вип. 74 (1). С. 114–119. URL: http://www.irbis-nbuv.gov.ua/cgi-bin/irbis_nbuv/cgiirbis_64.exe?C21COM=2&I21DBN=UJRN&P21DBN=UJRN&IMAGE_FILE_DOWNLOAD=1&Image_file_name=PDF/znppn_2016_74(1)__25.pdf.

[22]Кукуєва А. Позакласна робота з математики в старшій школі. Наукові записки молодих учених. 2019. № 3. С. 75. URL: https://phm.cuspu.edu.ua/ojs/index.php/SNYS/article/view/1602/pdf.

[23]Коршун Ю. Роль алгебраїчного апарату у розвиваючих іграх. Магістерські студії. Альманах / ред. кол. : Д. С. Мальчикова, Т. С. Корнішева. Херсон ; Івано-Франківськ : ХДУ, 2023. Вип. 23. С. 510–514. URL: http://ekhsuir.kspu.edu/handle/123456789/18710.

[24]Назаренко І. Елементи розвиваючого навчання на уроках математики у 5-6 класах. Збірник наукових праць викладачів, аспірантів, магістрантів і студентів фізико-математичного факультету (до 100-річчя від дня народження Миколи Федоровича Гур’єва). Полтава: АСМІ, 2010. С. 104–105. URL: http://dspace.pnpu.edu.ua/bitstream/123456789/3965/1/fakultet2010.pdf#page=104.

[25]Семенець С. Аспекти реалізації розвиваючої функції навчання при вивченні математики. Національна освіта: традиції та новації у контексті ідей І. Огієнка. 2002. С. 178–180. URL: http://eprints.zu.edu.ua/19895/1/Semenets_Aspekty_realizatsii_rozvyvayuchoji_funktsiji.pdf.

[26]Янголь Н. Психолого-дидактичні аспекти впровадження розвивального навчання математики в освітній процес. Матеріали ІІ Міжнародної науково-практичної інтернет-конференції «Проблеми та перспективи розвитку науки на початку третього тисячоліття у країнах Європи та Азії» // Збірник наукових праць. Переяслав-Хмельницький, 2014. С. 98–100. URL: http://conferences.neasmo.org.ua/uploads/conference/file/5/conference_30-31.5.2014.pdf#page=98.

[27]Жерновникова О. Особливості сучасного уроку математики. Педагогіка і психологія. 2013. Вип. 43. С. 27–33. URL: http://www.irbis-nbuv.gov.ua/cgi-bin/irbis_nbuv/cgiirbis_64.exe?C21COM=2&I21DBN=UJRN&P21DBN=UJRN&IMAGE_FILE_DOWNLOAD=1&Image_file_name=PDF/znpkhnpu_ped_2013_43_7.pdf.