змјст

ВступЗ

I. Методи розв'язування задач на екстремуми4

    П.              на екстремум в

    III.                на екстремум в стереометрй .25

Висновок .31

32

Вступ

Багато задач геометричного 3MiCTY € типовими задачами на екстремум, У

цих задачах при  певних умов треба знайти  або найменше значення певноТ геометричноТ величини (периметра, об'€му). з цих величин можна поставити у  певну формулу не одну), жа виража€ шукану величину, як  величина Проте сама в готовому не даегься. ћ' треба визначити з умов Часто за умовами можна побудувати  не 3MiHH0i, а двох.

застосувавши теореми, одну з цих                виключають.

€ чимало елементарних, досить простих i наочних, штучних, розв'язання на екстремум, враховують  Проте апарат  числення дае загальний розв'язання

на екстремум. Розв'язуючи     цим методом, будемо додержуватись такт

1)   незалежнот 3MiHH0i i визначення множини значень;

2)   побудова функцй, яка описуе ту геометричну величину, оптимальне

значення якот треба знайти в

3)    критичних точок  i розгляд тих,  належать

визначення функцй;

4)   з'ясування характеру екстремуму функцй• в цих точках;

5)   обчислення значень функцй' в цих точках i на що е областю визначення, i або найменшого з них. Якщо неперервна  i мае единий

екстремум, то у випадку максимуму — це буде  значення, а у

випадку MiHiMYMY — найменше,

Методи розв'язування задач на екстремуми.

Розглянемо  розв'язування задач на знаходження та MiHiMYMiB в на простих прикладах.

Метод оцгнки.

Задача. Точка М рухаеться по контуру квадрата ABCD. яким найменшим кутом може бути видно квадрата з точки М ?

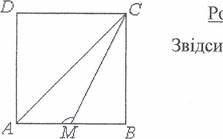Розв'язання. Очевидно, що 90 ⁰ ИМС 180⁰ . min ( ZAMC ) 90⁰ е

Зддщд, Визначити, якоТ  товщини дерево. можна  на BepcTaTi з круглою пилою, якщо ТТ  300 мм, BPi3 АВ дисковот пили в дерево 500 мм.

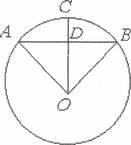Розв'язання. Позначимо через h товщину дерева, яка не повинна перевищувати CD, тобто h<C.D. CD виражаеться через ОС, ОВ i BD так: CD ОС — 0D

ОС — ОВ² —BD ² 134. мм, то

тах (h) 134,

Осьова симетрЈя.

Задача. Побудувати АВ (A(l;4) i В(5;-2)). Знайти симетричний АВ oci Ох.

Розв'язання. Використовуючи координати точок А i В, можна побудувати

спочатку               АВ, а          — AlBI , симетричний               АВ oci Ох.

AlBl матимуть координати А довжини  АВ i АЕ+ЕВ, АВ i АК+КВ, АВ i АЕ+Щ, i А]Е+ЕВ, можна зробити висновок, що ЕВ=ЕВь AE=AlE,

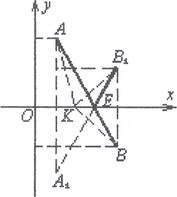
Таким чином, AB=AlBrAE+EBl -АЕ+ЕВ< АК+КВ.

Отже, сума АЕ+ЕВ буде не будьякот довжини ламаноТ АК+КВ, де Кг лежить на oci Ох, В — симетрична          Д  oci Ох. цього висновку можна приступити до розв'язування    на екстремуми з

використанням осьовоТ симетрй.

Паралельне перенесення.

Цей метод застосовують  при  задач на

знаходження найкоротшоТ даними i шуканими точками, яка

залежить

          Задача. Де треба побудувати MiCT через             з паралельними берегами,

щоб               пунктами А i В,  з                60kiB             була

найкоротшою? MiCT з берегом         утворюе куг а = 80⁰ .

Розв'язання. Насамперед корисно розглянути Taki

1.  Знайти найкоротшу двома пунктами А i В.

2.  З 60kiB  два  пункти. У якому MiCTi треба побудувати MiCT через ширина якот дуже мала?

Уявимо, що один i3  разом з одним населеним пунктом ”перенесли” паралельно нкий становить з берегом кут 80 ⁰, до другого берега так, що крат злились в одну пряму. Точка А переноситься вздовж моста на його довжину в точку А]. Якщо вважати, що  ”зникла”, то задача буде  до попередньоТ. Залишилось сполучити точку А] з точкою В. Точку перетину AlB з берегом позначимо буквою Е. цього пропонуемо берег ”перенести” в

початкове положення. При цьому точка А] повернеться в точку А, точка Е — в точку М, яка i визначить положення моста ЕМ, а AlE займе положення АМ. Ламана АМЕВ буде найкоротшим шляхом з точки А в точку В через MiCT МЕ. При будь-якому  моста шлях з точки А в точку В буде довшим. Нехай MiCT проходить через точки Xi У. шлях з точки А в точку В буде визначатися ламаною АХУВ. Щоб довжину IXi€i ламанот з довжиною ламаноТ АМЕВ, “перенесемо” один з  так, щоб крат злились в одну пряму. При цьому точка Х перейде в точку У, точка А — в точку А],  АХ — у  АЈУ. Довжина шляху з точки А в точку В

ламанот А1 УВ i  моста. Довжина ламаноТ А) УВ довжини ВАЈ i шлях з точки А в точку В через MiCT ХУ буде довшим, через MiCT МЕ.

Поворот площини навколо точки.

У задачах цього циклу поворот площини навколо точки мае той самий характер, що i паралельне перенесення; переводить частини у положення, зручне для розгляду i розв'язування

Зддцдщ гострого кута ЕАК задано точку М Побудувати на його сторонах Taki точки В i С, що АВ=АС i сума МВ+МС найменша Точка В належить АЈС, точка С -- АЕ.

Розв'язання. Використовуемо метод перетворення площини.

елементом у  € сума МВ+МС, тобто х МВ+МС Числове значення елемента х залежить двох точок В i С. Розв'язування зведемо до визначення одкйет точкие З метою застосуемо поворот площини навколо точки А на И = а , Точка В перейде в точку С, точка С у точку С , а точка М— у точку М? . Тепер легко  що числове значення х = мс: +ВМ=МС+СМ' залежить  точки С, яка визнача€ граничне значешш елемента х =МС+СМ', тому = мс; +ClM', де М' — образ точки М при

n0BopoTi навколо точки А на кут а . Шуканими точками € Т i С], де С] — точка перетину ММ' з АЕ.

Метод перебору.

            Розглянемо задачу, в                   знаходження  (найменшого)

значення залежить взаемного

Задача. Лист p03MipoM 400х500 мм  згорнути в трубку так, щоб поверхню, яка обмежуе  06' ем.

           Розв'язання. Лист                p03MipoM 400х 500 мм можна згорнути двома

способами. У першому випадку V =                 =ИН-РН 400² .500

     20000000           ²

(мм), де l=400 мм i +500 мм. У другому випадку V=nr ²ffl -

                      500² .400 25000000          

(мм ), де lr500 мм i Њ=400 мм.

два випадки, можна зробити висновок, що об'€м мае  висота якого 400 мм.

на знаходження i найменших значень зручно розв'язувати за таким планом:

1.   Визначають  величину (тобто величину,  чи

найменше значення якот треба знайти) i позначають ТТ, наприклад, буквою у

(або S, Р, r, R i т.д. в умови

2.   Одну з  величин (сторону, кут i т.д.) беруть як незалежну 3MiHY i позначають ТТ буквою х; встановлюють (у  з

умовою х.

          З, Виходячи з конкретних умов данот              виражають величину у через

х i     тобто          за умовою   величини (етап геометричного розв'язання

4.    Для одержання на попередньому  f(x) знаходять або найменше значення (в  з умовою по промЬкку реальноТ х, знайденому в п. 2.

5.    ]нтерпретують результат п. 4 для даноТ конкретноТ геометричнот

На перших трьох етапах складаеться, як прийнято говорити, математична, тобто  модель дано:        Туг часто    розв'язання залежить розумного вибору незалежнот 3MiHH0i, Важливо, щоб було  неважко виразити у через х. На четвертому    складена математична модель методами математичного елементарними способами. В момент такого  сама геометрична задача, якот для створення математичнот не  I лише коли завершиться розв'язок        в рамках складеноТ математичнот       отриманий результат  для вихтнот геометричноТ     (п'ятий етап).

Згадаемо план розв'язку методами  числення на знаходження  або найменшого значення функцй' у f(x),

Х:

1)знаходять f '( х ) ,

2)знаходять  i kpwnwHi точки для функцй' f(x), тобто точки, в яких f х )     0 або f х ) не iCHye, вибирають з них Ti точки, належать Х;

З) складають таблищо значень функцй у = f(x); в цю таблицю вносять значення функцй в точках, знайдених в п. 2), а також на  Х.

Якщо Х не мае своТх то в таблицю вносяться f(x) на його kiHIYIx.

Розглянемо два   до розв'язку стереометричних задач на знаходження  та MiHiMYMiB  геометричний та aHaJIiTWHVii  методи в  час все      i методами        використання яких ми вище розглянули.

Вважають, що  математичний дозволив за допомогою числення стандартно розв'язувати на знаходження ekcTpeMYMiB, то немае  у  геометричних i Але  пам'ятати, що бувають випадки, коли задача легше розв'язу€ться суто геометричним способом, не математичний       використовуе pi3Hi прийоми для знаходження ekcTpeMYMiB. Можна привести багато  методи приводять швидше до результату,          методи числення.

II. Задачй на екстремум в 11.yuaHiMeTpfl'.

Розглянемо ряд геометричних задач, розв'язання яких зводиться до екстремуму певшж

Задача. З ycix прямокутних  i3 заданою  с знайти той, у якого площа.

Розв'язання. Якщо х i у — катети трикутника, то у= с² -х ² , i площа трикутника

                                         1

S(x)

2 площа — HeBi)l'€MHa величина, тому областю визначення функцй

S(x) е [0; с].  S(x) набувае  значення одночасно з функцто f(x)=c х -х .

f ^f(x) =2х(с²-2х²)

то, розв'язавши

 — 2х ² ) = 0

знайдемо точки

          3MiCTY лише одна з цих точок:             З виразу похтноТ

видно, що f (х)>0 при х <f                       при х <           А це означае, що С

2

точкою максимуму а отже, i                             S(x), причомуkpiM

с

того, S(o)=S(c)=0, тому S(x) унабувае значення. Але при

       с                                             С

х           також i другий катет у             а це означае, що трикугник

Отже, з ycix прямокутних i3 заданою мае площу.

          Здудцеццд,. Розв'язок I!i€i                      досить легко знайти геометричним

способом.  вершини прямокутних  довжини лежать на  якого е ця  площу матиме

прямокутний трикутник, у якого  висота, Такою висотою е перпендикуляр до середини  довжина якого

Зддцущ, З ycix прямокутних  i3 заданою висотою h знайти той, що мае найменшу площу.

Розв'язання.

	Нехай	л АВС              прямокутний,
в	zACB	CD=h.

sin х cos х
(за умовою  i х             тобто sin	i cos # 0), то для визначення

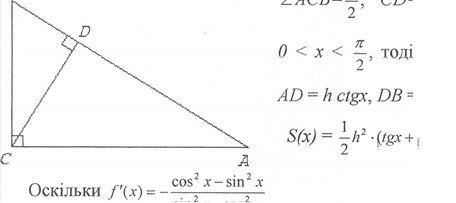Позначимо CAD=x,

                                                                                       ZDBC            ха

2

= h iAB = АТ) + DB, то

2 критичних точок функцй sinx cos х, sin х - cos х маемо:

к 20

                   4                         4

В iHTel)Ba.Hi (0, —) ЛФКИТЬ ЛИШе ОДНа ТОЧка:         як1й в:дпов1да€ L)BC— 4         4

а це означа€, що А АВС —  причому  f'(x) <(),

якщо х е (0, ^Щ), f'(x)              якщо х е (— —), то х           едина точка MiHiMYMY

4

            i S(x). Тому в           х         функцйУ(х) i S(x) набувають найменшого

4 значення. Отже, з ycix прямокутних  i3 заданою висотою мае найменшу площу.

Зауваження. У щойно наведеному  за належну 3MiHHY взято величину одного з прилеглих до  kYTiB. Можна дати

розв'язання, взявши за належну 3MiHHY довжину проекцй• одного з kaTeTiB на Нехай, наприклад, AD — х, DB АВ — х.

 — х(АВ—х), то АВ = х + площа трикутника як х набере

х вигляду:

2

S(x) —

2х

2        х то критичними точками функцй S(x) е: х] =/7, х2 -h Умову     задовольняе одна точка: А. Але при x—h трикутника АВС мае довжину 2h, а це i означае, що трикутник  Легко переконатись, що його площа € найменшою.

Зада.дщ З ycix  i3 заданою площею S i заданою основою с

знайти той, що мае найменший периметр.

Розв ' язання.

Нехай у д АВС: АВ с i CD — його висота,

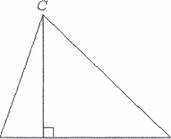
 S = —с ,CD.  площа i основа

трикутника одночасно визначають висоту трикутника, то позначатимемо CD h.

Якщо позначати AD х, 0 < х < С, то DB — с - х,

А         D                                в

свi периметр

трикутника як функц{я х небере вигляду:

                 Р(х) = с                        + У ² + (с — х)² -4- 17 ²

то розв 'язання 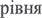х • +ћ ² —(с—х) х ² +17 ² = О

С

знайдемо критичну точку функцй• Р(х):           а значить д АВС

                                                                                   2                                2

 його периметр Р(—) = с+ с ² +4/7 ² . Легко переконатися, що

х едина точка MiHiMYMY на (0; С), 60 Ё(х) <0, якщо х е (О; ^Д) i Д(х) > 0, 2

якщо

х е (^Е ; 0). Тому в  х                 с  Р(х) набувае найменшого значення.

2

Отже, з ycix  i3 заданими площею i основою  мае найменший периметр.

Задача. З ycix  i3 заданими основою с i кутом 7 при знайти той, що мае

Розв ' язання.

Нехай у д АВС: АВ с, а zACB — у. Якщо

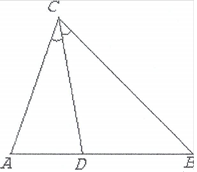                                                  CD —  то zACD              zDCB

2

Позначимо zGBD х, 0 < х < т-7 zCDB - T-(x+ ^L) i zCAB т-(х+7). З дСВГЭ

                                                 за теоремою                       для  CD

отримаемо:

sin(T — (х + —) sin(x + _ )

CB.sinx

sin(x + —)

З ДАСВ за Ti€k) самою теоремою для СВ знаходимо:

              св          АВ

          sin(T — (х + у))    sin у

останне значення СВ у праву частину виразу для  Ас, отрима€мо:

с • sin xsin(x + 7) sin у sin(x + — )

Легко переконатись, що

р с(х) — 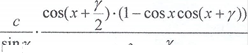sin2(x + — )

Розв ' язавши

cos(x + —)(1 — cos х cos(x + 7)) = 0,

знаходимо точки функцй ре (х):

                       к 20.

розв'язку не мае.  при к=() х €  тому

х               Але             також i Е САВ                             а це означае, що А АВС

                                      2 2 '  

 Якщо х е (0; —-—), то р                  i  рс(х) зростае, а якщо

х е (                  т—7), то р i (х)<0 i  рс(х) спадае. А це означае, що х

2 2 '

€ единою точкою максимуму на (0; л-7), в        рс(х) набува€ значення: Д (         —ctg— . Отже, з ycix    i3 заданою

2

основою i протилежним кутом

Задача З ycix  i3 заданими основою с i периметром 2р знайти той, у якого опущена на основу висота € найвищою.

Розв'язання Якщо а, Ь, с — довжини CTOPiH трикутника, а 2р -- його

периметр, ТО hc ²

        Нехай АВ = с,           АС+СВ+АВ = 2р, CD=hc . Позначимо АС          х,

СВ 2р — с — х.  значення 3aMicTb а i Ь у формулу для hc, отримаемо

2

                                                                      р(р — с)(р —                              — р + х) .

            hc(x) 20,             коли р

 hc(x) досягае  значення коли його досягае  А це квадратична  яку можна подати у такому

f(x) = —х ² + (2 р— с)х— р ² + ср

х=р-— € единою точкою максимуму функцй f(x) i hc(x). Тому

набувае  значення:                                       . Але

2

при  а це означае, що д АВС —  Отже, з

ycix  i3 даними основою i периметром  мае висоту.

Задача. З ycix  i3 заданими основою с i периметром 2р знайти той, у якого проведена до основи € найменшою.

Розв'язання. Довжина тс трикутника визначаегься через довжини його CTOPiH а, Ь, с за такою формулою:

1

2(а + Ь) ² — 4ab —с ² 2

Нехай у А АВС АС+СВ+ АВ = 2р,; АВ=с i AD=DB. Введемо позначення: АС=х, 0<х<2р-с. СВ=2р-с-х.  значення 3aMicTb а, Ь, с у

формулу для тс, отримаемо:

1

2(2р — —4х(2р — с— х) — с ²

2

2 р— с— 2х

то розв'язавши

2р-с-2х 0,

знаходимо критичну точку тс(х): х = р-

2

Легко переконатися, що  якщо х е (О;р-—), i т?  якщо

с

2 ' 2р-с), тому Р-2 € точкою MiHiMYMY  тс(х), причому

тс(р-з)- Р(Р-С) ,  р-                    едина точка MiHiMYMY на (0;2р—с), то

2        с

              тс(х) у                                      набува€ найменшого значения. Але при

2

х АС — р-— також i СВ — р          а це означае, що ЛАВС — 2 '

Отже, з ycix TpkYTIMkiB i3 заданцми основою i периметром мае найменшу

Задщщ, З ycix  три сторони яких мають однакову

довжину а, знайти ту, яка мае площу.

Розв ' язання.

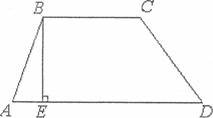нехай АВ ВС СИ)

ТОт ВЕ а sin х, АЕ

а, zBAD = х,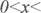

2 а cos х, а площа

S(x)—a sin х (l+cos х),

S(x) — a²(2cos х + cos х — 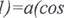х +1)(2 cos х 1),

S(x): хк tarccos— +2Кт, КМ).

                —) лежить                  одна з них: arccos—           причому

2

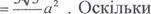 S ^f (Х)>0, ЯКЩО Х Е (0; ), i S'(x) <0, якщох е (

4

то в  S(x) набувае  значення. Отже, з ycix

З

з трьома сторонами однаковот довжини

площу мае та, в якоТ кут при ocH0Bi

Задача. З квадратного листа i3 стороною а треба виготовити зверху коробку,  по кутах квадратики i загнувши YTBopeHi крат, Якою повинна бути сторона основи коробки, щоб об'€м був максимальним?

Розв' язання.

Позначимо через х довжину сторони коробки.

ДОВЖИНИ CTOPiH

 —(а—х), а об'€м коробки

= —(а — Х)Х2

а

                                                     3i 3MicT0M                     число х задовольняе

HepiBHicTb 0 < х < а, тобто належить

(0, а). Отже, задача не звелась до знаходження

1

E.rnvx61' тт.- тттого ттмптметмтма Жлп.јтстт17

2

Знаходимо

З

         V (х) = ах——х2          ах —х —0,

                               2                     2

2

тобтох 0 або х

2 З

27

А через те, що V(o)0 i V(a)=0, то  значення

                                                         2

И набува€, коли х —а , тобто

з

тах V(x) = V(—a)

значення  досягае [0; а], отже, i

(0; а). Таким чином, сторона основи коробки повинна

бути —а .

Задача, Площа  сфери piBHa 27 т . Яка висота

06' ему, вписаного в що сферу?

Розв'язання.

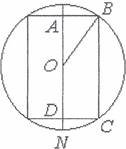
                                              Нехай                 утворений        обертанням

прямокутника ABCD навколо  MN. Побуду€мо

осьовий        площиною ABCD. Нехай м

AD = х, виразимо об'€м  х.

Одержали Sсфери ¯- 4лов ² , тобто 4тов² = 27т,

                                                            27                                                             ² ОВ² ОА ², тобто

                                      ов2          З дАОВ отрима€мо АВ —

4

2 27 х ² 27-х ²

                                       АВз формулою                      де

R — . Н — його висота, запишемо об'€м

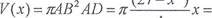(27-х ² ) т

—(27х-х3).

                                                                     4              4

За умовою  0 < х < 20В, тобто 0 < 36. Отрима€мо:

V (х) = 0, якщо 9  знаходимо х — З  х > 0). Якщо 0 < х < З, то V (х) >0, а якщо  то V   Значить, х  З        точка максимуму.

 и(х) визначена для будь-якого х i на мае одну критичну точку. Отже, при х — З и(х) досягае значення.

розглянемо  суто геометричних  розв'язування екстремальних задач. Один i3  Цей прийом дуже часто використовуеться при  найкоротших ламаних з вершинами на

заданих прямих i не

Задача. Довести, що серед BCix  вписаних в даний

гострокутний трикутник, найменший периметр мае трикутник з вершинами в ocH0Bi висот даного.

Розв' язання.

Bi3bMeM0 точку D на cTopoHi

гострокутного трикутника АВС. Знайдемо на АВ i

АС точки F i Е, так, щоб при заданому D периметр

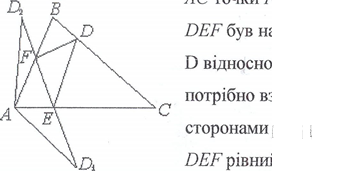DEF був найменшим. Нехай D] i D2 — точки симетрй

CTOPiH АС i АВ. В вершин Е i F noTpi6H0 взяти точки перетину DlD2 3i периметр трикутника

DEF DlD2, а периметр будь—

якого трикутника DElFl ламаноТ DlElFlD2 > DlD2.

Залишилось визначити положення точки D, при якому DlD2 е найменшим.

Розглянемо трикутник DlAD2. Кут при

2 z BAC), DIA L)2A DA. 3HaqHTb DID2 e HaiiMeH111HM, 11<1110 HaiMeH111MM e BiÅpi30K AD, T06TO AD — BHCOTa TPHKYTHHKa ABC. OCKiJ1bKM ÅOBeÅeH0 iCHYBaHH51 i

€ÅHiCTb MiHiMaJ1bHOEO (no nepvnueTpy) 'rpmcyTH11Ka AEF, TOAi, p03ÅYMH BiAHOCHO iH111ux CTOPiH TPHKYTHMKa ABC, npvriiÅeM0 110 BHCHOBKY, 1110 E i

F TaKO>K 110BHHHi 6YTH OCHOBaMV1 Binr10BiÅHnx BHCOT TPHKyrHHKa ABC

IHLIIHM KOPVICHVIMI npuii0M iJIK)cTpy€ HacTY11Ha 3amaqa.

3maqa. AaH0 Kyr Bej1H^LIHH010 a (a < 90⁰). O — Bep111HHa KYTa. Ha OAHiMf i3 CTOPiH Kyra B3flTa TO^LIKa A, OA a. T0YKa B p03MimeHa Ha Tiü xe cTopoHi, a M — Ha np0THJ10KHiii CTopoHi Tayc, Luo LAMB 90⁰ . 3HaiiTH HaiiMeH111e 3HaqeHH51

ÅOB)KH1-m BiApi3Ka AB.

P03B'S13aHHfl.

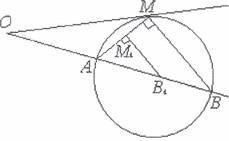Hexaü M i B 6YÅb=HKi ABi TO^IIKH Ha CTOPOHax KYTa, ÅJI% SIKHX LAMB 90⁰ (Man. l). orm111eM0 I-laBKOJTO TPHKYTHH1€a AMB KOJIO. SIKIIIO ue KOJIO nepeTHHa€ CTOPOHY KYTa, Ha 51KiM p03Mi1uy€Tbc51 TO^LIKa M, TO  Binpi3Ka AB MO)KHa 3MeH111UTH. CnpaBÅi, Hexaii Ml — 6YÅb-fl1€a TO^L11€a Ha XOPAi, ZAMIB > BiA110BiAH0, Ha AB iCHY€ TO^LIKa B], 51K0i LAMIBI 90⁰ . MH AOBeJIH, LAO AKLUO

MiHiMaJ1bHHii BiÅpi30K AB iCHY€, TO KOJIO, onncaHe 1--1aBKOJIO Tpvncy^rrmnca AMB, AOTHKa€TbC% cTOPOHV1 KYTa.

M0>KHa 3P06HTH it 110—iHIL10My: P03rJIAHYTH M i B TaKi, 1110 onucme KOJIO ÅOTHKa€TbCA CTOPOHH KYTa i AOBeCTU, 1110 BiÅpi30K AB, MH 0TpvnraJ1n, Mae HaiiMeH111Y AOB)KHHY. 3p03YMiJ10, 1110 B 110TPi6H0 B3srrn Ha Binpi3KY OA (MaJ1.2). TO^T-IKU Ml, BiÅMiHH0i Bin M, 6yne LAMB < 90⁰, a 3Ha^LIUTb BiAITOBiÅHa ^eroqrca Bl 3aiåMe 51Koro ABI >AB.

Знайдемо  АВ, який  цьому

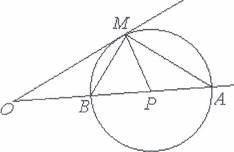
положенню точки М. Нехай Р — середина АВ,

АВ 2х, ОР — а — х. МР — х, дотична ОМш ОР (РМ

                                                                               zOMP = 90 ⁰, sina = х                       а sma

1 + sin а

Найменше значення довжини  АВ piBHe

2а sina

1 + sin а

Але не завжди вдаегься проробити роздуми, б доводили, що знайдене  peui3Y€ шуканий екстремум. Нагадаемо, що при

i найменших значень з допомогою математичного

ми опираемось на ствердження про або

найменшого значення. Дане твердження може бути' сформульоване в загальному  Але звернення до даного ствердження не 30BciM доведення загального факту в

сторони, в кожному конкретному випадку або найменшого значення достатньо очевидне.

погляди,     показують для яких  чи найменше значення не досягаеться,  теоремою  дають умови,   визначають екстремальне положення.

Задача,Довести, що проведена до  сторони трикутникаэ утворюе 3i сторонами, заключають, кути, величиною кожного з них не менше половини найменшого кута трикутника.

Розв ' язання.

Нехай в ААВС сторони се Ь 2 с, тобто АВ=с,

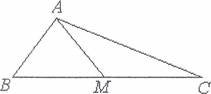
ВС=а, АС=Ь. Bi3bMeM0 на СВ точку М так, що и САМ =—ZC.

довести, що САК За теоремою для АСАМ запишемо:

АС sin

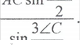
см

СЈЛ”/ =

zc 3ZC 3ZC sin sin(T — sm

Використаемо  формули для

zc:

перетворення виразу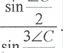

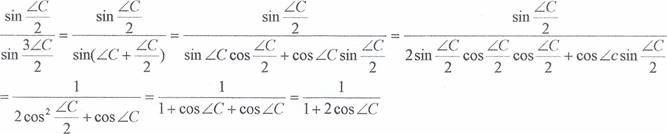
За теоремою для АВ з ААВС:

c² =a² +b²-2ab cos z С;

cosZC =

2ab

Використавши вище перетворення, запишемо:

zc

АС sin

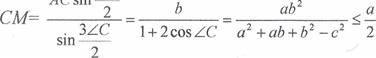
Задача. Трикутники АВС i АМС  так, що МС перетинае АВ в

О, причому АМ+МС АВ+ВС. Довести, що якщо АВ — ВС, то ОВ > ОМ.

Розв'язання,

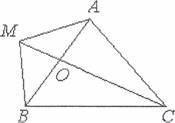Позначимо  АМ=с, МС=Ь, МВ=т, ЕВМО=ср, zMBO=y. довести, що ОВ>ОМ, або у, або costp<cosy.

Розглянемо трикутник МВА. Запишемо для

сторони АМ за допомогою теореми  piBHicTb:

с —т +а -2ат cosy,•

одержимо вираз для косинуса кута у :

соку =

2та

Розглянемо трикутник МВС. Використовуючи теорему запишемо для сторони ВС:

a^[1] =b² +m²-2mb coscp ;

Отрима€мо:

coscp =

2mb

m ² (b — а) — a(b ² с2)

Запишемо cos — cosrp =

                                            2та                                                2таЬ

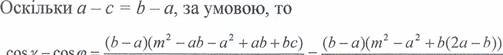
cosy — cos (Р

                                               2та                                    2та

(Ь — а)(т + Ь — а)(т — а + Ь)

2mab що й було довести.

Задача. Довести, що з ycix Tpm<YTWikiB 3i  кутом у при  i  CYMi довжини бокових CTOPiH а + Ь  трикутник мае найменшу основу.

Розв'язання Нехай а + b=q; а, Ь, с — сторони трикутника. За теоремою

запишемо:

с ² = а ² +b ² — 2ab соу = а ² +(q — —2a(q —a)cos7 =

 He3MiHHi, то найменше значення с буде при а = — =

2    2 тобто при а Ь.

Зддщщ З ycix  з однаковою основою i одним i тим же кутом при знайти трикутник з периметром

Розв ' язання.

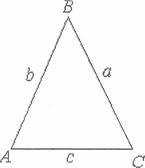
Розглянемо трикутник АВС з основою АС i позначимо через а, Ь, с --- довжини CTOPiH. Кути,        сторонам а, Ь, с

позначимо  Е А, zB, Z С. Покладемо

                                                      За теоремою             запишемо:

sinZA sin(ZA + ZB) sin ЕВ

Знайдемо периметр:

sinZA sin(ZA + ЕВ)

• sin(ZA + —) sin Х-В         sin ZB

sin

2

                   Ь > 0 i                      0, то р прийме  значення при

2

7—-44 +У даному випадку Е А = Е С i ААВС

             2       2

    III,              на екстремум в стереометрГЈ,

Задача. В конус i3 заданим об'€мом вписана в ocH0Bi лежить  трикутник, в якого кут при а. При якому  а об'ем буде

Розв ' язання.

з умовою, 06' ем конуса

 013 ² , де

                                                                 основи конуса, SO         висота.  з

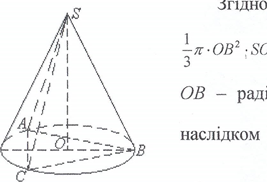з теореми -2.ов,

 АС = 2 .ОВ. sin ZABC = 2 • sina, де ОВ

кола, описаного навколо  (АВ—ВС) трикутника АВС, а

          i3          теоремою              в       трикутнику       АВС       маемо

АС ² - АВ ² + ВС: ² -2, • ВС: ИВС              або,        так                   АВ=ВС,        то

Ас: ² - 2ВС: ² -2 • ВС: ² .cosa = 2ВС ² (1- cosa),                                              вс:2

2(1 — cos а)

2

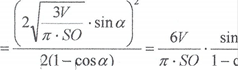sin ² а

1—cosa

1

         Площа               трикутника АВСSмвс,              АВ • ВС • sin ИВС =

2

  —ВС: 1       ² •sina = 1 6V sin ² a • sina = 3V                sin ³ а

=                                                                                                   

     2                       2 1T•SO 1—cosa                T•SO 1—cosa

Складемо тепер чјункцпо, значення яко; треоа знайти:

                                                              11 3V                              sin ³ а                       sin а

                               SABC ¯ мвс SO, або V(a) =                                     .so=

                                                                                    З z•SO 1—cosa               т 1—cosa

IlPOMbKOK 3MiHV1 apryMeHTY a B maH0MY BurraÅKY BH3Haqa€TbC% 3 YMOBU a e (O;n). TaK1dM HVfHOM, 3anaqa 3BeJ1aCb AO 3HaXO)VKeHHA Haii6iJ1b1110ro 3HaqeHH}1

(l)YHK11ii V (a) Ha np0Mimcy (0; 7t) . 3HaiineM0 KPMT1åMHi TOMKU uiei (l)YHK11ii:

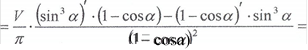
               Vf(a) = V sin a                 V sin a

                            I—cosa           n I—cosa

V 3sin ² a(sina) • (I—cosa)— sina•sin a V 3sin ² a (1 — cosa)²

(1 — cos 2 a) •(3cosa(1 —

cos 2 a))

V sin ² a •(3cosa(1 — cosa)— sin ² a) V

                            (1 — cosa)2                                        (1 — cosa)2

V (1 — cosa)• (1 + cosa)3cosa(1 — cosa) V (1 —cosa) (1 + cosa)

• — cosa) • (1 + cosa))

                               (1 — cosa)                             (1 — cosa)2

V (1 — cosa) ² • (1 + cosa) (3 cosa —1 cosa) V

• (1 + cosa) (2 cosa — 1).

(l — cosa)2

v ^t(a) = o, 511<1110 (1 + cosa) (2 cosa 1) = 0, 3BiÅKM a60 (l + cosa) = O,cosa = —l,a = It + 2m,

ne Z, a60 2 cosa —1 = 0, cosa =

3

CAHHOK) KPUTWIHOK) TOMKOK) (l)YHK11ii V(a) Ha np0Mi)KKY (O;n) € Tomca a = — . Ilpu

nepexoai qepe3 11K) 'ro^t1KY noxiÅHa  V (a) MiHf1€ 3HaK 3 rnuoca Ha MiHYC,

V(a)          —) i              Ha

V sin a

TaKHM HVIHOM             a =           (bymcui% V (a) =               Ha6YBa€ CBORO Hait6iJ1b1110ro

                                                3                                   7t I—cosa

3HaqeHH51 , T06TO             a =         06'€M nipaMinu € Hah6iJ1bL11ØM.

3

          .3aAaqa. 3HaiiTH Haii6iJ1b111Y            npoeK11ii KY6a Ha IIJIOIUUHY.

'

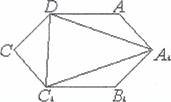B 3ara4bHOMY BHT1aAKY npoeK11i€K) KY6a e mecTHKYTHHK, rlPOTHJ10KHi CT0POHH mcoro 11011apH0 napaJ1eJ1bHi. Ha Ma.J110HKY 306p01€eHa npoercuifl KY6a i        iioro rpaHevi.

o^rrpmaaHoro meCTHKYTHUKa AA IBICICD B ABa

рази                                 трикутника AlClD. Але трикутник AlClD €

правильного трикутника 3i стороною ф

При  його площа може лише зменшитися. В максимальному випадку його площа не  Це мае якщо площина

паралельна  правильного трикутника, який ми розглядаемо. Таким

чином, максимальна площа проекцй куба piBHa 2

Зддщщ Дано куб ABCDAlBlClDl з ребром 1. Знайти найменшу

точки М,  на вписаному в ABCD, до точки М,  на вписаному навколо трикутника AlBD.

Розв'язання. Розглянемо           сфери з центром в	0 —    куба.
Перша дотика€ться до BCix ребер куба. Ii	—. Друга сфера

описана навколо куба. ћ•      Два даних кола належать цим сферам. 2

 М i N не може бути менше  цих сфер,

тобто менше  Залишилось довести, що ця                  досягаеться для

2

першого i другого кола. Для цього спроектуемо з точки 0 менше коло на сферу.

Отримаемо на коло, яке перетинаеться з колом, яке проходить через А 1, В i D.

Задача. В ocH0Bi чотирикутно; лежить прямокутник, одна сторона якого piBHa а, ребра  piBHi в. Знайти  значення об'ему

Розв'язання. Позначимо через х довжину двох CTOPiH прямокутника, який лежигь в ocH0Bi  обчислення об'ему скористаемось такою формулою Н, де — площа основи piBHa SOCH а. Знайдемо висоту

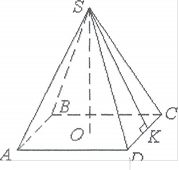
Запишемо АВ CD а; AD ВС х.

Розглянемо ADSC. Проведемо висоту Sk до сторони DC. Розглянемо ACICS, який е прямокутним.

теореми Sk SC² — СК?, тобто Sk²

Розглянемо AICOS, BiH прямокутний. За

теоремою запишемо: S0² — Sk² 0k², тобто S0² — (а²/4) — (х²/4).

Обчислимо 06' ем

а(4в ² — СР)

06' ем при х

12

Задача, Основою  € квадрат i3 основою а,

до основи, а  до основи кутом а. У вписують так, що чотири вершини

кожного з них лежать на              ребрах                а чотири — на ocH0Bi. Який i3

цих мае його.

Розв ' язання.

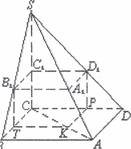                                               Якщо основа  SABCD              квадрат, то

перпендикулярними до нет можуть бути

                                                      Тх                      ребро SC також

перпендикулярне до площини основи.  CD AD ,

то       з теоремою про три перпендикуляри SD AD. в

Отже, ZSDC = а i висота гпрамти SC = C,Dtoa = atga ,

Верхню основу вписаного в дану можна

розглядати як площиною, паралельною ocH0Bi, тому основами

вписаних е квадрати.

Позначимо сторону основи i висоту вписаного буквами х i у. його об'ем V = х² у, де 0 < х < < у < atga. Визначимо у через

х. Якщо СР=х, то PD—a-x,  Отже, V = .х² (а - худа .

Знайдемо  значення J4ieT функцй• на (О;а), Очевидно, що коли х прямуе до 0 або а, то V пряму€ до 0. тому  значення набувае у  [О',а].

ј/ ? = (2ах— 3x2)tga г

V'                     коли 2ах=Зх , тобто при х=0, або х=—а. З  мђжувань

випливае, що й на (О;а) розглядувана  набувае  значення

4

при х= —а . При такому об'ем становитиме V = —a ³tga

27

Здцщд, В кулю вписана правильна п-кутна  При якому двогранному kYTi гранню i площиною основи  об'ем

буде

Розв'язання. Зображаемо на малонку п-у частину грань, МН — висота. Позначимо R, Нехай МВ = х.

     м                                      Виразимо V через х i R, Користуючись формулою:

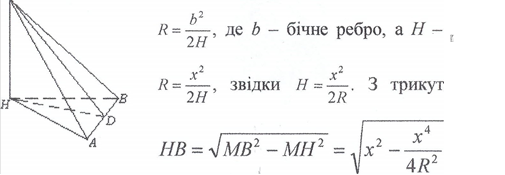
З трикутника МВН знаходим:

2 , Так якАВ сторона

правильного              п-кутника,            то             ИНВ =                   а            тому

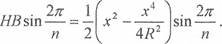
            = -АН • 2

Отже, V = —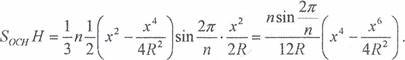

Знайдемо  значення  V = К х

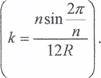
6х5

Маемо: =К 4х³ — Коли V ^f =0 - 4R2

 (0;2R) 4R2

= 0,Х2 —R

цих трьох значень (0; 2R) належить  При

               У (х) набувае                             значення. В знайти кут

MDH для  об'ему, де MD — висота Нехай

ЕМГЭН = (Р. Маемо: МН = З трикутника BDH                       знаходимо:

М) = HBcos                                                                                                  cos— тот tgrp =Отже, ТЭН

ф = arctg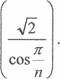

        Задача. Знайти                  основи  який при заданому 06'€Mi V мае

найменшу повну поверхню,

Розв'язання.

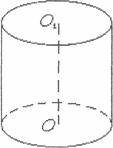
                                                       поЬ 2172 + 21TV — 2172 +            S(r)

 точка MiHiMYMY. Отже,

Висновок

 на екстремум в kypci re0MeTpii  не дуже часто. I при Тх виникають трудноп-ј. Тому imepec до них

Розв'язування таких задач сприяе розвитку  мислення, i

Мета

моет роботи — в типах i методах розв'язування таких задач. В p060Ti

поданий  теоретичний  i розглянуто класи задач,

об'€днаних  iL1e€k),  цих               показано

приклади розв'язування задач кожного класу i дана методика розв'язування складних задач.

Велика  взятих головним чином з вступних,

них, факультативних завдань з математики, демонстру€ pi3H0MaHiTHicTb що лежать в ocH0Bi цих задач, що е  маленькими математичними

загадками,

1.                      Бевз Г.П. Методика розв'язування стереометричних задач.  к..

Радянська школа, 1988. — 192 с.

2.                      Возняк ГЛЛ, Малашок К.П, Прикладна  курсу математики. — К.: Радянська школа, 1984. 79 с.

3.                      Голубев B.I.,  1.Ф. Факультативний курс з математики. — М., 1991. - 253 с.

4, Гусев ВЛ., Литвиненко В.Н„ Мордкович А.Г, Практикум по решению математических задач. — М.: Просвещение, 1985. — 223 с.

5.                                      задач з математики для  у ВУЗи. M.I.

CkaHaBi. — Москва, 1992. — 432 с.

6.                                      36ipmk науково—популярних статей, У CBiTi математики. — Китв, 1979.

з 12с.

7.                                      Карагодова 0,0. , Черняк 0.I.  задач з математики. — К.: Знання,

2000. -332 с.