Методика навчання математичної освітньої галузі (Дудар Ольги, ПО-31)
![]() Тема 5
Тема 5
Тема 5. Методика навчання арифметичних дій додавання і віднімання.
Табличні випадки додавання і віднімання
|
1 |
Підготовча робота до ознайомлення з діями додавання і віднімання |
|
2 |
Ознайомлення з арифметичними діями додавання і віднімання |
|
3 |
Переставний закон додавання |
|
4 |
Взаємозв’язок між діями додавання і віднімання |
|
5 |
Методика навчання табличного додавання і віднімання |
 Підготовча робота до ознайомлення з діями додавання і віднімання
Підготовча робота до ознайомлення з діями додавання і віднімання
|
Конкретний зміст арифметичних дій додавання і віднімання формується під час оперування учнями множинами предметів. |
|
|
Операція об’єднання двох множин, що не перетинаються, розкриває конкретний зміст дії додавання. |
Операція вилучення частини елементів множини розкриває конкретний зміст дії віднімання. |
|
Підготовча робота до введення арифметичної дії додавання за допомогою практичних вправ: |
Підготовча робота до введення арифметичної дії віднімання за допомогою практичних вправ: |
Об’єднати – означає присунути, змішати, зсипати тощо. |
Вилучити – означає відсунути, відрізати, відсипати, забрати тощо. |
|
|
|
|
Схематичне зображення операцій об’єднання або вилучення |
|
|
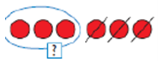
Об’єднуючи, обводять замкненою кривою лінією всі фігури.
|
Вилучаючи, закреслюють кілька фігур та обводять замкненою кривою лінією остачу.
|
|
Коли об’єднуємо, стає більше. Щоб стало більше, треба об’єднати. |
Коли вилучаємо, стає менше. Щоб стало менше, треба вилучити. |
![]()
Ознайомлення з арифметичними діями додавання і віднімання
|
2.1. Ознайомлення зі знаками «+» і «‒». Схематичний рисунок. Ознайомлення з термінами «знак рівності», «рівність», «вираз», «значення виразу» |
|
|
Об’єднати – означає додати. Додавання – це арифметична дія, яка виконується між числами. Таким чином, 5 і ще 2 – означає: до 5 додати 2, одержимо 7. В арифметичної дії додавання є свій знак «+» – плюс. Це можна записати так: 5 + 2 = 7. |
Вилучити – це означає відняти. Віднімання – це арифметична дія, яка виконується між числами. Таким чином, 8 без 3 – це значить від 8 відняти 3, одержимо 5. У арифметичної дії віднімання є свій знак «–» – мінус. Це можна записати так: 8 – 3 = 5. |
|
Коли об’єднуємо, стає більше. Об’єднати – означає додати. Тому коли додаємо, також стає більше. Отже, щоб стало більше, треба об’єднати – додати. |
Коли вилучаємо, стає менше. Вилучити – означає відняти. Тому коли віднімаємо, стає менше. Отже, щоб стало менше, треба вилучити частину – відняти. |
|
5 + 2 = 7 8 – 3 = 5 З’ясовують, що в цих записах спільною є наявність знаку рівності, тому їх можна назвати одним словом «рівності». Ліворуч від знаку рівності записані числа, що поєднані знаком «+» або «–»: 5 + 2 і 8 – 3 це вирази. Праворуч від знаку рівності записані числа 7 або 5 — це значення виразів. |
|
|
2.2. Перехід від схематичного рисунка до схематичного рисунка у вигляді відрізків |
|
|
Схематичний рисунок дії додавання:
|
Схематичний рисунок дії віднімання:
|
|
2.3. Додавання і віднімання числа 1 |
|
|
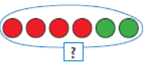
Як отримати наступне число? Щоб отримати наступне число, треба додати 1. Яке число отримаємо, якщо до 3 додамо 1? [Якщо до 3 додати 1, то отримаємо наступне число 4.] |
Як отримати попереднє число? Щоб отримати попереднє число, треба відняти 1. Яке число отримаємо, якщо від 5 віднімемо 1? [Якщо від 5 віднімемо 1, то отримаємо попереднє число 4.] |
|
2.4. Додавання та віднімання за числовим променем/ відрізком |
|
|
|
|
|
Коли додаємо, стає більше чи менше? Де на числовому промені розташовані більші числа? Праворуч. Отже, коли додаємо, за числовим променем, треба «крокувати» – рухатися праворуч – уперед. |
Коли віднімаємо, стає більше чи менше? Де на числовому промені розташовані менші числа? Ліворуч. Отже, коли віднімаємо, за числовим променем треба «крокувати» – рухатися ліворуч – назад. |
|
֍ Як додали число 2? [Додали 1 та ще 1; зробили 1 «крок» уперед та ще 1 «крок» праворуч – уперед. Щоб додати 2, зробили відразу великий «крок» уперед – праворуч, який містить 2 одиничні «кроки» праворуч – уперед.] Щоб додати число 2, праворуч «відкрокували» 2 одиничні відрізки. |
|
|
2.5. Назви компонентів і результатів арифметичних дій додавання і віднімання |
|
|
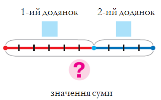
4 + 3 = 7 Числа, які додають, називають доданками. Таким чином, 4 та 3 – це доданки: 4 – це перший доданок, 3 – це другий доданок. Вираз, який записано ліворуч від знака «=», 4 + 3, називається так само, як і результат – сума! Значення виразу, число 7, також сума!
|
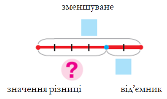
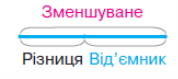
4 – 1 = 3 При відніманні число, від якого ми віднімаємо (4), зменшується, тому його називають зменшуваним. Число, яке віднімають (1), називають за характером дії від’ємником. І результат дії віднімання (3) називають так само, як і вираз, що записано ліворуч від знака рівності, але зі словом «значення» – значення різниці.
|
|
4 + 1 = 5 Рівність читаємо так: • сума чисел чотири і один дорівнює п’яти; • Чотири плюс один дорівнює п'яти. • Чотири і один дорівнюють п'яти. • Чотири додаються до одного, і виходить п'ять. • П'ять - це результат додавання чотирьох і одного. |
5 ‒ 1 = 4 Рівність читаємо так: • різниця чисел п’ять і один дорівнює чотирьом; • П'ять мінус один дорівнює чотирьом. • П'ять і один віднімаються, і виходить чотири. • Чотири - це результат віднімання п'яти і одного. |
|
2.6. Додавання та віднімання з числом 0 |
|
|
Якщо один із доданків число 0, то значення суми дорівнює іншому доданку. При додаванні нуля до будь-якого числа в результаті одержимо те саме число. |
При відніманні нуля від будь-якого числа в результаті одержимо те саме число. |
|
Додаючи й віднімаючи число 0, дістаємо те саме число. |
|
|
2.7. Віднімання однакових чисел |
|
|
|
Порівнявши число, від якого віднімають, та число, яке віднімають, встановлюють, що ці числа рівні, й роблять висновок: при відніманні рівних чисел в результаті одержимо число 0. |
 Переставний закон додавання
Переставний закон додавання
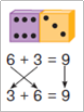 Ознайомлення з переставним законом додавання здійснюємо через порівняння рівностей, що складені за кісточками доміно, і підводимо дітей до формулювання закону на підставі індуктивних узагальнень.
Ознайомлення з переставним законом додавання здійснюємо через порівняння рівностей, що складені за кісточками доміно, і підводимо дітей до формулювання закону на підставі індуктивних узагальнень.
Прочитайте першу рівність. Прочитайте другу рівність. Що помітили? [Перший доданок став другим, а другий доданок став першим, значення суми від цього не змінилося.]
Аналогічне завдання можна запропонувати учням з арифметичними штангами, відрізками.
Від перестановки доданків сума не змінюється.
Від переставляння доданків сума не зміниться.
Буквений запис переставного закону додавання: ___________
Застосовуємо переставний закон додавання для знаходження значень виразів, для порівняння виразів, для знаходження суми трьох доданків.
Після розв’язання подібних завдань робимо висновок:
Зручніше до більшого числа додавати менше.
![]()
Взаємозв’язок між діями додавання і віднімання
 Взаємозв’язок дій додавання та віднімання розглядаємо як складання з однієї рівності на додавання двох рівностей на віднімання.
Взаємозв’язок дій додавання та віднімання розглядаємо як складання з однієї рівності на додавання двох рівностей на віднімання.
Об’єднуємо точки зліва направо: 6 + 3, усього точок 9,
6 + 3 = 9. Читаємо: перший доданок 6, другий доданок 3, значення суми 9.
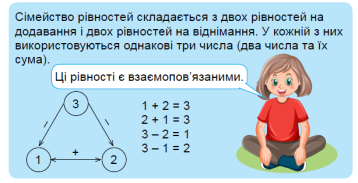 Якщо від суми двох чисел відняти перший доданок, то залишиться другий: 9 – 6 = 3.
Якщо від суми двох чисел відняти перший доданок, то залишиться другий: 9 – 6 = 3.
Якщо від суми двох чисел відняти другий доданок, то залишиться перший: 9 – 3 = 6.
Якщо від суми двох доданків відняти один доданок, то одержимо інший доданок.
|
Правило знаходження невідомого доданка (невідомої частини цілого) |
Правила знаходження невідомого зменшуваного і невідомого від’ємника |
|
Познайомити учнів із цими правилами можна через аналіз схематичного зображення компонентів та результату дій, через створення ситуації |
|
|
Наприклад, ситуація, коли відома сума і один доданок, а інший доданок невідомий: «В Івана у двох руках 7 паличок. У правій руці 3 палички, а скільки паличок у лівій руці, він нам не показав, і порахувати ми їх не можемо. Як дізнатися, скільки паличок в Івана у лівій руці?» Учні пояснюють за схематичним малюнком, що означають відомі числа та невідоме число, встановлюють, що відомі сума і другий доданок, отже, треба знайти перший доданок. |
Яке число найбільше при відніманні? За схемою поясніть, з чого складається зменшуване. [Із від’ємника і значення різниці.] Як одержати зменшуване? [Треба до значення різниці приєднати від’ємник.] Що означає приєднати? [Приєднати — означає додати.] Щоб знайти невідоме зменшуване, треба до значення різниці додати від’ємник. На схемі із зменшуваного вилучаємо значення різниці (прикриваємо її). Залишився від’ємник. Щоб знайти невідомий від’ємник, треба від зменшуваного відняти значення різниці. |
 Методика навчання табличного додавання і віднімання
Методика навчання табличного додавання і віднімання
Обчислювальні навички – це найвищий ступінь оволодіння обчислювальними прийомами.
Прийом обчислення – система операцій, яку потрібно виконати, щоб дія досягла своєї мети – це орієнтувальна основа дії (ООД). Таким чином, прийоми обчислення складаються з ряду послідовних операцій (системи операцій), виконання яких приводить до знаходження значення арифметичної дії над цими числами, причому вибір операції в кожному прийомі встановлюється тими теоретичними положеннями, які використовуються як його теоретична основа.
|
Методика формування обчислювальних навичок передбачає етапи: |
|
|
1) ознайомлення з прийомом обчислення, надання учням ООД (орієнтувальна основа дії); 2) виконання учнями нової дії, спираючись на матеріалізовані опори ‒ картки з друкованою основою, пам’ятки; 3) розгорнене виконання дії з промовлянням уголос кожного кроку пам’ятки (спочатку читаючи кожне завдання пам’ятки, а потім ‒ промовляючи своїми словами); 4) виконання дії з промовлянням «про себе» кроків пам’ятки, під час виконання дія скорочується ‒ виконуються лише основні операції; 5) виконання дії в розумовому плані, дія максимально скорочується та автоматизується. |
|
|
• На першому етапі засвоєння дії вимагаємо від учнів виконання розгорнених записів. • Після того, як учні засвоять послідовність операцій, що складають дію, і почнуть виконувати її з коментарем, форма дії змінюється ‒ вона засвоюється у формі голосного мовлення. На цьому етапі дія виконується також як повністю розгорнена, у записі фіксуються всі проміжні результати. • Якщо, коментуючи розв’язання, учні починають пропускати проміжні операції (вони у думці нібито звучать, але дитина не бажає витрачати час на її відтворення в голосному мовленні, у записі учень фіксує лише основні операції), це свідчить про те, що дія набула форми голосного мовлення про себе. • І нарешті, коли дія максимально скорочується й виконується нібито за формулою ‒ дія переходить у внутрішній план, дитина набуває обчислювальної навички. |
|
Порядок опрацювання випадків табличного додавання і віднімання |
||
|
1) додавання і віднімання числа 1 |
Що означає до будь-якого числа додати 1? [Додати 1 ‒ означає отримати наступне число.] Що означає від будь-якого числа відняти 1? [Відняти 1 ‒ означає отримати попереднє число.] Теоретична основа додавання та віднімання числа 1 – знання порядку розташування чисел у натуральному ряді. |
|
|
2) додавання і віднімання числа 2 3) додавання і віднімання числа 3 4) додавання і віднімання чисел 4, 5 5) узагальнення прийому додавання і віднімання частинами |
Теоретична основа додавання та віднімання чисел 2, 3, 4 і 5 – правило додавання суми до числа. Числа додають і віднімають частинами на підставі знання складу цих чисел.
|
|
|
2 ‒ це 1 і 1. До 7 додати 2 ‒ це означає додати 1 і ще раз 1. До 7 додамо 1 ‒ одержимо 8. До 8 додамо 1 ‒ одержимо 9. |
2 ‒ це 1 і ще 1. Від 8 відняти 2 ‒ це означає відняти 1 і ще раз 1. Від 8 віднімаємо 1 ‒ одержимо 7. Від 7 віднімаємо 1 ‒ одержимо 6. |
|
|
Додати 3 – означає додати 1 та ще 2, або додати 2 та ще 1. |
Відняти 4 – означає
|
|
|
Числа можна додавати і віднімати частинами |
||
|
6) додавання чисел 5, 6, 7, 8, 9 |
Теоретична основа додавання чисел 5, 6, 7, 8, 9 – переставний закон додавання. |
|
|
2 + 6 = Перший доданок 2, другий доданок ‒ 6. Незручно до меншого числа додавати більше, треба переставити місцями доданки (від перестановки доданків значення суми не змінюється): 2 + 6 = 6 + 2 = 8 |
||
|
7) віднімання чисел 6, 7, 8, 9 |
Теоретична основа віднімання чисел 6, 7, 8, 9 –взаємозв’язок дій додавання і віднімання. |
|
|
9 – 6 = Подати зменшуване у вигляді суми зручних доданків, один із яких дорівнює від’ємнику: 9 – 6 = 3 + 6 – 6 = Якщо від суми двох доданків відняти один доданок, то залишиться інший доданок. 9 – 6 = 3 + 6 – 6 = 3 |
||
|
|
|
|
|
|
Сума чисел Різниця чисел Математичний диктант Арифметичні дії додавання і віднімання Обчислення |
Для доповнення конспекту
Сума чисел - це число, яке отримується шляхом додавання двох або більше чисел.
Наприклад, сума чисел 5 і 2 дорівнює 7. Це означає, що якщо ми додамо 5 до 2, ми отримаємо 7.
Суму чисел можна записати різними способами. Наприклад, ми можемо написати:
- 5 + 2 = 7
- 2 + 5 = 7
- 7 = 5 + 2
- 7 = 2 + 5
Ми також можемо записати суму чисел на словах. Наприклад, ми можемо сказати:
- П'ять плюс два дорівнює семи.
- Два плюс п'ять дорівнює семи.
- Сім - це результат додавання п'яти і двох.
- Сім - це результат додавання двох і п'яти.
Різниця чисел - це число, яке отримується шляхом віднімання двох або більше чисел.
Наприклад, різниця чисел 5 і 2 дорівнює 3. Це означає, що якщо ми віднімемо 2 від 5, ми отримаємо 3.
Різницю чисел можна записати різними способами. Наприклад, ми можемо написати:
- 5 - 2 = 3
- 2 - 5 = -3
- 3 = 5 - 2
- -3 = 2 - 5
Ми також можемо записати різницю чисел на словах. Наприклад, ми можемо сказати:
- П'ять мінус два дорівнює трьом.
- Два мінус п'ять дорівнює мінус трьом.
- Три - це результат віднімання п'яти і двох.
- Мінус три - це результат віднімання двох і п'яти.
Математичний диктант - це форма контролю знань учнів, яка дає можливість одночасно і за короткий термін перевірити знання учнів усього класу.
Мета математичного диктанту:
- Повторення та засвоєння попереднього матеріалу, актуалізація й оцінювання рівня вивченого матеріалу.
- Розвиток умінь усних обчислень, швидкості реакції, концентрації уваги.
- Формування навичок самоконтролю.
Хід математичного диктанту:
- Учитель диктує приклади або задачі, а учні записують відповіді.
- Учитель може диктувати приклади або задачі по одному або по кілька штук за один раз.
- Учні можуть записувати відповіді в зошит або на дошку.
- Після диктанту учитель перевіряє відповіді учнів.
Види математичних диктантів:
- Додавання і віднімання. Учні записують відповіді на приклади додавання і віднімання.
- Множення і ділення. Учні записують відповіді на приклади множення і ділення.
- Рівняння. Учні записують відповіді на рівняння.
- Задачі. Учні записують відповіді на задачі.
Арифметичні дії додавання і віднімання - це основні арифметичні операції, які використовуються для обчислення результату двох або більше чисел.
Додавання - це операція, яка поєднує два або більше чисел в одне число.
Віднімання - це операція, яка вираховує різницю між двома або більше числами.
Основні відмінності між додавання і віднімання:
- Додавання - це операція, яка збільшує значення числа.
- Віднімання - це операція, яка зменшує значення числа.
- Додавання завжди дає позитивний результат.
- Віднімання може давати позитивний, негативний або нульовий результат.
Обчислення - це процес визначення значення математичної виразу. Обчислення можуть виконуватися вручну, за допомогою калькулятора або комп'ютера.
Основні види обчислень:
- Додавання - це операція, яка поєднує два або більше чисел в одне число.
- Віднімання - це операція, яка вираховує різницю між двома або більше числами.
- Множення - це операція, яка помножує два або більше чисел в одне число.
- Ділення - це операція, яка ділить одне число на інше.
1


про публікацію авторської розробки
Додати розробку