Методика викладання математики.

Методика викладання математики.

Вступ

В даний час, мабуть, немає необхідності доводити важливість математики у процесі викладання. Вона сприяють кращому формуванню окремих понять всередині окремих предметів, груп і систем, тобто таких, повне уявлення про які неможливо дати учням на уроках якої-небудь однієї дисципліни (поняття про будову матерії, різних процесах, видах енергії). 

Сучасний етап розвитку  математики як  науки характеризується взаємопроникненням наук один в одного, і особливо проникненням математики і фізики в інші галузі знання. 

Зв'язок математики як предмета є перш за все відображенням об'єктивно існуючої зв'язку з практичною діяльністю людей. 

Необхідність зв'язку між навчальними предметами диктується також дидактичними принципами навчання, виховними завданнями, зв'язком навчання з життям, підготовкою учнів до практичної діяльності.  Математика є конкретним виразом інтеграційних процесів, що відбуваються сьогодні в науці і в житті суспільства. Ці зв'язки грають важливу роль в підвищенні практичної і науково-теоретичної підготовки учнів, істотною особливістю якої є оволодіння школярами узагальненим характером пізнавальної діяльності. 

Математика допомагає формуванню в учнів цілісного уявлення про явища природи та взаємозв'язки між ними і тому робить знання практично більш значущими і застосовними, це допомагає учням ті знання і вміння, які вони придбали при вивченні одних предметів, використовувати при вивченні інших предметів, дає можливість застосовувати їх у конкретних ситуаціях, при розгляді приватних питань, як у навчальній, так і в позаурочній діяльності, наукової та громадської життя випускників.

За допомогою математики можна якісно вирішуються завдання навчання, розвитку та виховання учнів, але також закладається фундамент для професійного самовизначення учнів

1. Принципи і методи навчання математики

Важливе завдання процесу навчання математики це домогтися глибокого і міцного засвоєння учнями теоретичних знань: математичних понять, тверджень про їхні властивості (аксіоми, теореми), правил, законів; сформувати навички и уміння застосування теоретичних знань на практиці і оволодіння спо­собами творчої діяльності, досягти глибокого усвідомлення уч­нями світоглядних і морально-етичних цілей.

На сучасному етапі розвитку навчання трактується як цілеспрямований педагогічний процес організації і стимулювання активної навчально-пізнавальної діяльності учнів для оволодіння науковими знаннями, навичками - уміннями, роз­витку творчих здібностей, світогляду, морально-етичних поглядів і переконань. Процес навчання - двосторонній процес взаємодії між тим, хто вчить, і тим, хто навчається. Нагадаймо, що з курсу педагогіки закономірності процесу навчання, що об'єктивно існують, виступають як основні вимоги до практичної організації навчального процесу.

Як самостійну роботу пропонуємо інтерпретувати цей зміст на прикладах навчання математики. Враховуючи, що основна мета всебічний розвиток особистості, у процесі нав­чання математики треба спиратися і на дидактичні, і на психологічні принципи розвивального навчання. Дидактичні принципи розвивального навчання висунув у 60-70-х рр. Л. В. Занков. Він вважав, що не будь-яке навчання створює максимально сприятливі умови для розвитку учнів. Потрібний ретельний добір змісту, методів, організаційних форм і засобів навчання, щоб забезпечити ці умови. При цьому треба враховувати такі важливі дидактичні принципи розвивального на­вчання. Провідна роль теоретичних знань у процесі навчання мате­матики це означає, що не можна починати формувати уміння, навички застосування математичних знань доти, поки учні не засвоїли основні поняття, твердження, правила, закони, методи. Навчання швидкими темпами. У досвіді вчителів-новаторів (В. Ф. Шаталов, Р. Г. Хазанкін та ш.) реалізація цього принципу зводиться до вивчення основного теоретичного матеріалу швид­кими темпами на початку ознайомлення з темою, здійснення дійового контролю його засвоєння і звільнення цим самим часу для розв'язування задач. У процесі розв'язування задач теоретичний матеріал повторюється, поглиблюється, закріплюється.

Навчання на високому, але доступному рівні складності. Так само, як спортсмени розвивають свої фізичні можливості на вправах високої складності, учні повинні розвивати мислення, інтелект на навчальних задачах високого рівня складності. Цього принципу стосуються введені ще в 30-х рр. XX ст. психологом Л. С, Виготським поняття зони актуального і зони найближчого розвитку учнів. Учень працює в навчального матеріалу. Проте, як зазначав Л. С. Виготський, треба працювати на завтрашній день учня, тобто працювати в зоні його найближчого розвитку. Це означає, що учень має працювати над навчальними зонами актуального розвитку тоді, коли розв'язує навчальні задачі в межах засвоєного ним задачами, якщо він ще не спроможний розв'язати самостійно, але за незначної допомоги вчителя або своїх товаришів він таким задачам дає раду. Разом з тим об'єктивним фактом є те, що різні учні мають різні зони актуального  найближчого розвитку. Саме тому в умовах класно-урочної системи треба здійснювати рівневу диференціацію, використовувати групові и індивідуальні форми роботи, виділяючи групи учнів, які мають приблизно однаковий рівень загального розвитку, навченості, темпу просування у навчанні, цікавості до математики. Усвідомлення всіма учнями процесу навчання. Забезпечення цього принципу вимагає від учителя роботи з тими, хто не встигає, з'ясування причин цього та організації своєчасної педагогічної підтримки таких учнів.

Систематична робота викладача над загальним розвитком усіх учнів, у тому числі и найслабших. У процесі навчання матема­тики передусім передбачається розвиток мислення, оволодіння учнями загальними розумовими діями і прийомами розумової діяльності. Практика  дослідження психологів свідчить про те, що основною причиною того, що учні не встигають з математи­ки, є насамперед несформованність дій аналізу, синтезу, порівняння, абстрагування, узагальнення.

Психологічні принципи розвивального навчання:

1. Систематичний розвиток трьох основних видів мис­лення: наочно-дійове (або практичне), наочно-образне і абстрактно-теоретичне.

2. Проблемність навчання. Учень лише тоді включається в пізнавальний процес, виявляє розумову активність, коли стикається з проблемами (питаннями, задачами), які йому треба розв'язати.

3.Індивідуалізація і диференціація навчально-виховного про­цесу.

4. Цілеспрямоване формування алгоритмічних і евристичних прийомів розумової діяльності.

5. Систематичний розвиток мнемічної діяльності (тобто роз­виток пам'яті) для забезпечення фонду дійових знань.

На думку педагога і психолога П. П. Блонського, порожня голова не міркує. Психологи зазначають, що добре розвинена пам'ять - умова розвиненого інтелекту. У процесі навчання математики слід домагатися запам'ятовування учнями основних означень, тверджень, алгоритмів розв'язання ключових задач, озброювати учнів спеціальними мнемічними прийомами, які полегшують запам'ято­вування навчального матеріалу. Важливою є також спеціальна настанова вчителя на те, що тре­ба вивчити, перевести в довгострокову пам'ять, який матеріал вивчається для ознайомлення і не потребує заучування. Відсутність такого орієнтування призводить або до непотрібного перевантаження пам'яті учнів за сумлінного ставлення їх до навчання, або до ігнорування того, що треба вивчити, запам'ятати.

Слово «метод» грецького походження і в перекладі означає шлях дослідження, спосіб пізнання.

Під методом навчання в дидактиці розуміють способи навчальної роботи вчителя і організації навчально-пізнавальної діяльності учнів з розв'язування різних дидактичних задач, спрямованих на оволодіння матеріалом, що вивчається. Крім терміна «метод навчання» в дидактиці є термін «прийом навчання», під яким найчастіше розуміють складову частину або окремий бік методу.

Три методи використовують під час проблемного навчання як дидактичної системи. Проілюструємо застосування методів навчання математики за характером навчально-пізнавальної діяльності учнів.

Пояснювально-ілюстративний     Цим методом послуговуються, вводячи математичні поняття, вивчаючи аксіоми, теореми способи розв'язування різних класів задач.

Репродуктивний   Використовують при поясненні нового матеріалу, перевірки домашнього завдання (учні відтворюють розв'язання задач, формулювання і доведення теорем, означення математичних по­нять, правила тощо). На уроках, де формуються уміння і навички розв'язування прикладів, задач, застосування репродуктивного методу виявляється в діяльності учнів під час розв'язування вправ і задач за зразком, який дано викладачом або наведено в підручнику, в діяльності за певним алгоритмом. При цьому діяльність за зразком має проводитись не за вказівкою «роби те, що роблю я», а за порадою «роби так, як роблю я». Недоліком двох названих методів є те, що вони мало сприяють розвитку продуктивного мислення, пізнавальної активності и самостійності учнів. Разом з тим недооцінка репродуктивної діяльності учнів призводить до того, що в учнів не забезпечується фонд  знань, який є необхідною умовою для можливостей організації самостійної пізнавальної діяльності, розвитку творчого мислення і продуктивної діяльності.

Наступні три методи проблемного навчання спрямовані на усунення зазначених вище недоліків.

Проблемний виклад як метод навчання математики -  полягає в тому, що, пояснюючи навчальний матеріал, викладач сам висуває проблеми і, звичайно, як правило, сам їх розв'язує. Однак постановка проблем посилює увагу учнів, активізує процес сприймання і усвідомлення того, що пояснює вчитель.

Частково-пошуковий метод    (його інколи називають евристичною бесідою) полягає в тому що вчитель заздалегідь готує систему питань, відповідаючи на які учні самостійно формулюють означення поняття, «відкривають» доведення тео­реми, знаходять спосіб розв'язування задачі.

Дослідницький  метод передбачає  самостійний пошук розв'язання пізнавальної задачі. Причому може виявитись потреба, щоб проб­лему  сформулював сам  учень  або  и  формулює вчитель,  але розв'язують учні самостійно.

Метод доцільних задач     запропонував   наприкінці   XІX   ст. Шохор-Троцький. Належить він фактично до методів проблемного навчання. Навчання математики згідно з цим методом здійснюється за допомогою задач. Із задач починається вивчення будь-якої теми, що, природно, забезпечує мотивацію вивчення теоретичного матеріалу. Вивчаючи теоретичний матеріал теми, учні переважно розв'язують задачі. Теореми в геометрії доводять лише ті, які для учнів не є очевидними, але і не потребують надто тонких міркувань. Практика засвідчила, що значення методу доцільних задач не можна перебільшувати і додержуватися його формально. По-перше, вивчення не кожної теми доцільно починати з розв'язування задач, по-друге, не можна недооцінювати роль теоретичних знань.

Суть абстрактно-дедуктивного методу навчання полягає в то­му, що під час вивчення нового матеріалу викладач відразу сам повідомляє означення понять, що вводиться, а потім наводить конкретні приклади об’єктів, що належать до понять. Формулюється и доводиться теорема, і лише після цього розглядаються конкретні приклади застосування нового теоретичного матеріалу.

Конкретно-індуктивний метод навчання протилежний абстракт­но-дедуктивному методу. Під час навчання цим методом пояс­нення нового матеріалу починається з розгляду прикладів. Використовуючи приклади, учні мають можливість виділити суттєві ознаки  поняття,  що  вводиться.  Це допомагає  самостійно  чи з допомогою вчителя сформулювати означення поняття. Рисунок до теореми дасть змогу учням виявити властивості зображеної фігури і самостійно чи з допомогою вчителя сформулювати теорему. Поряд з усним викладом теоретичних знань, поясненням учи­телем способів розв'язування різних типів задач та колективним їх розв'язуванням значне місце в процесі навчання математики посідає самостійна робота учнів. До самостійної роботи можна віднести самостійне вивчення учнями навчального матеріалу на уроці або під час виконання домашнього завдання за підручниками, навчальними посібниками та науково-популярною літературою, самостійне доведення теорем та розв'язування задач, робо­ту в зошитах з друкованою основою, програмоване навчання за допомогою програмованих посібників та персональних комп'ютерів.

Самостійна робота учнів за підручником, навчальними посібниками, науково-популярною літературою - важливий для самоосвіти прийом навчальної роботи, якому необхідно спеціально цілеспрямовано навчати учнів як в основній, так і в старшій школі.

Нові знання з математики сприймаються і засвоюються учня­ми з певними труднощами. Тому потрібні поради вчителя щодо роботи над математичним текстом. Вони можуть мати вигляд такого правила-орієнтира.

1. Прочитай уважно текст один чи два рази, виділи головне в ньому (нові поняття, твердження, правила тощо).

2. Склади план прочитаного.

3. Види поняття, про які йдеться в тексті. Пригадай означення відомих понять і види означення нових.

4. Виділи твердження, які доводяться в тексті. З'ясуй, що в них дано, що треба довести. З'ясуй, з яких тверджень складається доведення, за допомогою яких відомих тверджень вони обгрунтовується.

5. Спробуй відповісти на контрольні запитання. Сформулюй означення нових понять і твердження, які доводились в тексті.

6. Не вдаючись до тексту, виконай потрібні рисунки і відтвори прочитане за планом.

Програмоване   навчання   виникло  з   потреб вдосконалення традиційного навчання і створення кращих умов для реалізації дидактичних принципів навчання. Термін «програмоване навчання» походить від термінів програмування для ЕОМ і здійснюється за навчальними програмами. У них матеріал, що вивчається, подається послідовними     порціями, після засвоєння кожної з яких учням пропонується контрольне запитання або завдання. Перехід до наступної порції допускається лише після ознайомлення з правильною відповіддю і характером помилки, якої учень припустився. Існує дві системи програмування навчального матеріалу - лінійні та розгалужені програми.

Домашні завдання - це один з видів самостійної роботи, який звичайно може включати як закріплення  вивченого на  уроці,  так  і самостійне вивчення нового навчального матеріалу за підручником, розв'язування вправ та задач за зразком і таких, що мають певну новизну і вимагають від учнів творчого підходу до застосування знань. Домашнє завдання дає змогу зосереджувати процес усвідомлення і запам'ятовування головного в навчальному матеріалі.

Під час повторення навчального матеріалу корисно іноді за­пропонувати учням навести свої приклади замість тих, що наводяться в підручнику.

2. Внутрішньопредметні та міжпредметні зв’язки. Професійне спрямування викладання математики.

Потреба реалізації внутрішньопредметних зв'язків випливає з дедук­тивного характеру математики і визначається тим, що оволо­діння системою знань є водночас і засобом, і метою розвитку особистості учня. Психологи Ю. О. Самарін, П. О. Шеварьов переконливо по­казали системний характер розумової діяльності школярів, що здійсню­ється через узагальнення асоціативних зв'язків, включення їх у зв'язки вищого порядку. З реалізацією внутрішньопредметних зв'язків тісно пов'язана проблема наступності в навчанні. У «Педагогической энциклопедии» зазначається, що наступність у навчанні полягає в установлен­ні потрібного зв'язку і правильного співвідношення між частинами на­вчального предмета на різних ступенях його вивчення . У педагогі­ці знаннями вважають не будь-яку інформацію, а лише ту, яка має якість системності, тобто якість знань, що характеризує наявність у сві­домості учня структурних зв'язків або зв'язків будови знання всередині наукової теорії. Маються на увазі зв'язки між поняттями, твердження­ми, способами розв'язування задач та ін. Тому потрібна цілеспрямована систематична робота вчителя для встановлення зв'язків і відношень між різними елементами знань.

Враховуючи концентричний характер побудови програми з мате­матики, слід забезпечити єдиний підхід у трактуванні понять, спосо­бах діяльності учнів і обов'язкову опору на вже засвоєні учнями знання. Наприклад, вивчаючи геометричні величини в систематично­му курсі геометрії, важливо актуалізувати ті уявлення, знання та на­вички, які учні здобули.

Під час засвоєння понять слід показувати учням зв'язки «рід - вид», вивчаючи різні множини чисел, види виразів в алгебрі, чотири­кутники в геометрії тощо, використовувати класифікаційні схеми.

Реалізації внутрішньопредметних зв'язків сприяє використання ана­логій у процесі навчання математики. Наприклад, у стереометрії визна­чення багатьох понять формулюються аналогічно спорідненим поняттям планіметрії. Крім того, розв'язування більшості стереометричних задач зводиться до планіметричних. Тому важливо, з одного боку, забезпечити свідоме і міцне засвоєння головного у планіметрії, а з другого - систе­матично повторювати цей матеріал і вміло актуалізувати його з метою вивчення відповідного матеріалу зі стереометрії.

Міжпредметні зв'язки. Зв'язки між елементами знань і умінь з різних навчальних предметів сприяють формуванню всебічно розви­неної творчої особистості, яка оволоділа системними знаннями, загальнонауковими уміннями та навичками і вміє застосовувати міжпредметне перенесення знань й умінь для розв'язування нових пізна­вальних задач. Міжпредметні зв'язки є визначальними у вирішенні проблеми інтеграції та координації навчання.

Інтеграція - це процес і результат створення нерозривно по­в'язаного, єдиного, суцільного. Нині ця проблема актуальна для шко­ли у зв'язку зі створенням інтегрованих курсів (математика з інфор­матикою, природознавство, суспільствознавство). І в нашій країні, і в зарубіжних системах освіти давно ставилося завдання створення єди­ного інтегрованого курсу математики, не розділеного на предмети - алгебру, геометрію, алгебру і початки аналізу. У Німеччині такий курс існує традиційно. У Болгарії група вчених під керівництвом Б. Сендова вже створила підручники для кількох класів, які інтегрують ма­тематику, рідну й іноземну мови та інші предмети.

Координація - це погодження навчальних програм зі спорідне­них предметів з погляду єдиного підходу до трактування понять, ідей, методів, процесів, явищ, а також у часі їх вивчення.

Міжпредметні зв'язки реалізуються поєднанням інтеграції та коор­динації знань, які взаємно доповнюються і сприяють формуванню в учнів єдиної картини світу, наукового світогляду. Міжпредметні зв'язки спрямовані на надання учням системи політехнічних знань зі споріднених предметів: математика - фізика - хімія - біологія - фізич­на географія - креслення - трудове навчання.

Реалізація міжпредметних зв'язків має здійснюватися передусім за допомогою використання математичних ідей і методів, математичного апарату в інших предметах, розгляду в курсі математики навчального матеріалу, який має велике значення в споріднених дисциплінах. Важ­ливо також приділяти достатню увагу тому, як математичні задачі виникають на основі задач з інших предметів і як метод розв'язування цих математичних задач використовується для розв'язування нематематичних задач. Реалізувати міжпредметні зв'язки під час вивчення математики означає насамперед створити запас математичних моделей, які описують явища і процеси, що вивчаються в різних предметах. Такими моделями є основні поняття математики: величина, число, функція, фігура, рівняння, похідна, інтеграл, диференціальне рів­няння, ймовірність тощо. Наприклад, похідна - це математична модель різних фізичних, хімічних, біологічних понять: швидкості прямолінійного нерівномірного руху, електрорушійної сили, індукції як швидкості зміни магнітного потоку у фізиці, швидкості реакції в хімії, швидкості розмноження бактерій у біології та ін. До мате­матичних моделей прикладних задач належать такі важливі мате­матичні задачі: знаходження розв'язку алгебраїчного рівняння; най­більшого і найменшого значення функції; розв'язку диференціального рівняння, що задовольняє певні початкові умови; формування закону розподілу деяких випадкових величин.

Можна назвати основні напрями зв'язків математики з фізикою: величини та їх вимірювання; обчислювальна культура; функції та графіки, похідна, інтеграл, диференціальні рівняння; вектори.

Найістотніші зв'язки математики з хімією виникають під час роз­в'язування задач на пропорції, проценти, використання правил набли­жених обчислень. Аналіз навчально-методичної літератури і стану на­вчання хімії та фізики в школі й педагогічному вищому навчальному закладі свідчить, що найсуттєвіші прогалини в обчислювальній культурі пов'язані з наближеними обчисленнями. Тому виникає потреба в тісних зв'язках у роботі вчителів математики, хімії та фізики, зокрема у прове­денні методичних об'єднань з цих питань, участі вчителів математики в опрацюванні результатів вимірювань і обчислень під час проведення ла­бораторних робіт і уроків з розв'язування обчислювальних задач.

Слід мати також на увазі, що деякі математичні поняття на уроках фізики і хімії запроваджуються раніше, ніж на уроках математики. Тому, по-перше, потрібно забезпечити єдиний підхід до трактування таких понять і, по-друге, на уроках математики використовувати вже відомі учням знання. Прикладом є поняття стандартного вигляду чис­ла. На уроках фізики і хімії учнів підводять до цього поняття по-різ­ному. Зокрема, в § 7 підручника з неорганічної хімії авторів Г. Є. Рудзітіса, Ф. Г. Фельдмана йдеться про те, що маса малого легкого атома Гідрогену становить 0,000 000 000 000 000 000 000 000 001 663 кг, або 1,66-10²⁷ кг, або 1,66-10 г. Маса атома Оксигену становить 2,66-10 кг, а маса атома Карбону -2,0-10" кг. У курсі фізики вже в 7 класі виникає потреба ввести стандартний вигляд числа. Про­те автори підручника з фізики  подають це питання так: най­меншу масу має молекула водню; її маса дорівнює 0,000 000 000 000 000 000 000 003 3 г.

Зв'язки математики з кресленням навчанням спрямова­ні на формування графічної грамотності учнів, що відбувається під час вивчення комплексу предметів - математики, креслення, образо­творчого мистецтва, географії, фізики, хімії, трудового навчання. На цих уроках учні ознайомлюються з різними графічними зображення­ми: рисунками, кресленнями, ескізами, географічними картами, схе­мами, графіками, діаграмами тощо. Проте креслення як предмет є основним у системі графічної підготовки учнів

Під час вивчення курсу геометрії потрібно спиратися на знання й уміння, отримані на уроках праці.

Уже на перших уроках креслення у 8 класі слід звернути увагу учнів на те, що наочні зображення, виконані від руки «на око», без точного дотримання розмірів предмета, називають технічним рисун­ком, що лінії, паралельні па предметі в натуральному вигляді, залиша­ються паралельними і на зображенні. Ці зауваження стосу­ються також геометричного рисунка і є підготовкою до вивчення влас­тивостей паралельної проекції в курсі геометрії  та правил зображення просторових фігур на площині.

Важливим напрямом зв'язку геометрії та креслення є єдиний під­хід до використання ліній і позначення літер, розмірів фігур відповід­но до чинних стандартів Єдиної системи конструкторської документа­ції (ЄСКД).

Наведемо вимоги до використання ліній у зображеннях, з якими учні ознайомлюються на уроках креслення і мають дотримуватися в геометрії.

Суцільна товста основна лінія призначена для зображення видимих контурів, предметів. її товщину вибирають від 0,5 до 1,4 мм залежно від розмірів і складності зображень, форми рисунка і позначають літерою 5.

Штриховою лінією зображають невидимі контури предметів. Дов­жину кожного штриха вибирають від 2 до 8 мм залежно від розмірів зображення. Відстань між штрихами в лінії має дорівнювати 1-2 мм і бути приблизно однаковою на всьому зображенні. Товщина штрихо­вих ліній становить від 5/3 до s/2.

Суцільну тонку лінію завтовшки від 5/3 до 5/2 використовують для неповного зображення, наприклад у разі зображення площини у вигляді обірваного контуру.

У гео­графії вводяться поняття лінійного масштабу, іменованого масштабу, відносної й абсолютної висоти. Останні два поняття доцільно викори­стати, розглядаючи від'ємні числа. Наприклад, відносний рівень (ви­сота) води в річці може виражатись як додатним, так і від'ємним чи­слом.

Задачі на визначення масштабу знімання можуть розв'язуватися не тільки на уроках географії, а й на уроках математики. Наведемо при­клад такої задачі.

Задача 1.1. Нехай потрібно зобразити на аркуші шкільного зошита розміром 21x17 см вулицю завдовжки 1 км. Зображення вулиці має вміститися на ньому і може мати довжину не більш як 20 см. Який масштаб слід узяти?

Розв'язання. Досить розділити довжину вулиці (1 км) на довжину відрізка, що її зображає (20 см). Маємо:

Це означає, що на плані довжина вулиці зменшиться в 5000 разів. Отже, чис­ловий масштаб - = 1 : 5000, а іменований - в 1 см міститься 50 м.

Учні дізнаються, що дуги кола вимірюються в градусах, на уроках географії, тобто до того як починають вивчати геометрію. Водночас ставиться завдання обчислити в метрах довжину дуги кола (меридіа­на) в Г. У цьому разі міркування такі. Довжина кола Землі становить 40 000 км, а півкола - 20 000 км. Півколу відповідає дуга в 180°. Тому 20000:180= 111 км (наближено). Знаючи це, за градусами меридіанів можна обчислювати відстані в кілометрах.

На жаль, у згаданому підручнику географії ціла низка понять вво­диться некоректно з погляду математики. Наведемо два приклади.

1. У зв'язку з введенням лінійного масштабу стверджується: «Мас­штаб - це пряма лінія, розділена на рівні частини (звичайно сантимет­ри)». Проте пряма лінія - нескінченна, отже, її не можна розділити на рівні частини [79, 15]. Очевидно, йдеться про відрізок, а не про пряму.

2. У зв'язку із введенням понять паралелі, меридіана та їхніх вла­стивостей наводиться таке означення: «Паралелями називають лінії, умовно проведені на поверхні Землі паралельно екватору». Однак екватор, як і паралель, - коло, а поняття паралельності застосовне лише для прямих. Далі читаємо: «Як і меридіан, паралель можна провести через будь-яку точку земної поверхні. У кожній точці пара­лель перпендикулярна до меридіана» [79, 23]. Проте відношення пер­пендикулярності також застосовне лише для прямих, а кут між кри­вими, якими є паралель і меридіан, - це кут між дотичними, прове­деними до кривих у точці їх перетину.

Взаємозв’язок математики зі спецпредметом

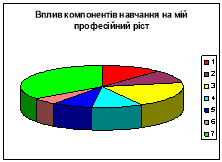      На превеликий жаль, програми з математики і спецдисциплін не завжди співпадають у часі, тому зв'язок математики з професією доводиться здійснювати на бінарних, інтегрованих, навчальних уроках з використанням випереджаючих завдань, позакласних заходах. Доцільно завершувати викладання кожного розділу калейдоскопом математичних прикладних задач. Досліджуючи вплив компонентів навчання на професійний ріст учня, отримали таку діаграму.

1-математика;
2- інші науки;
3 - спецдисципліни;
4 - навчальні екскурсії;
5 - практичні роботи;
6 - дослідницькі роботи;
7 - виробнича практика.

Як бачимо, знання математики у вивченні спецдисциплін займають важливе місце у професійному становленні учня. Це ще раз підкреслює актуальність думки Леонардо да Вінчі: «Ніяке людське дослідження не може бути назване істиною, якщо воно не проходить через математичні доведення».

Математика тісно взаємозв’язана з фізіологією харчування, а саме  визначення загальної кількості калорій, необхідних на день (робота з таблицею). Зразкові енерговитрати при різних видах роботи (дані наведені в ккал / год на 60 кг маси тіла).

Для розрахунку добових енергетичних витрат перемножте час (в годинах) тієї чи іншої діяльності на кількість енергії, яка при цьому витрачається. Нормальним вважається, якщо калорійність харчового раціону людини перевищує енерговитрати не більш, ніж на 5%. 

2. Складання харчового раціону. Розраховують харчовий раціон в залежності від енерговитрат. Для цього спостерігають свій енергообмін протягом декількох днів і визначають середні дані. Складають добовий раціон харчування з того розрахунку, що кількість білків, жирів, вуглеводів, необхідних на добу, має приблизно відповідати співвідношенню 1:1:4, і що в добу підліткам 15-16 років необхідно приблизно 10 - 120 г білків, 90 - 110 г жирів, 450 - 500 г вуглеводів. Треба пам'ятати, що в раціоні має бути достатня кількістьвітамінів, мікроелементів. 

Використовуючи табличні дані про калорійність різних продуктів, учні складають меню чотириразового харчування так, щоб на сніданок, обід, полуденок і вечерю доводилося відповідно 25%, 50, 15, 10% добового раціону. Результати розрахунків заносять у таблицю.

У житті   повинно забезпечувати  складання раціону, підбір оптимальних дієт (до речі, дієту повинен становити професіонал, інакше можна нашкодити своєму здоров'ю). Ця професія стала актуальною і затребуваною в даний час, так як намітилася стійка тенденція: люди все більше звертають увагу на своє здоров'я, свій зовнішній вигляд. 

3. Формування математичних  понять.

Процес означення математичних понять - це процес зведення означуваного поняття до другого, з більш широким обсягом, дру­гого - до третього з ще ширшим обсягом і т. д. Оскільки такий процес не може бути нескінченним, виникає потреба у первісних поняттях, яким не дається означення.

У шкільному курсі математики до таких понять належать по­няття: натуральне число, множина, точка, пряма, площина, відношення «належати», «лежить між», довжини відрізка, градусної міри кута.

Хоч первісні поняття не означаються явно через інші поняття, проте іх зміст розкривається через систему аксіом. Наприклад, в аксіомах планіметрії розкриваються основні властивості первісних понять - точки, прямої тощо. Тому систему аксіом розглядають як неявне, непряме означення первісних понять.

Систематизація і класифікація навчального матеріалу, зокрема математичних понять, допомагають учням глибше усвідомити зв'язки між поняттями, їхніми властивостями і відношеннями, чіткіше уявити структуру навчального матеріалу і математики в цілому. Усвідомлення системи математичних понять, суджень і умовиводів особливо важливе в разі дедуктивної побудови теорії, насамперед шкільного курсу геометрії.

Система (від грецьк. - ціле, складене з частин) - сукупність, об'єднання взаємопов'язаних і розташованих у певному порядку елементів (частин) якого-небудь цілісного утворення.

Систематизація - розміщення матеріалу в пев­ному порядку, певній послідовності. Наведемо приклад застосування систематизації в разі формування поняття графіка лінійного рівняння ах + Ьу = с.

Систематизацію навчального матеріалу зручно подати у формі таблиці Аналізуючи таблицю, в якій систематизовано весь навчальний матеріал, можна помітити, що графіком лінійного рівняння з двома невідомими є пряма тоді і лише тоді, коли хоча б один з коефіцієнтів а чи в не дорівнює 0; якщо а = О, Ь = 0, то графіком є порожня множина точок, а коли всі параметри одночасно дорівнюють 0, графіком є множина всіх точок координатної площини.

Класифікація (від лат. розряд, - роблю) - розподіл об’єктів за класами, залежно від їх загальних ознак. У термінах теорії множин класифікація - це розбиття множини об’єктів на підмножини, які не перетинаються.

Ознаку, за якою здійснюється поділ поняття, називають осно­вою поділу. Обсяг одного и того самого поняття можна ділити на підмножини по-різному залежно від обраної основи. Наприклад, якщо в основу класифікації трикутників покласти величину кута, то трикутники можна поділити на гострокутні, прямокутні, тупокутні, а якщо - співвідношення між сторонами, то множину трикутників можна поділити на дві підмножини - різносторонні три­кутники і рівнобедрені трикутники. Засвоєння математичних понять відбувається формуванням понять у процесі аналітико-синтетичної діяльності учнів, спрямованої на виділення суттєвих загальних властивостей певного поняття і усвідомлення несуттєвих властивостей, а також на застосування нового поняття до розв'язування задач. У структуру пізнавальної діяльності учнів щодо засвоєння математичних понять входять як загальні (аналіз, синтез, порівняння, абстрагування, узагальнення тощо), так і специфічні розумові дій (дій підведення під поняття і обернена їм дія - виведення наслідків). Коли вивчаються паралельні прямі в планіметрії, то, виділяючи (аналіз) пари прямих, учні порівнюють їх і після з'ясування суттєвого спільного в парах об'єднують (синтез) пари за цими спільними суттєвими властивостями, відволікаючись від несуттєвого в них (відстань між прямими, їх розташування на площині) (абстрагування). На стадії введення терміна і символу закінчується узагальнення при формуванні поняття «паралельні прямі». Коли використовується абстрактно-дедуктивний метод навчання при формуванні нового поняття, вчитель формулює означення сам, наводить приклади об’єктів, що належать до цього поняття, виділяє суттєві спільні властивості і зазначає несуттєві. Наприклад, вводячи поняття «тотожно рівні вирази», вчитель повинен сам сформулювати означення (два вирази, відповідні значення яких рівні за будь-яких значень змінних, називають тотожно рівними) і навести приклади тотожно рівних виразів і таких, які не є ними. Суттєвою спільною властивістю тотожно рівних виразів є рівність їхніх відповідних числових значень за будь-яких однакових значень змінних. Несуттєвим є кількість змінних, що входять до виразу, форма виразів. Труднощі засвоєння понять учнями, які слабко встигають, пояснюються передусім невмінням виділяти суттєві властивості об’єктів і абстрагуватись від несуттєвих.

У зв'язку з цим учні роблять неправомірні узагальнення або, іншими словами, генералізацію несуттєвих властивостей (надання їм ролі суттєвих). Суттєвими для них стають яскраві властивості, які виступають на перший план саме тоді, коли фігури розміщені на рисунку стан­дартно. Ще один приклад. Окремі учні вважають, що зовнішній кут трикутника завжди тупий, більший за внутрішній, суміжний з ним. Така ситуація складається, коли вчитель обмежується прикладами лише гострокутних трикутників.

4. Вимоги до комплексно-методичного забезпечення

Комплекс навчально-методичного забезпечення з математики складається з:

1) навчальної документації: навчальний план; навчальна програма; комплект перспективно-тематичних планів з усіх тем предмета; лани уроків; перелік навчально-виробничих робіт з професії тощо;

2) навчальних засобів для учнів: підручники; навчальні посібники; конспекти лекцій, підготовлені викладачами; довідники; збірники задач і завдань для вправ і самостійних робіт; комплекти інструкційно-технологічної документації тощо;

3) дидактичних засобів на урок: природні та зображувальні наочні приладдя;

технічні засоби навчання; демонстраційне обладнання; програмне забезпечення для комп’ютерної техніки; дидактичні матеріали тощо;

В умовах оновлення змісту професійної освіти важливого значення набуває розробка та впровадження в навчальний процес новітніх підручників, посібників, методик викладання, нового парку обладнання, комп’ютерної та електронно-обчислювальної техніки тощо.

Підвищення рівня вимог до обсягу базових знань кваліфікованих робітників зумовлюють необхідність інтенсифікації процесу навчання.

А це можливо лише за умови успішного розв’язання проблеми науково-методичного забезпечення навчально-виховного процесу в навчальному закладі. Правильно організоване науково-методичне забезпечення системи занять з кожної дисципліни дозволяє підвищити інформаційну насиченість навчального матеріалу, забезпечує наочність, розширює можливості для самостійної пізнавальної діяльності учнів і активізує їхнє мислення; дозволяє досягнути інтегрального результату педагогічної діяльності викладача.

Висновки та пропозиції

Реалізація ідеї викладання тісно пов'язано з методологічними поглядами педагогів на проблему синтезу і аналізу наукового знання як конкретного вираження диференціації наук. Теоретичне та практичне розв'язання цієї проблеми змінювалося відповідно до розвитку суспільства, його соціальним замовленням педагогічної науки і школі. Утвердження і зміцнення предметної системи викладання в сучасному житті нерозривно пов'язане з розвитком ідеї. 

Виявлення і подальше здійснення необхідних і важливих для розкриття провідних положень навчальних тем дозволяє: 

знизити ймовірність суб'єктивного підходу у визначенні у визначенні навчальних тем. 

зосередити увагу викладачів і учнів на вузлових аспектах предмету, який відіграє важливу роль в розкритті провідних ідей наук. 

здійснювати поетапну організацію роботи щодо встановлення ускладнюючих та пізнавальних завдань, розширюючи поле дії творчої ініціативи та пізнавальної самодіяльності учнів, застосовуючи все різноманіття дидактичних засобів 

формувати пізнавальні інтереси учнів засобами навчальння в їх органічній єдності. 

здійснювати творчу співпрацю між викладачем та учнями. 

вивчати найважливіші світоглядні проблеми і питання сучасності з засобами науки та зв'язку з життям. 

Поліпшення системи багатосторонніх зв'язків передбачає і подальше вдосконалення шляхів їх реалізації:  планування та поєднання роботи, координацію діяльності всіх учасників педагогічного процесу; ефективне використання  екскурсій, конференцій, розширення практики здвоєних уроків, на яких можуть вирішуватися вузлові світоглядні проблеми з засобами навчання.

                                 Список використаної літератури
1. Смирнова М.А. Теоретичні основи міжпредметних зв'язків - М., 2006. 
2. Міжпредметні зв'язки в навчальному процесі. / Під. ред. Дмитрієв С.Д. -Кіров - Йошкар-Ола: Кіровський держ. пед. ін-т, 1978 - с.80. 
3. Лошкарьова Н.А. Міжпредметні зв'язки як засіб удосконалення навчально-виховного процесу - Вип.5. - М.: МГПИ ім.В.І.Леніна, 1981.; Лошкарьова Н.А. Про поняття і види міжпредметних зв'язків / / педагогіка. - М., 1972. - № 6 - С.48-56.

4. Закон України “Про загальну середню освіту ”, Київ, 1999р.

5. Державна національна програма “Освіта/Україна ХХI століття/Заходи щодо реалізації Державної національної програми “Освіта/Україна ХХI століття/Затверджено постановою Кабінету Міністрів України від 03.11.93 №896//Освіта – 1993 - №44-46

6. Слєпкань З.І. Методика навчання математики. – К.: Зодіак-ЕКО, 2000р. – 512с.

7. Єременко І.Г. Олігофренопедагогіка. - К.: Вища школа, 1985.

8. Есипов Б.П. Самостоятельная работа учащихся на уроках. -М: Учпедгиз, 1961.

9. Книга для учителя вспомогательной школы / Под ред. Г.М.Дульнева.- М.: Учпедгиз, 1959.

10. Основи спеціальної дидактики / За ред. І.Г.Єременка. - К.: Ра­дянська школа, 1975.

11. Перова М.Н. Методика преподавания математике в специальной (коррекционной) школе VIII вида. - М.: Владос, 1999.

12. Печерский В.Г. Программированные задания как способ организации учебной деятельности учащихся коррекционной школы // Дефектология. - 2000. - №1. - С. 44-47.

13. Прахина М.П. Практическая направленность преподавания ма­тематики во вспомогательной школе // Дефектология. - 1991. - №5. -С.34-37.

Додаток 1

Тригонометричні функції

Задача 1

Дуга кругового сектора переднього колеса трактора МТЗ - 80 становить 0,94 радіан. Обчислити площу сектора, якщо радіус колеса цього трактора дорівнює 0,46 м.

Задача 2

Знайти радіус колеса трактора Т-150 К, якщо його дуга довжиною 0,80м містить 1,5 радіан.

Задача 3

Круговий сектор заднього колеса трактора, що має площу 0,39 метрів квадратних стягується дугою  в 1,4 радіан. Знайти радіус колеса.

Задача4

Чотири точки ділять коло колеса трактора Т-150 у відношенні 3:4:5:6.

Обчисліть в радіанній мірі величини відповідних дуг.

Задача 5

Слюсар при закріпленні деталі в лещата повернув важіль лещат на 270 градусів. Яку дугу описав при цьому кінець важеля, якщо довжина важеля від центра 7,5 см.

Похідна та її застосування

Задача 1

Обчислити розтрату бензину при швидкості руху 50, 80, 100 км\год і найбільшу економічну швидкість автомобіля.

Задача 2

Об’єм башти циліндричної форми 27 м3 . Яке повинно бути відношення між радіусом основи і висотою, щоб повна поверхня (з кришкою) була мінімальною.

Задача 3

Для зберігання солярки використовують цистерни циліндричної форми. Знайти розміри цієї цистерни із заданим об’ємом V і найменшою повною поверхнею.

Задача 4

Для зберігання мінеральних добрив побудовано склад, внутрішній периметр якого не перевищує 80м. Яких розмірів повинно бути приміщення складу щоб площа підлоги була найбільша?

Показникова і логарифмічні функції

Задача 1

Фермер купив новий інвентар (сівалки, культиватори) для обробітку ґрунту на суму 35 тис. грн. Яка буде вартість цього інвентарю через рік, два роки, шість років коли щороку на амортизацію відраховують 10% його вартості.

Обчисліть вартість інвентарю через 6 років.

Задача 2

Для внесення мінеральних добрив придбали 2 тис кг. Але всередньому щорічно втрачається до 1,5% добрив (на складах, в розкидачах, випаровується). Обчислити витрату добрив за 1рік, 2 роки, за 5 років.

Задача 3

В тваринницькій сфері с\г промисловості заплановано щорічний приріст на 3%. Визначити об’єм продукції в ці сфері через 5,10,12 років.

Аксіоми стереометрії

Задача 1

При зніманні гільз циліндрів в моторі трактора використовують знімач який стоїть на трьох ніжках. На якому положенні обґрунтовується ця операція.

Задача 2

При яких положеннях головка важеля керування, ківш і направляюче колесо гусениці екскаватора знаходяться в одній площині.

Задача 3

На рамі ходової частини колісного трактора лежать відрізки АБ, СД, які перетинаються в т.м. Доведіть що прямі АС, БД, БС, АД лежать у площині рами.

Паралельність прямих і площин

Задача 1

Стоянка тракторів знаходить на відстані 7,5 км ві поля 4,5 км від шосейної дороги, яка розміщена паралельно до поля. Від стоянки до поля пролягає ґрунтова дорога, довжина якої до шосейної дороги 6,5 км. Знайти відстань по ґрунтовій дорозі від поля до стоянки.

Навести приклади паралельних площин в конструкції сівалки.

3. Навести приклади мимобіжних паралельних прямих, що перетинаються в конструкції комбайна.

4. Як повинна бути розміщена рама плуга відносно землі, для того щоб всі корпуси орали на одну глибину.

Перпендикулярність прямих і площин

1. Назвати деякі деталі комбайна, які знаходяться в перпендикулярних площинах.
2. Довести що бічне ребро кузова трактора перпендикулярне до його основи

Задача

Плита регулювання пальцевого механізму шнека жатки комбайна є квадрат із стороною 17 см. З центра квадрата проходить вал довжиною 3 м. перпендикулярно до площини квадрата. Знайдіть відстань від кінця валу до вершини квадрата.

Многогранники

1. Надсічена частина трьохгранного рашпілю шириною 20мм. нанесена по довжині 250мм. Визначити бічну поверхню бічної частини.

2. Бак прямокутного перерізу 3,2х1,2м. вміщує 9 тис. л. води. Скільки метрів квадратних пішло на його виготовлення.

3. Підшипник соломо набивача зернозбирального комбайна є прямокутним паралепіпедом площа поверхні якого дорівнює 470 метрів квадратних. Сторони основи 15х5см. Знайдіть висоту підшипника.
4. Верх башти має вид правильної шестикутної піраміди сторона основи 2м., висота 12,2м. Знайти поверхню верха башти.

Площі поверхонь тіл обертання

1. Зонт самохідного комбайна має форму сферичного сегмента. Визначити поверхню зонта, якщо його висота і радіус основи відповідно дорівнюють 25 і 75 см.
2. Ролик підшипника кочення маю форму циліндра, висота якого 20 см., а діаметр основи 10мм. Визначити площу поверхні ролика.
3. Стіжок сіна має форму циліндра з конічним верхом. Висота циліндричної частини 2,4м., радіус основи стіжка 2,4мм, а висота стіжка 4,4м. Скільки поліетиленової плівки потрібно, щоб повністю накрити стіжок.

Тіла обертання

1. Купа піску має форму конуса, радіус основи 28дм. Твірна більша від висоти конуса на 8дм. Знайдіть площу осьового перерізу піску.
2. Більший діаметр ролика конічного підшипника дорівнює 60 см., висота 200мм. Визначити менший діаметр ролика підшипника, якщо відношення більшого діаметра до його висоти дорівнює 1:10.
3. Силосна башня має форму циліндра діагональ осьового перерізу якого дорівнює 14мю і нахилена до площини основи під кутом 30. Знайдіть радіус основи і висоту башти