Методика вивчення числових нерівностей і їх властивостей у шкільному курсі математики
1.Місце теми: «Числові нерівності» у програму. Основна мета вивчення, державні вимоги до рівня загальноосвітньої підготовки учнів.
2.Введення поняття числової нерівності.
2.1. Числові проміжки
2.2. Переріз і об'єднання числових проміжків
3.Властивості числових нерівностей і методичні особливості їх вивчення в шкільному курсі алгебри.
Методика вивчення числових нерівностей і їх властивостей у шкільному курсі математики
План
- Місце теми: «Числові нерівності» у програму. Основна мета вивчення, державні вимоги до рівня загальноосвітньої підготовки учнів.
-
Введення поняття числової нерівності.
- Числові проміжки
- Переріз і об'єднання числових проміжків
- Властивості числових нерівностей і методичні особливості їх вивчення в шкільному курсі алгебри.
1. Місце теми у програмі. Основна мета вивчення та вимоги до підготовки учнів.
Пропедевтика вивчення теми: «Числові нерівності» починається ще в початковій школі, коли учні вчаться порівнювати кількість предметів, тощо.
В 5 класі в темі 1: «Натуральні числа», після того як вивчають, що називається натуральними числами, числом нуль, координатним променем, учні порівнюють натуральні числа. В темі 2: «дробові числа» спочатку порівнюють звичайні дроби з однаковими знаменниками, а вже потім – десяткові дроби. А вже в 6 класі у темі 2: «Звичайні дроби» діти описують правила порівняння звичайних дробів та розв’язують вправи, що передбачають порівняння дробів. В цьому ж класі після вивчення теми 4 учні порівнюють раціональні числа.
Левова частка вивчення числових нерівностей припадає на 9 клас. За навчальною програмою 16 годин присвячено вивченню теми 1: «Нерівності». В даній темі 8 годин відведено на вивчення числових нерівностей, їх властивостей та дій над ними.
Орієнтовне календарне планування
на тему: «Числові нерівності та їх властивості»
|
№ уроку |
Дата прове- дення |
Тема уроку |
Тип уроку |
Мета уроку |
При мітки |
|
Тема 1. НЕРІВНОСТІ (16 год) |
|||||
|
Тема 1.1 Числові нерівності та їх властивості (8 год) |
|||||
|
1 |
|
Числові нерівності. Доведення числових нерівностей |
Засвоєння знань, вироблення вмінь |
Домогтися засвоєння учнями змісту поняття числові нерівності, означення, що виражає залежність між співвідношеннями >, <, = і знаком різниці лівої та правої частин нерівності, а також виробити вміння доводити нерівності з використанням цього означення. |
|
|
2 |
|
Числові нерівності. Доведення числових нерівностей |
Закріплення знань, вироблення вмінь |
Домогтися засвоєння учнями змісту: додаткових нерівностей для суми взаємно обернених додатних чисел та середнього арифметичного двох невід’ємних чисел (у порівнянні з їх середнім геометричним) та доведення цих нерівностей; способу застосування доведених нерівностей при доведенні інших числових нерівностей. |
|
|
3 |
|
Основні властивості числових нерівностей. |
Засвоєння знань, вироблення первинних вмінь. |
Домогтися засвоєння учнями змісту основних властивостей числових нерівностей та їхніх наслідків, а також способу доведення цих властивостей. Виробити вміння застосовувати набуті знання при розв’язуванні вправ на порівняння буквених виразів та на доведення відповідних нерівностей. |
|
|
4 |
|
Основні властивості числових нерівностей. |
Доповнення знань, вироблення вмінь, відпрацювання навичок. |
Домогтися засвоєння учнями змісту поняття «оцінити значення виразу»; закріпити знання учнів про зміст властивостей числових нерівностей та їхніх наслідків. |
|
|
5 |
|
Почленне додавання і множення нерівностей. Застосування властивостей числових нерівностей для оцінювання значення виразу. |
Засвоєння знань, вироблення первинних умінь. |
Домогтися засвоєння учнями змісту поняття «додати нерівності почленно» та «перемножити нерівності почленно», а також продовжити роботу з відпрацюванням навичок доведення нерівностей, порівняння виразів із використанням означення та властивостей числових нерівностей. |
|
|
6 |
|
Почленне додавання і множення нерівностей. Застосування властивостей числових нерівностей для оцінювання значення виразу. |
Закріплення знань, вироблення вмінь. |
Домогтися закріплення учнями змісту: властивостей числових нерівностей і теорем про по членне додавання та множення нерівностей; наслідків іх властивостей числових нерівностей. Відпрацювати навички застосовувати набуті знання для розв’язування вправ. |
|
|
7 |
|
Розв’язування вправ. Підсумковий урок. |
Систематизація й узагальнення знань та вмінь. |
Повторити, систематизувати та узагальнити знання за розділом «Числові нерівності та їх властивості». |
|
|
8 |
|
Тематична контрольна робота |
Контроль знань та вмінь. |
Перевірити рівень знань та вмінь учнів, набутих ними під час вивчення розділу «Числові нерівності та їх властивості». |
|
Програма для класів з поглибленим вивченням математики передбачає вивчення теми «Нерівності» у 8 класі. Такий підхід дозволяє під час вивчення тем «Властивості квадратного кореня», «Розв’язування рівнянь з модулем», «Побудова графіків функцій» звернути увагу учнів на необхідність постійно мати на увазі множину допустимих значень виразів, які входять до рівнянь, а також відслідковувати перетворення, які можуть вплинути на множину допустимих значень змінних (розширити чи звузити її) у ході розв’язування рівнянь. Зазначене дозволяє суттєво урізноманітнити зміст завдань. На відміну від загальноосвітніх класів, вивчення теми «Нерівності» багато в чому спирається на апарат теорії множин, вивченийу відповідній темі, зокрема, запис розв’язків має виконуватися з використанням символіки теорії множин.
Друга тема курсу алгебри у 9–му класі «Доведення нерівностей» є продовженням і розширенням відповідної теми 8 класу. Проте у 8 класі на меті було набуття навичок розв’язувати нерівності, а в 9 класі – їх доведення. Треба розглянути кілька основних методів доведення нерівностей. Робота над цією темою формує в учнів евристичне мислення, навички аналізу і математичну інтуїцію.
8 клас Алгебра
|
К-ть год |
Зміст навчального матеріалу |
Державні вимоги до рівня загальноосвітньої підготовки учнів |
|
20 |
Тема 4. Нерівності Числові нерівності та їх властивості. Числові проміжки. Об’єднання та переріз числових проміжків. Нерівності з однією змінною. Розв’язування лінійних нерівностей з однією змінною. Рівносильні нерівності. Нерівність – наслідок до неї. Системи і сукупності лінійних нерівностей з однією змінною. Розв’язування лінійних нерівностей з параметром. Розв’язування рівнянь і нерівностей з модулем. |
Описує поняття: числова нерівність, нерівність із змінною. Формулює означення понять: розв’язок нерівності з однією змінною, рівносильні нерівності, нерівність – наслідок даної, розв’язок системи і сукупності кількох нерівностей з однією змінною. Доводить властивості числових нерівностей. Зображує на числовій прямій множини, задані за допомогою нерівностей. Розв’язує лінійні нерівності, а також системи і сукупності лінійних нерівностей з однією змінною. |
9 клас Алгебра
|
К-ть год |
Зміст навчального матеріалу |
Державні вимоги до рівня загальноосвітньої підготовки учнів |
|
15 |
Тема 2. Доведення нерівностей Основні методи доведення нерівностей. Нерівність Коші для двох чисел та їх застосування. Нерівності між середніми величинами двох додатних чисел (середнє гармонічне, середнє геометричне, середнє арифметичне, середнє квадратичне). [Нерівність Коші-Буняковського.] Метод використання відомих нерівностей. |
Описує основні методи доведення нерівностей: використання означення нерівності, доведення від супротивного, використання відомої нерівності. Доводить нерівність Коші для двох невід’ємних чисел, нерівність для суми двох додатних взаємно обернених чисел. Розв’язує вправи, у яких передбачено використання основних методів доведення нерівностей. |
2. Введення поняття числової нерівності
Щодо тлумачення числової нерівності можливі різні підходи. Тривалий час в шкільних підручниках обмежувались геометричним тлумаченням числової нерівності: число а називається більшим за число b, якщо точка, що зображує число а на координатній прямій, міститься праворуч від точки, що зображує число b.
Для будь-яких різних дійсних чисел а та b можна визначити, яке зних більше, а яке менше.
Говорять, що число а більше за число b, і записують а > b, якщо різниця а –b – додатне число; якщо ж різниця а –b – від’ємне число, то говорять, що число а менше від числа b, і записують а < b. Відповідно до цього означення будь-яке додатне число більше від нуля, будь-яке від’ємне число менше від нуля и менше довільного додатного числа. Для довільно заданих чисел а і b справедливе одне і тільки одне з відношень: а > b, а < b, а = b.
Знаки >, < називаються знаками строгих нерівностей. Іноді використовують знаки ≥, ≤ - знаки нестрогих нерівностей; запис а≤b означає, що справедливе одне з двох: або число а менше числа b, або число а дорівнює числу b. Наприклад, 3 ≤ 5, 5 ≥ 5 – справедливі нерівності. Нерівності а > b та с > d називаються нерівностями одного знаку; нерівності а > b та с < d називаються нерівностями протилежних знаків. Якщо числа а, b, с такі, що а < b та b < с , то використовують запис а < b < с (подвійна нерівність). Подвійну нерівність а < b < с записують також як систему нерівностей ![]() . Система нерівностей
. Система нерівностей ![]() правильна, якщо правильні обидві її нерівності. Більш загально система нерівностей
правильна, якщо правильні обидві її нерівності. Більш загально система нерівностей
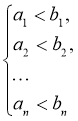
є правильною тоді і тільки тоді, коли правильні всі її нерівності. Так, система
![]()
Неправильна, бо містить неправильну нерівність 0>2. аналогічний зміст має система, що містить нестрогі нерівності.
Крім наведених вище знаків нерівності (≥, ≤ , <, >) часто використовують ще знак ≠ (не дорівнює). Якщо, наприклад, співвідношення «не більше» (а≤b) означає а < b або а = b, то співвідношення «не дорівнює» (а≠b) означає а < b або а > b.
Відношення «не дорівнює» принципово відрізняється від «не більше». Для всіх відношень рівності і нерівності, які позначаються знаками =, <, >, ≥, ≤, справджується властивість транзитивності, тобто із а ≤ b і b ≤ с випливає, що а ≤ с . А для відношення «не дорівнює» така властивість може не справджуватись: із а ≠b і b ≠ с не завжди випливає а ≠ с. Наприклад, 2 ≠ 3 і 3 ≠ 2, але відношення 2 ≠ 2 хибне, неправильне. Тому далі, говорячи про нерівності, матимемо на увазі два числа, або вирази, сполучені будь-яким із знаків <, >, ≥, ≤, але не знаком ≠.
Приклад 1
Доведіть, що при будь-яких значеннях а є правильною нерівність
(а + 1) (а + 2) > а (а + 3).
Розв'язання
Для розв'язання достатньо показати, що при будь-якому значенні а різниця лівої і правої частин даної нерівності є додатною. Маємо:
(а + 1) (а + 2) - а (а + 3) = а2 + 2а + а + 2 - а2 - 3а = 2. У таких випадках говорять, що доведено нерівність (а + 1) (а + 2) > а (а + 3).
Приклад 2
Доведіть нерівність (а - 3)2 < 2а2 - 6а + 10, де а — будь-яке дійсне число.
Розв'язання
Розглянемо різницю лівої і правої частин даної нерівності:
(а - 3)2 - (2а2 - 6а + 10) = а2 - 6а + 9 - 2а2 + 6а - 10 = -а2 - 1 = -а2 + (-1).
При будь-якому значенні а маємо, що -а2 ≤ 0. Сума не додатного і від'ємного чисел є число від'ємне. Отже, -а2 + (-1) < 0. Звідси випливає, що (а-3)2 < 2а2 - 6а + 10 при будь-якому значенні а.
Приклад 3
Доведіть нерівність ![]() , де а > 0, b > 0.
, де а > 0, b > 0.
Розв'язання
Розглянемо різницю лівої і правої частин даної нерівності. Маємо:
![]()
![]()
Вираз ![]() набуває невід'ємних значень при будь-яких невід'ємних значеннях змінних а і b. Отже, нерівність, що доводиться, є правильною.
набуває невід'ємних значень при будь-яких невід'ємних значеннях змінних а і b. Отже, нерівність, що доводиться, є правильною.
Зауважимо, що вираз ![]() називають середнім геометричним чисел а і b.
називають середнім геометричним чисел а і b.
Приклад 4
Доведіть, що а2 - аb + b2 > 0 при будь-яких значеннях а і b.
Розв'язання.
Маємо:
![]()
Оскільки ![]() і
і ![]() при будь-яких значеннях а і b, то
при будь-яких значеннях а і b, то ![]() при будь-яких значеннях а і b. Отже, а2 - а b + b2 > 0 при будь-яких значеннях а і b.
при будь-яких значеннях а і b. Отже, а2 - а b + b2 > 0 при будь-яких значеннях а і b.
Приклад 5
Яка з різниць більша і в скільки разів:
20092010 - 20092009 чи 20092009 - 20092008 ?
Розв’язання
20092010 – 20092009 = 20092009 (2009-1) = 2008∙20092009;
20092009 – 20092008 = 20092008 (2009-1) = 2008·20092008;
(2008·20092009) : (2008·20092008) = 2009.
Відповідь. Перша різниця більша від другої в 2009 разів.
2.1 Числові проміжки
Візьмемо два числа а і b, такі, що а < b, та відмітимо на координатній прямій відповідні точки.
Довільна точка х, що лежить між а і b, відповідає числу, що задовольняє нерівностям а < х < b. Множину всіх чисел х, що задовольняють ці нерівності, позначають (а; b) і називають інтервалом.
Множину всіх чисел х, кожне з яких задовольняє нерівності а ≤ х ≤ b, позначають [а; b] і називають відрізком.
Інтервал і відрізок – це скінченні числові проміжки. Скінченні числові проміжки бувають ще двох видів: [а; b) – це множина чисел х, що задовольняють нерівності а ≤ х < b , та (а; b] - це множина чисел х, що задовольняють нерівностям а < х ≤ b. Ці проміжки називаються півінтервалами.
Існують і нескінченні числові проміжки. Множину всіх чисел х, що задовольняють нерівність х ≥ а, позначають [а; +∞) і називають променем., а множину всіх чисел х, що задовольняють нерівність х > а, позначають (а; +∞) и називають відкритим променем.
Аналогічним може бути промінь виду (-∞; b] (числа, що задовольняють нерівність х ≤ b) і відкритий промінь виду (-∞; b) (числа, що задовольняють нерівність х < b).
В наведеній нижче таблиці для кожного виду числового проміжку подані його геометричні зображення, позначення та запис за допомогою нерівності.
|
Вид проміжку |
Геометричне Зображення |
Позначення |
Запис за допомогою Нерівності |
|
Інтервал |
|
(а; b) |
а < х < b |
|
Відрізок |
|
[а; b] |
а ≤ х ≤ b |
|
Півінтервал |
|
(а; b] |
а < х ≤ b |
|
Пів інтервал |
|
[а; b) |
а ≤ х < b |
|
Промінь |
|
[а; +∞) |
х ≥ а |
|
Промінь |
|
(-∞; b] |
х ≤ b |
|
Відкритий Промінь |
|
(а; +∞) |
х > а |
|
Відкритий промінь |
|
(-∞; b) |
х < b |
2.2.Переріз і об'єднання числових проміжків
|
Означення |
Приклади |
|
Перерізом двох числових проміжків називають їх спільну частину. Переріз проміжків позначається ∩. Перерізом числових проміжків є:
|
[-1;5]∩(3;9]=(3;5]
(-5;-2]∩[-2;9)={-2}
(-1;0]∩[1;5)=Ø
|
|
Об'єднанням двох числових проміжків називають множину чисел, яка містить кожне число кожного проміжку і тільки такі числа. Об'єднання проміжків позначається U. Об'єднанням числових проміжків є:
|
[-1;5]U(3;9]=[-1;9]
(-1;0]U[1;5)
|
3. Властивості числових нерівностей і методичні особливості їх вивчення в шкільному курсі алгебри.
Нагадавши учням, як порівнювати натуральні, цілі та інші числа, та після того як було вивчено означення числової нерівності, їх різні види, розв’язано ряд вправ тощо, далі дев’ятикласники вивчають властивості числових нерівностей. А також деякі з основних властивостей доводяться (одні доведені в підручнику, а інші вчитель може запропонувати довести учням самостійно, або зробити це разом на уроці).
При розгляданні властивостей нерівностей зручно використовувати символ слідування → та рівносильності ↔.
Запис а > b → с > d означає, що якщо правильна нерівність а > b, то правильна нерівність с > d, тобто нерівність с > d випливає з нерівності а > b, або нерівність с > d є наслідком нерівності а > b.
Запис а > b ↔ с > d означає, що справедливі два твердження: а>b → с>d та с > d → а > b, тобто нерівності а > b та с > d рівносильні. Наприклад, а > b ↔ а - b > 0 за означенням.
Аналогічний зміст мають символи → та ↔ у випадку нестрогих нерівностей або їх систем. Наприклад,
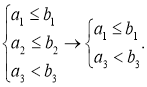
Можна розглядати ланцюг нерівностей.
Якщо а1 > b1 → а2 > b2 → . . . → аn > bn, то а1 > b1 → аn > bn.
Якщо а1 > b1 ↔ а2 > b2 ↔ . . . ↔ аn > bn, то а1 > b1 ↔ аn > bn.
Аналогічно можна розглядати ланцюги систем нерівностей.
Автори різних підручників пропонують різні підходи щодо вивчення основних властивостей числових нерівностей. Так наприклад, у підручнику Алгебра 9кл. (Г.П. Бевз, В.Г. Бевз) – [1] автори пропонують: спочатку у §2 доводиться п’ять теорем-властивостей, а потім у §3 «Подвійні нерівності» наведені теореми – дії над подвійними нерівностями. У підручнику [2] – Алгебра 9кл. (А.Г. Мерзляк, В.Б. Полянський, М.С. Якір) в §2 доведено три теореми-властивості та два наслідки до них, а також виділено правила дій над числовими нерівностями. В §3 «Додавання і множення числових нерівностей. Оцінювання значення виразу» дві теореми (слід також зауважити, що автори дають пояснення, що означає та чи інша теорема), перед початком вивчення нової теми міститься теоретичний матеріал з прикладами на тему «Про деякі способи доведення нерівностей». Проаналізувавши і інші підручники, можна зробити висновок, що подання теоретичного матеріалу дещо відрізняється, але після вивчення теми та розв’язання ряду завдань можна прийти до одного результату – виробити в учнів знання та вміння щодо розв’язування та доведення числових нерівностей, а також розвинути в учнів більш широке логічне мислення.
Вивчаючи властивості числових нерівностей, доцільно скористатися таблицею (таблицю наведено нижче), в якій зіставляють відношення «рівне», «більше», «менше» на множині чисел. З таблиці випливає спільне в означенні та властивостях числових рівностей і числових нерівностей, виявляються відмінності цих відношень, що сприятиме кращому запам'ятовуванню їх.
Таблиця . Порівняння властивостей числових рівностей і нерівностей
|
Числові рівності |
Числові нерівності |
|
Число а називають таким, що дорівнює числу b, якщо різниця а - b дорівнює нулю
За будь-яких а і b, якщо а=b, то b = а. За будь-яких а, b і с, якщо а = b і b = с, то а = с (властивість транзитивності рівностей) Якщо а = b і с — будь-яке число, то а + с = b + с Якщо а = b і с - будь-яке число, то а с = b с. Якщо а = b і с = d, то а + с = b + d . Якщо а = b і с = d, то а с = b d Наслідок. Якщо а = b, то а2= b2
Якщо а = b і а ≠0, b ≠ 0, то
|
Число а називають більшим за число b, якщо різниця а - b є додатним числом. Число а називають меншим від числа b, якщо різниця а - b є від'ємним числом За будь-яких а і b, якщо а < b, то b > а і, навпаки, якщо а > b , то b < а За будь-яких а, b і с, якщо а < b і b < с, то а < с; якщо а > b і b > с, то а > с (властивість транзитивності нерівностей) Якщо а < b і с — будь-яке число, то а + с < b + с Якщо а < b і с > 0, то ас < bс; якщо а < b і с < 0, то ас > bс; якщо а > b і с > о, то ас > bс; якщо а > b і с < о, то ас < bс Якщо а < b і с < d, то а + с < b + d; якщо а > b і с > d, то а + с > b + d Якщо а < b і с < d (а, b, с, d — додатні числа), то ас < b d Наслідок. Якщо а < b, а > 0, b > 0, то а2< b 2 Якщо а < b (а і b — числа одного знака), то
|
Основні властивості числових нерівностей.
Теорема1. Якщо а > b і b > с, то а > с.
Доведення. Оскільки за умовою а > b і b > с, то різниці а - b і b - с є додатними числами. Тоді додатною буде їх сума (а - b) + (b - с). Маємо: (а - b) + (b - с) = а - с. Отже, різниця а - с є додатним числом, а тому а > с. Теорему доведено.
Аналогічно доводиться властивість: якщо а < b і b < с, то а < с.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Теорему 1 можна проілюструвати геометрично: якщо на координатній прямій точка А (а) лежить праворуч від точки В (b), а точка В (b) — праворуч від точки С (с), то точка А (а) лежить праворуч від точки С (с) (рис.1).
Теорему 1 можна проілюструвати геометрично: якщо на координатній прямій точка А (а) лежить праворуч від точки В (b), а точка В (b) — праворуч від точки С (с), то точка А (а) лежить праворуч від точки С (с) (рис.1).
Теорема 2. Якщо а > b і с — будь-яке число, то а + с > b + с.
Доведення. Розглянемо різницю (а + с) - (b + с). Маємо: (а + с) - (b + с) = а - b. Оскільки за умовою а > b, то різниця а - b є додатним числом. Отже, а + с > b + с. Теорему доведено.
Аналогічно доводять властивість: якщо а < b і с — будь-яке число, то а + с < b + с.
Оскільки дію віднімання можна замінити дією додавання (а - с = а + (-с)), то, ураховуючи теорему 2, можна зробити такий висновок.
Якщо до обох частин правильної нерівності додати або від обох частин правильної нерівності відняти одне й те саме число, то отримаємо правильну нерівність.
Наслідок. Якщо будь-який доданок перенести з однієї частини правильної нерівності в другу, замінивши знак доданка па протилежний, то отримаємо правильну нерівність.
Доведення. Нехай нерівність а > b + c є правильною. Віднімемо від обох її частин число с. Отримаємо: а - с > b + с - с, тобто а - с > b. Наслідок доведено.
Теорема 3. Якщо а > b і с — додатне число, то ас > bс. Якщо а > b і с — від'ємне число, то ас < bс.
Доведення. Розглянемо різницю ас - bс. Маємо: ас - bс = с(а- b).
За умовою а > b, отже, різниця а - b є додатним числом.
Якщо с > 0, то добуток с (а - b) додатний, а отже, різниця ас - bс є додатною, тобто ас > bс.
Якщо с < 0, то добуток с (а - b) від'ємний, а отже, різниця ас - bс є від'ємною, тобто ас < bс. Теорему доведено.
Аналогічно доводять властивість: якщо а < b і с — додатне число, то ас < bс; якщо а < b і с — від'ємне число, то ас > bс.
Оскільки дію ділення можна замінити дією множення ![]() , то, ураховуючи теорему 3, можна зробити такий висновок.
, то, ураховуючи теорему 3, можна зробити такий висновок.
Якщо обидві частини правильної нерівності помножити або поділити на одне й те саме додатне число, то отримаємо правильну нерівність.
Якщо обидві частини правильної нерівності помножити або поділити на одне й те саме від'ємне число і поміняти знак нерівності на протилежний, то отримаємо правильну нерівність.
Наслідок. Якщо а b > 0 і а > b, то![]() .
.
Доведення. Поділимо обидві частини нерівності а > b на додатне число ab. Отримаємо правильну нерівність ![]() , тобто
, тобто ![]() . Звідси
. Звідси ![]() . Наслідок доведено.
. Наслідок доведено.
Звернемо увагу: вимога, щоб числа а і b були однакового знака (аb > 0), є суттєвою. Справді, нерівність 5 > -3 є правильною, проте нерівність ![]() є неправильною.
є неправильною.
Приклад. Відомо, що -4 ≤ а ≤ -2. Доведіть, що
![]()
Розв’язання.
Маємо: -4 ≤ а ≤ -2. Тоді за теоремою 3 отримуємо -12 ≤ 3а ≤ -6. Застосовуючи теорему 2, одержимо -7 ≤ 3а-5 ≤ -1. Користуючись наслідком з теореми 3, можна записати, що ![]() , тобто
, тобто ![]() . Звідси
. Звідси ![]() .
.
Розглянемо приклади.
- Якщо з першого поля зібрали не менше ніж 40 т жита, а з другого поля — не менше ніж 45 т, то очевидно, що з двох полів разом зібрали не менше ніж 85 т жита.
- Якщо довжина прямокутника не більша за 70 см, а ширина — не більша за 40 см, то очевидно, що його площа не більша за 2800 см2.
Висновки з цих прикладів є інтуїтивно очевидними. Справедливість їх підтверджують такі теореми.
Теорема 4. (про почленне додавання нерівностей). Якщо а > b і с > d, то а + с> b + d.
Доведення. Розглянемо різницю (а + с) - (b + d). Маємо:
(а + с) - (b + d) = а + с - b - d = (а - b) + (с - d).
Оскільки a> b і с > d, то різниці a-b i c-dє додатними числами. Отже, різниця, що розглядається, є додатною, тобто a + c>b+ d. Теорему доведено.
Аналогічно доводиться властивість: якщо а < b і с < d, то а + с < b + d.
Теорема 4 означає, що при почленному додаванні правильних нерівностей однакового знака результатом є правильна нерівність того самого знака.
Зазначимо, що теорема 4 справедлива й у випадку почленного додавання трьох і більше нерівностей. Наприклад, якщо а1 > b1, а2 > b2 і а3 > b3, то а1 + а2 + а3 > b1 + b2 + b3.
Теорема 5 (про почленне множення нерівностей). Якщо а > b, с > d і а, b, с, d — додатні числа, то ас > bd.
Доведення. Розглянемо різницю ас - bd. Маємо:
ас - bd = ас - bс + bс - bd = с (а - b) + b (c - d).
За умовою а - b > 0, с - d> 0, с> 0, b > 0. Отже, різниця, що розглядається, є додатною. З цього випливає, що ас > bd. Теорему доведено.
Аналогічно доводиться властивість: якщо а < b, с < d і а, b, с, d — додатні числа, то ас < bd.
Теорема 5 означає, що при почленному множенні правильних нерівностей однакового знака, у яких ліві та праві частини — додатні числа, результатом є правильна нерівність того самого знака.
Звернемо увагу: вимога, щоб обидві частини нерівностей, які множать, були додатними, є суттєвою. Справді, розглянемо дві правильні нерівності -2 > -3 і 4 > 1. Помноживши почленно ці нерівності, отримуємо нерівність -8 > -3, яка не є правильною.
Зауважимо, що теорема залишається справедливою і у випадку почленного множення трьох і більше нерівностей. Наприклад, якщо a1, а2, а3, b1, b2, b3 — додатні числа, причому а1 > b1, а2 > b2, а3 > b3, то а1 а2 а3 > b1 b2 b3.
Наслідок. Якщо а > b і а, b — додатні числа, то ал > bп, де п — натуральне число.
Доведення. Запишемо п правильних нерівностей а > b:
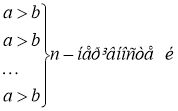
Оскільки а і b — додатні числа, то можемо помножити почленно п записаних нерівностей. Отримаємо аn > bn. Наслідок доведено.
Зазначимо, що всі розглянуті властивості нерівностей є справедливими і в тому випадку, коли нерівності є нестрогими:
якщо а ≥ b і с ≥ d, то а + с ≥ b + d;
якщо a ≥ b,c ≥ d i a,b,c,d — додатні числа, то ас ≥ bd;
якщо а ≥ b і а, b — додатні числа, то ап ≥ bп, де п — натуральне число.
Автори підручника Алгебра 9 Бевз Г.П. та Бевз В.Г. виділяють окремо параграф для вивчення подвійних нерівностей і пропонують учням наступні теореми.
Теорема 6. Якщо до кожної частини правильної подвійної нерівності додати одне й те саме число, то одержимо правильну подвійну нерівність.
Доведення. Якщо а < х < b, то правильні нерівності а < х і х < b. Тоді згідно з теоремою 2 для будь-якого дійсного числа с правильні нерівності а + с < х+ с і х+ с< b+ с. Отже, а+ с< х+ с< b+ с. Теорему доведено.
Число с може бути як додатним, так і від'ємним. Наприклад: якщо 2,5 < х – 3 < 2,6 і с = 3, то 5,5 < х < 5,6; якщо 0,7 < х + 1< 1,2 і с = -1, то -0,3 < х < 0,2. Подібним способом можна довести такі твердження:
- якщо а < х < b і k > 0, то ka < kx < kb;
- якщо а < х < b і k < 0, то kb < kx < ka;
- якщо а < х < b і с < у < d, то:
a + c < x + y < b + d;
а - d < х - у < b - с;
ас < ху < bd (при а > 0 і с > 0);
![]()
Введення поняття «оцінити» автори різних підручників пропонують аналогічні, так наприклад у підручнику [2] вони пропонують зробити це так:
Часто значення величин, які є результатом вимірювань, не є точними. Вимірювальні прилади, як правило, дозволяють лише встановити межі, між якими знаходиться точне значення.
Нехай, наприклад, у результаті вимірювання ширини х і довжини у прямокутника було встановлено, що 2,5 см < х < 2,7 см і 4,1 см < у < 4,3 см. Тоді за допомогою теореми 4 можна оцінити площу прямокутника. Маємо:
2,5 см < х < 2,7 см
х 4,1 см < у < 4,3 см
![]() 10,25 см2 < ху < 11,61 см2
10,25 см2 < ху < 11,61 см2
Узагалі, якщо відомо значення меж величин, то, використовуючи властивості числових нерівностей, можна знайти межі, тобто оцінити значення виразу, який містить ці величини.
Приклад Дано: 6< а <8і10<b<12. Оцініть значення виразу:
1) а + b; 2) а - b; 3) ab; 4) ![]() ; 5) 3a - 1/2b.
; 5) 3a - 1/2b.
Розв'язання
1) Застосувавши теорему про почленне додавання нерівностей,
отримуємо:
6 < а < 8
+ 10 < b < 12
16 < а + b < 20
2) Помноживши кожну частину нерівності 10 < b < 12 на -1,
отримуємо -10 > -b > -12 або -12 < -b < -10. Ураховуючи,
що а - b = а + (-b), далі маємо:
6 < a < 8
+ -12 < -b < -10
-6 < a - b < -2
3) Оскільки a > 6 і b > 10, то a і & набувають додатних значень. Застосувавши теорему про почленне множення нерівностей, отримуємо:
6 < а < 8
х 10 < b < 12
![]() 60< аb < 96
60< аb < 96
4) Оскільки 10 < b < 12, то ![]() Ураховуючи, що
Ураховуючи, що ![]() , маємо:
, маємо:
6 < а < 8
![]() х
х ![]()
1/2< ![]() < 4/5
< 4/5
5) Помножимо кожну частину нерівності 6< а <8 на 3,а кожну частину нерівності 10 < b < 12 на 1/2:
![]()
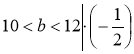
![]()
![]()
![]()
Додамо отримані нерівності:
![]()
![]()
![]()
![]()
Відповідь: 1) 16 < а + b < 20; 2) -6 < а - b < -2; 3) 60 < а b < 96;
4) 1/2< ![]() < 4/5; 5)
< 4/5; 5) ![]()


про публікацію авторської розробки
Додати розробку









