Міні-підручник "Множення векторів"

Про матеріал

Тренувально-узагальнюючий збірник завдань з геометрії "Множення векторів" для здобувачів освіти 9 класу.

Перегляд файлу

$C:\Users\Саня\Desktop\міні-підручник\IMG_0001.jpg$

Емблема гимназии

Гімназія № 107 «Введенська»

Кафедра математики

Тренувально-узагальнюючий

збірник завдань

з геометрії

учня (учениці) 9 - __ класу

_________________________________

$G:\1\20110418_vectorsvg_.png$

Київ – 2020

Алгебра – це не лише писана геометрія,

а геометрія – зображена алгебра

С. Жермен

План вивчення теми:

І частина

Властивості векторів.
Множення вектора на число.
Колінеарні вектори.

ІІ частина

Скалярний добуток векторів:

Означення скалярного добутку;
Властивості скалярного множення;
Скалярний добуток векторів, заданий своїми координатами.

$G:\1\image_preview.jpg$

І частина

Властивості векторів

$C:\Users\Саня\Desktop\міні-підручник\IMG_0003.jpg$

Множення вектора на число

Добутком вектора на дійсне число λ називається вектор , колінеарний вектору , причому:

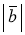= |λ| · ;
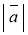якщо λ > 0, то вектор 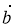однаково напрямлений з вектором ;
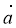якщо λ < 0, то вектор 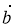протилежно напрямлений вектору .

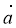Властивості добутку вектора на число

(λ₁λ₂) 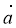= λ₁(λ₂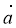) (сполучний закон);
λ₁ 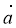+ λ₂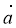 = (λ₁ + λ₂) 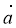(розподільний закон);
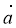λ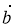 + λ = λ(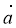 + 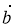) (розподільний закон);
0 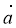· = λ · = .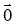

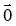Координати вектора

Координати вектора λ дорівнюють добутку числа λ на відповідні координати вектора . Якщо вектори задано на площині, то λ(а₁; а₂) = (λа₁; λа₂).

Колінеарні вектори

Два ненульові вектори та колінеарні тоді та тільки тоді, коли = λ, λ — відмінне від нуля число.

Теорема. Якщо вектор має координати (a₁; a₂), то вектор λ має координати (λа₁; λа₂).

Наслідок. Якщо вектори колінеарні, то їхні відповідні координати пропорційні, тобто якщо вектори (a₁; a₂) і

(b₁; b₂) колінеарні, то .

Обернене твердження. І навпаки, якщо відповідні координати двох векторів пропорційні, то ці вектори колінеарні, тобто якщо і (a₁; a₂), (b₁; b₂), то вектори і колінеарні.

Приклад 1

Серед векторів (-2; 4), (2; 2), (0; -1), (1; -2) знайдіть колінеарні.

Розв'язання:

Оскільки вектори колінеарні, якщо їхні відповідні координати пропорційні, то маємо = -2, звідси вектори i колінеарні.

Відповідь: i .

Приклад 2

Знайдіть довжину вектора (6; у), якщо він колінеарний вектору +, де (-2; 0), (0; 1).

Розв'язання:

Нехай +=, тоді (-2+0; 0+1)=(-2; 1). Оскільки вектори

і колінеарні, то , звідси у = = -3, тоді (6; -3) і

= = = = = 3.

Відповідь: 3

Завдання № 1.1

Побудуйте вектор , довжина якого дорівнює 4 см. Побудуйте за допомогою лінійки вектори:

а) 2; б) -2; в) ; г) -.

Завдання № 1.2

Дано (1; -3), (-2; 1). Знайдіть координати вектора:

а) 2; б) -3; в) 2 + 3; г) 2 – 3.

Розв'язання:

_____________________________________________________________________________

Відповідь:________________________________________

Завдання № 1.3

Дано вектори (3; 2) і (0; -1). Знайдіть вектор

= -2 + 4 та його абсолютну величину.

Розв'язання:

____________________________________________________________________________________

Відповідь:____________________________________________

Завдання № 1.4

Дано вектори: (3; 0); (7; 4). Запишіть:

а) координати вектора + ;

_____________________________________________________________________________

б) координати вектора – ;

_____________________________________________________________________________

в) координати вектора – ;

_____________________________________________________________________________

г) довжину вектора – ;

_____________________________________________________________________________

д) координати вектора 2 – ;

_____________________________________________________________________________

є) довжину вектора 2 – ;

_____________________________________________________________________________

Завдання № 1.5

При якому значенні m вектори (15; m) і (18; 12) колінеарні?

Розв'язання:

____________________________________________________________________________________

Відповідь:____________________________________________

Завдання № 1.6

Чи колінеарні вектори і , якщо А(3; -2), B(-1; 4), C(1; 3), D(-3; 9)?

Розв'язання:

____________________________________________________________________________________

Відповідь:____________________________________________

Завдання № 1.7

При якому значенні n вектори і колінеарні, якщо А(1; 0), В(3; п), С(2; 2), D(5; 4)?

Розв'язання:

____________________________________________________________________________________

Відповідь:____________________________________________

ІІ частина

$C:\Users\Саня\Desktop\кут між векторами.jpg$ Скалярний добуток векторів

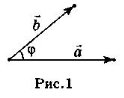
Скалярним добутком векторів і називається добуток довжин цих векторів на косинус кута між ними, тобто

· = || · || cosφ (рис. 1).

Позначення: (·), або , або (; ).

Два ненульові вектори тоді і тільки тоді взаємно перпендикулярні, коли їх скалярний добуток дорівнює нулю, тобто · = 0 ( , ).

Властивості скалярного добутку

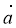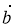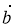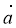·= · (переставний закон);
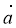² = |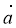|², або || = = ;
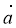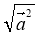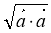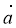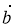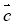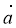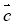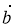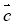( + ) · = · + · (розподільний закон);
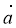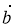(λ) · = λ(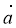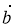·) (сполучний закон відносно скалярного множника).

Примітка 1. Косинус кута між ненульовим векторами та виражається формулою 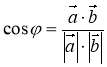, яка випливає з означення скалярного добутку.

Примітка 2. Властивість 2 скалярного добутку, а саме формула || = = , дозволяє обчислювати довжину вектора в загальному випадку.

Примітка 3. Розподільний закон справджується для будь-якого скінченного числа доданків. Наприклад, правильна формула ( + + ) · = · + · + ·.

Скалярний добуток двох векторів, які задано координатами

Скалярний добуток двох векторів, які задано координатами, дорівнює сумі добутків відповідних координат. Якщо задано вектори (a₁; a₂) і (b₁; b₂) на площині, то .

Наслідки:

Наслідок 1. Умова перпендикулярності двох векторів, які задано координатами

тобто якщо , то .

Наслідок 2. Формула довжини вектора :

Наслідок 3. Формула для обчислення кута між векторами (a₁; a₂) і (b₁; b₂):

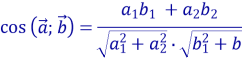
Приклад 1.

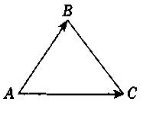
$C:\Users\Саня\Desktop\Безымянный.jpg$

Сторона рівностороннього трикутника ABC дорівнює 13. Знайдіть скалярний добуток .

Розв'язання:

Оскільки , A = 60°, то

Відповідь. 84,5.

Приклад 2.

Задано вектори = – 4, = 3 + 2, які взаємно перпендикулярні. Вектори і — одиничні вектори. Знайдіть кут між векторами і (в градусах).

Розв'язання:

Оскільки || = = 1 і · = 0, то маємо

· = ( – 4)(3 + 2) = 3²+ 2 – 12 – 8² =

=3 · ||² – 10|||| соsφ – 8||² = 31 - 1011cosφ – 81 =

= –5 – 10cosφ,

тоді –5 – 10cosφ = 0, соsφ = –, φ = 120°.

Відповідь. 120°.

Завдання № 2.1

Знайдіть кут між векторами (1; 2) і .

Розв'язання:

____________________________________________________________________________________

Відповідь:____________________________________________

Завдання № 2.2

Доведіть, що вектори (т; п) і (-n; m) перпендикулярні або дорівнюють нулю.

Розв'язання:

____________________________________________________________________________________

Відповідь:____________________________________________

Завдання № 2.3

Дано вектори (3; 4) і (m; 2). При якому значенні т вони перпендикулярні?

Розв'язання:

____________________________________________________________________________________

Відповідь:____________________________________________

Завдання № 2.4

Дано вершини трикутника ABC: А, В,

С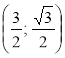. Знайдіть його кути.

Розв'язання:

Якщо початок вектора 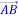є точка А(х_А; у_А), а кінець вектора — точка В(х_В; у_В), то 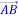(х_В – х_А; у_В – у_А).

____________________________________________________________________________________

Відповідь:____________________________________________

Завдання № 2.5

Дано вектори (1; 0) і (1; 1). Знайдіть таке число х, щоб вектор + x був перпендикулярний до вектора .

Розв'язання:

____________________________________________________________________________________

Відповідь:____________________________________________

Тренувально-узагальнюючий збірник завдань розроблено на кафедрі природничо-математичних дисциплін.

Автор-укладач Бережна Юлія Миколаївна – вчитель математики.

docx

Завантажити

Зберегти на потім

Додав(-ла)

Бережна Юлія Миколаївна

Пов’язані теми

Геометрія, 9 клас, Матеріали для друку

До підручника

Геометрія 9 клас (Бурда М.І., Тарасенкова Н.А.)

Додано

10 січня 2020

Переглядів

2950

Оцінка розробки

Відгуки відсутні