Урок з геометрії у 9-Б класі на тему: "Правильні многокутники. Довжина кола і площа круга"
Гімназія №9
Кіровоградської міської ради
Кіровоградської області
Урок з геометрії у 9-Б класі
на тему:
"Правильні многокутники. Довжина кола і площа круга"
Вчитель математики:
Івлєва Наталія Іванівна
Кропивницький 2019-2020
Тема: "Правильні многокутники. Довжина кола і площа круга"
Мета: систематизувати знання учнів з даної теми, формувати вміння застосовувати їх до розв`язування задач практичного змісту, розширити уявлення учнів про сферу застосування правильних многокутників, розвивати навички колективної роботи у поєднані з самостійною; вчити учнів висловлюватись мовою математики; розвивати логічне мислення, творчі здібності учнів; викликати інтерес до вивчення математики, виховувати наполегливість в досягнені мети.
Тип уроку: систематизація знань, умінь, навичок.
Обладнання: мультимедійний проектор, роздатковий матеріал
Хід уроку
- Організаційний момент
- Мотивація навчальної діяльності
Математика - це мова, на якій написана книга природи.
Галілео Галілей
Хочу розпочати урок словами італійського мислителя, фізика, астронома, математика та поета Галілео Галілея: «Математика - це мова, на якій написана книга природи». Він стверджував, що літерами даної мови є трикутники, кола, квадрати та інші математичні фігури, без допомоги яких людині неможливо пізнати навколишній світ, зрозуміти закони природи. Сьогодні на уроці ми в цьому впевнимося.
Тема нашого уроку: „ Правильні многокутники. Довжина кола і площа круга”. Ви вивчили основні поняття та формули з даної теми, розв’язали задачі. Тепер спробуємо застосувати ці знання до розвязування практичних задач. Але спочатку дещо пригадаємо.
- Актуалізація опорних знань
 3.1 Усно: Чи вірне твердження, вислів, означення ?
3.1 Усно: Чи вірне твердження, вислів, означення ?
https://learningapps.org/display?v=pafrcr8h219
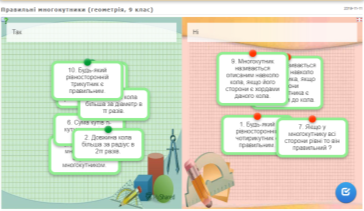
3.2 Повторюємо формули усно за картками
Які величини можна обчислити за наступними формулами?
Довжина кола
Площа круга
Внутрішній кут правильного многокутника
Довжина дуги кола
Площа кругового сектора
Радіус вписаного кола
Радіус описаного кола
Площа квадрата
Площа правильного трикутника,
Площа правильного шестикутника
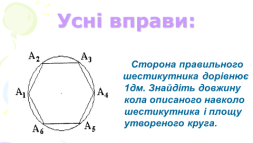
3.3 Усні вправи. (слайд 1-6)
Учні читають умову задачі на слайді, дають відповідь на неї усно. Після відповіді учнів на екрані з’являється розв’язок до цієї задачі.

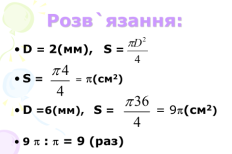
- Формування вмінь і навичок
4.1. Тренувальні вправи.
Учні розв’язують вправи самостійно і знаходячи відповідь у таблиці розгадують закодоване слово - природа. (слайд 7)
|
2,5 |
3 |
108 |
6 |
9 |
2 |
4 |
|
3 2 |
10 |
|
И |
Б |
П |
А |
О |
Р |
У |
Р |
Д |
Г |
- Обчислити внутрішній кут правильного 5 – кутника.
(L= ((n-2)/n)* 180 = 108)
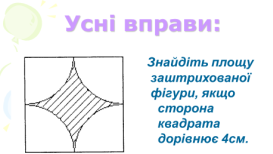
2. Обчислити радіус кола, вписаного в правильний чотирикутник із стороною
4см. ( r = 2)
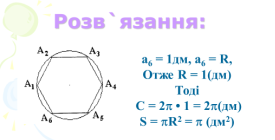
3.Знайти сторону правильного 6 – кутника, якщо радіус описаного кола навколо
нього – 2,5см. ( а6=R, а6 = 2* 2,5 sin30 = 2*2,5*1/2 = 2,5)
4. Радіус кола – 3см. Знайти довжину дуги, якщо ∠АОВ = 60°.
( L = ![]() , L =
, L = ![]() =
= ![]() (см))
(см)) 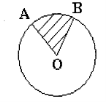
5. Знайти площу кільця, якщо радіус великого кола дорівнює 5 дм, а радіус малого кола – 4 дм. (Sкільця = Sв. кр. – Sм. кр. = 25![]() - 16
- 16![]() = 9
= 9![]() (дм2))
(дм2))

6. Радіус кола – 3см. Знайти площу сектора АОВ, якщо ∠АОВ = 60°.
(S=![]() , S =
, S = ![]() =
= ![]() (см2) )
(см2) ) 
7. Довжина дуги кола, радіус якого - 30см, дорівнює см. . Знайти градусну міру дуги. ( L = ![]() , =(*30*α)/180 , α= /( /6)=6°)
, =(*30*α)/180 , α= /( /6)=6°)
4.2 Індивідуальне завдання для 1 учня за ПК.
https://learningapps.org/display?v=phshhnppn19
4.3 Правильні многокутники в природі
Як пов’язані многокутники і природа? У природі часто зустрічаються різноманітні правильні багатокутники. Віртуозно компонуючи їх, природа створила безліч складних, дивно красивих, легких, міцних і економічних конструкцій. (слайд 12-13)

Один із прикладів - бджолині стільники, які являють собою багатокутник покритий правильними шестикутниками.


Чому бджоли вибрали саме шестикутник? Для відповіді на це питання потрібно порівняти периметри різних багатокутників, що мають однакову площу. Нехай дано правильний трикутник, квадрат і правильний шестикутник, які мають однакові площі: S3 = S4 = S6 = S. З’ясуємо, у якого з цих многокутників найменший периметр.
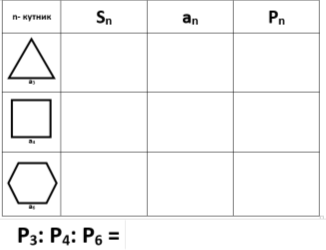

Таким чином, бджолині стільники являють собою просторовий паркет заповнений правильними шестикутниками без прогалин.

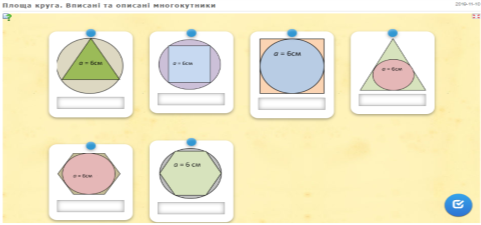
№2 1) А якими ще правильними многокутниками одного виду можна без прогалин заповнити площину? Відповідь обґрунтуйте.
Сума кутів при кожній точці = 360 градусів, тобто градусна міра внутрішнього кута правильного многокутника має бути дільником 360 градусів. Таких мір є три: 120 градусів (правильний шестикутник), 90 градусів ( квадрат), 60 градусів ( правильний трикутник). Відповідні малюнки розглянути
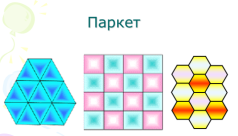
2) Чи можна скласти паркет лише з правильних восьмикутників?
Ні, градусна міра внутрішнього кута правильного восьмикутника 135 градусів, що не є дільником 360 градусів.
 3) Чи можна заповнити площину правильними многокутниками різних видів? Відповідь обґрунтуйте.
3) Чи можна заповнити площину правильними многокутниками різних видів? Відповідь обґрунтуйте.
Щоб площина була заповненою треба, щоб виконувалась умова: сума кутів при одній точці = 360 градусів. І тут кількість роз в’язків велика.
4) Чи можна заповнити площину правильними восьмикутниками та квадратами? Як саме?

№3 Логічна вправа Побудувати візерунок з квадратів і рівносторонніх трикутників, що мають рівні сторони таким чином, щоб вийшов шестикутник і дванадцятикутник.





№4 У кондитерському цеху зробили круглий торт, радіус якого 18см. Для пакування є два види коробок: квадратної форми і форми правильного шестикутника. В яку коробку помістимо торт, якщо сторона квадратної коробки 36см, а шестикутної – 20см?
Розв’язання. Оскільки радіус торта дорівнює 18см, то для розв’язування задачі треба перевірити радіуси вписаних кіл для двох видів коробок.
1) a4 = 36см, r = ![]() = 18см.
= 18см.
2) а6 = 20см, r = ![]() =10
=10![]() =10*1,732
=10*1,732 ![]() 17см.
17см.
Відповідь: торт помістимо в коробку квадратної форми.
№5 Знайди помилку
Із жерсті у вигляді прямокутної трапеції з основами 20см і 30см, та меншою бічною стороною, що дорівнює 20 см вирізали коло. Скільки відсотків жерсті пішло у відходи?


№6 Самостійно розв’язати аналогічну задачу
Із куска алюмінію, який мав вигляд прямокутної трапеції з основами 4 м і 6 м, та меншою бічною стороною, що дорівнює 4 м вирізали коло. Скільки відсотків алюмінію пішло у відходи?

- Підсумок уроку.
Закінчіть фразу:
- Сьогодні на уроці…..
- Тепер я знаю…..
- Мені на уроці……
- Чи справедливий вислів Галілео Галілея: «Математика - це мова, на якій написана книга природи» ?
Дякую всім учням, які взяли активну участь у роботі на уроці, всім, хто відповідав біля дошки (оголошуються оцінки).
- Домашнє завдання.
Д/З Повторити §3 cт 59
Розвязати задачі:
- Чи можна скласти паркет із правильних десятикутників і п'ятикутників? (Відповідь: ні)
- Знайти довжину маятника стінного годинника, якщо кут його коливання становить 38°, а довжина дуги, що описує кінець маятника, дорівнює 24 см. (Відповідь: 36,2 см)
-
Кінець валика діаметром – 4 см обпиляно у вигляді квадрата. Визначте, який найбільший розмір може мати сторона квадрата? . (Відповідь:

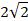 см)
см)

- Обчислити внутрішній кут правильного 5 – кутника.
2. Обчислити радіус кола, вписаного в правильний чотирикутник із стороною 4см.
3.Знайти сторону правильного 6 – кутника, якщо радіус описаного кола навколо нього – 2,5см
4. Радіус кола – 3см. Знайти довжину дуги, якщо ∠АОВ = 60°.

5. Знайти площу кільця, якщо радіус великого кола дорівнює 5 дм, а радіус малого кола – 4 дм

6. Радіус кола – 3см. Знайти площу сектора АОВ, якщо ∠АОВ = 60°.

7. Довжина дуги кола, радіус якого - 30см, дорівнює см. . Знайти градусну міру дуги.
|
2,5 |
3 |
108 |
6 |
9 |
2 |
4 |
|
3 2 |
10 |
|
И |
Б |
П |
А |
О |
Р |
У |
Р |
Д |
Г |
- Обчислити внутрішній кут правильного 5 – кутника.
2. Обчислити радіус кола, вписаного в правильний чотирикутник із стороною 4см.
3.Знайти сторону правильного 6 – кутника, якщо радіус описаного кола навколо нього – 2,5см
4. Радіус кола – 3см. Знайти довжину дуги, якщо ∠АОВ = 60°.

5. Знайти площу кільця, якщо радіус великого кола дорівнює 5 дм, а радіус малого кола – 4 дм

6. Радіус кола – 3см. Знайти площу сектора АОВ, якщо ∠АОВ = 60°.
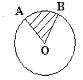
7. Довжина дуги кола, радіус якого - 30см, дорівнює см. . Знайти градусну міру дуги.
|
2,5 |
3 |
108 |
6 |
9 |
2 |
4 |
|
3 2 |
10 |
|
И |
Б |
П |
А |
О |
Р |
У |
Р |
Д |
Г |
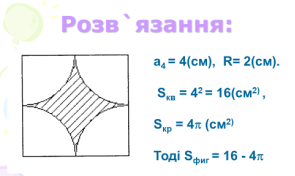
№5 Із жерсті у вигляді прямокутної трапеції з основами 20 см і 30 см, та меншою бічною стороною, що дорівнює 20 см вирізали коло. Скільки відсотків жерсті пішло у відходи?

№6 Із куска алюмінію, який мав вигляд прямокутної трапеції з основами 4 м і 6 м, та меншою бічною стороною, що дорівнює 4 м вирізали коло. Скільки відсотків алюмінію пішло у відходи?

№5 Із жерсті у вигляді прямокутної трапеції з основами 20 см і 30 см, та меншою бічною стороною, що дорівнює 20 см вирізали коло. Скільки відсотків жерсті пішло у відходи?
 №6 Із куска алюмінію, який мав вигляд прямокутної трапеції з основами 4 м і 6 м, та меншою бічною стороною, що дорівнює 4 м вирізали коло. Скільки відсотків алюмінію пішло у відходи?
№6 Із куска алюмінію, який мав вигляд прямокутної трапеції з основами 4 м і 6 м, та меншою бічною стороною, що дорівнює 4 м вирізали коло. Скільки відсотків алюмінію пішло у відходи?

Домашнє завдання Повторити §3 cт 59
Розвязати задачі:
- Чи можна скласти паркет із правильних десятикутників і п'ятикутників?
- Знайти довжину маятника стінного годинника, якщо кут його коливання становить 38°, а довжина дуги, що описує кінець маятника, дорівнює 24 см.
- Кінець валика діаметром – 4 см обпиляно у вигляді квадрата. Визначте, який найбільший розмір може мати сторона квадрата?
Домашнє завдання Повторити §3 cт 59
Розвязати задачі:
- Чи можна скласти паркет із правильних десятикутників і п'ятикутників?
- Знайти довжину маятника стінного годинника, якщо кут його коливання становить 38°, а довжина дуги, що описує кінець маятника, дорівнює 24 см.
- Кінець валика діаметром – 4 см обпиляно у вигляді квадрата. Визначте, який найбільший розмір може мати сторона квадрата?


про публікацію авторської розробки
Додати розробку
