самостійна робота з геометрії 9 класу "Скалярний добуток векторів "
Про матеріал
пропонується самостійна робота з геометрії 9-го класу за темою "Скалярний добуток векторів" в двох варіантах (ІІ семестр 2019-2020 навчального року) до підручника Мерзляка "Геометрія, 9 клас" Перегляд файлу
Самостійна робота з геометрії 9 класу
2019-2020 навчальний рік
Скалярний добуток векторів
І варіант
- Знайдіть скалярний добуток векторів:
-
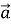 (-2; 1) і
(-2; 1) і 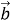 (4; 0) 2)
(4; 0) 2) 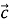 (4; - 9) і
(4; - 9) і 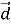 (1; 2 ).
(1; 2 ).
-
Дано вектори
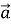 ( -2 ; 4 ) і
( -2 ; 4 ) і 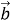 ( х; 5 ). При якому значенні х добуток
( х; 5 ). При якому значенні х добуток
![]() ·
· ![]() = 12?
= 12?
-
φ – кут між векторами
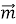 і
і 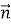 . Знайдіть
. Знайдіть 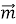 ·
· 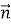 , якщо |
, якщо | 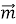 |= 1; |
|= 1; | 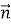 | = 8;
| = 8;
φ = 120º.
-
Чи перпендикулярні вектори
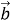 і
і 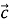 , якщо:
, якщо:
-
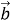 (-4; 8) і
(-4; 8) і 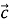 (10; 5); 2)
(10; 5); 2) 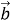 (4; -3 ) і
(4; -3 ) і 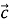 (5; 6 )?
(5; 6 )?
-
Знайдіть косинус кута між векторами
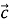 (-4; 3) і
(-4; 3) і 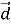 (15; - 8 ).
(15; - 8 ).
- Знайдіть кути трикутника АВС, якщо А ( -2; 1), В ( 1; 5 ), С ( 5; 2 ).
-
Знайдіть косинус кута, який утворюють вектори
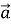 і
і 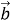 , якщо
, якщо
| ![]() |= |
|= | ![]() |= 1; (
|= 1; ( ![]() - 2
- 2![]() ) ( 3
) ( 3![]() +
+ ![]() ) = 4.
) = 4.
ІІ варіант
- Знайдіть скалярний добуток векторів:
-
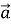 ( 0; 3) і
( 0; 3) і 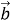 ( 4; -1); 2)
( 4; -1); 2) 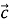 (-2; 5) і
(-2; 5) і 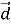 (-1; 3 ).
(-1; 3 ).
-
Дано вектори
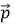
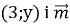 (-6; 2). При якому значенні у добуток
(-6; 2). При якому значенні у добуток
![]() ·
· ![]() = -6?
= -6?
-
φ – кут між векторами
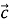 і
і 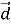 . Знайдіть
. Знайдіть 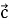 ·
· 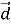 , якщо |
, якщо | 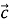 |= 5√3, |
|= 5√3, | 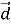 | = 1,
| = 1,
φ = 150º.
-
Чи перпендикулярні вектори
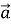 і
і 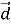 , якщо:
, якщо:
-
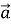 (4; -2) і
(4; -2) і 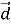 ( 10; 15); 2)
( 10; 15); 2) 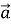 ( -2; -1) і
( -2; -1) і 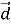 (5; - 10)?
(5; - 10)?
-
Знайдіть косинус кута між векторами
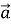 (6; -8) і
(6; -8) і 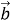 ( 12; 5).
( 12; 5).
- Знайдіть косинуси кутів трикутника АВС, якщо А (-3; 1), В (1; 4),
С (5; 1).
-
Знайдіть косинус кута, який утворюють вектори
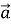 і
і 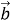 , якщо
, якщо
| ![]() |= |
|= |![]() |=1; (
|=1; ( ![]() + 2
+ 2![]() ) (3
) (3![]() -
- ![]() ) = 5.
) = 5.
Середня оцінка розробки
Оцінки та відгуки
docx
До підручника
Геометрія 9 клас (Мерзляк А. Г., Полонський В. Б., Якір М. С)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку

-

Шмагун Наталія
12.12.2023 в 20:54
Щиро дякую!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Гура Олена Федорівна
05.12.2023 в 07:20
Дякую. Чудова допомога.
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Чередніченко Світлана
27.04.2023 в 14:09
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Соколова Елена
07.02.2022 в 22:16
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Чайнікова Наталія Анатоліівна
07.12.2021 в 20:53
Загальна:
4.3
Структурованість
5.0
Оригінальність викладу
3.0
Відповідність темі
5.0
-

Стельмах Оксана Анатоліївна
23.11.2021 в 21:39
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Кордіс Алла Олександрівна
10.11.2021 в 16:28
Загальна:
4.0
Структурованість
4.0
Оригінальність викладу
3.0
Відповідність темі
5.0
-

Безверхний Николай
08.02.2021 в 20:46
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 5 відгуків