Тема уроку:   Многогранники. Розв’язування задач прикладного змісту

Мета уроку:   формувати вміння розв’язувати прикладні задачі на знаходження   об’ємів призм, використовувати формули площ многокутників; розвивати вміння учнів створювати математичні моделі до задач, показати роль математичних знань в житті людини,  необхідність знань для задоволення практичних потреб; виховувати навички співпраці.

Обладнання:    комп’ютер, проектор,  вимірювальні прилади, картки з формулами, вислови відоми  людей.

Тип уроку:   Формування умінь і навичок

Х і д   у р о к у.

1. Організаційний момент.

Добрий день, шановні одинадцятикласники! Щиро вітаємо наших гостей!

Людина проявляє інтерес до многогранників на протязі всієї своєї свідомої діяльності – від дворічної дитини , що грається деревинними кубиками, до зрілого математика, який насолоджується читанням книжок про многогранники. Сьогодні на уроці ми дізнаємося: де, навіщо і для чого нам потрібно обчислювати площі та об’єми  многогранників? 

Сьогодні ми з вами поговоримо на досить цікаву тему «Прикладні математичні задачі».  Задачі нематематичного змісту, які можна розв’язувати математичними методами, досить часто зустрічаються в нашому повсякденному житті. Це і обчислення відстаней, площ під час ремонту, обчислення об’ємів та площ поверхонь різних архітектурних об’єктів. Саме про обчислення об’ємів ми сьогодні й поговоримо.

2. Актуалізація вивченого матеріалу.

Асоціативний кущ.

 Назвіть якомога більше тлумачень слова «призма».

Відповідь: призма:

•                   тип многогранника;
•                   вигляд архітектурної споруди;
•                   головоломка, кубик Рубика;
•                   в природі тригранні, безлисті до самої верхівки стебла папірусу досягають 4-5 м у висоту і до 7 см в діаметрі.

Метод  «Мозковий штурм»

1. Пригадайте як обчислюється об’єм призми

V = S_оснН, V = abc.

2. Що таке Н? Чим є висота прямої призми?
3. Які многокутники можуть бути основою призми?
4. Давайте пригадаємо формули площ?

Вправа «Аукціон».

Продається площа многокутника. Ваша задача – пригадати якомога більше формул для обчислення площ.

(учні називають формули)

Усний рахунок

1.   Якщо ребро куба дорівнює 3 см, то його повна  площа поверхні дорівнює:

В. 54 см.

2. Якщо виміри прямокутного паралелепіпеда 3 см, 2 см та 6 см, то площа найбільшої грані дорівнює:           В) 18 см.

3) Об’єм куба з ребром 4 см      В. 64

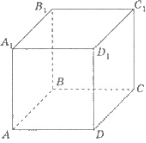4) .  . На малюнку  зображено прямокутний паралелепіпед АВСDА₁В₁С₁D₁, АВ = 1, АD= 2, АА₁= 2. Установити відповідність між геометричними величинами (1-4) та їхніми числовими значеннями (А-Д).

1 Відстань між мимобіжними прямими АА₁ і DС.

2 Довжина діагоналі прямокутного паралелепіпеда.

3 Площа повної поверхні прямокутного паралелепіпеда.

4 Площа бічної поверхні прямокутного паралелепіпеда.

А 16.

Б 12.

В 4.

Г 3.

Д 2.                                 

1 - Д, 2 - Г, 3 - А, 4 - Б

5) У кого більше ребер – у двох паралелепіпедів чи в одного учня?(однакова)

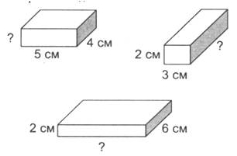
6) Відомо, що об'єм кожного із зображених на рис. прямокутного паралелепіпеда дорівнює 60 см². Знайдіть невідомий вимір кожного прямокутного паралелепіпеда.

6) Наш кабінет математики  має такі розміри: 9 × 6 × 2,8 м:

Знайти об’єм повітря в кабінеті. (151,2

3. Повідомлення теми і мети уроку.

     Сьогодні на уроці ми навчимося розв’язувати прикладні задачі на знаходження об’ємів призм,  використовувати формули площ многокутників; створювати математичні моделі до задач.

     Ми разом з вами розглянемо приклади обчислення  площі, об’єму призми в певних життєвих ситуаціях як на сучасному етапі так і в професійному  контексті.

4. Задача за готовим малюнком

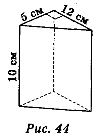
1) Бічне ребро прямої призми дорівнює 10 см, а в основі лежить:

варіант 1 — прямокутний трикутник з катетами 12 і 5 см (рис. 44);

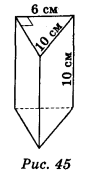
варіант 2 — прямокутний трикутник з гіпотенузою 10 см і катетом 6 см (рис. 45). Знайдіть:

а) довжину третього ребра основи; (1 бал)

б) площу основи; (1 бал)

в) площу бічної поверхні призми; (1 бал)

г) площу повної поверхні призми; (1 бал)

д) діагональ найбільшої бічної грані. (1 бал)

е) об’єм  призми. (1 бал)

Відповідь.

Варіант 1. 1) а) 13 см; б) 30 см²; в) 300 см²; г) 360 см²; д) см; е) 300 см³

Варіант 2. 1) а) 8 см; б) 24 см²; в) 240 см²; г) 288 см²; д) 10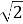 см; е) 240 см³. 

 Практичний блок «У світі професій» - Робота в групах

Фасовщик

• У кондитерський цех надійшли ящики для цукерок Гулівер. Чи помістяться в ящик розміром 38×29×11 см.
• а) 200шт,
• б) 300 шт.
• (дітям роздаються цукерки Гулівер, розміри одного Гулівера 8×3,5×2 см, діти вимірюють самостійно)
•  Розв'язання
• Для розв'язання задачі необхідно побачити, що цукерка має форму прямокутного паралелепіпеда.
• V₁=a₁b₁c₁, V₁=38∙29∙11=12122 (см³)
• V₂=a₂b₂c₂, V₂=8∙3,5∙2=56 (см³)
• V₁/V₂=12122/56≈216 (шт)
• Отже: а) 200 шт. помістяться, б) 300 шт. не помістяться.
• Відповідь: а) Так, б) ні.

Працівники харчоблоку

У їдальню завезли ящик масла розмірами 50×35×20 см і розрізали його на кубики з ребром - 2,5 см. На яку кількість дітей вистачить масла, якщо на сніданок подають на 1 дитину - 1 кубик.

Розв'язання

V=SH

V_я=abc, V_я=50∙35∙20=35000(см³)

V_k=x³, V_k=2,5³=15,625 (см³)

V_я/V_k=35000/15,625=2240 (діт.)

Відповідь: 2240 дітей.

Кондитери

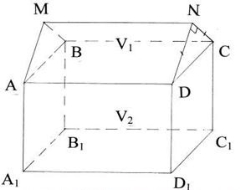• Дівчата спекли торт у вигляді будиночка. Знайдіть його об'єм, якщо довжина торта 35 см, ширина 20 см, висота стін 10 см, а скати даху становлять кут 90^о.
•  
•  
•  
•  
•  
•  
•  
•  
•  
• Розв'язання
• Будиночок складається із двох геометричних фігур, трикутної призми і прямокутного паралелепіпеда. Отже його об'єм дорівнює сумі двох об'ємів.
• V=V₁+V₂
• 1)V₁=SH; S=0,5NC∙ND
• Нехай CN = ND = x трикутник CND прямокутний за умовою, тоді
• 20²=х²+х²
• 2х²=400
• х²=200
• x=10√2, отже CN=ND=10√2 см
• S=0,5x²=0,5∙200=100 (см²), H=AD=35 см.
• V₁=100∙35=3500(см³)
• 2) V₂=35∙20∙10=7000(см³)
• 3) V=3500+700=10500(см³)
• Відповідь: 10500 см³

6.  Колективна робота . ПІДПРИЄМЕЦЬ

    Відомо, що для нашого міста є актуальною проблема питної води. Тому жителі користуються привозною водою .  Воду завозять два підприємці, вартість бочки води в першого – 180 грн, у другого – 210 грн. Скажіть, у кого з підприємців вигідніше купувати воду, якщо при завозі води першим підприємцем, в резервуар  для води розмірами 2×2×2,5 м не долито 50 см води, а при завозі другим підприємцем – 30 см.

7. Практична робота ( робота в парах ) АРХІТЕКТОРИ

 Кожна пара отримує многогранник

Повідомлення результатів.

А зараз я попрошу вас обмінятися картами самооцінювання і оцінити роботу в парі свого партнера.

8.               Кожний з вас уже визначився із своєю майбутньою професією, і можливо сьогодні через розв’язання задач мені ще раз вдалося підкреслити, що математика повсюди.  Кожна професія потрібна, важлива, а найголовніше, щоб вона була до душі….. А це залежить сьогодні тільки від вас, де ви будете навчатися, 21 травня не за горами…… і я пропоную, оцінити свої знання уже зараз

ЗНО

Самоперевірка

9. Підведення підсумків уроку. Рефлексія.

І на останок  пропоную Вам використати свої знання з рідної мови і поставити вірно знаки в наступному реченні.  Сподіваюсь, що цим ви також підкреслите важливість вивченої теми.

Забути не можна пам’ятати

Очікуваний результат –   Забути не можна, пам’ятати!

VII. Домашнє завдання

Обчислити повні площі шафи і коробки сірників.

А закінчити заняття я хотіла би словами нашого великого співвітчизника видатного педагога Василя Олександровича  Сухомлинського: “Математика вчить мислити й разом з тим вселяє віру в безмежні сили людського розуму . Вона виховує волю, характер.”

ОЦІНОЧНИЙ ЛИСТ    11 – А клас       __________________________