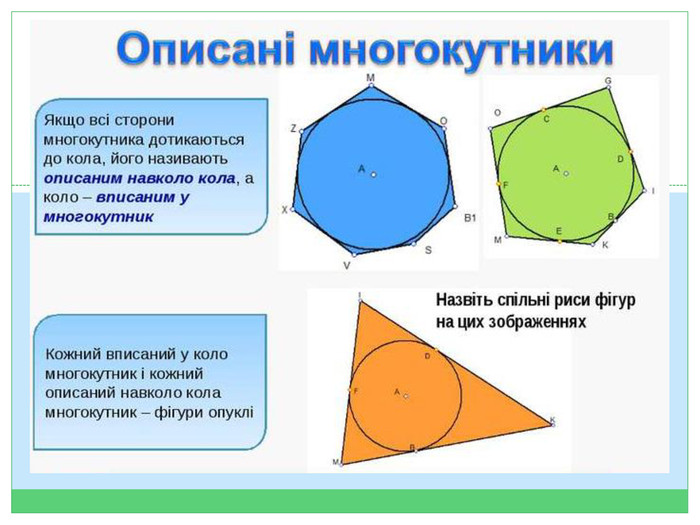
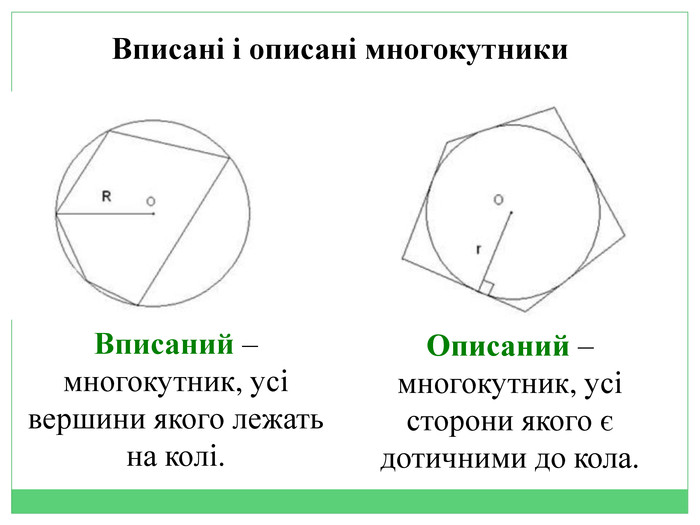
Многокутник, вписаний у коло. Многокутник, описаний навколо кола
Про матеріал
Презентація до уроку геометрії у 8 класі з теми "Многокутник, вписаний у коло. Многокутник, описаний навколо кола". Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку