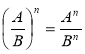Множення дробів. Піднесення дробу до степеня
Тема. Множення дробів. Піднесення дробу до степеня
Мета: домогтися засвоєння учнями змісту та схеми доведення правила множення раціональних дробів, а також змісту алгоритму (орієнтовної схеми дій) множення раціональних дробів; формувати вміння відтворювати вивчені правила й алгоритм та застосовувати їх під час виконання завдань на множення раціональних дробів; вдосконалювати вміння виконувати скорочення раціональних дробів та знаходити ОДЗ дробового виразу.
Тин уроку: засвоєння знань, формування первинних умінь.
Наочність та обладнання: опорний конспект «Множення і ділення раціональних дробів».
Хід уроку
I. Організаційний етан
На цьому етапі уроку слід надати учням інформацію:
- про орієнтовний план вивчення розділу;
- кількість навчальних годин;
- приблизний зміст матеріалу;
- основні вимоги до знань та вмінь учнів;
- орієнтовний зміст завдань, що будуть винесені на контроль.
(Цю інформацію можна помістити на стенді «Довідково-інформаційний куточок» у кабінеті математики та задля економії часу запропонувати учням для самостійного ознайомлення в позаурочний час).
II. Перевірка домашнього завдання
Письмова частина домашнього завдання (аналіз контрольної роботи) перевіряється вчителем після того, як він збере зошити учнів для перевірки.
Якість виконання учнями усної частини домашнього завдання перевіряється під час виконання усних вправ. Цю роботу можна провести у формі математичного диктанту на повторення.
III. Формулювання мети і завдань уроку, мотивація навчальної діяльності учнів
IV. Актуалізація опорних знань та вмінь
Для успішного сприйняття учнями навчального матеріалу уроку перед вивченням нового матеріалу слід активізувати знання і вміння учнів щодо правила множення та скорочення звичайних дробів, основної властивості степеня та її наслідків, розкладання многочленів на множники, скорочення раціональних дробів та правила знаків для раціональних дробів.
Виконання усних вправ
-
Обчисліть:
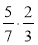 ;
; 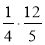 ;
; 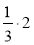 ;
; 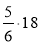 ;
; 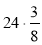 ;
; 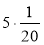 .
.
- Подайте у вигляді степеня з основою у вирази:
у ∙ у3; у10 ∙ у2; ![]() ;
; ![]() ; у18 ∙ у2;
; у18 ∙ у2; ![]() ;
; ![]() .
.
- Розкладіть вираз на множники:
а) ах – а; б) х2 + 1 – 2х; в) х2 + 8х; г) 2у2 – 8; д) у3 – x2y; е) k3 – x3;
ж) 4х2 + 16х + 16; з) 27 + 3у2 – 18у.
- Яких значень (рівних чи протилежних) набувають при одному й тому самому значенні змінної вирази:
а) – х і х; б) х – 2 і 2 – х; в) ![]() і
і ![]() ; г)
; г) ![]() і
і ![]() ; д)
; д) ![]() і
і ![]() ; є)
; є) ![]() і
і ![]() ?
?
V. Засвоєння знань
План вивчення нового матеріалу
- Правило множення раціональних дробів (із доведенням).
- Алгоритм множення раціональних дробів; приклади його застосування.
Традиційно вивчення питання про перетворення добутку раціональних дробів на раціональний дріб починається із формулювання правила множення раціональних дробів у словесній формі та у вигляді формули
![]()
(яка справджується при всіх допустимих значеннях змінних). Справедливість цієї формули доводиться шляхом міркувань, що грунтуються на уявленні про дріб як особливу форму запису частки двох виразів та на властивостях компонентів дії ділення (як в доведенні правил додавання і віднімання раціональних дробів та основної властивості дробу).
Так само як під час вивчення додавання і віднімання раціональних дробів після доведення справедливості правила множення раціональних дробів, на основі цього правила складається схема (алгоритм) виконання дій, які мають привести від добутку раціональних дробів до раціонального дробу.
Застосування складеного алгоритму слід продемонструвати на різнопланових прикладах.
Для більшої наочності на уроці служить опорний конспект «Дії над раціональними дробами».
|
Конспект 4 |
||
|
Множення і ділення раціональних дробів |
||
|
|
1. Для будь-яких А, В, С і D де В ≠ 0, D ≠ 0, справджується рівність:
|
|
|
|
||
|
|
2. Для будь-яких А і В, В ≠ 0, справджується рівність:
|
|
|
|
||
|
|
3. Для будь-яких А, В, С і D де B ≠ 0, C ≠ 0, D ≠ 0, справджується рівність: |
|
|
Зауваження. Дріб, яким записується добуток або частка дробів необхідно (якщо це можливо) скоротити! Записувати його раціональним дробом — тільки виходячи з умови завдання |
||
VI. Формування вмінь
Виконання усних вправ
- Прокоментуйте (згідно з алгоритмом) виконання дій у виразах:
а) ![]() ;
;
б) 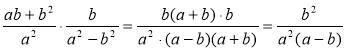 .
.
- Подайте у вигляді дробу вираз:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() ; є)
; є) ![]() .
.
-
При а =
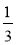 знайдіть значення виразів:
знайдіть значення виразів: 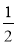 а;
а; 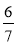 а;
а; 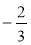 а;
а; 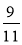 а.
а.
Виконання письмових вправ
Для реалізації дидактичної мети уроку слід розв'язати завдання такого змісту:
- Множення раціональних дробів (у різних ситуаціях: на пряме застосування правила множення раціональних дробів, із можливістю скорочення раціонального дробу, із необхідністю розкладання многочленів у чисельнику та знаменнику дробу на множники, для випадку як двох, так і більшої кількості множників).
1) Виконайте множення: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) 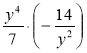 ;
;
д) ![]() ; е)
; е) 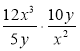 ; ж)
; ж) ![]() ; з)
; з) 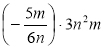 .
.
2) Виконайте множення: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ;
;
д) ![]() ; є)
; є) ![]() ; ж)
; ж) ![]() ; з)
; з) ![]() .
.
3) Спростіть вираз: а) 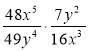 ; б)
; б) ![]() ; в)
; в) 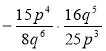 ;
;
г) 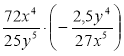 ; д)
; д) 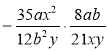 ; є)
; є) 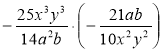 .
.
4) Виконайте множення: а) 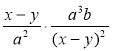 ; б)
; б) ![]() ;
;
в) 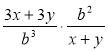 ; г)
; г) ![]() ; д)
; д) ![]() ; є)
; є) ![]() .
.
5) Спростіть вираз:
а) ![]() ; б)
; б) 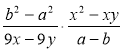 ; в)
; в) 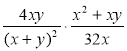 ;
;
г) 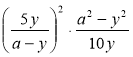 ; д)
; д) ![]() ; є)
; є) 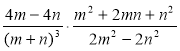 ;
;
ж) 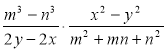 ; з)
; з) ![]() .
.
6) Виконайте множення:
а) 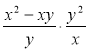 ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ;
;
д) ![]() ; є)
; є) 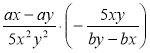 .
.
- Виконання вправ на повторення: додавання (віднімання) раціональних дробів з однаковими та різними знаменниками.
1) Подайте вираз у вигляді дробу:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ;
;
г) ![]() ; д)
; д) 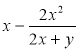 ; є)
; є) ![]() .
.
2) Спростіть вираз:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
3) Спростіть вираз:
а) ![]() ; б)
; б) ![]() ;
;
в) 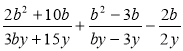 ; г)
; г) ![]() ;
;
д) ![]() ; є)
; є) ![]() ;
;
ж) ![]() ; з)
; з) ![]() .
.
- Виконання логічних вправ та завдань підвищеного рівня складності для учнів, які мають достатній та високий рівні знань.
1) Виконайте множення:
а) ![]() ; б)
; б) ![]() .
.
2) Спростіть вираз:
а) ![]() ; б)
; б) ![]() .
.
3) Виконайте дії:
а) ![]() ; б)
; б) ![]() .
.
4) Який запис пропущено:
|
|
|
|
|
? |
Вправи, запропоновані для розв'язування на урок, мають бути спрямовані на засвоєння навичок швидкого та безпомилкового перетворення добутку двох раціональних дробів у раціональний дріб. Цього можна домогтися за рахунок достатньо великої кількості вправ різного рівня складності (див. вище).
Слід зауважити, що в перетворенні добутку раціональних дробів широко використовуються: формули скороченого множення, правило зміни знака дробу, різні прийоми розкладання многочленів на множники. Під час усної роботи на уроках корисно пропонувати учням вправи на повторення цих моментів.
Звернімо увагу також на те, що було б помилкою під час вивчення множення раціональних дробів виконувати вправи тільки на множення, відмовившись від виконання дій додавання і віднімання раціональних дробів та від порівняння правил виконання цих дій. Для формування сталих навичок виконання додавання і віднімання раціональних дробів (як відомо, це потребує досить великого проміжку часу) у ході вивчення як множення, так і ділення раціональних дробів через систему усних та повторювальних вправ слід продовжувати роботу з удосконалення вмінь учнів виконувати додавання і віднімання раціональних дробів.
VII. Підсумки уроку
В якому з випадків правильно виконано множення раціональних дробів?
а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ?
?
VIII. Домашнє завдання
- Вивчити правило множення раціональних дробів (із доведенням).
- Розв'язати вправи на засвоєння алгоритму множення раціональних дробів та відпрацювання навичок його застосування.
- Розв'язати вправи на повторення алгоритмів додавання і віднімання раціональних дробів.
- Повторити правило множення звичайного дробу на ціле число (довідник, 6 клас), означення і властивості степеня з натуральним Показником та властивості множення звичайних дробів (переставну, сполучну і розподільну).


про публікацію авторської розробки
Додати розробку