Множення дробів. Піднесення дробу до степеня
Тема. Множення дробів. Піднесення дробу до степеня
Мета: домогтися засвоєння учнями схеми дій під час множення раціонального дробу на цілий вираз, а також алгоритму піднесення раціонального дробу до натурального степеня та виконання сумісних дій піднесення дробу до степеня та множення раціональних дробів; сформувати вміння свідомо відтворювати вивчені схеми, а також виконувати дії за цими схемами під час виконання відповідних перетворень раціональних виразів.
Тип уроку: застосування знань, умінь та навичок.
Наочність та обладнання: опорний конспект «Множення і ділення раціональних дробів».
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
Перевірку виконання вправ домашнього завдання можна здійснити за зразком.
Для учнів, які добре засвоїли матеріал попереднього уроку, можна запропонувати індивідуальні завдання (змісту, аналогічного до вправ домашнього завдання або з елементами нестандартності).
III. Формулювання теми і завдань уроку
За умови усвідомлення учнями існування певної аналогії між алгоритмами виконання арифметичних дій зі звичайними та раціональними дробами, під час перевірки останньої частини домашнього завдання (див. 4 пункт домашнього завдання попереднього уроку) учні мають передбачити навчальну ситуацію, що буде розглянута на поточному уроці: випадок множення раціонального дробу на цілий вираз, а також множення раціональних виразів із застосуванням властивостей множення.
Названі «проблемні ситуації» (протиріччя між набутими раніше знаннями та існуючою ситуацією) мають бути розв'язані. Це і є основною дидактичною метою уроку.
IV. Актуалізація опорних знань та вмінь
Відповідно до мети уроку перед вивченням питання про множення раціонального дробу на цілий вираз піднесення раціонального дробу до степеня слід активізувати знання і вміння учнів щодо способу подання цілого числа (виразу) у вигляді дробу із заданим знаменником, виконання дії множення цілого числа на звичайний дріб, основної властивості степеня та її наслідків (особливо піднесення дробу і добутку до степеня), а також перетворень раціональних дробів, вивчених на попередніх уроках.
Виконання усних вправ
-
Обчисліть:
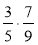 ;
; 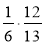 ;
; 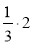 ;
; 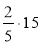 ;
; 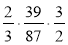 ;
; 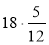 ;
; 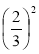 ;
; 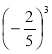 .
.
- Розкладіть на множники вираз:
а) тх – т; б) т2 + п2 – 2тп; в) х – у + 2х – 2у;
г) т2 – п2; д) 14п2 – 14; є) 2т3 – 16.
- Подайте вирази у вигляді дробу:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() ;
;
є) ![]() ; ж)
; ж) ![]() ; з)
; з) ![]() ; и)
; и) ![]() .
.
- Спростіть вирази: (2х)2; (-3х)2; (х2)3; (3х2)3; а2 – 2ab)3.
V. Засвоєння знань
План вивчення нового матеріалу
- Алгоритм множення раціонального дробу на цілий вираз.
- Правило піднесення дробу до степеня (із доведенням). Алгоритм піднесення дробу до степеня.
- Алгоритм виконання дій у більш складних виразах, шо містять кілька дій.
- Приклади застосування складених алгоритмів.
Правило виконання множення раціонального дробу на цілий вираз має таку саму форму, як і правило множення звичайного дробу на ціле число: воно виражається формулою ![]() (це правило множення звичайних дробів учні вивчали за підручником «Математика, 5 клас», автори: Мерзляк А. Г. та інші). Згідно з цією формулою учні мають скласти схему дій під час виконання такого перетворення у загальному випадку.
(це правило множення звичайних дробів учні вивчали за підручником «Математика, 5 клас», автори: Мерзляк А. Г. та інші). Згідно з цією формулою учні мають скласти схему дій під час виконання такого перетворення у загальному випадку.
Доведення тотожності 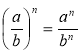 спирається на означення степеня з натуральним показником та на правило множення раціональних дробів. Тому це доведення учні можуть провести самостійно, а також самостійно скласти орієнтовну схему виконання цієї дії.
спирається на означення степеня з натуральним показником та на правило множення раціональних дробів. Тому це доведення учні можуть провести самостійно, а також самостійно скласти орієнтовну схему виконання цієї дії.
Що стосується більш складних випадків (у виразі міститься відразу дві та більше дій), то учням слід нагадати про існування поняття арифметичних дій і про послідовність виконання дій різного ступеня (від найстаршого до найнижчого ступенів за умови існування або відсутності дужок, що змінюють порядок виконання дій).
Закінчити вивчення матеріалу уроку слід наведенням відповідних прикладів на застосування вивчених схем дій (з одночасним коментарем).
VI. Формування вмінь
Виконання усних вправ
- Прокоментуйте виконання дій у виразі:
а) ![]() ;
;
б) 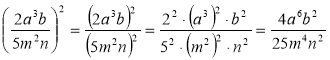 .
.
-
Подайте вирази у вигляді дробу: а)
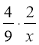 ; б)
; б) 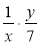 ; в)
; в) 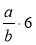 ; г)
; г) 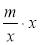 ;
;
д) ![]() ; є)
; є) ![]() ; ж)
; ж) ![]() ; з)
; з) ![]() ; и)
; и) 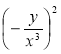 .
.
-
Визначте послідовність виконання дій:
а)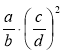 ; б)
; б) 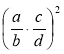 ; в)
; в) 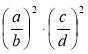 ; г)
; г) 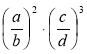 .
.
Виконання письмових вправ
Для реалізації дидактичної мети уроку слід розв'язати завдання такого змісту.
- Множення раціональних дробів на цілий вираз (різного ступеня складності).
1) Подайте у вигляді дробу: ![]() .
.
2) Виконайте множення: ![]() .
.
3) Перетворіть у дріб вираз:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
4) Подайте у вигляді дробу: а) ![]() ; б)
; б) ![]() .
.
5) Виконайте множення: а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
- Піднесення раціонального дробу до степеня.
1) Піднесіть до степеня:
а) 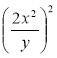 ; б)
; б) 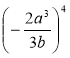 ; в)
; в) 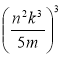 ; г)
; г)  .
.
2) Піднесіть до степеня: а) ![]() ; б)
; б) ![]() ; в)
; в) 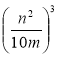 ; г)
; г) 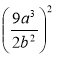 .
.
3) Піднесіть до степеня: а) 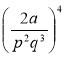 ; б)
; б) 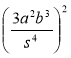 ; в)
; в) 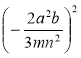 ; г)
; г) 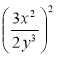 .
.
-
Спрощення виразів (передбачає виконання перетворень раціональ
них виразів, що містять кілька арифметичних дій одного ступеня,
або більше, ніж два множники).
1) Виконайте множення:
а) ![]() ; б)
; б) 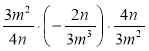 ; в)
; в) ![]() ;
;
г) 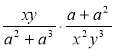 ; д)
; д) ![]() ; є)
; є) ![]() .
.
2) Спростіть вираз 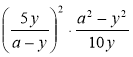 .
.
3) Спростіть вираз: а) 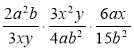 ; б)
; б) 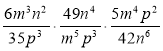 .
.
-
Обчислення значень виразу з попереднім спрощенням його за вив
ченими раніше та на даному уроці схемами.
1) Знайдіть значення виразу ![]() при х = -1; х = 5; х =
при х = -1; х = 5; х = ![]() .
.
2) Знайдіть значення виразу;
а) ![]() , якщо т =
, якщо т = ![]() , п = -3;
, п = -3;
б) ![]() , якщо х = 0,5; -1,5.
, якщо х = 0,5; -1,5.
-
Виконання вправ на повторення: перетворити суму або різницю
раціональних дробів на раціональний дріб.
Спростіть вираз:
а) ![]() ;
;
б) ![]() .
.
-
Виконання логічних вправ та завдань підвищеного рівня складнос
ті для учнів, які мають достатній та високий рівні знань.
1) Знайдіть значення виразу 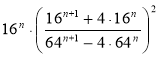 при п = 74; п = 1000.
при п = 74; п = 1000.
2) Спростіть вираз: а) ![]() ; б)
; б) ![]() ;
;
в) 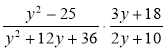 ; г)
; г) ![]() .
.
3) Виключіть зайву пару чисел:
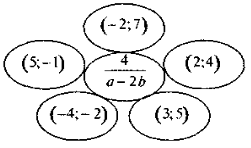
Вправи, запропоновані для розв'язання на урок, мають бути спрямовані на формування навичок швидкого та безпомилкового перетворення добутку раціонального дробу на цілий вираз у раціональний дріб, степеня раціонального дробу у раціональний дріб, а також перетворення «комбінованих» виразів у раціональний дріб. Цього можна домогтися за рахунок достатньо великої кількості вправ різного рівня складності (див. вище).
Так само як і на попередньому уроці, виконання перетворень раціональних виразів супроводжується широким використанням формул скороченого множення, правила зміни знака дробу, різних способів розкладання многочленів на множники. Під час усної роботи на уроках корисно пропонувати учням вправи на повторення цих моментів.
Також не слід забувати про необхідність подальшого відпрацювання навичок виконання множення раціональних дробів та дій додавання і віднімання раціональних дробів. Ця робота проводиться через систему усних та повторювальних вправ.
VII. Підсумки уроку
В якому з випадків правильно виконано дію з раціональними дробами?
а) ![]() ; б)
; б) 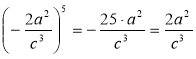 ;
;
в) 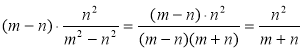 ; г)
; г) 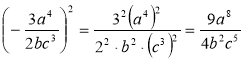 .
.
VIII. Домашнє завдання
- Вивчити алгоритми виконання дій, складених та опрацьованих на уроці.
- Розв'язати завдання на формування навичок використання вивчених алгоритмів.
- На повторення: вправи на виконання дій із раціональними дробами.


про публікацію авторської розробки
Додати розробку
