Множення вектора на число. Колінеарні вектори.

Тема уроку. Множення вектора на число. Колінеарні вектори.

Мета уроку: формування вміння множити вектор на число; вивчення властивостей множення вектора на число та ознак колінеарних векторів; формуван­ня вмінь застосовувати вивчені властивості до розв'язування задач.

Тип уроку: комбінований.

Обладнання: презентація, комплекс ІКТ, лінійка, кольорова крейда.

Вимоги до рівня підготовки учнів: описують множення вектора на число; відкладають вектор, що дорівнює добутку вектора на число; описують колінеарність векторів; застосовують вивчені ознаки та властивості до розв'язування задач.

Хід уроку

1. Організація класу

Учні готують все необхідне до уроку.

Пропоную учням уважно розглянути зображення на слайді: «Що зображено на малюнку?»

Висновок: від того наскільки уважно ми розглядаємо малюнок, залежить скільки нових елементів ми бачимо на ньому. Тому будьте уважними та зосередженими протягом усього уроку, щоб якомога більше дізнатися та засвоїти матеріал.

ІI. Перевірка домашнього завдання

Перевірити наявність виконаного домашнього завдання та від­повісти на запитання, які виникли в учнів при його виконанні.

3. Актуалізація опорних знань

1. Виберіть правильне твердження

1.Вектор – це…

а) напрямлений відрізок;

б) відрізок, що має координати

в) пряма, що має напрям.

2. Нульовий вектор – це …

а) вектор абсолютна величина якого не існує;

б) вектор у якого початок співпадає з його кінцем;

в) вектор, що немає ні початку ні кінця.

3. Сума двох векторів дорівнює одному з векторів-доданків якщо

а) початок співпадає з його кінцем;

б) обидва вектори нульові;

в) один із векторів нульовий вектор.

4. Сума двох векторів дорівнює нулю, якщо….

а) вектори протилежно напрямлені;

б) один із векторів нульовий;

в) виходять з однієї точки.

2. Математичний диктант

Дано вектори:

Варіант 1   Варіант 2

(3; 0); (7; 4)  (-2; 2); (1; 6)

Запишіть:

а) координати вектора + ;

б) координати вектора – ;

в) координати вектора – ;

г) довжину вектора – .

Перевірка диктанту:

Учні повторюють правила додавання і віднімання векторів.

4. Повідомлення теми і мети уроку

Тема уроку. Множення вектора на число. Колінеарні вектори.

Ця тема є важливою для вивчення, бо включається в програму ЗНО.

Сьогодні на уроці:

- навчимося множити вектор на число;

- вивчимо властивості множення вектора на число та ознаки колінеарних векторів;

- сформуємо вміння застосовувати вивчені властивості до розв’язування задач.

V. Поетапне сприймання й усвідомлення нового матеріалу

Множення вектора на число

Добутком вектора на дійсне число k називаєтеся вектор = k,  колінеарний вектору , причому:

1. = |k| · ;
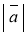2. якщо k > 0, то вектор 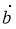однаково напрямлений з вектором ;
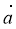3. якщо k < 0, то вектор 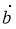протилежно напрям­лений вектору 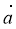(рис. 209).

Властивості добутку вектора на число

1. (k₁k₂) 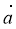= k₁(k₂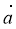) (сполучний закон);
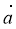2. k₁ + k₂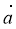 = (k₁ + k₂) 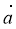(розподільний закон);
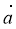3. k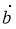 + k = k(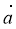 + 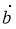) (розподільний закон);

Два ненульові вектори та колінеарні тоді та тільки тоді, коли = k, k — відмінне від нуля число.

Координати вектора k дорівнюють добутку числа k на від­повідні координати вектора . Якщо вектори задано на площині, то k(а₁; а₂) = (kа₁; kа₂).

Ознаки колінеарності:

Наслідок 1:вектори а(а₁;а₂) і b(ka₁;ka₂) колінеарні.

Наслідок 2: якщо вектори а(а₁;а₂) і b (b₁;b₂) колінеарні, то існує таке число k, що b₁= ka₁ і b₂= ka_2.

Якщо вектори колінеарні, то їхні відповідні координати про­порційні. І навпаки, якщо відповідні координати двох векторів пропорційні, то ці вектори колінеарні.

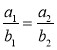Якщо вектори (a₁; a₂) і (b₁; b₂) колінеарні, то . Якщо 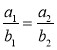і (a₁; a₂), (b₁; b₂), то вектори і колінеарні.

ІІІ. Закріплення й осмислення нового матеріалу

Розв'язування вправ

1. Побудуйте вектор 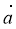, довжина якого дорівнює 4 см. Побудуй­ те за допомогою лінійки вектори:

а) 2;  б) -.

2. Дано 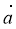(1; -3), 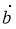(-2; 1). Знайдіть координати вектора:

а) 2;  б) -3; в) 2 – 3.

3. Знайдіть |2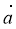|, якщо 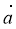(1; 2).
4. Доведіть, що вектори 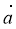(1; 2) і 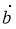(0,5; 1) однаково напрямлені, а вектори 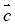(-1; 2) і 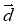(0,5; -1) протилежно напрямлені.

V. Підбиття підсумків уроку
 

IV. Домашнє завдання