Презентація "Осьова симетрія"
Про матеріал
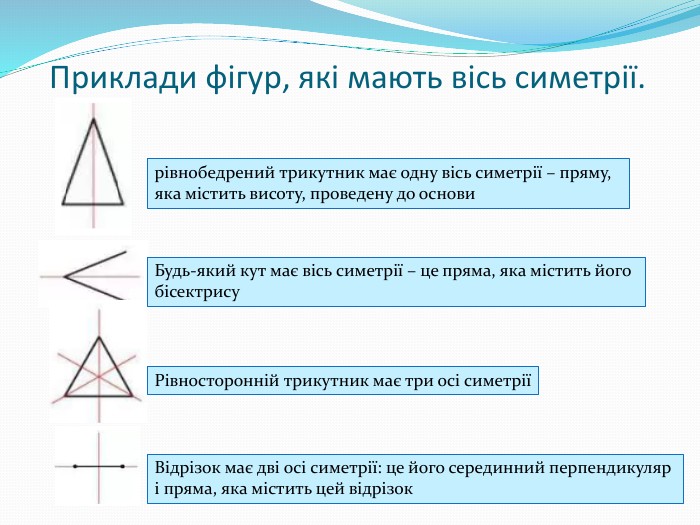
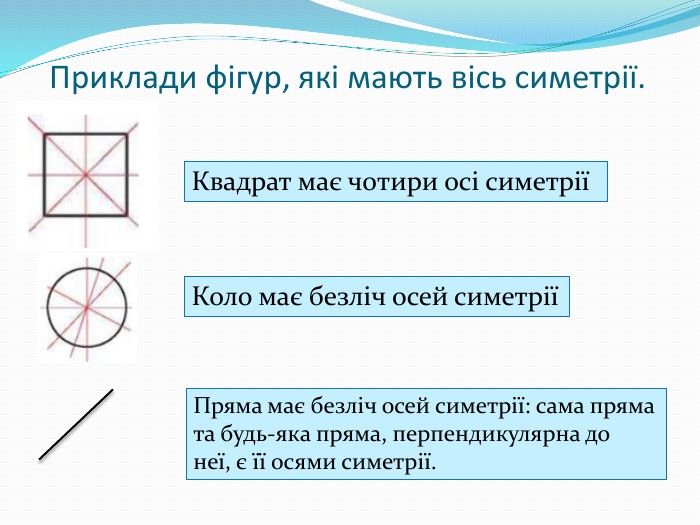
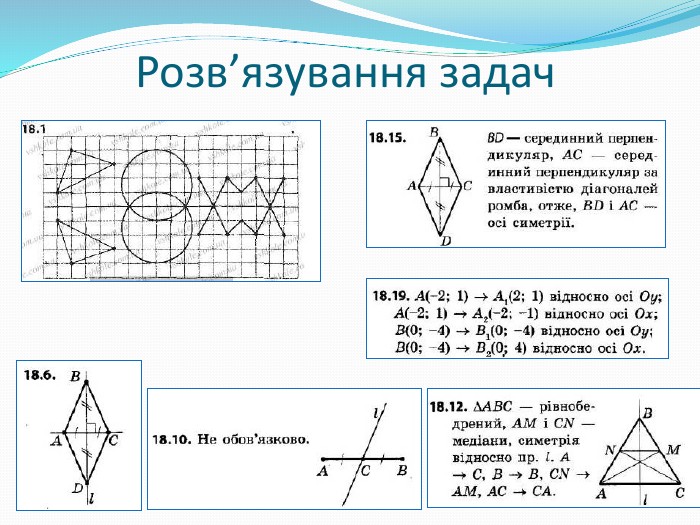
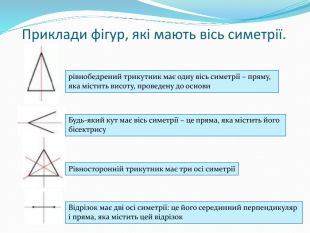
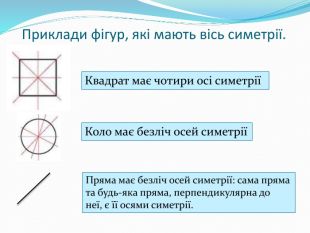
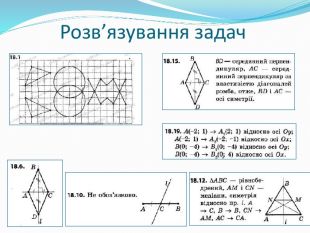
Подання нового матеріалу: введення поняття симетричних точок відносно прямої, властивостей осьової симетрії, наведення прикладів фігур, які мають осі симетрії; розв'язування задач, які передбачають використання нових понять та властивостей; здійснення зворотнього зв'язку. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
До підручника
Геометрія 9 клас (Мерзляк А. Г., Полонський В. Б., Якір М. С)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку