ГЕОМЕТРІЯ 11 клас

Контрольна робота №1
Многогранники

Варіант 1

 

1. Укажіть рисунок, на якому зображено піраміду.

 

А	Б	В	Г

2. Рівнобедрені трикутники АВС і АВD зі спільною основою АВ та висотами СО та DО утворюють двогранний кут з ребром АВ. Укажіть лінійний кут цього двогранного кута.

 

 

А	Б	В	Г
DAC	DOC	DBC	DOA

 

3. Знайдіть кількість граней семикутної призми.

 

А	Б	В	Г
7	8	9	10

 

4. На рисунку зображено пряму трикутну призму. Укажіть правильне твердження.

А Основи призми — прямокутники.

Б Бічні грані призми — трикутники.

В Висота призми дорівнює довжині бічного ребра.

Г Довжини ребер основи призми та бічних ребер однакові.

Д Одна з бічних граней призми — трапеція.

 

5. У шестикутній призмі всі бічні грані рівні й площа кожної з них дорівнює 12 см². Визначте площу всіх бічних граней призми.

 

А	Б	В	Г
2 см2	12 см2	24 см2	72 см2

 

6. Знайдіть діагональ куба, площа поверхні якого дорівнює 96 см².

 

А	Б	В	Г
см	4 см	см	см

 

7. Виміри прямокутного паралелепіпеда дорівнюють 2 см, 3 см і 1 см. Установіть відповідність між між завданнями (1–3) та числовими значеннями відповідей (А–Г) до них.

 

1	Знайдіть суму довжин усіх ребер прямокутного паралелепіпеда.	А	6
2	Знайдіть довжину діагоналі прямокутного паралелепіпеда.	Б
3	Знайдіть площу повної поверхні прямокутного паралелепіпеда.	В	22
		Г	24

 

8. Знайдіть площу бічної поверхні правильної трикутної піраміди, у якої плоский кут при вершині дорівнює 90°, а бічне ребро — 10 см.

 

9. Основою похилого паралелепіпеда є ромб, сторона якого дорівнює 60 см. Площина діагонального перерізу, що проходить через більшу діагональ основи, перпендикулярна до площини основи. Площа цього перерізу дорівнює 72 дм². Знайдіть меншу діагональ основи, якщо бічне ребро паралелепіпеда дорівнює 80 см і утворює з пло­щиною основи кут 60°.

 

10. Кажуть, що піраміди, подібні до піраміди Хеопса, позитивно впливають на людину. Піраміда Хеопса є правильною чотирикутною пірамідою. Сторона основи якої  ≈ 230 м, висота піраміди ≈ 147 м. Кут при вершині бічної грані – прямий.

1) Знайдіть для пірамід, подібних до піраміди Хеопса, відношення довжин сторони бічного ребра і основи. Відповідь дати з точністю до десятих.

2) Скільки вапняних блоків шириною 2,875 м та довжиною 4 м знадобиться для облицювання поверхні піраміди?

Варіант 2

 

1.     На якому з рисунків зображено п’ятикутну піраміду?

 

А	Б	В	Г

 

2. Кут ВАC — лінійний кут двогранного кута з ребром а, що зображений на рисунку. Оберіть правильне твердження.

 

 

А	Б	В	Г
a||b	ABa	ABb	ACc

 

3. Знайдіть кількість ребер у шестикутної  піраміди.

 

А	Б	В	Г
18	6	7	12

 

4. На рисунку зображено правильну чотирикутну призму. Укажіть правильне твердження.

 

А Основи призми — квадрати.

Б Бічні грані призми — трикутники.

В Висота призми дорівнює довжині ребра основи.

Г Довжини ребер основи призми та бічних ребер однакові.

Д. Одна з бічних граней призми — квадрат.

 

5. У п’ятикутній призмі площа основи дорівнює 5 см², а площа її бічних граней — 10 см². Знайдіть площу всіх граней призми.

 

А	Б	В	Г
15 см2	30 см2	25 см2	20 см2

 

6. У трикутної піраміди всі ребра рівні по 6 см. Знайдіть площу поверхні піраміди.

 

А	Б	В	Г
см2	см2	см2	см2

 

7. Ребро куба дорівнює 4 см. Установіть відповідність між завданнями (1–3) та числовими значеннями відповідей (А–Г) до них.

 

1	Знайдіть суму довжин усіх ребер куба.	А
2	Знайдіть довжину діагоналі куба.	Б	24
3	Знайдіть площу повної поверхні куба.	В	48
		Г	96

 

8. Знайдіть висоту правильної трикутної піраміди, сторона основи якої дорівнює  см,  а апофема — 5 см.

 

9. Основою похилого паралелепіпеда є ромб, менша діагональ якого до­рівнює 60 см. Площа діагонального перерізу, що проходить через біль­шу діагональ і перпендикулярно до площини основи, дорівнює 72 дм². Знайдіть сторону основи паралелепіпеда, якщо бічне ребро його дорів­нює 80 см і нахилене до площини основи під кутом 60°.

 

10. При виконанні ремонтних робіт кімнати, довжина якої 5,5 м, ширина 3,3 м, а висота 3,5 м, замінили шпалери. Відомо, що в кімнаті є два вікна розмірами 2,2 м х 1,5 м та двері 0,9 м х 2,1 м.

 

1) Скільки рулонів потрібно для оклеювання кімнати шпалерами, якщо ширина десятиметрового рулону 0,53 м. Врахувати, що при оклеюванні шпалер треба брати з 15% запасом?

 

2) Яку суму грошей треба мати, щоб купити шпалери, якщо 1 м² шпалер коштує 40 грн?

КОНТРОЛЬНА РОБОТА №2
Тіла обертання

Варіант 1

 

1. Серед запропонованих фігур оберіть ту, за допомогою обертання якої може утворитися циліндр.

 

 

А	Б	В	Г
ромб	прямокутний трикутник	прямокутник	трапеція

 

2.     Укажіть фігуру, яка є осьовим перерізом конуса.

 

А	Б	В	Г
круг	коло	прямокутний трикутник	рівнобедрений трикутник

 

3.     Назвіть відрізок, який сполучає дві точки сфери й не проходить через її центр.

 

А	Б	В	Г
вісь	хорда	Діаметр	дотична

 

4. Укажіть фігуру, яка є осьовим перерізом зрізаного конуса.

 

А	Б	В	Г
трикутник	паралелограм	Трапеція	круг

 

5.     Знайдіть площу осьового перерізу циліндра, твірна якого дорівнює 5 см, а діаметр основи 8 см.

 

А	Б	В	Г
40 см2	80 см2	25π см2	64π см2

 

6. Знайдіть площу великого круга кулі, якщо її радіус дорівнює 8 см.

 

А	Б	В	Г
32π см2	256π см2	16π см2	64π см2

 

7.  Дано конус, висота якого дорівнює 14 см, а кут при вершині осьового перерізу — 120°. Установіть відповідність між елементами конуса (1–3) та їх числовими значеннями (А–Г).

 

1	Радіус основи конуса.	А	28 см
2	Твірна конуса.	Б	см
3	Діаметр основи конуса.	В	см
		Г	14 см

 

8. Перерізом циліндра площиною, паралельною до його осі, є квадрат, що відтинає від кола основи дугу 90°. Знайдіть висоту циліндра, якщо від­стань від осі циліндра до цього перерізу дорівнює 5 см.

 

9. Вершини рівностороннього трикутника зі стороною  см лежать на поверхні кулі радіуса 5 см. Знайдіть відстань від центра кулі до площини трикутника.

 

10. З листа заліза, що має квадратну форму з площею 20,25 дм², отримали циліндричну трубу. При зварюванні труби краї один на другий не накладали.

 

1) Знайдіть діаметр труби, що утворилася в результаті зварювання країв залізного листа. Відповідь подати в см. Прийняти π ≈ 3.

 

2) Скільки фарби потрібно для двошарового покриття труби, якщо на 1 м² поверхні витрачається 200 г фарби?

Варіант 2

1. Серед запропонованих фігур оберіть ту, за допомогою обертання якої може утворитися конус.

 

 

 

А	Б	В	Г
ромб	прямокутний трикутник	Кут	трапеція

 

2. Укажіть фігуру, яка є перерізом кулі.

 

А	Б	В	Г
коло	півкруг	Еліпс	круг

 

3.     Назвіть відрізок, який сполучає дві точки основи циліндра й не проходить через її центр.

 

А	Б	В	Г
радіус	твірна	Діаметр	хорда

 

4. Укажіть фігуру, яка є осьовим перерізом циліндра.

 

А	Б	В	Г
прямокутник	трикутник	Трапеція	круг

 

5. Знайдіть висоту конуса, твірна якого дорівнює 10 см, а діаметр основи 8 см.

 

А	Б	В	Г
см	6 см	см	см

 

6. Знайдіть площу великого круга кулі, якщо її радіус дорівнює 4 см.

 

А	Б	В	Г
8π см2	16π см2	32π см2	64π см2

 

7.  У зрізаному конусі радіуси основ дорівнюють 2,5 см та 5,5 см. Твірна конуса нахилена до площини основи під кутом 60⁰. Установіть відповідність між елементами конуса (1–3) та їх числовими значеннями (А–Г).

 

1	Різниця діаметрів основ конуса.	А	см
2	Твірна конуса.	Б	см
3	Висота конуса.	В	3 см
		Г	6 см

 

8. У циліндрі проведено паралельно осі площину, яка відтинає від кола основи хорду, яку видно з центра цієї основи під кутом 120⁰. Висота циліндра дорівнює 10см. Знайдіть площу перерізу, якщо січна площина віддалена від осі на см.

 

9. Вершини рівностороннього трикутника зі стороною  см лежать на поверхні кулі. Знайдіть радіус кулі, якщо відстань від центра кулі до площини трикутника дорівнює 6 см.

 

 10. З тканини, що має форму квадрата площею 576 дм², вирізали круг найбільшого розміру. В центрі цього круга вирізали отвір, радіус якого дорівнює 80 см. З утвореного кільця тканини виготовили абажури для ламп, що мають форму зрізаного конуса. Діаметр нижньої частини абажура дорівнює 6 дм. Втратами на зшивання частин абажура знехтувати.

 

1) Знайдіть висоту абажура. Відповідь подати в см, попередньо округливши результат до цілих. Прийняти π ≈ 3.

 

2) Скільки абажурів виготовили з даного шматка тканини?

КОНТРОЛЬНА РОБОТА №3
Об’єми геометричних тіл

Варіант 1

 

1.     Знайдіть об’єм куба, довжина ребра якого дорівнює 4 см.

 

А	Б	В	Г
16 см3	64 см3	24 см3	8 см3

 

2. Обчисліть об’єм циліндра, осьовим перерізом якого є квадрат зі стороною 8 см.

 

А	Б	В	Г
64 см3	96 см3	128 см3	512 см3

 

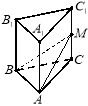3. Об’єм прямої трикутної призми ABCA₁B₁C₁ дорівнює 48 см³. Точка М — середина ребра СС₁. Обчисліть об’єм піраміди МАВС.

 

А	Б	В	Г
6 см3	16 см3	12 см3	8 см3

 

4. Обчисліть об’єм конуса, висота якого дорівнює 4 см, а діаметр основи — 6 см.

 

А	Б	В	Г
48 см3	16 см3	36 см3	12 см3

 

5.     Площа сфери 36π см². Знайдіть об’єм кулі, яку обмежує дана сфера.

 

А	Б	В	Г
36π см3	48π см3	9π см3	π см3

 

6.     Сторони основ правильної чотирикутної призми збільшили в 2 рази, а висоту зменшили в 2 рази. Установіть відношення об'єму одержаної піраміди до об'єму даної .

 

А	Б	В	Г
4 :1	2 :1	1: 2	1: 4

 

7.     Установіть відповідність між геометричними тілами (1–3) та формулами (А–Г) для обчислення їх об’ємів.

 

1	Призма	А
2	Піраміда	Б
3	Куля	В
		Г

 

8. У правильній трикутній піраміді бічне ребро дорівнює  см й утворює із площиною основи кут 45°. Знайдіть об’єм піраміди.

 

9. На рисунку зображено дві проекції деталі (вигляд спереду та зверху). Розміри подано в міліметрах. Знайдіть об'єм деталі (в мм³).

 

10. На пришкільному майданчику вирішили оформити клумби, які мають форму кульового сегмента з радіусом основи 3 м і висотою 50 см.

 

1) Скільки кубометрів землі потрібно завезти до садової ділянки для створення чотирьох таких клумб?

 

2) Яку площу повинна мати прямокутна ділянка землі на якій можна буде розмістити такі клумби, якщо відстані між сусідніми клумбами дорівнюють діаметрам клумб і клумби розміщені по кутам такої ділянки?

Варіант 2

 

1. Знайдіть об’єм прямокутного паралелепіпеда, виміри якого дорівнюють 2 см, 3 см і 5 см.

 

А	Б	В	Г
20 см3	60 см3	62 см3	30 см3

 

2. Площа основи піраміди дорівнює 24 дм², а її висота — 4 дм. Знайдіть об’єм призми.

 

А	Б	В	Г
32 дм3	64 дм3	96 дм3	48 дм3

 

3. Об’єм циліндра дорівнює 24 см³, точка М — середина осі ОО₁. Знайдіть об’єм конуса, висота якого становить МО.

 

А	Б	В	Г
6 см3	12 см3	8 см3	4 см3

 

4. Обчисліть об’єм конуса, висота якого дорівнює 6 см, а діаметр основи — 4 см.

 

А	Б	В	Г
8 см3	24 см3	12 см3	32 см3

 

5. Площа великого круга кулі дорівнює 36π см². Знайдіть об'єм кулі.

 

А	Б	В	Г
72π см3	288π см3	96 см3	192π см3

 

6. Визначте як зміниться об’єм правильної трикутної піраміди, якщо сторони її основи зменшили в 3 рази, а висота піраміди збільшиться втричі.

 

А	Б	В	Г
зменшиться в 9 разів	не зміниться	зменшиться в 3 рази	збільшиться в 3 рази

 

7.  Установіть відповідність між геометричними тілами (1–3) та формулами (А–Г) для обчислення їх об’ємів.

 

1	Конус	А
2	Циліндр	Б
3	Куб	В
		Г

 

8.     У правильній чотирикутній піраміді бічне ребро дорівнює  см й утворює з висотою піраміди кут 45°. Знайдіть об’єм піраміди.

 

9. Скирта сіна має форму прямої призми з п'ятикутною основою. Розміри скирти (у метрах) подано на рисунку. Знайдіть об'єм скирти.

10. Зовнішній і внутрішній діаметри кільця для колодязя відповідно 1,3м і
1,1м, а висота 90 см.

 

1) Скільки кубометрів бетону потрібно для виго­товлення 8 таких кілець?

 

2) Яка маса необхідного бетону, якщо його густина 1800 кг/м³. Відповідь подати в тоннах, попередньо округливши результат до цілих.

Контрольна робота №4
Площі поверхонь геометричних тіл

Варіант 1

 

1. Знайдіть площу бічної поверхні правильної трикутної піраміди у якої площа бічної грані дорівнює 4 см².

 

 

 

А	Б	В	Г
8 см2	12 см2	16 см2	64 см2

 

2. Радіус сфери дорівнює 3 дм. Знайдіть площу сфери.

 

А	Б	В	Г
4 · 3 дм2	 · 32 дм2	2 · 32 дм2	4 · 32 дм2

 

3. Знайдіть площу повної поверхні циліндра, якщо площа бічної поверхні циліндра дорівнює 10 см², а площа основи — 6 см².

 

 

 

А	Б	В	Г
16 см2	26 см2	22 см2	60 см2

 

4. Знайдіть площу бічної поверхні конуса, твірна якого дорівнює 8 см, а діаметр основи 6 см.

 

А	Б	В	Г
24π см2	48π см2	96π см2	π см2

 

5. Установіть, як зміниться площа бічної поверхні правильної чотирикутної піраміди, якщо сторону основи і висоту піраміди збільшити у 2 рази.

 

А	Б	В	Г
Збільшиться в рази.	Збільшиться в 2 рази.	Збільшиться в 4 рази.	Збільшиться в 10 разів.

 

6. Знайдіть площу поверхні тетраедра, кожне ребро якого 2 см.

 

А	Б	В	Г
см2	2 см2	4 см2	4 см2

 

7. Установіть відповідність між геометричними тілами (1–3) та формулами (А–Г) для обчислення площ їх бічних поверхонь.

 

1	Пряма призма.	А
2	Правильна піраміда.	Б
3	Конус.	В
		Г

 

8. Основою прямої призми є ромб з тупим кутом 150°. Площа бічної поверхні призми дорівнює 96 см², а площа її повної поверхні — 132 см². Знайдіть висоту призми.

9.          Знайдіть бічну поверхню зрізаного конуса, твірна якого нахилена до площини основи під кутом 30°, а площа круга, вписаного в його осьовий переріз, дорівнює 4 см².

 

 

10.     Для виготовлення повітряної кулі радіусом 2 м обирають тканину завширшки 90 см. При цьому на шви та відходи витрачається 10% матерії.

 

1.          Скільки метрів матерії потрібно купити для пошиття повітряної кулі? Відповідь представити цілим числом.

 

2.          Яка маса повітря, що міститься в такій кулі, якщо густина повітря ρ = 1,225 кг/м³. Відповідь представити цілим числом.

 

Варіант 2

 

1. Знайдіть площу бічної поверхні правильної чотирикутної призми у якої площа бічної грані дорівнює 3 см².

 

А	Б	В	Г
18 см2	27 см2	12 см2	9 см2

 

2.     Радіус кулі дорівнює 5 дм. Знайдіть площу поверхні кулі.

 

А	Б	В	Г
4 · 5 дм2	 · 52 дм2	2 · 52 дм2	4 · 52 дм2

 

3. Знайдіть площу повної поверхні конуса, якщо площа бічної поверхні конуса дорівнює 10 см², а площа основи — 7 см².

 

 

А	Б	В	Г
17 см2	24 см2	27 см2	70 см2

 

4. Площа бічної поверхні куба 36 см². Знайдіть пло­щу повної поверхні куба.

А	Б	В	Г
54 см2	42 см2	48 см2	60 см2

 

5 Установіть, як зміниться площа бічної поверхні правильної трикутної піраміди, якщо сторону основи і висоту піраміди зменшили у 2 рази.

 

А	Б	В	Г
Зменшиться в рази.	Зменшиться в 2 рази.	Зменшиться в 4 рази.	Зменшиться в 10 разів.

 

6. Повна поверхня  тетраедра дорівнює 2см². Знайдіть довжину ребра.

 

А	Б	В	Г
см	см	2 см	3 см

 

7. Установіть відповідність між геометричними тілами (1–3) та формулами (А–Г) для обчислення площ їх поверхонь.

 

1	Куля	А
2	Циліндр	Б
3	Куб	В
		Г

 

8. Основою прямої призми є ромб з гострим кутом 30°. Площа бічної поверхні призми дорівнює 86 см², а площа її повної поверхні — 150 см². Знайдіть висоту призми.

 

9. У зрізаному конусі висота дорівнює  см, його твірна утворює із площиною основи кут 60° і перпендикулярна до діагоналі осьового перерізу, що проходить через цю твірну. Знайдіть бічну поверхню зрізаного конуса.

 

10. При прокладанні системи опалювання міста довжиною 3 км були використані труби діаметром 60 см.

 

1. Скільки метрів листового заліза завширшки 1,9 м було використано? Втратами на зварювання знехтувати.

 

2. Визначити об’єм землі, яку треба вивезти при укладанні труб. 

Контрольна робота №5
Повторення

Варіант 1

 

1. Кут АОВ — лінійний кут двогранного кута з ребром а, що зображений на рисунку. Серед запропонованих відповідей оберіть ту, яка є правильною.

 

 

А	Б	В	Г
ОАС = 90°	АОС = 90°	АСВ = 90°	АВО = 90°

 

2.     Знайдіть довжину відрізка АВ, якщо А(–6; 0; 0) і В(3; 0; 0).

 

А	Б	В	Г
81	9	3

 

3.     Укажіть кількість ребер у п’ятикутної призми.

 

А	Б	В	Г
10	5	7	15

 

4. Знайдіть висоту МО правильної чотирикутної піраміди, якщо апофема МК  дорівнює 17 см, а її проекція на площину основи дорівнює 15 см.

 

А	Б	В	Г
8 см	32 см	7 см	12 см

 

5. У кулі з центром О проведено переріз із центром О₁ на відстані 5 см від центра кулі. Знайдіть радіус перерізу, якщо радіус кулі дорівнює 13 см.

 

А	Б	В	Г
4 см	6 см	8 см	см

 

6. Знайдіть довжину вектора  , якщо (1; –3; 3) і (2; –1; 2).

 

А	Б	В	Г
7		5

 

7. Дано циліндр, діагональ осьового перерізу якого дорівнює l й утворює із площиною основи кут . Установіть відповідність між геометричними величинами (1–3) та формулами (А–Г) для їх обчислення.

 

1	Площа осьового перерізу циліндра.	А	l3cos2sin
2	Об’єм циліндра.	Б	l2cossin
3	Площа бічної поверхні циліндра.	В	l2cossin
		Г	l2cossin

 

8. У правильній трикутній піраміді бічна грань утворює із площиною основи кут 60°. Визначте площу бічної поверхні піраміди, якщо радіус кола, описаного навколо її основи, дорівнює  см.

 

9. Основа конуса вписана в основу правильної трикутної призми. Вершина конуса належить іншій основі призми. Знайдіть об’єм конуса, якщо площа бічної поверхні призми дорівнює дм², а її висота — 10 дм.

 

10. Флакон чоловічої туалетної води «Кензо» має форму прямокутного паралелепіпеда з розмірами: довжина – 4см, висота – 8 см, ширина – 1,5 см. Чоловік витрачає 1 см³ туалетної води за 3 дні.

 

1) Скільки днів ми зможемо насолоджуватися запахом цього парфуму з такого флакона?

 

2) Скільки флаконів туалетної води можна перевезти в контейнері розміри якого 32 см х 30 см х 60 см?

Варіант 2

 

1. Кут ВАC — лінійний кут двогранного кута з ребром а, що зображений на рисунку. Серед запропонованих відповідей оберіть ту, яка є правильною.

 

А	Б	В	Г
a||b	ABa	ABb	ACc

 

2.     Знайдіть координати середини відрізка MN, де M(–4; 3; 9) і N(2; –1; –5).

 

А	Б	В	Г
(1; –1; –2)	(6; –4; –14)	(–3; 2; 7)	(–1; 1; 2)

 

3.     Укажіть кількість ребер у п’ятикутної піраміди.

 

А	Б	В	Г
10	6	15	5

 

4. Основою піраміди МАВСD є квадрат зі стороною 6 см. Бічне ребро MB перпендикулярне до площини основи піраміди, МВ = 8 см. Точка K — середина ребра CD. Знайдіть відстань від точки М до СD.

 

 

А	Б	В	Г
см	см	10 см	см

 

5. У кулі з центром О проведено переріз із центром О₁ на відстані 12 см від центра кулі. Знайдіть радіус кулі, якщо радіус перерізу дорівнює 9 см.

 

 

А	Б	В	Г
10 см	15 см	12 см	21 см

 

6 . Знайдіть довжину вектора , якщо (–1; –2; 2) і (2; 2; –2).

 

А	Б	В	Г
3	5

 

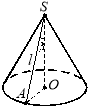7. Дано конус, твірна якого дорівнює l й утворює з висотою кут . Установіть відповідність між геометричними величинами (1–3) та формулами (А–Г) для їх обчислення.

 

1	Площа основи конуса.	А	l3sin2cos
2	Площа повної поверхні конуса.	Б	l2sin2
3	Об’єм конуса.	В	l2cossin
		Г	l2sin(1 + sin)

 

8. У правильній чотирикутній піраміді бічна грань утворює із площиною основи кут 60°. Визначте площу бічної поверхні піраміди, якщо радіус кола, вписаного в її основу, дорівнює 4 см.

 

9. У циліндр вписано правильну чотирикутну призму, площа бічної поверхні якої дорівнює дм². Довжина бічного ребра призми  - 7 дм. Знайдіть об’єм циліндра.

 

10. Для опалювальної системи будинку необхідні радіатори з розрахунку: три одиниці на 50 м³. Будинок має довжину 30 м, ширину 20 м і висоту 15 м.

 

1) Скільки радіаторів треба замовити на новий будинок?

 

2) Скільки метрів утеплювального матеріалу (висотою 3 м) потрібно, щоб «зашити» стіни будинку, якщо площа стін становить 80% бічної поверхні будинку.

ВИКОРИСТАНІ ДЖЕРЕЛА

 

1.     Бевз Г.П., Бевз В.Г., Владімірова Н.Г., Владіміров В.М. Геометрія. 11 клас. Академічний та профільний рівень.
2.     Комплексний зошит для контролю знань. Геометрія. 11 клас. О. М. Роганін. -  Х.: Видавництво «Ранок», 2011.
3.     Збірник завдань для державної підсумкової атестації з математики.11 клас: У 2 кн. Кн.1/ М.І.Бурда, О.Я. Біляніна, О.П. Вашуленко та ін.- Х.: Гімназія, 2008.
4.     М.Л.Крайзман . Розв’язування геометричних задач методом векторів. Київ., 1980.
5.     А.П.Єршов, В.В.Голобородько. Геометрія 10-11кл. Харків « Гімназія» , 2002.
6.     В.О.Швець, Ф.Г.Деркач. Дидактичні матеріали з математики. 11 кл. Київ. «Освіта» ., 1997.
7.     А.М.Капіносов. Геометрія 11 клас. Дидактичні матеріали для різнорівневого навчання. Дніпропетровськ.,1993.
8.     О.М.Афанасьєва, Я.С.Бродський. Геометрія 10- 11кл. Тернопіль., 2003.
9.     Л.Кондратьєва. Дидактичні матеріали для тематичного оцінювання з геометрії. Тернопіль « Підручники & посібники» ., 2002.
10. А.Г.Мерзляк. В.Б.Полонський. Збірник задач і завдань для тематичного оцінювання . Геометрія 11 клас. Харків. « Гімназія» 2007.