Науково дослідницька робота про хокей

Міністерство освіти і науки України

департамент освіти і науки

Сокальська Мала академія наук учнівської молоді

 

 

Відділення: математика

Секція: математичне модеьвання

 

 

МАТЕМАТИЧНЕ МОДЕЛЮВАННЯ В ХОКЕЇ

 

 

 

 

Роботу виконав:

Грицишин Віталій Олегович

учень 10 класу

Сокальського ліцею № 3,

слухач Малої академії наук

 

Науковий керівник:

Кровіцька Лариса Ярослаівна

вчитель математики Сокальської

Малої академії наук

                                                                                                  учнівської молоді

 

 

 

 

 

ЗМІСТ

ВСТУП……………………………………………………………………………..3

РОЗДІЛ 1 ТЕОРЕТИЧНІ ОСНОВИ ПРОБЛЕМИ ДОСЛІДЖЕННЯ

1.1.Поява хокею в Україні…………………………………………………5

1.2.Математика і спорт ……………………………………………………6

РОЗДІЛ 2 МАТЕМАТИЧНІ МОДЕЛІ В СПОРТІ

2.1. Аспекти сучасного математичного моделювання в спорті………………………………………………………………………………8

2.2. Математичні й геометричні закономірності в хокеї……………….10

2.3. Задача про призначення……………………………………………...11

РОЗДІЛ 3 ЗАДАЧІ ПРИКЛАДНОЇ МАТЕМАТИКИ В ХОКЕЇ

 3.1. Хокейна команда «Білий Барс»……………………………………...13

 3.2. Закон розподілу кількості шайб у матчі…………………………….13

ВИСНОВКИ…………………………………………………………………...…21

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ…………………..………………...…22

 

 

 

 

 

 

 

 

 

 

 

ВСТУП

За останні роки багато  фахівців у сфері спортивної науки — тренерів, лікарів, фізіо­логів, біохіміків, біомеханіків, психологів — почали усвідомлювати те, що математичні методи, зокрема математичне моделювання, — це унікальний і по­тужний інструмент дослідження організму людини в процесі адаптації до тренувальних навантажень, інструмент аналізу тренувального процесу та про­гнозування спортивного результату. У сучасній спортивній науці є яскраві приклади використання математичних методів для розв’язання різних задач, побудованих як на аналітичних, так і стохастичних моделях. Цю характерну тенденцію сучасного етапу розвитку наукових досліджень у галузі фізичної культури та спорту відображено в переліку основних завдань провідних наукових товариств, які працюють у цій сфері: ISBS (International Society ofBiomechanics in Sports), IACSS (International Association of Computer Science in Sport), IASI (International Association for Sports Information), ISEA (International Sports Engineering Association). Також щорічно проводяться міжнародні конференції,- серед яких одна з найбільш помітних — MathSport International Conference.

Метод моделювання як метод наукового нізнання становить відтворення форми чи деяких властивостей предметів або явищ із метою їх вивчення. Матема­тична модель допомагає вибудувати план .тренувань і належним чином коригувати тренувальний процес, що виводить спортсмена на пік спортивної форми, мі­німізуючи «фізіологічну ціну» спортивного результату.

Мета дослідження: з’ясувати закономірності ма­тематичного- моделювання в хокеї та проаналізувати функціонування утворених моделей.

Предмет дослідження: розподіл спортивних амплуа гравців та ймовірна кількість шайб, які може забити хокейна команда у домашньому та гостьових  матчах.

Об’єкт дослідження: математичні моделі з еле­ментами лінійної алгебри й теорії ймовірностей.

Завдання дослідження :

 1Опрацювати теоретико-методологічні джерела щодо теми дослідження;

 2.Створити  математичну модель  розподілу спортивних амплуа гравців, щоб загальна результа­тивність дій усієї команди виявилася найбільшою;

 3.Підрахувати ймовірну кількість шайб і побу­дувати графік розподілу забитих шайб .хокейною командою у домашньому та гостьових матчах.

Серед методів дослідження, які було використанно в процесі роботи, можна виділити такі:

теоретичний — вивчення та аналіз відповідних інформаційних джерел;

практичний — систематизація й узагальнення теоретичного матеріалу, методи математичної ста­тистики, створення математичних моделей.

Актуальність. Хокей — це один із найпопулярніших видів спорту на нашій планеті. Необхідність вирішувати, як діяти у грі в хокей, виникає в бага­тьох спортивних ситуаціях: організації тренувань та змагань, комплектуванні спортивних команд, розподілі спортивних амплуа гравців, виборі так­тики гри тощо. Дослідження операцій є своєрід­ною  математичною  «репетицією » майбутніх рішень, що дають можливість економити час, сили й матеріальні засоби, уникати серйозних помилок, на яких уже не можна вчитися. Що дорожчий, масштабніший плановіший захід, то менше допустимі в ньому «помилкові  рішення» й важливішими стають наукові методи, що дають можливість заздалегідь оцінити наслідки кожної  гри, попередньо відкинувши неприпустимі варі­анти й рекомендувати найбільш вдалі. Застосування математичних методів і математичного моделювання сприяє організації більш ефективної роботи тренер­ського складу й команди.

Практичне значення. Науково-дослідна робо­та дає можливість розширити межі застосування математичного моделювання в хокеї та збагачує вміння й навички розв'язування задач із теорії ймовірностей.

 

 

РОЗДІЛ 1

ТЕОРЕТИЧНІ ОСНОВИ, ПРОБЛЕМИ ДОСЛІДЖЕННЯ

1.1.Поява хокею в Україні

Історія хокею з шайбою є однією з найбільш су­перечливих серед усіх видів спорту. Назва «хокей», імовірно, походить від старофранцузького hoguet, що означає «пастуша палиця з крюком». Уперше слово «хокей» згадано в Англії в 1799 році. Але са­ма гра з’явилася набагато раніше. Відомо, що грою з посохом і м’ячем захоплювалися в Стародавньому Єгипті та Стародавній Греції. Розважалися схожим чином японці й ацтеки, лише замість шайби вико­ристовували м’ячі й невеликі камені. Дуже поширена версія, що місцем винаходу хокею з шайбою є північ Канади, а придумали гру нібито солдати, які розва­жалися тим, що палицями ганяли по льоду замерзлих озер порожні консервні банки. Ці банки й стали про­образом плоскої гумової шайби. Офіційно ж історія хокею з шайбою почалася в Канаді. Саме тут уперше були чітко визначені його правила.

Хокей із шайбою має в Україні свою історію. Честь проведення першого хокейного матчу випала Львівському товариству їзди на ковзанах, заснова­ному в 1860 роках у Львові. У жовтні 1904 року було вирішено організувати хокейні змагання у Львові, 16 січня 1905 року було проведено хокейний матч за участю львівського клубу «Чарні». У січні 1909 ро­ку на ковзанці Львівського товариства Лижнярського було проведено хокейний матч за всіма міжнародними правилами. А в 1910 році в спортивному журналі «Ві­сті з Запорожа» були надруковані правила канадського гокею (гаківки), тобто хокею українською мовою.

У 1911 році Львівська газета «Діло» писали про тс, що піонер українського спортивного руху професор Іван Боберський намагався впровадити поний вид спорту — гаківку.

 

У тому ж році створено спортивне Товариство студентів вищих шкіл «Україна», а в 1912р. — було створено секцію хокею при тонаристаї «України» за сприяння голови Романа Сизика й орітніїзоаапо першу в Україні хокейну команду «СТ України» (ідеться про хокей із шайбою — канадський хокей). Хокейна дружина брала участь у чемпіонаті Польщі. Хокейний клуб існував із 1929 по 1943 рік.

На тій частині території України, що входила до складу Російської імперії, хокей уперше з’явився в 1912 році в Харкові. У нього грали спортсмени спор­тивних клубів «Гельферіх Саду» і «Фенікс». Проте хокей великої популярності не набув і незабаром ним перестали цікавитися.

Нині хокей в Україні є одним із найпопулярніших видів спорту. Про високий рівень підготовки українських хокеїстів свідчать їхні досягнення на міжнародному рівні. Так, відповідно до рейтингу Міжнародної федерації хокею (МФХ) Україна посідає 19-те місце серед 48 команд у світовому рейтингу.

1.2. Математика і спорт

Багато спортивних ситуацій доцільно роз­глядати, аналізувати й оцінювати з математичних позицій. Деякі з таких ситуацій, що піддаються вивченню методами прикладної мате­матики я досліджував з  книжи  «Математика і   спорт».

Виклад ведеться на двох рівнях. На одному — в описовій формі наведені формулювання завдань і вказані методи їх розв’я­зання, на іншому — побудовані математичні моделі, розглянуто математичний апарат.

Застосування методів матема­тичної стохастики в спортивних іграх зазвичай обмежується вка­зуванням кількості набраних очок, перемог, нічиїх, поразок, різницею забитих і пропущених шайб. Біль­шість досліджень присвячено порів­нянню результатів окремих команд або першостей, але не проаналізовано сукупні результати всіх команд або гравців за їх спортивним амплуа. Автори статті «Математическая статистика в ко­мандних видах спорту» розглядають та аналізують результати хокейного сезону, використовуючи коефі­цієнт  кореляції для знаходження ступеня залежності тих чи інших показників хокейних команд або гравців за підсумками чемпіонату.

Сфера застосування математичних методів у спорті весь час розширюється. Під час вибору раціональних варіантів атакуючих і оборонних дій, ефективних засобів і методів підготовки гравців спортивних команд дуже корисною може виявитися інформація, отримана в результаті статистичного аналізу за­гальної діяльності гравців і команди загалом. У праці «Математико-статистические методи в спорте» автори доводять, що виявлення статистично значущих законо­мірностей гри дає можливість використовувати отримані об’єк­тивні дані під час планування тренувальних навантажень.

Для моделювання спортивної гри, прогнозування  результатів  матчу  двох  команд і створення  букмекерської лінії  можна  використовувати  методи  математичної  статистики й  випадкові  величини.

 

 

 

 

 

 

РОЗДІЛ 2

МАТЕМАТИЧНІ МОДЕЛІ В СПОРТІ

2.1. Аспекти сучасного математичного моделювання в спорті

Моделювання в спорті допомагає вирішувати ши­роке коло питань: система вимірювання параметрів, задачі про харчовий раціон спортсменів різних видів спорту, формування  команди для змішаної естафети та в ігрових командних видах спорту, питання спор­тивного суддівства, прогнозування результативності змагань, прийняття рішень в умовах невизначеності під час гри тощо.

Математичними моделями, мета яких обгрун­тувати прийняття в даній ситуації того чи іншого з можливих рішень, займається найважливіший розділ прикладної математики — дослідження операцій. Не так уже й часто в результаті вивчення математичної моделі вдається дійти однозначного рішення — знайти єдине оптимальне рішення. У більшості випадків удається лише звузити коло пошуку оптимальних розв’язків (яких може бути кілька), прийняти рішення, наближені до оптимальних. Однак і це варте того, щоб вдатися до подібних розрахунків. Розгляньмо декілька практичних завдань, які може бути розглянуто за допомогою методів теорії дослі­дження операцій.

1. Розподіл  ігрових амплуа в спортивній команді, а саме  в футбольній, хокейній тощо, що забезпечує найбільший ефект у грі.
2. Система організації чемпіонатів. турнірів, і кубкових зустрічей, що забезпечує досягнення певних цілей. Наприклад: виявлення першого й другого призерів кубкових зустрічей.
3. Складання для спортсменів дієти, що відповідає вимогам медиків і водночас є найбільш економною та зберігає вагу спортсмена в певних межах; розробка індивідуального . режиму тренувань.

У математичних моделях для опису фізіологічних явищ використовують дані комп’ютерного експери­менту, завдяки чому можна кількісно передбачати різні явища, що випливають із модельних уявлень. Словесний, образний опис фізіологічних явищ і наслідків, що випливають із них, не має таких можливостей. Багато вербальних висловлювань про механізми фізіологічних явищ на перший погляд можуть здаватися такими, що не суперечать одне од­ному, але не витримують критики при математичному описі.

Для моделювання спортивної гри, прогнозування результатів матчу двох команд і створення букмекерської лінії можливо використовувати методи матема­тичної статистики й випадкові величини. Зокрема, для голів футболу й хокею добре нідходить розподіл Пуассона (кількість голів) (рис. 2.1, а) та розподіл Скеллама (різниця голів) (рис. 2.1, б), для бейсболу— від’ємний біноміальний розподіл, а для гандболу й баскетболу — нормальний розподіл (кількість та різниця голів / очок) (рис. 2.1, в).

 

   

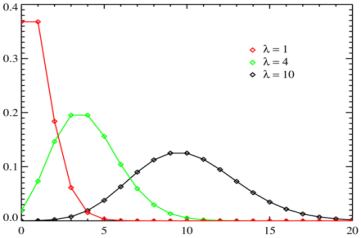
Рис. 2.1. а

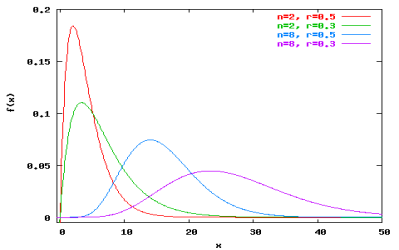
Рис. 2.1, б

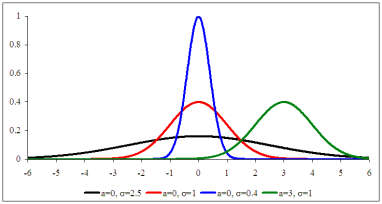
Рис. 2.1, в

Математика, особливо прикладна математика, пояснює багато послідовностей і закономірностей у спорті. За допомогою математичних моделей можуть бути вирішені практичні завдання в спорті, що допоможе спортсменам і тренерам досягти найвищих результатів. Наприклад, український тренер Борис Дороженко, грунтуючись на знаннях із математики, створив свою систему занять і став справжньою знаменитістю в США, зігравши клю­чову роль у становленні нової зірки світового хокею Остонена Меттьюса.

Майданчик для гри в хокей із шайбою повинен бу­ти оточений пластиковими або дерев'яними бортами заввишки не менше ніж 1,17 м і не більше ніж 1,22 м над рівнем поверхні льоду.

2.2.  Математичні  і геометричні закономірності в хокеї

З погляду математики й геометрії, гравці на хокей­ному полі є вершинами рухомих геометричних фігур, _t що видозмінюються в процесі гри. Два гравці мають лише один варіант взаємодії — передача між собою.

Три хокеїсти утворюють форму рухомого трикутника, що постійно видозмінюєть­ся, і мають уже 14 неповто­рюваних варіантів взаємодій. У чотирьох гравців їх 62, а в повній п'ятірці — міні­мум 142! Основою комбіну­вання в грі є функціональний трикутник, що складається з трьох хокеїстів, які мають достатню кількість варіантів взаємодії для ефективної гри. Кожен наступний гра­вець, який підключається до комбінації, збільшує варіативність взаємодій, але збільшується і ймовір­ність помилок.

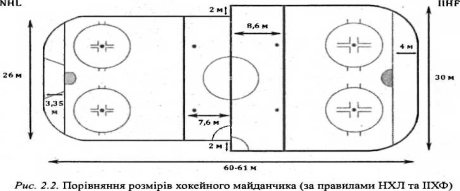Чимало цікавих математичних закономірностей пов'язано і з розмірами хокейного майданчика. У правилах Міжнародної федерації хокею з шайбою (ІІХФ) і Національної .хокейної ліги (НХЛ) розміри хокейного майданчика різняться (рис. 2.2).

 

 

 

 

 

 

За правилами ІІХФ, рекомендований розмір пло­щадки для гри в хокей із шайбою 60—61 м завдовжки і 29—ЗО м завширшки (для офіційних змагань під егі­дою ІІХФ); для інших змагань мінімальний розмір майданчика становить 56 х 26 м.

За правилами НХЛ, рекомендований розмір пло­щадки для гри в хокей із шайбою — 200 х 85 футів (60,96 х 25,90 метрів). У НХЛ вважається, що мен­ші розміри сприяють силовій боротьбі, кидкам по воротах, грі біля бортів, де відбувається багато єдиноборств, сутичок і бійок, що робить гру видо­вищнішою. А великі ж розміри майданчика' сприяють грі в пас та обережному захисному стилю.

Кути хокейного майданчика мають бути заокругле­ні дугою кола радіусом від 7 м до 8,5 м за правилами ІІХФ і 28 футів (8,53 м) в НХЛ.

2.3. Задача про призначення

Задача про призначення на вербальному рівні фор­мулюється так: розподілити між гравцями команди обов'язки (рис. 2.4) так, щоб загальна результативність дій усієї команди виявилася найбільшою. Для задачі про призначення існує зручна математична модель.

Побудуємо математичну модель про призначення в хокейній команді. У кожній іздвох команд під час гри в повному складі 5 польових гравців та воротар. Нада­мо гравцям А, В, С, D, Е, Fвідповідні номери і = 12,3, 4,5,6. Аналогічно позначимо номерами  j = 12,3,4,5,6 обов'язки центрального, лівого та правого нападників, лівого та правого захисників та воротаря, відповідно.

Введемо до розгляду 36 невідомих Ху, значення яких інтерпретуємо як вказівки про виконання обов'язків типу j. Кожна змінна Xy може набувати лише одне з можливих значень:

X_ij=

 

Сукупність невідомих величин  Ху складає матриця  призначень:

 

Х=  (1)

У кожному рядку та в кожному стовпчику матриці X лише один із елементів може дорівнювати 1, а реш­та — 0. Ця обов’язкова умова (обмеження) може бути записано у вигляді системи рівнянь 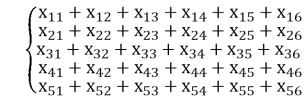                                         (2)

Також слід урахува и умову невід'ємності неві­домих х_у > 0 (і = і, 2, 3,4, 5,6 j = І, 2, 3, 4, 5,6).      (3)

Гравець під номером і, якого призначено на роль J, внесе свою долю в загальну ефективність команди F(x) у розмірі а_ij • х_ij, де а_ij — бали гравця.

Знаходження матриці призначення X, яка надасть ефективності F(x) = (4), найбільшого значення, зводиться до наступної математичної задачі: серед усіх невід’ємних розв’язків Хij > 0 (i = і, 2, 3, 4, 5.6  j = 12,3,4,5,6) системи обмежень (1) та (2) вибрати такий, що надає функції (4) найбільшого значення.

РОЗДІЛ ІІІ

ПРИКЛДНІ ЗАДАЧІ МАТЕМАТИКИ В ХОКЕЇ

1.           Хокейна команда «Білий барс»

Хокейний клуб «Білий Барс» засновано у 2008 ро­ці за ініціативи колишніх хокеїстів Віталія Федяніна та Костянтина Буценка на базі команди «Барс», яка тричі ставала срібним призером чемпіонатів України з хокею.

У вересні 2008 року команда здобула перший за свою історію трофей — «Кубок Федерації — від­криття сезону».

У подальшому команда продовжила успішні виступи вже в чемпіонаті України, за підсумками першого етапу якого посіла друге місце. У серії ж плей-оф команда зуміла здолати спочатку дніпро­петровський «Приднінровськ», потім у півфіналі в трьох поєдинках ХК «Харків», і завдяки цьому вийшла у фінал. У фіналі на команду з Броварів очікував Київський  «Сокіл». У двох вирішальних поєдинках, _що проходили в Палаці спорту, «Білий Барс» поступився досвідченішим суперникам. Так, уже в перший рік свого існування білоцерківчани зуміли вибороти срібні нагороди чемпіонату України.

7 грудня 2012 року на вулиці Молодіжній у Білій Церкві було відкрито «Льодовий стадіон», який став домашньою ареною команди «Білий Барс».

2.           Закон розподілу кількості забитих шайб у матчі

Прогнозувати матчі в хокеї досить складно, тому що жоден фаворит не може гарантувати собі перемогу в матчі. У хокеї шанси не програти значно вищі, ніж у футболі. Крім того, малюнок і характер гри часто змінюються під час матчу в разі, якщо тренерські заготовки не спрацювали

На результат матчу, крім  класу команд, впливає багато чинників:

• утома — матчі проходять через день, а якщо це виїзна серія, то перельоти й готелі банально ви­снажують гравців;
• приховані травми гравців — часто хокеїсти виходять на лід із ушкодженнями або незагоєними травмами, що робить честь їхнім людським яко­стям, але часто негативно впливає на гру. Клуби не афішують подібну інформацію. Отримати  можна при перегляді попередніх матчів, а також  відсутності гравця на тренуванні або ж його занять за індивідуальною програмою. Хокейний матч — це протистояння не лише гравців, а й тренерів, їх ігрових концепцій.

Застосовуючи закони математики й математичного моделювання, можна допомогти тренеру знайти доцільне просторове розташування гравців, схеми, за якими ефективніше діяти в тій чи іншій ігровій ситуації, і навчити цього гравців.

Розподіл кількості забитих шайб із відповідними ймовірностями визначимо як розподіл Пуассона.

Французький математик Сімеон Дені Пуассон (рис. 3.1) створив розподіл, названий на його честь, який дає можливість розподілити наявні дані по всьому спектру результатів для кожної команди.

Рис. 3.1.

Пуассонівський розподіл справедливий для подій, які мають малу ймовірність чи трапляються нечасто (наприклад, п = 1000, р = 0,002). Ним, наприклад, можна описати ймовірність того, що футболіст заб’є гол у конкретному матчі. Іноді футболіст забиває гол, рідше два, ще рідше робить хет-трик, а Пеле одного разу забив вісім. Найчастіше футболіст не забиває жодного.

Імовірність забити k голів за гру визначається параметром А, що є середньою кількістю голів, які за­биває футболіст. Якщо А велике число, то ймовірність має досягати максимуму при якомусь k. У такому разі йдеться радше про баскетболіста, який може набирати, наприклад, 22 очки за гру в середньому. Тоді ймовірність набрати 2 очки буде малою. Імовір­ність набрати 42 очки теж буде малою, а максимум імовірності буде в області саме 22 очок.

Випадкова величина X  називається  розподіленою за законом Пуассона або має пуассонівський розподіл із параметром X, якщо для неї виконується наближена рівність:

Pr (X=k), k,

де Рг(А) — імовірність того, що випадкова величина X набуде значення k Імовірність забити k шайб за гру визначається параметром    , що є середньою кількістю шайб, які забиває хокейна команда.

Припустимо, що в наступному турнірі повинні зустрггися дві команди: «Білий Барс» (господар) та лі­дер турнірної таблиці в сезоні 2016—2017 «Донбас Донецьк» (гість).

Для розрахунку результативності майбутнього матчу необхідно обчислити «силу атаки» й «силу захисту» обох команд. Дані візьму зі статистики турніру (рис. 3.2):

 

Зіграно Матчів	Перемоги господарів	Нічиї	Перемоги гостей	Голи(за матч)	Голи Господарів	Голи Гостей
180	47,8%	7,8%	44,4%	9,90	5,09	4,81
Більше 3,5	Менше 3,5	Більше 4,5	Менше 4,5	Більше 5,5	Менше 5,5	Більше 6.5
93,3%	6,7%	86,7%	13,3%	80%	20%	69,4%
Шайби Період 1	Шайби Період 2	Шайби Період 3
29,2%	35,6%	35,2%

 

Рис. 3.2. Статистика турніру 2016—2017

 

Силою атаки будемо називати відношення се­редньої кількості голів, забитих командою на своєму полі, до усіх голів, забитих командою.

Силою захисту будемо називати відношення середньої кількості голів, пропущених командою на своєму полі, до пропущених шайб усіма командами турніру.

З'ясуємо коефіцієнт сили атаки команди «Білий Барс». Cередню кількість голів, забитих командою на своєму полі, визначимо так: знайдемо відношення кількості голів, які команда забила на своєму полі, до кількості домашніх матчів. Дані візьмемо з таблиці результативності (рис. 3.3):

23 : 6 3,83 (шайби).

		I	B	BO	ПО	П	Голи
		10	5	0	0	5	44-49	4,4-4,9	-0,5
Білий барс	Дома	6	2	0	0	4	23-36	3,8-6,0	-2,2
	У гостях	4	3	0	0	1	21-13	5,2-3,2	2

 

Рис. 3.3. Результативність команди «Білий Барс»

Після цього розділимо середню кількість голів команди «Білий Барс» на середню кількість голів, узагалі забитих господарями поля: коефіцієнт сили атаки «Білого Барсу» = 3,83 : 5,09 ~ 0,75.

Аналогічно розраховуємо коефіцієнт сили атаки «Донбас Донецьк». Для цього скористаємося . даними з турнірної таблиці (рис. 3.4).

 

		І	В	ВО	ПО	П	Голи
		10	8	2	0	0	48-12	4.8-1,2	3,6
Донбас Донецьк	Дома	5	3	2	0	0	21-7	4,2-1,4	2,8
	У гостях	5	5	0	0	0	27-5	5,4-1	4.4

 

Рис. 3.4. Результативність команди «Донбас Донецьк»

Середня результативність команди складає: 27: 5 = 5,4 (шайби). Поділимо середню гостьову результативність команди «Донбас» (Донецьк) на се­редню гостьову результативність усіх команд турніру: коефіцієнт сили атаки «Донбас» (Донецьк) = = 5,4:4,81 = 1,12.

Тепер розрахуємо силу захисту в обох командах. Для цього візьмемо результативність господарів та гостей за матч і поміняємо їх місцями, тобто:

• господарі пропускали в середньому за матч 4,81 шайби;
• гості пропускали в середньому за матч 5,09 шайби.

Знайдемо силу захисту команди «Білий Барс». Для цього розділимо загальну кількість пропущених шайб за останній сезон на кількість матчів, а потім поділимо на середню кількість пропущених шайб усіма командами турніру: коефіцієнт сили захисту «Білого Барсу» = 36 : 6 : 4,81 = 1,24.

Коефіцієнт вийшов більше ніж 1, а це означає, що «Білий Барс» пропускав на 24 % шайб більше, ніж у середньому інші команди турніру.

Тепер обчислимо силу захисту «Донбас» (Донецьк): коефіцієнт сили захисту «Донбас» (Донецьк) = 5:5: 5,09 = 0,19.

Коефіцієнт вийшов менше ніж 1, а це означає, що «Донбас» (Донецьк) пропускав на 81 % менше шайб, ніж у середньому інші команди турніру.

Тепер, знаючи коефіцієнти сили атаки й захисту, можна розрахувати ймовірність для випадкової ве­личини X— кількості забитих і пропущених шайб: середня кількість шайб команди «Білии Барс» = сила атаки «Білий Барс»  сила захисту команди «Донбас» (Донецьк)  середня кількість шайб, забитих господарями поля. Маємо: середня кількість шайб «Білий Барс» = 0,75 * 0,19 * 5,09 = 0,73.

Розрахуємо затією ж формулою кількість голів, які може забити «Донбас» (Донецьк): середня кількість шайб команди «Донбас» (Донецьк) = сила атаки «Донбас» (Донецьк)  сила захисту команди «Білий Барс» середня кількість шайб, забитих гостями поля. Маємо: середня кількість шайб команди «Донбас» (Донецьк) = 1,12 * 1,24 * 4,81 = 6,68.

Звісно, матч не може закінчитися з рахунком 0,73 : 6,68. Це лише можливий результат фінального рахунку.

Підрахуємо ймовірність для кожного значення випадкової величини X-кількості шайб (рис. 3.5) і побудуємо многокутник розподілу (рис. 3.6) забитих у магчі шайб командами «Білий Барс» та «Донбас» (Донецьк)

Кількість шайб	«Донбас» (Донецьк)	«Білий Барс»
0	0,00	0,48
1	0,01	0,35
2	0,03	0,13
3	0,03	0,03
4	0,10	0,01
5	0,14	0,00
6	0,15	0,00
7	0'15	0,00
8	0,12	0,00
9	0,09	0,00
10	0,06	0,00
11	0,04	0,00
12	0,02	0,00
13	0,01	0,00
14	0,01	0,00
15	0,00	0,00

Рис. 3.5. Розподіл випадкової величини Х-кількостізабитих голів

 

 

 

 

 

 

 

 

 

 

 

Рис.3.6Многокутник розподілу кількості шайб команд «Білий Барс» та «Донбас» (Донецьк)

Проаналізувавши дані та графік, можна побачити, що ймовірність того, що «Білий Барс» заб’є одну шайбу — 0,48, а «Донбас» (Донецьк) — 0.1, навпаки, імовірність того, що «Білий Барс» заб’є сім шайб — 0, а «Донбас» (Донецьк) — 0,15.

Припустимо, що «Білий Барс» гратиме на полі команди «Компаньйон-Нафтогаз» (Київ) (рис. 3.7), яка посідає передостаннє місце в турнірній таблиці, «Білий Барс» — гість, «Компаньйон-Нафтогаз» (Київ) — господар.

Коефіцієнт сили атаки «Білого Барсу» дорівнює відношенню кількості шайб, які команда забила на чу­жому полі, до кількості гостьових матчів до середньої кількість голів, узагалі забитих гостями поля коефіці­єнт сили атаки «Білого Барсу» = 21 : 4 : 4,81 = 1,09, коефіцієнт сили атаки «Компаньйон-Нафтогаз» (Київ) = відношення кількості шайб, які команда за­била вдома до кількості домашніх матчів до середньої кількості голів, взагалі забитих господарями поля коефіцієнт сили атаки «Компаньйон-Нафтогаз» (Київ) = 6:5: 5,09 ~ 0,24, коефіцієнт сили захисту «Білого Барсу» = відношення загальної кількості пропущених шайб за останній сезон у гостях до кіль­кості матчів до середньої кількості пропущених шайб усіма командами турніру: коефіцієнт сили захисту «Білого Барсу» = 13 : 4 : 4,81 ~ 0,68.

Коефіцієнт вийшов менше 1, а це означає, що «Бі­лий Барс» пропускав на 32 % шайб у гостях менше, ніж у середньому інші команди турніру.

Тепер, знаючи коефіцієнти сили атаки та захисту, можна розрахувати ймовірність для випадкової величини X-кількості забитих та пропущених шайб: коефіцієнт шайби команди «Білий Барс» = сила атаки «Білий Барс» сила захисту команди «Ком­паньйон-Нафтогаз» (Київ) середня кількість шайб, забитих гостями поля. Маємо: середня кількість шайб команди «Білий Барс» = 1,09* 0,98 *4,81 ~ 5,14.             

Розрахуємо за тією ж формулою кількість голів, які може забити «Компаньйон-Нафтогаз» (Київ): середня кількість шайб команди «Компаньйон-Нафтогаз» (Київ) = сила атаки «Компаньйон-Нафтогаз» (Київ) сила захисту команди «Білий Барс» середня кількість шайб, забитих господарями поля. Маємо: середня кількість шайб команди «Компаньйон-Нафтогаз» (Київ) = 0,24* 0,68 * 5,09 = 0,83.     5,14:0,83 — можливе значення фінального рахунку.

Підрахуємо ймовірність для кожного зна­чення випадкової величини X-кількості шайб (рис. 3.8) і побудуємо многокутник розподілу (рис. 3) забитих у матчі шайб командами «Білий Барс» та «Компаньйон-Нафтогаз» (Київ)

 

		І	В	ВО	ПО	П	Голи		0
Компаньйон		10	1	1	1	7	10-73	1,0-7,3
Нафтогаз	Удома	5	1	0	1	3	6-25	1,2-5,0
Київ	У гостях	5	0	1	0	4	4-48	0.8-9,6

Рис. 3.7. Результативність команди «Компаньйон-Нафтогаз» (Київ)

Звісно, таке моделювання не може на 100 % перед­бачити остаточний результат матчу. Якщо команді «Компаньйон-Нафтогаз» (Київ) вдасться забити три шайби, то матч може закінчитися нічиєю або навіть перемогою.

ВИСНОВКИ

Математика потрібна в будь-якому виді спорту. Тренер без математики не виховає спортсмена чемпіона. У сучасній економіці спорту досить широко використовують математичний апарат — аналізують графіки різних залежностей, виводять математичні формули, проводять математичну обробку статис­тичних даних. Математика, а особливо прикладна математика, пояснює багато послідовностей та зако­номірностей у спорті. За допомогою математичних моделей може бути вирішено практичних завдань у спорті, що допоможе спортсменам і тренерам досягти найвищих результатів.

Математична статистика відіграє величезну роль під час аналізу даних ігор, оцінювання фізичної форми спортсменів. Математичні моделі допомагають оптимально розподіляти змагальний процес, не затя­гуючи  змагання й даючи можливість спортсменам і тренерам оптимально спланувати виступ спортсмена на іграх.

Не так уже й часто в результаті вивчення мате­матичної моделі вдається знайти єдине оптимальне рішення. У більшості випадків удасться лише звузити коло пошуку оптимальних рішень (яких може бути кілька), прийняти рішення, наближені до оптималь­них. Однак і це є успіхом, бо суттєво полегшує завдання особи, відповідальної за прийняття рішень. Тому я вважаю, що матеріали мого дослідження дають можливість розширити межі застосування математичного моделювання в хокеї та допомогти хокейним командам спрогнозувати ймовірність виграшу в матчі.