Опис досвіду роботи на тему "Робота з обдарованими дітьми"

![]()
Матеріали
учасника районного конкурсу
програм та методичних доробок
для роботи з обдарованими дітьми,
вчителя математики Сокальської загальноосвітньої школи I-III ступенів №4
та керівника творчого об’єднання юних математиків Сокальської МАН
Кровіцької Лариси Ярославівни
(номінація методичні доробки педагогів )


«Учитель-скрипаль дитячих душ,як поведе смичком , таку мелодію й почує…»

«Любити свого учня всяким:талановитим чи не дуже, веселим чи сумним, спокійним чи непосидючим…Спілкуватися з ним,навчати й радіти,бо учень-це свято,яке триває доти,поки ти є разом з ним»
Шлях
«Через терни до зірок»
до серця обдарованої дитини
(опис досвіду роботи
з обдарованими дітьми)

Яке це щастя - на урок іти,
Як на побачення…
І скільки років викладаєш ти – не має значення.
В твоєму серці хвилювання вир:
Як зацікавити?
Щоб в кожнім серці доброта і мирЩоб не злукавити.
Так розповісти,
Щоб забило дух
Словами чистими.
Щоб тільки правду,
щоб почався рух думок до істини.
Що за професія така –
Нервова начебто й важка,-
А ти без неї – вже не ти.
Дзвінок. Час на урок іти.
ЗМІСТ
ВСТУП
РОЗДІЛ I ІННОВАЦІЙНІ ПІДХОДИ ДО НАВЧАННЯ ОБДАРОВАННИХ ДІТЕЙ НА УРОЦІ.
1.1 Урок – формування самостійної компетентності здібного учня…………………………………………………………………………………….
1.2 Форми та методи роботи з обдарованими дітьми………………………………............................................................................
РОЗДІЛ II ОБДАРОВАНІСТЬ У ШКОЛІ – ЗДАТНІСТЬ ДО НОВИХ МЕТОДІВ І ЗМІСТУ ПІЗНАННЯ ТВОРИТИ САМОГО СЕБЕ
2.1 Робота з обдарованими учнями в контексті підготовки до районних та обласних олімпіад…………………………………………………………………
2.2 Клуб «Едісон» - індивідуальна траєкторія розвитку обдарованого учня
2.3 Конкурс «Кенгуру» - конкурс виховання успіхом……………………………..
РОЗДІЛ III МАН –ОСВІТНІЙ ПРОСТІР ЖИТТЄВОТВОРЧОСТІ ОСОБИСТОСТІ,ЯК ІНДИКАТОР ПОТЕНЦІЙНОЇ ОБДАРОВАНОСТІ
3.1 «Перемога» - результат роботи команди обдарованих дітей на турнірі..
3.2 Науково-дослідницька робота – шляхетний приклад виявлення обдарованості. …………………………………………………………………….
3.3 «Крок до знань» -ще один крок до реалізації талановитої особистості….
3.4 «Від ідеї до проекту»- вперед до розквіту!...........................................................
3.5 Фестиваль математики - фестиваль творчості………………………………….
3.6 Науково-практична конференція присвячена пам’яті І.Г Каспрука…………..
РОЗДІЛ IV «ТІЛЬКИ В ПРАЦІ НЕВТОМНІЙ КРИЛАТИМ СТАЄШ»
4.1 Робота над собою – запорука успіху…………………………………………….
4.2 Особистий приклад учителя в розвитку обдарованої дитини………………...
ВИСНОВКИ
ВСТУП
Обдарованість дитини…Що це таке? Можливо це своєрідна іскра Божа, яку треба відшукати в її душі, і допомогти не тільки не згаснути, а спалахнути полум’ям. Здібні ,талановиті люди – рушійна сила народу, це величезне багатство, неоціненний статок. Саме інтелектуальними зусиллями обдарованих дітей забезпечується прогрес людства, плодами якого користуються всі.
Обдаровані діти – майбутній цвіт нації, інтелектуальна еліта, гордість і честь України, її світовий авторитет, а тому перед кожним вчителем стоїть завдання спрямоване на забезпечення формування інтелектуального потенціалу нації, шляхом створення оптимальних умов для розвитку всебічно обдарованої молоді.
Обдарована дитина – обличчя нової школи, школи - життя. Саме тому розвиток творчих здібностей її набуває на сьогоднішній день особливої актуальності, потребує якісно-нового підходу на кожному кроці діяльності. Розвиток творчих здібностей особистості – це одвічний гуманний принцип. Ще стародавні греки вважали, що самостійна, а отже і творча особистість здатна самовіддано служити своєму народу і державі. Кожна держава зацікавлена у вихованні такого могутнього інтелектуального потенціалу, як обдаровані талановиті діти.
Чи легко їм, обдарованим дітям? Шлях «Через терни до зірок» чекає їх попереду: шлях, скроплений сльозами поту наполегливої праці, терпіння, недоспаних ночей, невтомної роботи над собою, критики з боку інших. І все це для того, щоб відчути радість перемоги, увінчатися вінцем слави науки.
Ми, сучасні вчителі, з Божою ласкою повинні побачити таку дитину, і вміло, підтримуючи за плечі, вести за руку по ниві науки.
«Знайти, не втратити, не загубити, а «розпустити маленький пуп’янок» у чудову квітку науки, аромат якої запам’ятється надовго» - моє творче гасло при роботі з обдарованими дітьми.»
Твердо знаю і завжди пам’ятаю, що:
- кожна дитина має задатки;
- кожна особистість прагне реалізувати свої здібності.
Здібності та задатки розвиваються та реалізуються при умові сприятливого зовнішнього середовища. Ми визначаємо обдаровану дитину, як таку дитину, що відрізняється від однолітків вираженими здібностями, має внутрішні передумови для високих досягнень, в тому або іншому виді діяльності. А під здібностями ми розуміємо індивідуальні особливості, які дозволяють при сприятливих умовах успішно оволодівати діяльністю.
Кажуть, що талант завжди родом із дитинства і що кожна дитина народжується із зернятком у руці. Тільки треба знайти поле, де це зернятко найкраще проросте. Моє завдання – допомогти дитині розвинути свій дар, скористатися своєю унікальністю з користю для себе та оточуючих. Діти різні. У когось Божа іскорка яскрава і не потребує зусиль для подальшого розквіту, у когось талант прихований, пригнічений комплексами, а тому вимагає клопіткої праці, психологічної підтримки. « Вміння знаходити обдарованих та здібних дітей – талант, вміння їх вирощувати – мистецтво » , - говориться в народній мудрості. Цю істину, як теорему в математиці, я доводжу своєю працею.
Обдаровані діти – це капітал майбутнього нашої країни, а їх виховання та освіта, створення для таких дітей розвивального середовища є основним завданням кожного вчителя. Я щиро переконана, що не має необдарованих дітей. Треба лише допомогти відшукати дар у кожному. Підтримати і розвинути його.

- Урок – формування самостійної компетентності здібного учня.
Урок – дзеркало загальної
педагогічної культури вчителя,
мірило його інтелектуального багатства…
До хорошого уроку вчитель готується все життя.
В. Сухомлинський
Гарний урок неможливий без натхнення і педагогічної інтуїції.
Саме тоді він – результат творчості, а не ремесла. Разом з тим. гарний урок – це втілення спланованого задуму вчителя. Сума знань, яку одержують учні у сучасній школі, повинна сприяти розвитку особистості.
Обдарованість – високий рівень здібностей дитини ,що дозволяє їй досягти особливих успіхів на уроці математики. Обдаровані діти вільно і швидко оволодівають відповідними вміннями і навичками. Немає потреби примушувати їх вчитися, вони самі шукають собі роботу, частіше складну, інтелектуальну, із задоволенням нею займаються, показуючи високий рівень навчальних досягнень. Такі діти часто перебільшено емоційні, запальні, легко збуджуються через дрібниці, але як показує власний досвід це не вередування, а виявлення багатства натури.
Обдаровані діти – це діти, які різко виділяються із середовища ровесників розумовим розвитком, що є наслідком, як природних задатків, так і сприятливих умов виховання. Досить важливо не втратити такої дитини, котра прийшла в 5 клас з молодшої школи. Через декілька уроків вимальовується картина, спереду якої вона – здібна, творча, обдарована особистість, здатна розв’язувати буть яку проблему поставлену перед нею, спотикаючись, шукаючи правильний розв’язок, випереджаючи інших.
Мартін Бубер писав: «З народженням кожної дитини в світ вноситься щось нове, чого ще не було, щось первозданне і неповторне. Обов’язок вчителя – знати і не забувати, що він у світі єдиний у своїй якості…». Керуючись цими словами моя робота з обдарованими дітьми на уроці математики грунтується на диференційованому підході, що сприяє створенню умов для оптимального розвитку такої дитини, а саме розкриває потенціал креативності, як показник обдарованої дитини. Це одна з найголовніших умов розкріпачення свідомості – її вихід за межі наявного, піднесений, узагальнений погляд на речі, це крок свідомості у світ свободи і творчості.
К.Д. Ушинський писав про те, що дитина, яка отримала щасливе поєднання інтелектуальних і творчих здібностей, має можливість скористатися ними у майбутньому. Саме тому на своїх уроках керуюсь теорією розв’язання винахідницьких завдань, кінцевою метою яких є свідоме досягнення стану «Осяяння».
Мої учні – реалісти. Вони люблять розв’язувати задачі пов’язанні з життям, задачі. відповіді яких відповідають реальності. На своїх уроках я використовую теорію відносності, вчу співставляти, порівнювати, прогнозувати результати. Досить часто учні з неординарним мисленням самі складають задачі і радіють іншим учням котрі їх розв’язують.
З власного досвіду можу сказати, що здібні діти відрізняються на уроках математики допитливістю, наполегливістю у пошуку відповідей, хорошою пам’яттю вмінням ставити глибокі запитання, схильністю до роздумів, яскравістю пізнавальної активності, креативністю мислення, високою здатністю до концентрації уваги високим рівнем фантазії і великим прагненням до «успіху». У них постійно рука піднята до гори, вони хочуть оцінки кожного уроку, що мною дуже цінується, багато працюють самостійно. Така дитина завжди чекає на похвалу, на те, що я – вчитель, маю розділити з ним радість його досягнень.
Одаровані діти часто є оригінальними на уроці: у своїй поведінці та спілкуванні, монотонна праця викликає в них набридання. Через те на уроках я роблю хвилинки на яких розв’язую ребуси, головоломки, що сприяють розвитку пам’яті, уваги, кмітливості.
Велику увагу приділяю самостійній праці учнів з літературою, вчу аналізувати та систематизувати прочитаний матеріал, робити висновки. У старших класах пропоную уроки – семінари, уроки – консультпункти, на яких обдаровані діти – проявляють свою майстерність, проводять майстер – класи, готуючись до них вдома. При підготовці до таких уроків в учнів виробляється здатність прогнозувати можливі ситуації, способи розв’язання проблем, а також знаходити можливі виходи із проблемних ситуацій. На таких уроках спостерігається синергетичний ефект: вчитель + обдарована дитина = якісний урок. Творчі учні не уникають на таких уроках відповідальності, пред’являють високі умови до себе, самокритичні. З іншого боку, не люблять коли до них ставляться із захопленням, обговорюють їхню винятковість, талановитість, адже самі знають собі ціну. Ці діти – приклад для наслідування. До них тягнуться інші діти, стараються працювати краще, на результат.
Моя співпраця у старших класах з творчою особистістю на уроці формує здатність в дитини довільно регулювати свої дії, обгрунтовувати свою позицію і приймати точку зору іншого, якщо вона більш обгрунтована. На перший план ставлю перед собою завдання не по накопиченню дитиною інформації, а засвоєння інтелектуальних технік. Для цього складаю алгоритми, які діти застосовують для розв’язування задач, придатних для застосування в різних життєвих ситуаціях. Саме інтелектуальна техніка є початком життєвого успіху школяра, його потенційного аспекту, в основу якого покладена життєва перспектива. Як приклад цього всі мої учні люблять уроки математики, і біжать на них з радістю.
При роботі з обдарованими дітьми, готуючись до уроку підбираю завдання на матеріалі довкілля та знань українських народних традицій, завдання комбінаторного типу та задачі з логічним навантаженням. Практикую використання цікавинок, задач –казок, тематичних загадок. Мої діти навчені самі писати твори з тої чи іншої математичної теми, писати листівки-розповіді воїнам АТО про свої досягнення, кращі з яких зачитуються на хвилинці розвантаження на уроці.
Розвиваю евристичний рівень творчої активності особистості: організовую навчальний процес у вигляді ділової гри, - з розподілом ролей, вибором стратегії поведінки, планування дій наперед. Як результат – продуктивне спілкування вчителя з учнем та учнями між собою. Розвивається математична мова, яка надзвичайно бідна у сучасних учнів. Працює уява, характерне напруження думки, вольових зусиль, вияв емоцій, які значно бурхливіші у обдарованої особистості.
При роботі з обдарованими дітьми практикую уроки «прес-конференції» , «телемости» , «інтерв’ю» , «ринги» , нестандартні уроки, які підтверджують важливість даної теми і її практичне застосування. Так, на уроці «Застосування звичайних дробів» кульмінаційним моментом був торт, і кожна дитина на все життя запам’ятала, що 1/25 торта сьогодні дісталась їй (див.додаток 1) Проводжу так звані уроки-екскурсії. Восени разом з дітьми йду в парк при вивченні тем «Масштаб» , «Площі» , «Периметр». Нещодавно провела нестандартний урок на виставці «Трагічні скрижалі української науки» на якій учні познайомилися із забутими і незнаними вченими-математиками : Миколою Чайківським, Михайлом Кравчуком, Ігором-Орестом Богачевським. Такі уроки змушують дитину іншими очима дивитись на світ, по-іншому працювати на уроці, відноситись один до одного. (див.додаток 2 ) Співробітництво в процесі такої роботи формує в першу чергу в обдарованих дітей уміння приймати певну точку зору, узгоджувати свою думку з думками інших. При цьому у творчої особистості виникає багато ідей, які вона висуває і не боїться висловлюватися.
На уроках обдаровані діти хочуть вчитися і досягають успіхів. Навчання приносить їм задоволення, і вони набувають знання, не сприймаючи заняття, як насилля над собою. Вони задають багато запитань і зацікавлені в тому, щоб якнайшвидше отримати відповідь на них. Такі особистості дуже активні і завжди чимось зайняті. Вони прагнуть працювати більше за інших. Моя роль – диригента, який вміє знайти цікаву роботу дітям, зробити все для того, щоб творча особистість на уроці не дрімала.
З власного досвіду знаю, що запорукою успіху на уроці є хороший настрій. Між мною і учнями в процесі роботи повинні бути дружні відносини, які впливають на результат, і стимулюють бажання обдарованої дитини працювати заради праці, а не заради прагнення обігнати інших. Моя праця і учня на уроці стає співтворчістю, при якій кожен буде вносити свій посильний внесок у досягнені спільного успіху.
Правильно кажуть, що талановита людина повинна зуміти на уроці розвинути дарування, відшліфувати свої здібності і правильно скористатися ними з користю для себе і для людей, але вдається це далеко на всім і всякому разі не відразу.
У народі кажуть «Чого Іванко не навчився, того Іван не буде знати». Моє завдання підготувати обдаровану дитину до життя з раннього дитинства, розвинути математичні здібності, які прогнозують інтелектуальний потенціал дитини. Індивідуальну роботу з обдарованими дітьми починаю не в старших класах, а з молодших та середніх.
На уроках математики я стараюся дарувати учням радість і насолоду від процесу пізнання, вчу діяти в ситуації підвищеної складності, «заражаю» здібну особистість інтересом до творчої діяльності та потребою в ній, формую особистий «сценарій переможця»

1.2 Форми та методи роботи з обдарованими дітьми.
«Талант – то крапля здібностей і море праці»
Григор Тютюнник
Цей влучний вислів належить відомому українському письменникові. І з ним важко не погодитись: кому , як не людині, що за життя скуштувала і солодкого смаку слави, і жорстокого диктату у своїй діяльності, знати, як непросто жити з унікальним даром, даним людині Богом чи успадкованим від батьків. Тим більше – працювати над тим, аби талант цей розвинути, філігранно відточити, вміти застосувати…
Моє завдання розвивати дитячий талант, філігранно відточувати і вказувати йому належний шлях застосування, використовуючи різні форми та методи на уроці. Обдаровану дитину не можна не помітити, вона завжди кидається в очі, виділяється серед інших своїми схильностями і можливостями в будь-якому виді діяльності.
Кожен урок має сіяти в дитячих душах Добро та Красу, формувати людяне в людині. «Щоб зворушити, треба самому бути зворушеним. Щоб радувати, просвітлювати душевний світ, треба нести просвітленість у своєму серці, а серце нести високо», - писав О.П. Довженко. На уроці я все обмірковую до дрібниць, зважаючи на внутрішній стан дитини, тому впроваджую емоційні хвилинки ,які створюють особливе тло заняття, його інтригуючий початок, без цього не можна створити на уроці сприятливий психологічний клімат, викликати інтелектуальні почуття подиву, очікування нового.
Сучасний урок має бути розумним, цікавим, захопливим і радісним. Для цього в своїй практиці я використовую такі прийоми, як «емоційне стимулювання» - констатую незначний успіх дитини, вселяю віру в себе, «авансування» - репетиція майбутньої дії, що створює настанову на успіх, «даю шанс» - готую вдома задачі, розв’язуючи які творча особистість отримує можливість несподівано для себе розкрити свої здібності. Власна практика підтверджує, що не через насичення дитячої свідомості, великою кількістю фактів і теоретичних відомостей досягається справжня мета навчання, а лише через задоволення внутрішнього прагнення дитини вирости до рівня обдарованості, відчути радість пізнання і творчості.
З метою розвитку творчих здібностей обдарованих дітей створюю на уроці проблемні ситуації, що вимагають уяви, прогнозування, пропоную цікаві факти, технічні та наукові ідеї, стимулюю оцінкою і підтримую ініціативу учнів, самостійність. Підкидаю проекти, які можуть захоплювати. Підхоплюю думки учнів і оцінюю їх одразу, підкреслюючи їх важливість і оригінальність, навчаю дітей систематичної самооцінки кожної думки, виробляю терпиме ставлення до нових понять, думок. Вчу доводити починання до логічного завершення.
Практикую на уроках в середніх класах театралізовані свята, як особливу форму роботи з обдарованими дітьми, оскільки в них діти мають можливість не тільки реалізувати акторські здібності, а й творчо розв’язати математичну проблему, очима творчості подивитись на математику. Проводжу вікторини, математичні диспути, котрі виявляють ерудицію й дослідницькі навички, сприяють підвищенню мотивації обдарованих дітей. Розв’язуючи ребуси, кросворди, діти поступово починають складати власні задачі, головоломки, що розвивають творчу уяву мислення, що є основою формування ейдетичного мислення, в основі якого запам’ятовування інформації через образи, асоціації, відчуття.
В процесі навчання поєдную ерудиції з вільним володінням розумовими аналітичними діями, що приносить успіх. Паралельно з розширенням кругозору застосовую завдання на порівняння, абстрагування, аналіз – синтез, індукція – дедукція.
При роботі з творчими особистостями підбираю цікаві завдання, нестандартний розв’язок яких приводить їх у захват, розвиваючи у них почуття прекрасного. Невтомна праця приносить їм задоволення, вони швидко набувають високого рівня витривалості.
На мою думку, найбільше спонукають учнів до творчості технології ситуативного моделювання. У сучасному суспільному житті ми спостерігаємо дебати партій, політиків, ток-шоу з відомими діячами, презентації фірм, дискусії перед мікрофоном, різні реклами. Елементи таких заходів уплітаються в сучасний урок. На своїх уроках я застосовую такі технології ситуативного моделювання: метод реклами, метод презентації, метод проектів, рольову гру.
Кожен з методів і форм навчання має певні переваги і недоліки. Ефективність їх застосування визначається конкретикою процесу навчання. Я самостійно приймаю рішення про використання того чи іншого методу на основі свого власного досвіду, врахування особливостей дитини , з метою максимальної ефективності процесу навчання. Навчальні заняття для мене та моїх учнів – постійний пошук, спільна праця, в основі якої довіра та спільне бажання досягнути бажаний результат, адже педагогічний пошук – це пошук інноваційних технологій, форм та методів, які сприяють особистому розвитку обдарованої дитини.
2.1 Робота з обдарованими учнями в контексті підготовки до районних та обласних олімпіад.
«Людина ,що володіє вродженим талантом,
відчуває найбільше щастя тоді,
коли використовує цей талант.»
Йоганн Вольфганг Гете
Обдарована дитина має творчий, нетрадиційний, особистий світогляд. Вона завжди готова до перегляду своїх поглядів, до постійного самовдосконалення, цілеспрямована і наполеглива. Кожного року мої учні беруть участь у районних та обласних олімпіадах з математики. Олімпіада - це позакласна форма навчання обдарованих дітей. Для вчителя математики підготовка до олімпіад є благодатним полем експериментальної діяльності. Всі творчі знахідки, методичні наробки можуть бути впроваджені в педагогічну практику й принести вагомі результати.
Процес підготовки до олімпіад є системним, неперервним, спланованим на перспективу. Оцінюється велике бажання обдарованої дитини працювати в позаурочний час. Організовую індивідуальну роботу, практикую роботу в групах. Підготовка до олімпіади починається з того, що олімпіадні діти, ще літом ведуть повторення теоретичного матеріалу, повторюють методику розв’язування деяких типів задач. Починаючи з вересня місяця, з дітьми розв’язую задачі минулого олімпіадного сезону, пропоную нові задачі з різних років і різних рівнів олімпіад, проводжу заняття у формі «міні олімпіад» для поступового психологічного налаштування учнів.
Всі бажаючі беруть участь у шкільній олімпіаді. Підбираю завдання диференційовані, репродуктивного характеру, які може розв’язати більшість учасників й завдання II і III етапів олімпіади , які потребують творчого підходу до розв’язання.
Під час підготовки до олімпіади використовую метод роботи з обдарованими дітьми – проблемні запитання. Підбираю такі запитання, на які не має готової відповіді. В запитання закладаю проблемну ситуацію розв’язати яку потрібно неординарним способом. Розвивається логічне мислення, формується творчий потенціал здібної дитини.
Побудова гіпотез – ще один із методів роботи при підготовці до олімпіади. Здібні діти висувають власні гіпотези щодо вирішення наукового завдання. Роблять свої припущення, що можуть стати темою дослідження на майбутнє. Застосовую «ефект Розенталя » , який є основою методу «Виділяти найкраще». Цей метод дозволяє стихійно «керувати» поведінкою дитини і приводити до очікуваних результатів. Кінцевим ефектом цього методу є похвала учня вчителем, висловлена з ентузіазмом. Наголошую на будь – яких поліпшеннях, відмічаю кожен маленький, але успішний крок на шляху до виконання завдання.
У період підготовки до олімпіад звертається увага на вміння володіти собою, вміло користуватися здобутими знаннями в умовах конкуренції, стресу. Враховується вміння не тільки приймати перемогу, уникаючи "зіркової хвороби”, а й витримувати невдачу, за будь-яких умов поважати однолітків-конкурентів. Важливим аспектом у підготовці олімпійця є виховання порядності, формування переконання: найцінніша перемога – та, що здобута чесно, своїми силами.
При підготовці до районного та обласного етапів олімпіади ознайомлюю учнів з авторськими розв’язками завдань, розв’язками завдань з різних збірників, практикую тестову підготовку, онлайн тестування завдань підвищеної складності. « Досвід- дитина думки, а думка – дитина дії. Дії – головний ключ до успіху, до результату». І як результат – мої учні щорічно є переможцями районного етапу олімпіади з математики і учасниками обласного етапу:
2012-2013 н.р- Левчук Ірина(10 клас) – I місце
2012-2013 н.р - Мігус Роксолана(10 клас) -– III місце
2013-2014 н.р - Мігус Роксолана(11 клас) -– III місце
2014-2015 н.р – Середа Софія (9 клас) – I місце, Волошин Іван(10 клас)– III місце
2015-2016 н.р – Середа Софія(10 клас)- II місце, Волошин Іван(11 клас) – III місце
2016-2017 н.р - Ксенюк Анна(9 клас) -I місце, Середа Софія(11 клас) – III місце;
Здібна дитина розв'язуючи задачі, готуючись до змагань повинна бути цілеспрямованою і наполеглевою , володіти емоційною стабільністю, мати схильність до самоаналізу. Я, як сіяч розумного, доброго, вічного повинна бути готова до виконання різноманітних обов'язків пов'язаних із навчанням обдарованих дітей, постійно підвищувати свою професійну майстерність, мати живий та активний характер, високий рівень інтелектуального розвитку, бути доброзичивим і чуйним, розбиратися в особливостях психології обдарованих дітей відчувати їх потреби та інтереси.


2.2 Клуб «Едісон» - індивідуальна траєкторія розвитку обдарованого учня
«У кожній людині сонце.
Тільки дайте йому світити».
Сократ
Клуб «Едісон» - творче об’єднення обдарованих учнів, створене у 2012 році, з метою розвитку їх здібностей і обдарувань, самовизначенню з напряму дослідницької роботи з математики. Основними завданнями наукового товариства є:
- Розвиток та підтримка обдарованих учнів;
- Створення умов для розвитку здібностей дітей до самостійної дослідницької діяльності, формування творчої особистості;
- Поглиблення знань учнів, формування умінь і навичок наукового дослідження;
- Виховання якостей наукового фахівця, патріота України, особистості високої духовної культури.
Робота в клубі забезпечує творчий, інтелектуальний, духовний розвиток, підготовку до майбутньої професії та громадської діяльності. Я, як голова клубу «Едісон», кожного року складаю план роботи наукового товариства, згідно якого здійснюється робота з обдарованими дітьми.
На першому занятті засідання допомагаю учням обрати тему дослідження до душі, що не аби як впливає на кінцевий результат, адже не дарма кажуть «Велике діло- початок». З вересня по листопад допомагаю учням опрацьовувати літературу, вести пошукову роботу, пояснюю невідомі терміни і теми. В січні місяці відбувається друге засідання клубу на якому творчі особистості захищають науково – дослідницькі роботи. З кожним роком кількість робіт над якими працюють діти збільшується. За 6 років мої учні, слухачі клубу «Едісон», написали такі роботи:
- 2012 рік: « Похідна та її застосування» ( Пальчук І.), «Теорема Чеві та Мінелая» (Рябова А.) , «Ціла та дробова частина числа» (Мігус Р.), «Функціональні рівняння» (Левчук І.);
- 2013 рік: « Застосування похідної до розв’язування задач практичного змісту» ( Гнотик В.), «Розв’язування рівнянь вищих порядків з веденням до нерівностей» ( Владика В.) «Застосування комплексних чисел до розв’язування арифметичних та тригонометричних задач» (Уманська Х.), «Математичні відкриття впродовж століть у літературі» (Бобешко А.) , «Розв’язування логічних задач» (Ферко А.).
- 2014 рік : «Божественна пропорція – як прояв гармонії в навколишньому світі ( Мігус Р.), «Графіки та їх функції» (Левчук І.), «Числа Фібоначчі» (Мігус В.), «Визначники н-го порядку» (Волошин І.), «Застосування методу введення допоміжної змінної при розв’язуванні рівнянь олімпіадного характеру» ( Шевчук Н.).
- 2015 рік : «Математика у як основа мистецтва управління» (Волошин І.), «Розв’язування економічних задач на уроках математики за допомогою лінійного програмування» (Шувчук Н.), «Зв’язок музики і математики» (Воробій Я.), « Теорія ігор» (Предземірський В.), «Розв’язування задач економічного характеру» (Сологуб К.)
- 2016 рік : «Функціональні рівняння» ( Ковальчук А.), « Розв’язування тригонометричних рівнянь з параметрами» (Семенюк Н.), «Застосування властивостей функцій до розв’язування рівнянь» ( Середа С.), «Діофантові рівняння» ( Мартинюк Р.) (Додаток3)
2.3 Конкурс «Кенгуру» - конкурс виховання успіхом
Успіх часто буває
єдиною видимою різницею
між генієм і безумством.
П’єр Буаст.
Кожна дитина по-своєму неповторна. Вона приходить у цей світ щоб знайти себе. Скільки дітей – стільки й здібностей. Міжнародний конкурс «Кенгуру» створює у школі період творчої активності. Я переконую творчу особистість, що участь у цьому конкурсі розвиває критичне мислення ,самостійність. здатність дитини до прогнозування, уяви, творчого мислення. Дитина практично розв’язує дослідницькі завдання пов’язання з життям. Мої учні дуже люблять цей конкурс. Залюбки розв’язують завдання попередніх років і з нетерпінням чекають нових. Кожного року залучаю до участі в цьому конкурсі багато дітей школи, кількість яких зростає щороку. Статистика участі в конкурсі власне моїх вихованців:
- 2010-2011 навчальний рік -18 учасників (7 золотих і 8 срібних сертифікатів);
- 2011-2012 навчальний рік – 21 учасник (20 золотих і 1 срібний сертифікат);
- 2012-2013 навчальний рік – 26 учасників (14 золотих і 12 срібних сертифікатів);
- 2013-2014 навчальний рік – 24 учасники (12 золотих і 12 срібних сертифікатів);
- 2014-2015 навчальний рік – 18 учасників (15 золотих і 3 срібних сертифікати);
- 2015-2016 навчальний рік – 23 учасники ( 12 золотих і 11 срібних сертифікатів).
Як координатор конкурсу «Кенгуру» в школі у 2016-2017 навчальному році залучила до участі 89 учасників в осінньому етапі і 90 учасників в весняному етапі конкурсу, у 2015-2016 навчальному році 93 і 78 учасників, у 2014-2015 навчальному році 92 і 73 учасники, у 2014-2015 навчальних роках 80 учасників.
Діти люблять конкурс, радіють своїм успіхам і розділяють радість з іншими. В конкурсі не має переможених: відмінний ,добрий, сертифікат за участь – це успіх кожного.
Я, як координатор конкурсу постійно підвищую свою професійну майстерність на семінарах, конференціях організованих Львівським фізико-математичним ліцеєм. Знання, здобуті там, допомагають мені при роботі з обдарованими дітьми. В свою чергу, допомагаю талановитій особистості реалізовувати себе, і тим самим зобов’язана не втратити обдаровану дитину, бо, втрачаючи талант, обдарування, здібність, я встрачаю майбутнє.
Проявляю терплячість, безмежно вірю в дитину, знаю, що ця дитина виросте хорошою творчою людиною. (додаток 4)
3.1 «Перемога» - результат роботи команди обдарованих дітей на турнірі
Математичний турнір-бій заради краси математики.
Обдарована дитина – це така дитина, яка демонструє розвиток здібностей, вищий за здібностей однолітків, це сукупність здібностей, що дозволяють творчій дитині брати участь у різноманітних конкурсах і досягати вагомих результатів.
Одним із конкурсів, якого учні мої є активними учасниками є Всеукраїнський турнір юних математиків імені Миколи Ядренка. Задачі цього конкурсу є надзвичайно складні, авторські і розв’язки до них є нестандартними. Для того щоб розв’язувати такі задачі потрібно мені, як керівнику підготовки учнів до турніру, володіти багатьма питаннями вищої математики і зуміти передати їх дітям. Саме така робота вимагає належної змістовної наповненості занять, зорієнтованості на новизну інформацію та різноманітні види пошукової, розвиваючої, творчої діяльності. Диференційована, індивідуальна групова робота з обдарованими дітьми, які під час занять вчаться працювати в команді, на чолі з капітаном, приносить позитивні результати.
Зацікавивши учнів розв’язками, вселивши в них впевненість в собі, дух перемоги, ми впевнено крокуємо «по полі» вищої математики. Учасники команди постійно намагаються вирішувати проблеми, здавалося б які їм не під силу, «занурюються» у світ не зрозумілих позначень і символів, але вода камінь точить і приводить до певного результату: кожного року мої учні є призерами обласного етапу Всеукраїнського конкурсу імені М. Ядренка:
- 2011-2012 навчального року – III місце (Уманська Х., Мігус Р., Левчук І., Савчук Т.) ; Капітан команди – Мігус Роксолана
- 2012-2013 навчального року – III місце (Левчук І., Уманська Х., Мігус Р., Кобяк О., Зарнаваницький С.) ;Капітан команди – Левчук Ірина
- 2013-2014 навчального року – II місце (Пакулець А., Закалик В., Плюхін В., Сусол О., Войтко К.) ; Капітан команди- Закалик Володимир
- 2014-2015 навчального року – II місце (Верхолюк І., Закалик В., Бачинський Н., Кровіцька У., Дадак Д., Ковальчук Д. );Капітан команди – Закалик Володимир .
- 2015-2016 навчального року – II місце (Бачинський Н., Пономаренко В., Баран А., Закалик В., Ковальчук Д.);Капітан команди – Закалик Володимир.
- 2016-2017 навчального року – II місце ( Бачинський Н., Мачинський Н., Барило Б., Мусій Ю., Пономаренко В.)Капітан команди – Бачинський Назарій.
Цього року команда Сокальської МАН мала почесну місію представляти команду Львівської області на фінальному етапі Всеукраїнського конкурсу імені М. Ядренка у місті Чернівцях. Наші діти Бачинський Назарій, Мачинський Назарій, Барило Богдан назавжди запам’ятають різні способи розв’язання важких задач, радісні очі журі і «плечі» друзів,- однодумців. З 20 команд ми – 12, але це велика перемога для нас, перемога – результат не доспаних ночей, результат наполегливої праці, результат того, що обдарована дитина долає всі математичні труднощі завдяки творчому вчителю і навчальний процес для неї цікавий, різнобічний, результативний.
«Учень…це не посудина, яку потрібно наповнити, а факел, який треба запалити». Факел, запалений у серцях таких дітей буде горіти вічно.
(додаток5)


3.2 Науково-дослідницька робота – шляхетний приклад виявлення обдарованості.
«Вміння знаходити обдарованих
та здібних дітей – талант,
вміння їх вирощувати – мистецтво»
В.О.Сухомлинський
«Кожен учень повинен піднятися на свою маленьку вершину, досягти важливих успіхів»
В.О. Сухомлинський
Властивістю таланту є свідомий, поглиблений, всебічний розвиток обдарованості. У кожній дитині закладені певні здібності, тільки в одних вони виявляються дуже яскраво і виразно, а в інших залишаються дрімати всередині. З власної практики зауважую те, що до написання науково-дослідницької роботи залучаю дрімаючі обдаровані особистості, які не люблять тиску, не мають практичної можливості проявити свої здібності. Ці діти відрізняються гарною пам’яттю, багатим словниковим запасом, вони надзвичайно гостро переживають невдачі, часто вперті і прагнуть довести розпочату справу до кінця. Самостійність, наполегливість, працьовитість, досліджуваність, пошуковість – риси, притаманні таким учням. Вони не тільки повинні засвоїти певну суму знань, а й навчитися спостерігати, порівнювати, виявляти зв’язок між поняттями, міркувати, досліджувати, проводити особисті, індивідуальні дослідження і трактування. Головне моє завдання полягає у тому, щоб ця праця приносила дитині радість, а не муки і гіркоту невдач.
Обдарована дитина яка захоплена дослідницькою роботою виявляє наполегливість, силу волі, критичне ставлення до загальновідомого. В творчості вона може реалізувати всі свої знання, уміння та здібності.
При написанні науково-дослідницької роботи з власного досвіду бачу, що діти прагнуть рівноправного спілкування, щоб їх сприймали як особистості й реагували на них як на творчість. Кульмінаційне завершення такої роботи – захист, на якому вона – обдарована дитина, яка відчула радість своєї перемоги, яка пройшла шляхетний шлях становлення особистості. Мої учні кожного року є переможцями обласного етапу конкурсу – захисту науково-дослідницьких робіт, а саме:
- 2010-2011 навчальний рік – III місце «Діофантові рівняння» (Мігус Р.)
- 2011-2012 навчальний рік - IIIмісце «Розв’язування рівнянь вищих степенів» (Мігус Р.)
- 2012-2013 навчальний рік – II місце «Золотий переріз – божественна гармонія в навколишньому світі» (Козира М.)
- 2013-2014 навчальний рік – II місце «Криві другого порядку» (Іванчина О.)
- 2014-2015 навчальний рік – «Теорія ігор в математиці» (Бачинський Н.) III місце , «Математичне моделювання та прикладні задачі» III місце (Верхолюк І.)
- 2015-2016 навчальний рік – «Випадкова величина та гра, як модель процесу прийняття рішення в умовах ризику» (Бачинський Н.) II місце
- 2016-2017 навчальний рік – «Розділення секрету» (Бачинський Н.) I місце
Залучення учнів до написання науково-дослідницьких робіт сприяє вихованню високоморальних якостей наукового фахівця, свідомого громадянина, патріота України, особистості високої духовної культури.
Триває подальша робота з обдарованими дітьми, при якій я пам’ятаю, що головна потреба сучасного школяра – праця, самостійна думка, відкриття істини, подолання нових вершин. Поважаю дитяче бажання бути на «вершині», бережу його як найтонший рух людської душі, не зловживаю словами, вчинками, даю дітям радість успіху, збуджую в їх серцях почуття гордості, власної гідності. Пам’ятаю про те, що в наших школах не повинно бути нещасливих дітей, душу який гнітить думка, що вони ні на що не здібні. Успіх – джерело внутрішніх сил дитини, як породжують енергії для переборення труднощів, бажання вчитися.
«Навчання обдарованих дітей – не ремесло, а творчість.» , творчість, яку ми розвиваємо, ведемо по творчому пошуку дослідження (додаток6)
3.3 «Крок до знань» -ще один крок до реалізації талановитої особистості.
«Про свої здібності
людина може дізнатися,
тільки спробувавши прикласти їх»,
Сенека
З метою виявлення, розвитку та підтримки обдарованих дітей області, з підвищенням інтересу школярів до поглибленого вивчення математики, та залучення учнів до науково-дослідницької діяльності проводиться в лютому-березні місяці Львівською ОМАН обласний дистанційний математичний конкурс «Крок до знань».
Мої учні є постійними учасниками і переможцями цього конкурсу. Зокрема :
- 2013-2014 навчальний рік: Волошин І. (III місце)
- 2014-2015 навчальний рік: Пономаренко В. (III місце)
- 2015-2016 навчальний рік: Пономаренко В.( II місце)
- Досягненню успіху передує велика робота з тестами, з різними розділами вищої математики, розв’язування однієї задачі різноманітними способами, розв’язування творчих завдань, задач олімпіадного характеру.
Не дарма кажуть, що кожна дитина по-своєму неповторна. Вона приходить у цей світ, щоб творити своє життя, щоб знайти себе. Саме цей конкурс – ще один крок у відшуканні творчої особистості, особистості, яка відрізняється від інших характером рішучості і визначеності, яка не боїться долати труднощі, перешкоди, яка знаходить час розв’язувати задачі пізно ввечері.
3.4 «Від ідеї до проекту»- вперед до розквіту!
«Рано чи пізно
будь-яка правильна ідея
знаходить застосування
в тій чи іншій справі»
О.М Крилов
Активне залучення своїх вихованців до різноманітних районних, обласних, Всеукраїнських конкурсів, змагань, виставок – ще один крок до успіху, крок, який стимулює активність, ініціативу, пошук. Це спонукає учнів до розробки та впровадження власних творчих задумів, створення ситуації вільного вибору, відповідальності за обране рішення. При підготовці до цього конкурсу я застосовую і використовую поради Девіда Льюїса що до розвитку обдарованої дитини, а саме:
- Розвиваю ідею запропоновано дитиною;
- Відповідаю на запитання дитини терпляче і з розумінням важкості;
- Допомагаю дитині приймати рішення;
- Хвалю дитину за навчальну ініціативу;
- Ніколи не вказую на дитячі помилки та невміння;
- Вбачаю в дитячій роботі гідне похвали;
- Спонукаю дитину вчитися вирішувати проблеми самостійно;
- Допомагаю дитині бути особистістю;
- Розвиваю позитивне сприйняття її здібностей.
Пам’ятаю, що для обдарованої дитини творчість є життєвою необхідністю. Тому потрібно готувати її до спостережливості, наполегливості, формувати вміння доводити почату справу до кінця, працелюбність, вимогливість до себе, задоволення від процесу творчості, терпляче ставлення до критики, гордості та почуття власної гідності. Все це приводить до певного результату і перемог:
- 2010-2011 навчального року – II місце «Математичне моделювання», з’єднання елементів будівельних конструкцій» (Мігус Роксолана)
- 2011-2012 навчального року – II місце «Розв'язування рівнянь зведенням до нерівностей з урахуванн
- ям нев'язки» (Козира Мар'яна); нагороджена грамотою і подарунком за роботу «Діофантові рівняння» (Мігус Роксолана);
- 2012-2013 навчального року I місце «Розв’язування рівнянь, що містять обернені функції, методом відображення інтервалів» (Войтко Катерина);
- 2013-2014 навчального року – II місце «Метод областей при розв’язуванні олімпіадних задач» (Лапко Анастасія);
- 2014-2015 навчального року – II місце «Вибір стратегії успіху» (Волошин Іван).
- 2015-2016 навчального року- II місце «Додаткові побудови в стереометрії» Волошин Іван
Мої вихованці працюють на майбутнє, стають цілеспрямованими особистостями. Вміють поставити перед собою чітку реальну мету і прагнуть її досягнення. Вони здатні самостійно мислити, приймати сміливі і нестандартні рішення, творчо ставитись до праці. Мають високий рівень національної свідомості.
3.5 Фестиваль математики - фестиваль творчості
Здається математика нудна,
І зовсім вже немає в ній краси,
Та тільки зовсім трішки придивись,
І на вершині завжди будеш ти.
За формулою порахуєм час,
Що всіх нас методично поділив,
Когось він опустив, когось підняв,
Ну а когось на фестиваль прислав…
В жовтні місяці впевше відбувся конкурс для обдарованих дітей «Фестиваль математики». У селі Модричі, що на Дрогобичинні, в актовому залі «Нафтуся Прикарпаття» зібралися 9 команд обдарованих дітей Львівщини Команда Сокальської МАН – стала переможцем обласного фестивалю математики та фізики. У впертій боротьбі журі виявило команду, яка найкраще справилася з усіма чотирма раундами математичного туру: «Колектив», «Сума», «Один за всіх…», «Всі за одного…». Журі очолював доктор фізико-математичних наук, професор, директор Інституту фізики, математики, економіки та інноваційних технологій Дрогобицького державного педагогічного університету імені Івана Франка Василь Бойчук.
Розпочинався фестиваль з представлення команд. Ми підійшли до цього завдання творчо, доклали чимало зусиль, щоб лаконічно, видовищно і дотепно розказати глядачам про себе. «Ти тільки розв’язуй ці задачі складні, свою історію ти з ними твори, царицю наук ми прославляєм сповна, бо добре чи зле з тобою завжди вона»,- співали у пісні діти.Уже після першого туру фестивалю лідерство захопила команда нашої Сокальської МАН. Хлопці і дівчата із Сокаля зразу ж набрали відчутну перевагу в балах і від раунду до раунду тільки зміцнювали своє лідерство, незважаючи на достойний опір з боку інших учасників. У підсумку переможцем фестивалю стала наша команда у складі Назарія Бачинського (капітан), Назарія Мачинського, Юлії Мусій, Богдана Барила, Святослава Кунанця та Вікторії Пономаренко. Грамоти та призи переможцям вручили міський голова Дрогобича Тарас Кучма та заступник голови Дрогобицької районної ради Володимир Стецівка.
«Рівняння, логарифми, корені, роблять нас щасливими людьми, олімпіади, фестивалі, зустрічі зможемо подолати тільки ми. Безу нам теорему написав, що б нам відкрити той незнаний світ, чекаєм що прийде такий момент, коли під ноги впаде цілий світ»,- співали щасливі переможці.
Перемога не дається легко. Її передували масове розв’язування тестів, диференційованих завдань, розв’язування задач різними способами, масові репетиції і тренування. Вітер Прикарпаття завіяв у серце обдарованої дитини прекрасну любов до математики – як науки життя. Спогади від такої праці і перемоги вселяють віру у серце дитини і ще є одним кроком на шляху «Через терни до зірок». (додаток 7)
3.6 Науково-практична конференція присвячена пам’яті І.Г Каспрука
Великий талант вимагає великої працьовитості.
Петро Чайковський
Праця з обдарованими дітьми вимагає непосидючості. Я повинна завжди бути в русі, створювати затишні і безпечні умови для розвитку дитини, що вимагає застосування різних форм педагогіки, надання авторитетної допомоги, терпимість до безладдя, здатність до самоаналізу.
Сам час, сьогодення створює дитині умови для конкретного втілення творчої ідеї, надає дитині свободу вибору , заохочення, розвиває цікавість, допитливість, кмітливість, інтелект, формує пізнавальні інтереси, творчий особистий світогляд, виховує культуру мовлення.
В травні місяці, в Сокальській МАН проходить конференція, присвячена пам’яті колишнього директора Івана Григоровича Каспрука . Обдаровані діти мають можливість познайомитися з елітою: сином Івана Григоровича та внуком, і разом з тим поділитися з ними своїми надбаннями. Знову виступи, знову перемоги, знову хвилювання і переживання. Учні показують захопленість математикою, здатністю до експериментальної , наукової і творчої діяльності, широкої інтелектуальності, прагнення до саморозвитку і самоактивації . Відчувається енергійність та індивідуальність дитини, віра у власні сили та самоствердження, творчий стиль діяльності і водночас ще один шлях до зірок.
В силу обставин що скалися, приємно що є люди, яким небайдужі обдаровані діти, доля яких хвилює, за яких переживають і радіють разом з малими науковцями їхнім новим звершенням.
4.1 Робота над собою – запорука успіху.
«Якщо хочеш навчити інших, довго учись сам».
Сучасний вчитель повинен іти в ногу з часом, часом який вимагає глибини знань, наполегливості, орієнтації в нестандартних ситуаціях. Тільки робота над собою, своїми знаннями, діями може допомагати іншим.
Вчитель повинен перебувати в постійному методичному пошуку, якщо прагне зробити процес співпраці з обдарованими учнями творчістю. Саме через це я підвищую свою науково – теоретичну та методичну підготовку шляхом відвідування семінарів, конференцій, роботі в творчій групі вчителів математики, виступів на педрадах і просто величезною працею вдома при підготовці до уроків.
Діти, як ніхто, відчувають фальш. Тим більше – обдаровані особистості. До зустрічі з ними треба наполегливо готуватися, вдосконалювати свою педагогічну майстерність, а саме головне щоб не перетворити дитину в склад знань, комору правил та формул треба вчити її мислити.
Пам’ятаю, що сучасний вчитель повинен старатися, щоб його світогляд став внутрішнім переконанням, брати участь у громадському житті, постійно дбати про підвищення свого культурного рівня. Вчитель повинен бути прикладом працьовитої та наполегливої людини, прикладом бездоганного ставлення до учнів, їх сімей, до людей які нас оточують. Тільки в такому випадку ми можемо розраховувати на успіх і співпрацю з дітьми, пам’ятаючи слова, що педагог повинен володіти максимальним авторитетом і мінімальною владою.
Стараюсь викладати математику так, щоб викликати жвавий інтерес обдарованих дітей, стимулювати їх до пізнання невідомого, розвивати мислення, творчість, формувати вміння, користуватися знаннями в практичному житті.
«Своєчасно знайти, виховати й розвинути задатки і здібності у своїх вихованців, своєчасно розпізнати у кожному його покликання» - першочергове завдання, яке стоїть переді мною в навчально-виховному процесі.
. Античний принцип «Docendo discimus» - навчаючи інших ми вчимося самі, пам’ятаю завжди.
4.2 Особистий приклад учителя в розвитку обдарованої дитини
«Мудрість життя полягає в тому, щоб любити те, що направду є добром. Любити життя і цінувати кожну його хвилину, нести радість, у книгах – шукати істину, у людях – мудрість, виконувати дві основні заповіді Слова Божого: любити Бога всім своїм серцем і ближнього свого, як самого себе.
Бути взірцем, працювати чесно в своєму покликанні».
А. Шептицький
Дітям властиве наслідування вчинків і звичок дорослих та в першу чергу вчителів, тому я повинна бути дуже вимогливою до себе, до своєї поведінки. Повинна бути чесною, справедливою, організованою, разом з тим терплячою, тактовною, чуйною, пам’ятати, що той вчитель добрий чиї слова не розходяться з ділом, котрий не коливається у сказаному.
Складний час переживає наша Україна. Дуже часто потворне підноситься красивим, гріховне – привабливим. Моральність вивертається навиворіт. Смертельно отруйна начинка пропонується у привабливій обгортці. Кажуть, що труднощі загартовують, а моральність оберігає вільну духом людину від спокус. Саме це, кожен з нас, вчителів повинен пам’ятати при роботі з обдарованими дітьми, наповнюючи їх молоду душу відвагою, надією, радістю.
Моїм педагогічним кредом при роботі з творчими особистостями є любов. Я батьківською любов’ю, люблю тих, кого навчаю. Любов – як свічка. Вона несе світло і тепло, вогонь енергії та творення. Ця енергія звернена до дітей. Любов допомагає мені підшукувати правильні слова. Допомагає бути лагідною і ніжною, вимогливою та суровою, дозволяє мені і суворі речі казати з приємністю, працювати з обдарованою особистістю з радістю.
Принцип лікаря «Не зашкодь!» стовідсотково підходить мені, як «лікарю», що формує розвиток душі дитини. Я завжди думаю про наслідки і йду на крок попереду своїх учнів, не забуваючи про моральне прищеплення добра, правди і радості. Подібне прагне до подібного «У сполучених посудинах рівень рідини один»,- казав Паскаль. Шлях від мого серця «живильного джерела» до серця дитини повинен бути коротким і завжди відкритим.
Діти – це саме те, кому я служу всім серцем і всією душею. Заради них, я біжу до школи з радістю. Прагну до різноманіття, пам’ятаючи про свіжість ідей і думок.
Як математик, між словами «дитинство і обдарованість» сміливо ставлю знак рівності, зважаючи на власний досвід. Відшукую дрімаючі особистості, вчу їх любити математику, підбадьорую , відкриваю, веду по шляху «через терне до зірок» , до нових висот.
«Любов довго терпить, любов милосердствує, не заздрить, любов не величається, не поводиться нечемно, не рветься до гніву, не думає лихого, не радіє з неправди, але тішиться правдою, усе зносить, вірить у все, сподівається всього, усе терпить».
Еммануіл Кант казав, що є дві засадничі речі у світі, зоряне небо над головою і моральний закон у середині нас, закон який закликає нас бути чесним у своєму покликанні, вести дитину за руку на складному творчому шляху, допомагати і вчити їх бути переможними.
ВИСНОВКИ:
У нашій долі немає нічого випадкового.Я завдячую саме їй за можливість працювати з дитячим колективом, творчими особистостями.,котрі індивідуальні і неповторні.
Опис мого досвіду роботи з обдарованими дітьми став доведенням ДИВОВИЖНОЇ, ЧУДОВОЇ ТЕОРЕМИ:
«Для того, щоб бути успішним вчителем математики, необхідно і достатньо працювати над собою і просто любити дітей».
Використовуючи аксіому, що є опорним фактом у доведенні, «Любов + усмішка + творча праця = обдарована дитина » веду дітей по тернистому шляху до певних результатів, пам’ятаючи слова великого пастира Андрея Шептицького « Душа дитини- неначе чистий листок паперу…» . Дитина від природи наділена здібностями і обдаруваннями, з неї можна зліпити творчу особистість, здатну на експеримент, дослідження, творчість, головне вірити в її сили, вселяти в неї цю віру.
Працюючи з обдарованими дітьми, я плекаю особистість, яка вміє думати самостійно, досліджувати, експерементувати, вчиться працювати на майбутнє.
Переступаючи поріг школи, я усвідомлюю що прихожу до учнів, щоб розпізнати у кожному з них людську особистість, здатну розвиватись і прогресувати, відшукати обдаровану дитину, допомогти розкрити свої здібності, талант, сформувати активну життєву позицію на благо неньки України.
Як вчитель я люблю дітей, але вважаю, що мудра у своїй любові, підбадьорую дитину в момент помилки, підтримую лад і порядок в дитячому колективі, сприяю кожній дитині йти власним шляхом саморозвитку, долаючи терни науки.
Додаток 1
«Геній може вільно дихати тільки в атмосфері свободи»


Додаток 2
«Геніальність – це всього-навсього незвичний погляд на речі»

Додаток3
Клуб «Едісон» - індивідуальна траєкторія розвитку обдарованого учня




Додаток 5
«Перемога» - результат роботи команди обдарованих дітей на турнірі





Додаток6
Науково-дослідницька робота – шляхетний приклад виявлення обдарованості.




ВІДДІЛ ОСВІТИ СОКАЛЬСЬКОЇ РАЙДЕРЖАДМІНІСТРАЦІЇ
МЕТОДИЧНИЙ КАБІНЕТ
Збірник
завдань з математики
для підготовки до
ІІІ етапу Всеукраїнської олімпіади та конкурсу - захисту
науково –дослідницьких робіт учнів-членів МАН

Укладач : Кровіцька Лариса Ярославівна
Вчитель математики Сокальської загальноосвітньої школиI-III ступенів №4, керівник творчого об’єднання юних математиків Сокальської МАН.
Рецензент :Білик Олеся Іванівна –методист відділу освіти Сокальської райдержадміністраціїї
В збірнику зібрано задачі для підготовки до олімпіади з математики та написання контрольної роботи при захисті науково –дослідницьких робіт (III етап ) та подано їх розв’язки. Посібник розраховано для вчителів при роботі з обдарованими дітьми.
2017 рік
І частина.
У І частині запропоновані 11 тестових завдань. Для кожного тестового завдання з вибором відповіді запропоновано пять варіантів відповідей, з яких тільки одна правильна.
За кожне правильно виконане завдання І частини нараховується 1 бал.
За кожне не правильно виконане завдання І частини нараховується 0 балів.
1. При яких цілих значеннях ![]() значення виразу
значення виразу ![]() є простим числом?
є простим числом?
|
А) -4;-2;0;2. |
Б) -3;1. |
В) 1;2;3;4. |
Г) |
Д) 0;2;4;6. |
Розв’язання.
![]() і для того, щоб добуток був простим числом, треба, щоб один із множників був 1 а бо -1, а другий – просте число.
і для того, щоб добуток був простим числом, треба, щоб один із множників був 1 а бо -1, а другий – просте число.
Відповідь: А) -4;-2;0;2.
2. Знайти значення виразу ![]() , якщо
, якщо ![]() .
.
|
А) |
Б) |
В) |
Г) |
Д) |
Розв’язання.
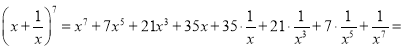
![]() .
.![]()
Тепер, міркуючи аналогічно, виразимо через ![]()
![]() :
:
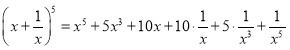
![]() .
.
![]() . Виразимо через
. Виразимо через ![]()
![]() :
:
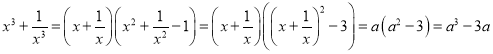 , тому
, тому
![]() ,
, ![]() .
.
Відповідь: Б) ![]() .
.
3. Розв’язати рівняння ![]() .
.
|
А) -6;1 |
Б) -1;6 |
В) -1;1 |
Г) -6;6 |
Д) 0;6 |
Розв’язання. ![]()
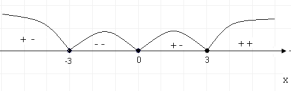
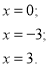
![]()
Відповідь:А) -6; 1.
4. Подати у вигляді звичайного дробу та обчислити: 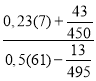 .
.
|
А) 2 |
Б) 7 |
В) 1 |
Г) 23 |
Д) 61 |
Розв’язання. 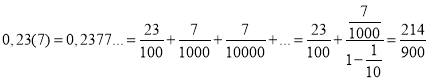 .
.
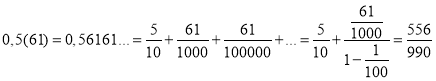 .
. 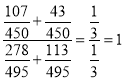 .
.
Відповідь: В) 1.
5. Двоє одночасно пішли від однієї точки у протилежних напрямках берегом озера. Перший проходив щодня 10 миль, а другий пройшов першого дня 1 милю, а кожного наступного дня проходив на 1 милю більше, ніж попереднього. Коли двоє знову зустрілися, виявилося, що перший пройшов ![]() а другий -
а другий - ![]() довжини берега. Скільки днів пройшло до зустрічі?
довжини берега. Скільки днів пройшло до зустрічі? 
|
А) 5 |
Б) 100 |
В) 99 |
Г) 6 |
Д) 11 |
Розв’язання. Позначимо кількість днів до зустрічі через ![]() ,
, ![]() . Тоді перший пішохід пройшов 10
. Тоді перший пішохід пройшов 10![]() миль, а другий
миль, а другий ![]() миль, де
миль, де ![]() сума арифметичної прогресії з першим членом, рівним 1 і різницею1, тобто
сума арифметичної прогресії з першим членом, рівним 1 і різницею1, тобто ![]() миль. За умовою задачі складемо рівняння:
миль. За умовою задачі складемо рівняння:
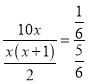 , звідки
, звідки ![]() . Отже, пішоходи зустрінуться через 99 днів.
. Отже, пішоходи зустрінуться через 99 днів.
Відповідь: В) 99 днів.
6. Для яких значень параметра ![]() корені рівняння
корені рівняння ![]() мають різні знаки?
мають різні знаки?
|
А) |
Б) |
В) |
Г) |
Д) |
Розв’язання.
Графіком функції є парабола. Використовуючи графічну ілюстрацію одержуємо умову, за якої корені рівняння мають різні знаки:
![]() . Тоді
. Тоді ![]() . Звідси
. Звідси ![]()
Відповідь: В)![]()
7. Нехай ![]() вершини квадрата (розташовані за рухом годинникової стрілки),
вершини квадрата (розташовані за рухом годинникової стрілки), ![]() -його внутрішня точка, що знаходиться на однаковій відстані від
-його внутрішня точка, що знаходиться на однаковій відстані від ![]() та
та ![]() . Кут
. Кут ![]() дорівнює
дорівнює ![]() . Обчисліть кут
. Обчисліть кут ![]() .
.
|
А) |
Б) |
В) |
Г) |
Д) |
Розв’язання. Нехай ![]() заданий квадрат,
заданий квадрат, ![]() - задана точка, що лежить на серединному перпендикулярі відрізка
- задана точка, що лежить на серединному перпендикулярі відрізка ![]() , тоді
, тоді ![]() , тобто трикутник
, тобто трикутник ![]() - рівнобедрений.
- рівнобедрений. ![]() , отже, трикутник
, отже, трикутник ![]() - рівносторонній. Враховуючи те, що
- рівносторонній. Враховуючи те, що ![]() , отримаємо:
, отримаємо: ![]() , тобто трикутник
, тобто трикутник![]() рівнобедрений. Оскільки
рівнобедрений. Оскільки ![]() , то
, то ![]() .
.
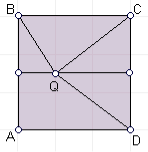 Відповідь: Б)
Відповідь: Б) ![]() .
.
8. На протилежних сторонах ![]() та
та ![]() паралелограма
паралелограма ![]() від вершин
від вершин ![]() і
і ![]() відкладені рівні відрізки
відкладені рівні відрізки ![]() і
і![]() , а на двох інших сторонах – рівні відрізки
, а на двох інших сторонах – рівні відрізки ![]() та
та ![]() . Зясувати вид чотирикутника
. Зясувати вид чотирикутника ![]() .
.
|
А) ромб |
Б) прямокутник |
В) квадрат |
Г) трапеція |
Д) паралелограм |
Розв’язання. Виберемо прямокутну декартову систему координат так, щоб точка ![]() перетину діагоналей паралелограма
перетину діагоналей паралелограма ![]() збігалася з початком координат.
збігалася з початком координат. 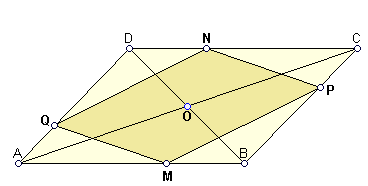 Оскільки протилежні вершини паралелограма
Оскільки протилежні вершини паралелограма ![]() мають координати відповідно
мають координати відповідно ![]() ,
, ![]() ,
, ![]() ,
, ![]() , симетричні відносно точки
, симетричні відносно точки ![]() , то
, то ![]() ,
, ![]() . За умовою задачі
. За умовою задачі ![]() , звідси маємо, що точки
, звідси маємо, що точки ![]() і
і ![]() ділять у певному відношенні сторони
ділять у певному відношенні сторони ![]() і
і ![]() , причому їхні координати:
, причому їхні координати: ![]() ,. А це означає, що точки
,. А це означає, що точки ![]() і
і ![]() - симетричні відносно точки
- симетричні відносно точки ![]() . Аналогічно можна показати, що точки
. Аналогічно можна показати, що точки ![]() і
і ![]() також симетричні відносно точки
також симетричні відносно точки ![]() . Отже. діагоналі
. Отже. діагоналі ![]() і
і ![]() чотирикутника
чотирикутника ![]() точкою перетину діляться навпіл, а це означає. що
точкою перетину діляться навпіл, а це означає. що ![]() - паралелограм.
- паралелограм.
Відповідь: Д) паралелограм.
9. Скільки існує натуральних чисел, у яких кожні дві сусідні цифри утворюють точний квадрат?
|
А) 11 |
Б)12 |
В) 13 |
Г) 14 |
Д) безліч |
Розв’язання. Знайдемо найбільше число, що задовольняє умові задачі та починається з 1 – це число 1649, кожна наступна за 1 цифра знаходиться однозначно. Всі таких чисел, що починаються з 1 – три: 16, 164, 1649. Аналогічно перебором по першій цифрі знаходимо максимальні такі числа, а потім знаходимо їх загальну кількість. З 2 починаються – 25 (1 число); з 3 – 3649, 364, 36 (3 числа); з 4 - 49 (1 число), з 6 – 649, 64 (2 числа); з 8 – 81649, 8164, 816, 81 (4 числа). Разом – 14 чисел.
Відповідь: Г) 14.
10. Знайдіть корені рівняння ![]() , якщо
, якщо![]() .
.
|
А) 1;2;3 |
Б) |
В) |
Г) |
Д) |
Розв’язання.
![]()
![]()
![]()
![]()
![]()
Відповідь: Б) ![]() .
.
11. ![]() та
та ![]() - висоти рівнобедреного трикутника
- висоти рівнобедреного трикутника ![]() з вершиною
з вершиною ![]() . Якою може бути величина кута
. Якою може бути величина кута ![]() , якщо відомо, що
, якщо відомо, що ![]() ?
?
|
А) |
Б) |
В) |
Г) |
Д) |
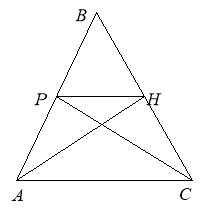
Розв’язання. З того, що трикутник АВС – рівнобедрений: ![]() ||
|| ![]() ,
,
тому трикутники ![]() і
і ![]() подібні з коефіцієнтом подібності 2
подібні з коефіцієнтом подібності 2
(![]() ). Тому
). Тому ![]() . \
. \
Тому ![]() , відповідно й
, відповідно й
![]() або
або ![]() .
.
Відповідь: В) ![]() .
.
ІІ частина.
У ІІ частині запропоновані 4 завдання відкритої форми контролю.
Завдання вважається виконаним правильно, якщо учнем отримана правильна відповідь, наведена логічно правильна послідовність кроків розв’язання.
За кожне правильно виконане завдання ІІ частини нараховується 4 бали.
За кожне не правильно виконане завдання ІІ частини нараховується 0 балів.
12. Знайдіть усі значення виразу ![]() для додатних чисел
для додатних чисел ![]() , які задовольняють систему рівнянь:
, які задовольняють систему рівнянь: 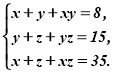
Розв’язання. Якщо додати 1 до кожного рівняння одержимо таку систему: 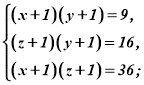
Перемножимо всі рівняння системи: ![]() . Враховуючи, що змінні додатні, одержимо:
. Враховуючи, що змінні додатні, одержимо: ![]() , звідки й знаходимо шукане
, звідки й знаходимо шукане ![]() .
.
Відповідь: 36.
13. Довести, що для будь-яких чисел ![]() та
та ![]() таких, що
таких, що ![]() ;
; ![]() виконується нерівність:
виконується нерівність:
![]() .
.
Доведення.
Використаємо нерівність між середнім арифметичним та середнім геометричним двох чисел:
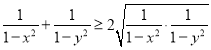 . Тому достатньо довести, що
. Тому достатньо довести, що 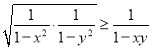 , врахувавши, що
, врахувавши, що ![]() ,
, ![]() , маємо:
, маємо: ![]() , що рівносильно нерівності
, що рівносильно нерівності ![]() .
.
Доведено.
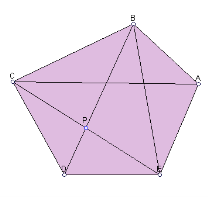 14. Кожна діагональ відтинає від даного опуклого п’ятикутника трикутник, площа якого дорівнює 1. Знайти площу п’ятикутника.
14. Кожна діагональ відтинає від даного опуклого п’ятикутника трикутник, площа якого дорівнює 1. Знайти площу п’ятикутника.
Розв’язання.
За умовою ![]() , тоді
, тоді ![]() . Аналогічно,
. Аналогічно, ![]() ,
, ![]() . Отже,
. Отже, ![]() - паралелограм,
- паралелограм, ![]() ,
, ![]() . Відношення площ трикутників, що мають рівні висоти дорівнює відношенню основ :
. Відношення площ трикутників, що мають рівні висоти дорівнює відношенню основ : ![]() . Позначимо
. Позначимо ![]() . Тоді
. Тоді ![]() ,
, ![]() , бо
, бо ![]() . Шукана площа:
. Шукана площа: ![]() .
.
Відповідь: ![]()
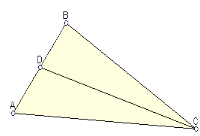 15. В трикутнику
15. В трикутнику ![]() з кута С, градусна міра якого дорівнює 1200 ,проведено бісектрису
з кута С, градусна міра якого дорівнює 1200 ,проведено бісектрису ![]() . Доведіть, що
. Доведіть, що ![]() .
.
Доведення. Площа трикутника ![]() дорівнює сумі площ трикутників
дорівнює сумі площ трикутників ![]() та
та ![]() .
.
![]() ,
,
![]() ,
,
![]() . Тому
. Тому ![]() ,
,
звідки ![]() .
.![]() ,
, ![]() , тому
, тому ![]() рівносильне
рівносильне ![]() , але ж
, але ж ![]() , тому після спрощень, отримаємо рівність 1=1. Доведено.
, тому після спрощень, отримаємо рівність 1=1. Доведено.
ІІІ частина
У ІІІ частині запропоновані 2 завдання відкритої форми з розгорнутою відповіддю, з яких одне з алгебри та одне з геометрії. За кожне правильно розв’язане завдання ІІІ частини нараховується 6 балів. За частково виконане завдання цієї частини можуть бути нараховані 1-5 балів в залежності від кількості правильно виконаних кроків.
16. Розв’яжіть рівняння: ![]() , де
, де ![]() - найбільше ціле число, що не перевищує
- найбільше ціле число, що не перевищує ![]() ;
; ![]() =
=![]() -
-![]() .
.
Розв’язання.
Скористаємось рівністю х=![]() +
+![]() і представимо дане рівняння у вигляді
і представимо дане рівняння у вигляді ![]() , або
, або 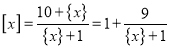 , оскільки
, оскільки ![]() - ціле, а
- ціле, а ![]() ,то число
,то число ![]() - ціле і належить проміжку
- ціле і належить проміжку ![]() .
.
1) Нехай ![]() =5, тоді
=5, тоді ![]() ,
, ![]() =6,
=6, ![]() .
.
2) Нехай ![]() =6, тоді
=6, тоді ![]() .
.
3) Нехай ![]() =7, тоді
=7, тоді ![]() .
.
4) Нехай ![]() =8, тоді
=8, тоді ![]() .
.
5) Нехай ![]() =9, тоді
=9, тоді ![]() .
.
Відповідь:![]()
17. В кут, градусна міра якого дорівнює ![]() , вписано три кола так, що кожне наступне, починаючи з другого, дотикається до попереднього. Знайдіть відношення суми площ усіх трьох кругів до площі найменшого з них.
, вписано три кола так, що кожне наступне, починаючи з другого, дотикається до попереднього. Знайдіть відношення суми площ усіх трьох кругів до площі найменшого з них.
Розв’язання.
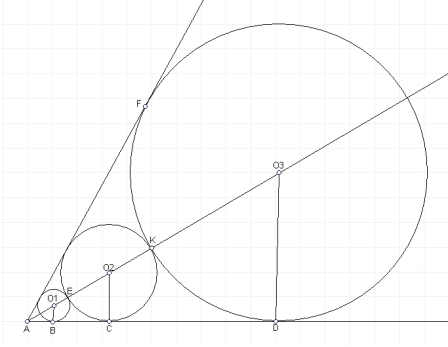 Нехай даний кут -
Нехай даний кут - ![]() .Позначимо радіуси цих кіл за
.Позначимо радіуси цих кіл за ![]() ,
, ![]() ,
,![]() .
.
В прямокутному трикутнику![]()
![]() , тому
, тому ![]() . З подібності прямокутних трикутників
. З подібності прямокутних трикутників ![]() та
та ![]() :
: ![]() ,
, ![]() ,
, ![]() , тому
, тому ![]() .
.
З подібності прямокутних трикутників ![]() та
та ![]() :
: ![]() ,
, ![]() ,
, ![]() , звідки
, звідки ![]() .
.
![]() ,
, ![]() ,
, ![]() - площі трьох кругів, тоді шукане відношення:
- площі трьох кругів, тоді шукане відношення:
![]() =
= 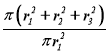 =
= 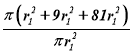 =
= ![]() =
= ![]() . Відповідь:
. Відповідь: ![]() .
.
10 КЛАС
1. Скільки існує натуральних чисел, у яких кожні дві сусідні цифри утворюють точний квадрат?
|
А) 11 |
Б)12 |
В) 13 |
Г) 14 |
Д) безліч |
Розв’язання. Знайдемо найбільше число, що задовольняє умові задачі та починається з 1 – це число 1649, кожна наступна за 1 цифра знаходиться однозначно. Всіх таких чисел, що починаються з 1 – три: 16, 164, 1649. Аналогічно перебором по першій цифрі знаходимо максимальні такі числа, а потім знаходимо їх загальну кількість. З 2 починаються – 25 (1 число); з 3 – 3649, 364, 36 (3 числа); з 4 - 49 (1 число), з 6 – 649, 64 (2 числа); з 8 – 81649, 8164, 816, 81 (4 числа). Разом – 14 чисел.
Відповідь: Г) 14.
2. Продовжить послідовність одним числом: 1,10,100,101,111,1000, 1010,1011,1101,1110,… .
|
А) 1111 |
Б) 10000 |
В) 100000 |
Г) 11111 |
Д) 11110 |
Розв’язання. Якщо помітити, що виписані числа у двійковій системі числення, то їх значення в десятковій дорівнюють: 1,2,4,5,7,8,10,11,13,14… . Як бачимо, пропущені усі числа, кратні 3. Таким чином – нас тупне число – 16, яке в двійковому записі має вигляд 10000.
Відповідь: Б) 10000
3. Двоє одночасно пішли від однієї точки у протилежних напрямках берегом озера. Перший проходив щодня 10 миль, а другий пройшов першого дня 1 милю, а кожного наступного дня проходив на 1 милю більше, ніж попереднього. Коли двоє знову зустрілися, виявилося, що перший пройшов ![]() а другий -
а другий - ![]() довжини берега. Скільки днів пройшло до зустрічі?
довжини берега. Скільки днів пройшло до зустрічі? 
|
А) 5 |
Б) 100 |
В) 99 |
Г) 6 |
Д) 11 |
Розв’язання. Позначимо кількість днів до зустрічі через ![]() ,
, ![]() . Тоді перший пішохід пройшов 10
. Тоді перший пішохід пройшов 10![]() миль, а другий
миль, а другий ![]() миль, де
миль, де ![]() сума арифметичної прогресії з першим членом, рівним 1 і різницею1, тобто
сума арифметичної прогресії з першим членом, рівним 1 і різницею1, тобто ![]() миль. За умовою задачі складемо рівняння:
миль. За умовою задачі складемо рівняння:
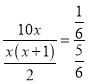 , звідки
, звідки ![]() . Отже, пішоходи зустрінуться через 99 днів.
. Отже, пішоходи зустрінуться через 99 днів.
Відповідь: В) 99 днів.
4. Знайдіть значення виразу ![]() для додатних чисел
для додатних чисел ![]() , які задовольняють систему рівнянь:
, які задовольняють систему рівнянь: 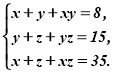
|
А) 35 |
Б) 36 |
В) 136 |
Г) 1649 |
Д) неможливо обчислити |
Розв’язання. Якщо додати 1 до кожного рівняння одержимо таку систему: 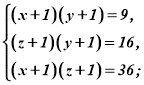
Перемножимо всі рівняння системи: ![]() . Враховуючи, що змінні додатні, одержимо:
. Враховуючи, що змінні додатні, одержимо: ![]() , звідки й знаходимо шукане
, звідки й знаходимо шукане ![]() .
.
Відповідь: Б) 36.
5. Які з чисел ![]() ,
, ![]() ,
, ![]() задовольняють нерівність
задовольняють нерівність ![]() ?
?
|
А) |
Б) |
В) |
Г) |
Д) жодне з чисел не задовольняє нерівність |
Розв’язання. Підстановка ![]() в умову нерівності призводить до правильної нерівності
в умову нерівності призводить до правильної нерівності ![]() ; підстановка
; підстановка ![]() призводить до неправильної нерівності
призводить до неправильної нерівності ![]() ; підстановка
; підстановка ![]() призводить до правильної нерівності
призводить до правильної нерівності 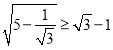 ,
, ![]() .
.
Відповідь: Б) ![]() .
.
6. Знайдіть корені рівняння ![]() , якщо
, якщо![]() .
.
|
А) 1;2;3 |
Б) |
В) |
Г) |
Д) |
Розв’язання.
![]()
![]()
![]()
![]()
![]()
Відповідь: Б) ![]() .
.
7. Яке значення може приймати периметр десятиклітинного многокутника на дошці в клітинку, зі стороною клітинки 1?
|
А) 2,4,6,8,10 |
Б) 1,4,8,12,16 |
В) 11,22,33,44,55 |
Г)11,12,13,14,15 |
Д)14,16,18,20,22 |
Розв’зання. Зрозуміло, що це значення буде парним числом. Максимальний периметр у прямокутника 1х10 і дорівнює 22, мінімальний – у прямокутника 2х5, він складає 14. Інші розв’язки – 16,18,20.
Відповідь: Д) 14,16,18,20,22.
8. В трикутнику![]() на найбільшій стороні
на найбільшій стороні ![]() обирається точка
обирається точка ![]() . Яка найменша відстань між центрами кіл, які описані навколо трикутників
. Яка найменша відстань між центрами кіл, які описані навколо трикутників ![]() та
та ![]() .
.
|
А) 0,5 |
Б) |
В) 0,3 |
Г)1,5 |
Д)2 |
Розв’язання. Нехай ![]() та
та ![]() - центри кіл, що описані навколо трикутників
- центри кіл, що описані навколо трикутників ![]() та
та
![]() відповідно,
відповідно, ![]() та
та ![]() -
-
 середини відрізків
середини відрізків ![]() та
та![]() відповідно. Тоді
відповідно. Тоді ![]() - прямокутна трапеція. В ній
- прямокутна трапеція. В ній ![]() . Знайдемо на стороні
. Знайдемо на стороні ![]() таку точку
таку точку ![]() , для якої виконується рівність
, для якої виконується рівність ![]() . Такою точкою буде основа висоти трикутника
. Такою точкою буде основа висоти трикутника ![]() , проведена з точки
, проведена з точки ![]() (оскільки сторона
(оскільки сторона ![]() найбільша, то така точка належить саме стороні, а не її продовженню). В цьому випадку
найбільша, то така точка належить саме стороні, а не її продовженню). В цьому випадку ![]() і
і ![]() , а чотирикутник
, а чотирикутник ![]() - прямокутник, отже
- прямокутник, отже ![]() .
.
Відповідь: А) 0,5 ![]() .
.
9. Нехай ![]() вершини квадрата (розташовані за рухом годинникової стрілки),
вершини квадрата (розташовані за рухом годинникової стрілки), ![]() -його внутрішня точка, що знаходиться на однаковій відстані від
-його внутрішня точка, що знаходиться на однаковій відстані від ![]() та
та ![]() . Кут
. Кут ![]() дорівнює
дорівнює ![]() . Обчисліть кут
. Обчисліть кут ![]() .
.
|
А) |
Б) |
В) |
Г) |
Д) |

Розв’язання. Нехай ![]() заданий квадрат,
заданий квадрат, ![]() - задана точка, що лежить на серединному перпендикулярі відрізка
- задана точка, що лежить на серединному перпендикулярі відрізка ![]() , тоді
, тоді ![]() , тобто трикутник
, тобто трикутник ![]() - рівнобедрений.
- рівнобедрений. ![]() , отже, трикутник
, отже, трикутник ![]() - рівносторонній. Враховуючи те, що
- рівносторонній. Враховуючи те, що ![]() , отримаємо:
, отримаємо: ![]() , тобто трикутник
, тобто трикутник![]() рівнобедрений. Оскільки
рівнобедрений. Оскільки ![]() , то
, то ![]() .
.
Відповідь: Б) ![]() .
.
10.![]() та
та ![]() - висоти рівнобедреного трикутника
- висоти рівнобедреного трикутника ![]() з вершиною
з вершиною ![]() . Якою може бути величина кута
. Якою може бути величина кута ![]() , якщо відомо, що
, якщо відомо, що ![]() ?
?
|
А) |
Б) |
В) |
Г) |
Д) |

Розв’язання. З того, що трикутник АВС – рівнобедрений:
![]() ||
|| ![]() , тому трикутники
, тому трикутники ![]() і
і ![]() подібні з коефіцієнтом
подібні з коефіцієнтом
подібності 2 (![]() ). Тому
). Тому ![]() .
.
Тому ![]() , відповідно й
, відповідно й
![]() або
або ![]() .
.
Відповідь: В) ![]() .
.
11. Обчислити суму: ![]()
|
А) |
Б) |
В) |
Г) |
Д) |
Розв’язання. Задача зводиться до обчислення суми нескінченної спадної геометричної прогресії, в якій перший член дорівнює ![]() , а знаменник дорівнює
, а знаменник дорівнює ![]() .
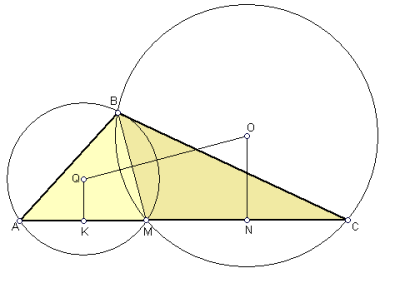
. 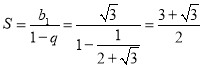 .
.
Відповідь: В) ![]() .
.
ІІ частина.
12. На презентації були запропоновані три зразки товарів А, В і С. Товару виду А купили 112 штук, виду В – 118 штук, виду С – 95 штук. При цьому 68 осіб узяли зразки А і В, 62 особи – зразки В і С, 52 особи – зразки А і С, 38 осіб – взяли усі три зразки, а 13 не купили жодного із запропонованих зразків. а)Скільки осіб купили тільки зразок А, скільки – тільки зразок В і скільки – тільки зразок С? б) Скільки людей відвідали презентацію?
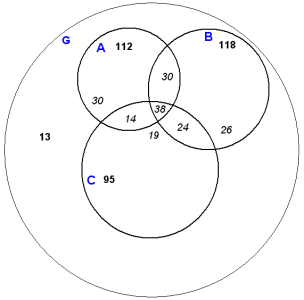 Розв’язання. Позначимо через G множину всіх відвідувачів презентації, через А – множину покупців товару виду А, через В – множину покупців товару виду В, через С – множину покупців товару виду С. Розмістимо числові значення на діаграмі:
Розв’язання. Позначимо через G множину всіх відвідувачів презентації, через А – множину покупців товару виду А, через В – множину покупців товару виду В, через С – множину покупців товару виду С. Розмістимо числові значення на діаграмі: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
а) Тільки зразок А придбали ![]() =
=
![]() . Аналогічно обчислюємо, зразок В купили 26 відвідувачів, а зразок С – 19.
. Аналогічно обчислюємо, зразок В купили 26 відвідувачів, а зразок С – 19.
б) Також з діаграми можна обчислити загальну кількість відвідувачів презентації:
G=112+26+19+24+13=194.
Відповідь: тільки зразок А купили 30 осіб, 26 – тільки В, 19 – тільки С, на презентації було 194 відвідувачі.
13. Розв’яжіть нерівність ![]() .
.
Розв’язання.Нерівність визначена при ![]() . Оскільки
. Оскільки ![]() , то дану нерівність можна переписати так:
, то дану нерівність можна переписати так: ![]() ;
; ![]() .
.
За означенням ![]() , тому
, тому ![]() , звідки
, звідки ![]() ,
,
тобто, ![]() . Найменше ціле значення змінної
. Найменше ціле значення змінної ![]() з цього відрізка дорівнює -1.
з цього відрізка дорівнює -1.
Відповідь: -1.
14. Пряма, паралельна основі трикутника, поділяє його на частини, площі яких відносяться як 2:1, починаючи від вершини. В якому відношенні ця пряма ділить бічні сторони трикутника?
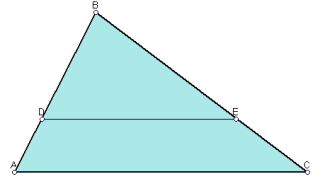 Розв’язання. Якщо позначимо площу
Розв’язання. Якщо позначимо площу ![]() , то
, то ![]() , а
, а ![]() . З подібності трикутників
. З подібності трикутників ![]() та
та![]() маємо:
маємо: 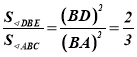 , звідси
, звідси ![]() .
. 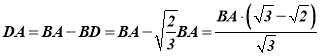 .
.
Тоді ![]() :
: 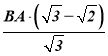 =
=![]() .
.
Отже, відношення, у якому ![]() ділить бічні сторони трикутника дорівнює
ділить бічні сторони трикутника дорівнює![]() .
.
Відповідь: ![]() .
.
15. В коло вписано чотирикутник ![]() , довжини сторін якого дорівнюють
, довжини сторін якого дорівнюють ![]() ,
,![]() ,
,![]() ,
,![]() . Знайдіть відношення довжин діагоналей цього чотирикутника.
. Знайдіть відношення довжин діагоналей цього чотирикутника.
Розв’язання. ![]() ,
,![]() ,
,![]() ,
,![]() . За наслідком з теореми синусів
. За наслідком з теореми синусів ![]() , де
, де ![]() - радіус описаного кола, а
- радіус описаного кола, а ![]() ;
; ![]() , де
, де ![]() .
.
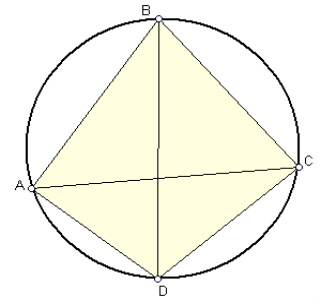 Звідси
Звідси ![]() . З іншого боку,
. З іншого боку, ![]() =
= ![]() , тобто
, тобто ![]() . Тоді
. Тоді ![]() .
.
Відповідь: ![]()
ІІІ частина
У ІІІ частині запропоновані 2 завдання відкритої форми з розгорнутою відповіддю, з яких одне з алгебри та одне з геометрії. За кожне правильно розв’язане завдання ІІІ частини нараховується 6 балів. За частково виконане завдання цієї частини можуть бути нараховані 1-5 балів в залежності від кількості правильно виконаних кроків.
16. Розв’яжіть рівняння ![]() відносно
відносно ![]() .
.
Розв’язання. ОДЗ заданого рівняння: 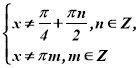 .
.
1) При ![]() одержуємо
одержуємо ![]() ,
, ![]() , тобто
, тобто
![]() -рівність, правильну для будь-яких
-рівність, правильну для будь-яких ![]() .
.
2) ![]() отримуємо рівняння
отримуємо рівняння ![]() , рівносильне рівнянню
, рівносильне рівнянню
![]() , або
, або ![]() .
.
-
Якщо
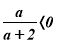 (
(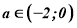 ), то коренів немає.
), то коренів немає.
-
Якщо
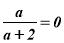 , (
, (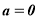 ), то
), то 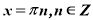 , але ці корені не входять до ОДЗ заданого рівняння.
, але ці корені не входять до ОДЗ заданого рівняння.
-
Якщо
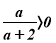 (
( 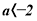 або
або 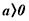 ), то
), то 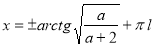 ,
, 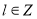 .
.
Відповідь: 1) Якщо ![]() , то
, то ![]() ;
;
2) Якщо ![]() або
або ![]() , то
, то ![]() ,
, ![]() ,
, ![]() .
.
17. Навколо кола радіуса ![]() см описана рівнобічна трапеція, площа якої дорівнює 5 см2. Знайти площу чотирикутника, вершинами якого є точки дотику кола та сторін трапеції.
см описана рівнобічна трапеція, площа якої дорівнює 5 см2. Знайти площу чотирикутника, вершинами якого є точки дотику кола та сторін трапеції.
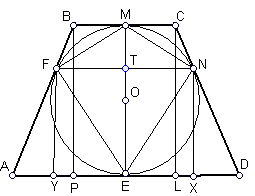 Розв’язання. 1)
Розв’язання. 1) ![]() ,
, ![]() ,
, ![]() ,
, ![]() Опуклий чотирикутник, можна вписати в коло, якщо виконується умова:
Опуклий чотирикутник, можна вписати в коло, якщо виконується умова:
2) ![]() , але
, але![]() , тому і
, тому і ![]() , з умови
, з умови ![]() , значить
, значить ![]()
3) З прямокутного трикутника ![]() маємо
маємо
![]()
4) ![]() - рівнобічна трапеція,
- рівнобічна трапеція, ![]() , тоді
, тоді ![]() .
.
5) Маємо ![]()
![]()
![]() .
.
6) Як відомо ![]() ,
, ![]()
![]()
![]() .
.
7) Звідси ![]() .
.
8) ![]()
Відповідь: 1,6 см2.
11 КЛАС
І частина.
1. Обчислити значення виразу ![]() . Відповідь округлити до цілих.
. Відповідь округлити до цілих.
|
А) 9 |
Б) 10 |
В) 3 |
Г) 2 |
Д) 5 |
Розв’язання.
![]() =
= ![]() =
=![]() =
=![]() =
=
= ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]()
![]() .
.
Відповідь: А) 9.
2.Обчислити числове значення виразу ![]() без таблиць і калькулятора.
без таблиць і калькулятора.
|
А) 49 |
Б) 10 |
В) 36 |
Г) 64 |
Д) 25 |
Розв’язання.
![]() =
= ![]() .
.
1) ![]() ; 2)
; 2) ![]() .
.
Відповідь: Б) 10.
3. Обчислити ![]() .
.
|
А) 0 |
Б) -1 |
В) 1 |
Г) 0,5 |
Д) 2 |
Розв’язання.
![]()
Відповідь: Д) 2.
4. Обчислити значення виразу ![]() .
.
|
А) 3 |
Б) |
В) |
Г) |
Д) |
Розв’язання.
![]() .
.
Відповідь: А) 3.
5. Обчислити значення дробу 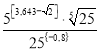 , (де
, (де ![]() - найбільше ціле число, що не перевищує
- найбільше ціле число, що не перевищує ![]() ;
;
![]() =
=![]() -
-![]() ).
).
|
А) |
Б) |
В) 25 |
Г) |
Д) 125 |
Розв’язання.
![]() .
.
Відповідь: В) 25.
6. Розв’язати нерівність ![]() .
.
|
А) |
Б) |
В) |
Г) |
Д) |
Розв’язання.
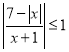 ;
; 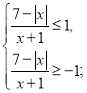
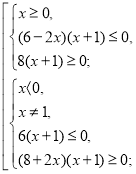
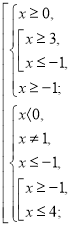
![]()
![]()
Відповідь: В) ![]()
7. Знайдіть найменший період функції ![]() .
.
|
А) 7 |
Б) 3,5 |
В)4 |
Г) |
Д) |
Розв’язання.
Для розвязання задачі достатньо знайти найменший додатній період функції ![]() :
:
![]() .
.
Відповідь: Б)3,5.
8. Нехай ![]() вершини квадрата (розташовані за рухом годинникової стрілки),
вершини квадрата (розташовані за рухом годинникової стрілки), ![]() -його внутрішня точка, що знаходиться на однаковій відстані від
-його внутрішня точка, що знаходиться на однаковій відстані від ![]() та
та ![]() . Кут
. Кут ![]() дорівнює
дорівнює ![]() . Обчисліть кут
. Обчисліть кут ![]() .
.
|
А) |
Б) |
В) |
Г) |
Д) |
 Розв’язання. Нехай
Розв’язання. Нехай ![]() заданий квадрат,
заданий квадрат, ![]() - задана точка, що лежить на серединному перпендикулярі відрізка
- задана точка, що лежить на серединному перпендикулярі відрізка ![]() , тоді
, тоді ![]() , тобто трикутник
, тобто трикутник ![]() - рівнобедрений.
- рівнобедрений. ![]() , отже, трикутник
, отже, трикутник ![]() - рівносторонній. Враховуючи те, що
- рівносторонній. Враховуючи те, що ![]() , отримаємо:
, отримаємо: ![]() , тобто трикутник
, тобто трикутник![]() рівнобедрений. Оскільки
рівнобедрений. Оскільки ![]() , то
, то ![]() .
.
Відповідь: Б) ![]() .
.
9. На протилежних сторонах ![]() та
та ![]() паралелограма
паралелограма ![]() від вершин
від вершин ![]() і
і ![]() відкладені рівні відрізки
відкладені рівні відрізки ![]() і
і![]() , а на двох інших сторонах – рівні відрізки
, а на двох інших сторонах – рівні відрізки ![]() та
та ![]() . Зясувати вид чотирикутника
. Зясувати вид чотирикутника ![]() .
.
|
А) ромб |
Б) прямокутник |
В) квадрат |
Г) трапеція |
Д) паралелограм |
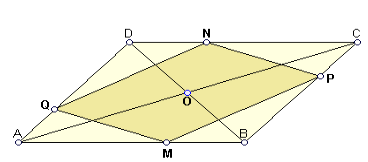 Розв’язання.
Розв’язання. ![]() та
та ![]() (за першою ознакою рівності трикутників), тоді
(за першою ознакою рівності трикутників), тоді ![]() ,
, ![]() і
і ![]()
![]()
![]() - паралелограм.
- паралелограм.
Відповідь: Д) паралелограм
10. Знайдіть об’єм правильної чотирикутної призми якщо її діагональ утворює з площиною бічної гарні кут ![]() , а сторона основи дорівнює
, а сторона основи дорівнює ![]() .
.
|
А) |
Б) |
В) |
Г) |
Д) |
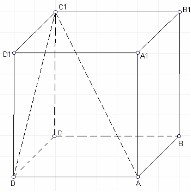 Розв’язання.
Розв’язання. ![]() - проекція
- проекція ![]() на площину
на площину ![]() , тому
, тому ![]() ,
, ![]() . В прямокутному трикутнику
. В прямокутному трикутнику ![]()
![]() , тому
, тому ![]() . Тоді
. Тоді ![]() .
.
З прямокутного ![]() :
: ![]() . Тоді об’єм призми
. Тоді об’єм призми ![]() =
=![]() .
.
Відповідь: Г)![]() .
.
11. При яких значеннях змінних ![]() вектор
вектор ![]() та вектор
та вектор ![]() будуть колінеарними?
будуть колінеарними?
|
А) |
Б) |
В) |
Г) |
Д) |
Розв’язання. Колінеарні вектори мають пропорційні координати, звідси: ![]() ,
, 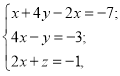
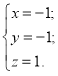
Відповідь: Д) ![]()
ІІ частина.
12. При яких значеннях параметра ![]() функція
функція ![]() зростає на всій числовій прямій (при
зростає на всій числовій прямій (при ![]() )?
)?
Розв’язання.
Запишемо умову задачі у вигляді
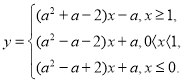
Лінійна функція ![]() зростає при довільному
зростає при довільному ![]() , коли
, коли ![]() . У цьому випадку пряма утворює з віссю
. У цьому випадку пряма утворює з віссю ![]() гострий кут.
гострий кут.
Графік даної функції складається з трьох частин: променів ![]() (
(![]() ) і
) і ![]() (
( ![]() ) та відрізка
) та відрізка ![]() (
(![]() ). Дана функція зростає при довільному
). Дана функція зростає при довільному ![]() , якщо прямі
, якщо прямі ![]() ,
,![]() і
і ![]() нахилені до осі
нахилені до осі ![]() під гострим кутом, тобто, коли виконується система умов:
під гострим кутом, тобто, коли виконується система умов: 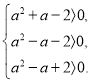 Розв’язавши систему , отримаємо
Розв’язавши систему , отримаємо ![]() .
.
Відповідь: ![]() .
.
13. Розв’яжіть нерівність: ![]() .
.
Розв’язання.
![]() .
.
ОДЗ: 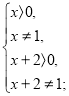
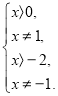
![]()
![]() ,
, ![]() , тому
, тому ![]() ,
, 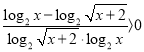 , отримаємо
, отримаємо ![]() , яка на ОДЗ має такі розв’язки:
, яка на ОДЗ має такі розв’язки: ![]() .
.
Відповідь: ![]() .
.
14. Навколо кулі радіуса r описано правильну трикутну піраміду, висота якої дорівнює h. Обчислити об’єм піраміди. При якому значенні h цей об’єм найменший і чому він дорівнює?
Розв’язання.
З подібності трикутників ![]() та
та ![]() (
(![]() отримаємо, що сторона трикутника основи дорівнює
отримаємо, що сторона трикутника основи дорівнює 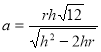 .
. 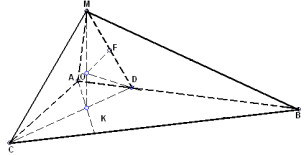 Об’єм піраміди знайдемо за формулою
Об’єм піраміди знайдемо за формулою ![]() ;
; ![]() ;
;
![]() ;
;
![]() .
.
Дослідивши на екстремум функцію ![]() отримаємо, що цей об’єм буде найменшим при
отримаємо, що цей об’єм буде найменшим при ![]() і дорівнюватиме
і дорівнюватиме ![]() .
.
Відповідь: ![]() .
.
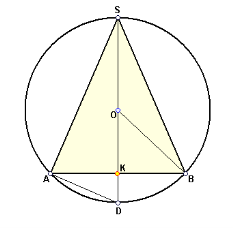 15. Навколо конуса описано кулю радіуса
15. Навколо конуса описано кулю радіуса ![]() . Кут при вершині осьового перерізу конуса дорівнює
. Кут при вершині осьового перерізу конуса дорівнює ![]() . Визначити об’єм конуса, якщо
. Визначити об’єм конуса, якщо ![]() ,
, ![]() .
.
Розв’язання. Розглянемо осьовий переріз конуса. ![]() ,
, ![]() ,
, ![]() ,
, ![]() . З
. З ![]() ,
,![]() . З
. З ![]() ,
, ![]() ,
, ![]() . Тоді
. Тоді ![]()
![]()
![]() .
.
Відповідь: 3,2.
ІІІ частина.
16. Знайти всі прості числа ![]() , для яких вираз
, для яких вираз ![]() є квадратом натурального числа.
є квадратом натурального числа.
Розв’язання. При ![]() маємо, що частка не ціле число, тоді
маємо, що частка не ціле число, тоді ![]() - непарне. Згідно з малою теоремою Ферма,
- непарне. Згідно з малою теоремою Ферма, ![]() ділиться на
ділиться на ![]() . Припустимо, що для деякого натурального числа
. Припустимо, що для деякого натурального числа ![]()
![]() . Оскільки
. Оскільки ![]() - непарне число, то
- непарне число, то 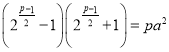 .
.
Обидва множники зліва непарні і взаємно прості між собою. З цього випливає, що лише один із цих множників ділиться без остачі на ![]() . Тому або
. Тому або ![]() або
або ![]() .
.
І. Нехай ![]() ,
, ![]() . Але тоді
. Але тоді ![]() , яке можливе тільки при
, яке можливе тільки при ![]() , тобто при
, тобто при ![]() . Безпосередньою перевіркою переконуємось, що
. Безпосередньою перевіркою переконуємось, що ![]() задовольняє умову задачі.
задовольняє умову задачі.
ІІ. Нехай ![]() ,
, ![]() . Тоді при
. Тоді при ![]() отримаємо, що
отримаємо, що ![]() при діленні на 4 в остачі дає 3, що не можливо. Тому
при діленні на 4 в остачі дає 3, що не можливо. Тому ![]() може бути рівним лише 3. Перевірка показує, що
може бути рівним лише 3. Перевірка показує, що ![]() задовольняє умову задачі.
задовольняє умову задачі.
Отже, лише при простих ![]() і
і ![]() вираз
вираз ![]() є квадратом натурального числа.
є квадратом натурального числа.
Відповідь: 3; 7.
17. Дано кут ![]() і точку
і точку ![]() зовні цього кута. Побудувати пряму, яка проходить через точку
зовні цього кута. Побудувати пряму, яка проходить через точку ![]() , перетинає
, перетинає ![]() в точці
в точці ![]() ,
, ![]() в точці
в точці ![]() таким чином, щоб трикутник
таким чином, щоб трикутник ![]() мав даний периметр
мав даний периметр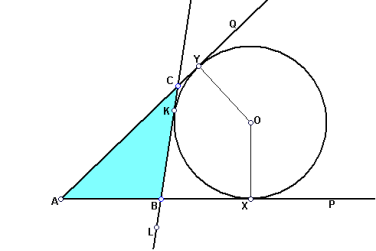
Розв’язання.
Аналіз. Припустимо, трикутник ![]() з даним периметром, наприклад
з даним периметром, наприклад ![]() , побудовано. Розглянемо зовні вписане коло трикутника
, побудовано. Розглянемо зовні вписане коло трикутника ![]() , яке дотикається до сторони
, яке дотикається до сторони ![]() в деякій точці
в деякій точці ![]() , і продовження сторін
, і продовження сторін ![]() і
і ![]() у точках
у точках ![]() і
і ![]() відповідно. Тоді
відповідно. Тоді ![]() , і це коло ми можемо побудувати. Тоді ми можемо побудувати і сам трикутник
, і це коло ми можемо побудувати. Тоді ми можемо побудувати і сам трикутник ![]() .
.
Побудова. Відкладемо на сторонах даного кута відрізки довжиною ![]() і
і ![]() . Будуємо перпендикуляри до сторін кута, що проходять через точки
. Будуємо перпендикуляри до сторін кута, що проходять через точки ![]() та
та ![]() і перетинаються в точці
і перетинаються в точці ![]() . Будуємо коло з центром
. Будуємо коло з центром ![]() радіуса
радіуса ![]() . Проводимо дотичну до цього кола, яка проходить через точку
. Проводимо дотичну до цього кола, яка проходить через точку ![]() і перетинає сторони кута
і перетинає сторони кута ![]() і
і ![]() в точках
в точках ![]() і
і ![]() відповідно.
відповідно.
Доведення. За побудовою шукане коло є зовні вписаним для ![]() ,
, ![]() - точки дотику кола до продовження сторін
- точки дотику кола до продовження сторін ![]() і
і ![]() відповідно. Тоді
відповідно. Тоді ![]() , де
, де ![]() півпериметр
півпериметр ![]() , що й треба було довести.
, що й треба було довести.
Дослідження. Таких дотичних можна побудувати дві, проте, ми обираємо ту з них, яка залишає коло зовні трикутника ![]() .
. ![]() рівні за катетом та гіпотенузою, отже точка
рівні за катетом та гіпотенузою, отже точка ![]() є рівновіддаленою від сторін даного кута, тобто є центром кола з р адіусом
є рівновіддаленою від сторін даного кута, тобто є центром кола з р адіусом ![]() .Трикутник АВС є шуканим.
.Трикутник АВС є шуканим.
Список використаних джерел
1. Бабинская И. Л. Задачи математических олимпиад. – М.: Наука, 1975
2. Валах В. Я. Подорож у світ цілих чисел. – К.: Ррадянська школа, 1978. 3. Гельфонд А. О. Решение уравнений в целых числах. – 4-е издание. – М.: Наука, 1983.
4. Коба В. І , Чуб О.Т., Нікулін М.А. Бесіди про рівняння. – К.: Радянська школа, 1986.
5. У світі математики: Зб. Наук.-попул. статей/ За ред. М. Й. Ядренка. – К.: Радянська школа, 1985. – Вип.16.
6. Федяк І. В. Розв’язування рівнянь. Доведення нерівностей. – Бібліотечка заочної математичної школи. – Тернопіль, 1997.
7. Цыпкин А. Г. Справочник по математике для средней школы. – М
ВІДДІЛ ОСВІТИ СОКАЛЬСЬКОЇ РАЙДЕРЖАДМІНІСТРАЦІЇ
МЕТОДИЧНИЙ КАБІНЕТ
Кровіцька Л.Я.
Методичний посібник
НАУКОВО-ДОСЛІДНИЦЬКА РОБОТА З МАТЕМАТИКИ

Сокаль 2017
к

Зміст
Вступ........................................................................................................................4
- Вибір теми та організація наукового дослідження з математики................5
- Загальна структура наукового дослідження.................................................10
-
Особливості оформлення наукової роботи з математики...........................13
- Ілюстрації....................................................................................................14
- Таблиці........................................................................................................14
- Формули......................................................................................................15
- Правила оформлення бібліографії.................................................................17
- Додатки.............................................................................................................20
Список використаних джерел.................................................................................25

Вступ
„Математика не лише вчить мислити,
а й уселяє віру в безмежні сили людського розуму.
Вона виховує волю, характер”.
Василь Сухомлинський
Не секрет, що математика завжди вважалася і вважається одним із найскладніших предметів, однак не можна переоцінити її особливу роль у розвитку мислення, формуванні обдарованої особистості. Повноцінне навчання математики у сучасному розумінні має за мету не лише отримання дітьми ґрунтовних знань, але й озброєння їх умінням застосовувати знання творчо, нестандартно, постійно поповнювати систему знань; знаходити оригінальні методи, способи, прийоми розв’язування завдань та проблем; критично оцінювати результати власної діяльності. Математична освіта є стратегічним ресурсом розвитку цивілізації, оскільки під час вивчення саме цього предмету закладаються основи для того, щоб школяр у майбутньому став активним, самостійним і відповідальним суб’єктом власної професійної діяльності.
Малу академію наук створено з метою розвитку творчої обдарованості школярів, залучення їх до науково-дослідницької, експериментальної, конструкторської та винахідницької діяльності. Учні, яких не задовольняють знання з шкільного курсу математики, мають змогу брати участь в роботі гуртків та секцій МАН, де навчаються за авторськими інноваційними програмами, поглиблено вивчаючи окремі теми. Підсумком роботи секції є наукове дослідження слухача, яке виростає в науково-дослідницьку роботу. Навички і розвинуті здібності, набуті учнями під час виконання науково-дослідницької роботи, є беззаперечною основою для успішної роботи з написання рефератів, курсових і дипломних робіт у ВНЗ У запропонованому посібнику наведене узагальнення планування та організації наукового дослідження з математики, охарактеризовані вимоги до змісту, структури та оформлення наукової роботи
1. Вибір теми та реалізація наукового дослідження з математики
Відділення математики МАН включає три секції: „Математика”, „Прикладна математика”, „Математичне моделювання”. Тому, вибравши тему наукової роботи, слухач повинен чітко визначити, якому напряму буде відповідати майбутнє дослідження.
Прикладна математика – наука, яка розглядає застосування математичних методів, алгоритмів в інших областях науки і практики. Прикладами такого застосування можуть бути: математична фізика, теорія інформації, теорія ігор, фінансова математика і теорія страхування, теорія ймовірності і статистика, криптографія тощо.
Математичне моделювання – це вивчення явищ або процесів шляхом створення їх математичних моделей та дослідження цих моделей. В основу методу математичного моделювання покладено ідентичність форми рівнянь і однозначність співвідношень між змінними в рівняннях оригіналу і моделей. Математичне моделювання застосовують всі природничі і суспільні науки, що використовують математичний апарат для спрощеного опису реальності за допомогою математичних понять.
Математика – наука, історично заснована на розв’язанні задач про числові і просторові співвідношення реальної дійсності шляхом ідеалізації необхідних для цього властивостей об’єктів і формалізації цих задач. А.М. Колмогоров характеризував математику як науку про числові співвідношення і просторові форми реальної дійсності.
Науково-дослідницька робота починається з вибору теми. Тема – це наукове завдання, яке охоплює певну галузь наукового дослідження. Вона базується на багатьох наукових питаннях – дрібніших наукових завданнях, які належать до конкретної галузі наукового дослідження.
Вибір теми наукового дослідження школярів повинен здійснюватися за такими критеріями: актуальність теми, її новизна, перспективність, ступінь відповідності інтересам та мотиваційній спрямованості слухача МАН. Слід зазначити, що в процесі роботи над дослідженням тема може дещо змінитися: звузитись, конкретизуватися тощо.
Особливо слід звернути увагу на коректне формулювання назви дослідницької роботи. Слід уникати занадто загальних назв, що не відповідають змісту роботи. Наприклад:
|
Неправильно |
Правильно |
|
Комплексні числа |
Комплексні числа та їх геометрична інтерпретація |
|
Рівняння з параметрами |
Розв’язання рівнянь, нерівностей, систем рівнянь з параметрами графічним методом |
|
Метод математичної індукції |
Метод математичної індукції та його використання в теорії подільності |
|
Доведення нерівностей |
Доведення нерівностей методами диференціального числення |
|
Застосування золотого перерізу |
Застосування властивостей золотого перерізу в задачах шкільного курсу математики |
Досить часто учні розпочинають працювати над науково-дослідницькою роботою в 9 чи 10 класі і продовжують в 10 або 11. Відзначимо, що при продовженні наукового дослідження на наступний рік, тема повинна бути змінена так, щоб відображати новизну та вдосконалення цього дослідження порівняно з минулорічним. Наприклад:
|
10 клас |
11 клас |
|
Математичне моделювання гри в теніс |
Математичне моделювання баскетболу, футболу та тенісу |
|
Діафантові рівняння та їх розв’язання |
Діафантові рівняння: дослідження кількості розв’язків кожного окремого рівняння |
|
Оптимізація при плануванні номенклатури продукції підприємств за допомогою ланцюгів Маркова |
Використання ланцюгів Маркова у задачах оптимізації перевезень |
Отож, тему вибрано. Далі слухач самостійно або з допомогою наукового керівника добирає відповідні наукові джерела (книги, брошури, статті) та опрацьовує їх.
Наступний етап – уточнення теми і розробка структури науково-дослідницької роботи. При розробці структури роботи найперше треба обґрунтувати вибір теми, визначити її актуальність, новизну, сформулювати мету дослідження, розробити завдання тощо.
Мета – те, чого потрібно досягти в кінцевому результаті дослідження, вона націлює на здобуття нових знань про предмет, що призведе до підвищення якості об’єкта. Зазвичай, мету починають формулювати так: „...обгрунтувати...”, „...дослідити...”, „...виявити...”, „..виявити можливості використання...” тощо.
Іноді далі формулюється гіпотеза – наукове передбачення, припущення про причини або закономірності будь-яких явищ природи, суспільства чи мислення, достовірність яких ще не доведена дослідним шляхом. Гіпотеза дослідження – це обґрунтоване припущення про можливі способи розв’язання визначеної проблеми, які призведуть до якісної зміни об’єкту дослідження.
Аналіз діяльності учнів під час написання науково-дослідницьких робіт дав можливість визначити, що найбільше часу (понад 50%) витрачається на висунення гіпотези та її обґрунтування. Як відомо, гіпотези потрібні тоді, коли виникає потреба пояснити факти, які не вкладаються у межі відомих раніше наукових теорій чи інших їх пояснень. Висунення гіпотези – одне з головних умінь дослідницької діяльності, адже гіпотеза – той компас, який визначає напрям наукової роботи. Вдало сформульована гіпотеза запобігає невизначеності результату дослідження і спрямовує його на доведення реальності існування передбачуваного припущення.
Висунення гіпотези здійснюється поетапно в такій послідовності:
- висунення попередніх здогадів;
- обґрунтування здогадок, відкидання неприйнятних;
- обґрунтування робочих гіпотез та їх обговорення;
- уточнення й чітке формулювання гіпотези.
Сформульована мета й гіпотеза дослідження логічно визначають завдання, які потрібно вирішити у процесі роботи. Найчастіше вони формулюються так: „...вивчити...”, „виявити...”, „розробити...” тощо. Бажано, щоб відповіддю на поставлені завдання був зміст відповідних розділів роботи.
На наступному етапі проводиться робота з систематизації накопиченого, відповідно до плану роботи, матеріалу, проведення аналізу наукових праць, практичного досвіду, узагальнення тощо.
Згодом необхідно дані, отримані експериментально, обробити статистично. На основі отриманих матеріалів про окремі явища, що вивчаються, визначаються дані, які характеризують досліджуваний комплекс загалом. Зведення результатів дослідження не слід плутати з підведенням підсумків, тобто підсумовування даних, отриманих в результаті дослідження. Зведені результати дослідження підлягають вивченню та аналізу. Головне завдання аналізу наявних даних полягає у їх порівнянні з сформульованою гіпотезою та уточненням її.
Наступним кроком є складання розширеного плану науково-дослідницької роботи відповідно до змісту напрацьованого матеріалу.
На завершальному етапі літературно оформляються результати дослідження. Всі матеріали систематизують, готують до узагальнення та літературного оформлення, формулюються загальні висновки до науково-дослідницької роботи
2. Загальна структура науково-дослідницької роботи з математики.
Наукове дослідження слухача МАН має таку загальну структуру:
Вступ (обґрунтування актуальності теми дослідження, ступеня її вивченості, визначення об’єкта, предмета, гіпотези, мети і завдань, методів дослідження, характеристика його новизни і практичного застосування).
Основна частина (теоретичний аналіз наявних наукових джерел, вивчення стану практики, висвітлення технології дослідження та його результатів). Складність теми та специфіка змісту дослідження визначають кількість його розділів. Типовою є структура, що складається з двох розділів, кожен з яких складається з двох чи трьох параграфів.
Заключна частина (висновки на основі проведеного дослідження, які повинні відповідати поставленим завданням).
Список використаних джерел
Додатки (таблиці, схеми, рисунки тощо)
Проаналізуємо детальніше кожний структурний компонент науково-дослідницької роботи.
Вступ має свою внутрішню структуру:
Актуальність дослідження: (лат. actyalis - дієвість, важливість, своєчасність) обґрунтовується своєчасність, важливість розробки теми для розвитку математичної науки та практики, аналізується ступінь її вивченості в теорії та практиці. Актуальність дослідження – це співвідношення між тим, що вже відомо з цієї проблеми і тим, що буде досліджуватися. При цьому здійснюється короткий огляд теоретичних праць.
Тема дослідження – формулюється на основі вивчення проблеми (суперечності) в науці і практиці.
Об’єкт дослідження – це сукупність елементів об’єктивної реальності, що породжують проблемну ситуацію, і обрано для вивчення та подальшого впровадження.
Предмет дослідження – елемент об’єкту (частина), якісне перетворення якого впливає на вдосконалення (підвищення ефективності, якісне оновлення, зміну) об’єкту дослідження.
Об’єкт та предмет дослідження співвідносяться між собою як загальне і часткове.
Завдання дослідження: намічена програма дослідницьких процесів, яка визначає шлях наукового пошуку. Завдання формулюються згідно з планом дослідження.
Теоретичні основи дослідження: окремі розділи теорії, які покладено в основу дослідження, його науково-теоретична база.
Практична значущість отриманих результатів – визначення ефекту, що спричиняється через практичне застосування результатів дослідження, та зазначення окремих шляхів застосування їх на практиці.
Обсяг вступу – 2-3 сторінки.
Послідовність наукового пошуку слухача відображає зміст роботи (додаток 3). Він містить найменування та номери початкових сторінок всіх розділів, підрозділів та пунктів (якщо вони мають заголовок), зокрема вступу, висновків до розділів, загальних висновків, списку використаних джеред, додатків тощо.
В першому розділі описують результати вивчення наукової літератури та стан реальної практики відповідно до теми дослідження, формують підходи, вплив яких на об’єкт призведе до переходу його у новий, бажаний якісний стан.
В другому розділі характеризують фактор впливу (технологію, способи, засоби, методи, умови) на об’єкт дослідження, доводять його дієвість щодо розв’язання наукової проблеми. Дієвість фактору доводиться в умовах експерименту, хід та методи якого поетапно описуються.
Висновки формулюються на основі систематизації та узагальнення матеріалів наукового пошуку і відповідно до його завдань. Це логічне завершення наукової роботи. Висновки подаються окремими короткими пунктами. Зазвичай, спочатку у висновках оцінюють стан питання, розкривають методи розв’язання поставленої проблеми та узагальнюють результати. У висновках слід підкреслити їх самостійність, новизну, теоретичне або прикладне значення, обґрунтувати достовірність результатів та навести рекомендації щодо їх використання. Висновки не повинні дублювали вступ, основну частину і висновки окремих розділів.
Список використаних джерел формується на основі робочої картотеки. Оскільки змінено вимоги до оформлення літератури, це питання буде розглядатися окремо.
Додатки містять допоміжні або додаткові матеріали, необхідні для повноти сприйняття роботи, кращого розуміння отриманих результатів: допоміжні доведення, формули і розрахунки, таблиці, графіки, рисунки, ілюстрації тощо.
3. Особливості оформлення наукової роботи з математики
Правильне оформлення наукової роботи є одним з показників, які впливають на її загальну оцінку. Важливе значення має змістовний аспект викладу матеріалу (логічність, послідовність, загальна грамотність тощо), правильне оформлення тексту роботи, списку використаних джерел і додатків.
В науковій роботі з математики слід дотримуватися прийнятої термінології, позначень, умовних скорочень і символів. Не допускається виклад матеріалу від першої особи: „Я вважаю”, „На мою думку” тощо. Натомість, коректними будуть формулювання: „Нами було досліджено”, „Ми розв’язали” та ін. Обсяг науково-дослідницької роботи складає 15-20 друкованих сторінок: текстовий редактор Word, шрифт 14, Times New Roman, через 1,5 інтервали, з одного боку білого паперу формату А-4. Поля: ліве – 30 мм; верхнє та нижнє – не менше 20 мм; праве – не менше 10 мм. Всі сторінки, враховуючи додатки, нумеруються. Першою сторінкою вважається титульна, на якій цифра 1 не ставиться (додаток 2).
Науково-дослідницька робота має свою чітко виражену структуру. Основними елементами в порядку розташування є: титульний аркуш, тези (додаток 1), зміст, перелік умовних позначень (за необхідністю), вступ, основна частина, висновки, список використаних джерел, додатки. На наукову роботу обов’язково має бути представлений відгук наукового керівника (додаток 4).
У тезах (обсягом до 1 сторінки) подається стисла характеристика змісту науково-дослідницької роботи з визначенням основної мети, актуальності та завдань наукового дослідження. Також зазначаються висновки та отримані результати.
Специфікою науково-дослідницької роботи з математики є використання формул, малюнків, таблиць. Розглянемо детальніше правила їх оформлення.
3.1. Ілюстрації
Основними видами ілюстративного матеріалу в науковому дослідженні з математики є: креслення, схема, діаграма і графік.
Ілюструвати дослідження потрібно за добре продуманим планом, щоб уникнути ілюстрацій випадкових, пов’язаних з другорядними деталями, і запобігти пропускам ілюстрацій до важливіших тем. Відповідність тексту і ілюстрацій має бути взаємною.
Ілюстрації позначають словом „Рис.”, нумерують двома цифрами, розділеними крапкою. Перша цифра означає номер розділу, друга – номер ілюстрації (наприклад, рис.2.3 – третій рисунок другого розділу). Ілюстрації доповнюють пояснювальними даними (підрисунковий підпис). Посилання на ілюстрації не оформляються як самостійні фрази, в яких повторюється те, що міститься у підписі. В місці, де потрібно вказати на ілюстрацію, розміщують посилання у вигляді виразу в круглих дужках „(рис. 2.1)” або звороту типу: „...як це видно з рис. 2.1”, або”...як це показано на рис. 3.1”, „...як випливає з рис. 3.1”.
3.2.Таблиці
Зазвичай, цифровий матеріал повинен бути оформлений у вигляді таблиці. Над таблицею розміщують її назву, надруковану симетрично до тексту. Назву і слово „Таблиця” розміщують зверху справа із зазначенням її номера. Нумерація таблиць аналогічна до нумерації ілюстрацій (наприклад, Таблиця 1.3 – третя таблиця першого розділу).
Таблицю розміщують після першого згадування про неї в тексті так, щоб її можна було читати без повороту переплетеного блоку роботи або з поворотом за годинниковою стрілкою. Якщо таблиця велика, її можна переносити на наступний аркуш. В такому випадку назву таблиці вміщують лише над її першою частиною. Таблицю з великою кількістю граф можна ділити на частини і розміщувати їх одна над одною на одній сторінці. Якщо рядки або графи таблиці виходять за формат сторінки, то в першому випадку в кожній частині таблиці повторюють її заголовок, а в другому – бокову частину.
Якщо текст, що повторюється в графі таблиці, складається з одного слова, його можна замінити лапками, якщо з двох або більше слів, то при першому повторі вживають слова „Те ж”, а далі – лапки. Однак, ставити лапки замість цифр, знаків, математичних символів, які повторюються, не рекомендовано. В порожніх рядках таблиці ставлять прочерк.
3.3. Формули При використанні в тексті формул слід враховувати певні техніко-орфографічні правила.
Найбільші, а також довгі та громіздкі формули, які містять знаки добутку, суми, диференціювання або інтегрування, розміщують на окремих рядках (нумеровані формули також). Оскільки обсяг науково-дослідницької роботи обмежений (до 20 ст.), то для економії місця кілька невеликих однотипних формул, поданих окремо від тексту, доцільно подати в одному рядку. Нескладні, короткі формули, що не мають самостійного значення, подають всередині рядків тексту.
Пояснення значень символів і числових коефіцієнтів розміщують одразу під формулою в тій послідовності, в якій вони в ній подані. Значення кожного символу і числового коефіцієнта починають з нового рядка, причому перший рядок починається зі слова „де” (двокрапка не ставиться).
Формули і рівняння виділяють з тексту порожніми рядками, не менше одного порожнього рядка вище і нижче формули. Якщо рівняння в один рядок не поміщається, його переносять в наступний після знаку рівності (=), плюс (+), мінус (-), множення (х), ділення (:).
Доцільно нумерувати лише ті формули, на які посилатимуться далі. Для порядкових номерів користуються арабськими цифрами в круглих дужках біля правого берега сторінки без крапки від формули до її номера.
Якщо в роботі використано специфічну термінологію, а також маловідомі скорочення, нові символи, позначення тощо, то їх перелік подається у вигляді окремого списку, який розміщається перед вступом. Цей перелік має розташовуватись двома стовпчиками. Ліворуч в алфавітному порядку наводяться умовні позначення, символи, одиниці скорочення або терміни, праворуч – їх детальна розшифровка.
Додаток1
Зразок оформлення тез наукової роботи
Тези на роботу Бачинського Назарія Петровича на тему
«Елементи сферичної геометрії та її застосування»
Сокальська МАН, 11 клас
Науковий керівник: Кровіцька Лариса Ярославівна
керівник секції математики Сокальської МАН
Сферична геометрія, як і геометрія Евкліда, виникла при вирішенні завдань практичного характеру, і, першочергово, завдань астрономії. Ці завдання були необхідні, наприклад, мандрівникам і мореплавцям, які орієнтувалися за зірками. А оскільки при астрономічних спостереженнях зручно вважати, що і Сонце, і Місяць, і зірки рухаються по уявній «небесній сфері», то природно, що для вивчення їх руху було потрібно знання про геометрію сфери.
Мета дослідження полягає у тому, щоб за допомогою доступних джерел і наукової літератури обґрунтувати використання та застосування елементів сферичної геометрії, показати на практиці використання сферичної тригонометрії.
В результаті дослідження було розглянуто поняття сферичної геометрії,
зокрема сферичної тригонометрії; встановлено певні залежності між планіметрією та сферичною геометрією. В роботі розглянуто також конкретні застосування деяких понять сферичної геометрії в навігації (зокрема спосіб знаходження найкоротшої відстані між двома пунктами вздовж земної поверхні, якщо відомі їх географічні координати; визначення початкового курсу корабля при русі по ортодромії з одного пункту в інший, якщо відомі географічні координати цих пунктів).
В даний час сферична геометрія особливо широке застосування знаходить в астрономії і геодезії (науці про форми і розміри Землі), навігації і картографіях.
Додаток 1
Зразок оформлення титульного листка наукової роботи
Міністерство освіти і науки, молоді та спорту України
Департамент з питань освіти, науки, сім’ї та молоді
Львівської облдержадміністрації
Відділ освіти Сокальської районної державної адміністрації Львівської області
сокальська мала академія наук учнівської молоді
Відділення: математика
Секція: прикладна математика
«ЗОЛОТИЙ ПЕРЕРІЗ» – БОЖЕСТВЕННА ГАРМОНІЯ В НАВКОЛИШНЬОМУ СВІТІ
|
Роботу виконала: Мігус Роксолана Богданівна, учениця 11 класу Сокальської загальноосвітньої школи І – ІІІ ступенів №4»
Науковий керівник: Кровіцька Лариса Ярославівна, керівник секції математики Сокальської МАН
|
Сокаль-2017
Додаток 2
Зразок оформлення змісту наукової роботи
ЗМІСТ
ВСТУП……………………………………………………………………………….3
РОЗДІЛ І. Відношення і пропорції з математичної точки зору………………5
РОЗДІЛ ІІ. Історія виникнення поняття золотого перерізу………………….9
РОЗДІЛ ІІІ. Принцип золотого перерізу – вищий прояв структурної і функціональної досконалості цілого і його частини:
3.1 Золота пропорція в образотворчому мистецтві………………………………12
3.2. Золотий переріз в архітектурі…………………………………………………16
3.3. Золоте відношення у музиці…………………………………………………..20
3.4. Золоті пропорції у літературі…………………………………………………22
3.5 Магічний зміст «золотого перерізу»…………………………………………..24
3.6 Золотий поділ у живій природі………………………………………………..26
3.7 Приклади золотого відношення у людини……………………………………30
3.8 Використання золотого перетину у фотографії………………………………32
РОЗДІЛ IV. Гармонія золотого перерізу і сучасні уявлення про красу……35
ВИСНОВКИ………………………………………………………………………..36
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ……………………………………….38
ВІДГУК
наукового керівника на наукову роботу
„Різницеві рівняння як математичні моделі економічних процесів”
учня 11-А класу Сокальської МАН
Бачинського Назарія Петровича
Перехід до ринкової економіки ставить перед підприємствами низку проблем, пов’язаних із новими для них умовами господарювання, вирішення яких навіть при застосуванні новітніх знань з економіки та комп’ютерної техніки не завжди можливе. Природні економічні експерименти дуже дорогі, часто небезпечні або взагалі не можуть бути реалізовані. В цих випадках і допомагає математичне моделювання. В зв’язку з тим, що багато математичних моделей реальних економічних процесів описуються різницевими рівняннями, обрана тема є актуальною.
Дане наукове дослідження присвячене різницевим рівнянням та їх застосуванню в конкретних економічних задачах. Це дає змогу використовувати роботу як на факультативних уроках математики, так і на уроках економіки. При написання роботи учень виявив вміння систематизувати фактичний матеріал, виділяти головне, показав навики роботи з монографічною літературою.
Вважаю, що із поставленими завданнями учень справився, мета роботи виконана і наукова робота відповідає необхідним вимогам, які ставляться до написання наукових робіт.
Науковий керівник Підпис
Список використаних джерел:
- Богдан С.К. Наукова робота в МАН (методичні рекомендації до її написання й оформлення) / С.К.Богдан. – 3-е вид., доповн. і перероб. – Луцьк, 2009. – 29 с.)
- Крушельницька О.В. Методологія та організація наукових досліджень: Навч. посіб. / О.В.Крушельницька. – К.: Кондор, 2003 – 192 с.
- Цехмістрова Г.С. Основи наукових досліджень: Навч. посіб. / Г.С.Цехмістрова. – Київ: Видавничий Дім „Слово”, 2003. – 240 с.
- Шейко В.М. Організація та методика науково-дослідницької діяльності. Підручник. 3-є видання стереотипне / Шейко В.М., Кушнаренко Н.М. – Київ: Знання-Прес, 2003. – 296 с.
ВІДДІЛ ОСВІТИ СОКАЛЬСЬКОЇ РАЙДЕРЖАДМІНІСТРАЦІЇ
МЕТОДИЧНИЙ КАБІНЕТ
Кровіцька Л.Я.
Методичний посібник
Робота з обдарованими дітьми в рамках проведення тижня математики в школі.

Кровіцька Л.Я. Робота з обдарованими дітьми в рамках проведення тижня математики в школі./ Л.Я. Кровіцька – Сокаль, 2017 – 19 с.
Рецензент: Білик Олеся Іванівна –методист відділу освіти Сокальської райдержадміністраціїї
Посібник містить розробки інноваційних позакласних заходів для роботи з обдарованими дітьми , що проводилися в школі під час предметного тижня. Рекомендовано вчителям математики для проведення предметного тижня, допоможе зробити його цікавим і насиченим.
ЗМІСТ
- Вступ
- Основна частина
- План проведення тижня математики в школі
- Урочиста лінійка присвячена відкриттю тижня математики
І. ВСТУП
Відомо, що робота вчителя – це надзвичайно важка і кропітка праця, яка вимагає високої майстерності, постійного творчого пошуку, наполегливої праці над вдосконаленням педагогічних навичок. Чи цікаво дітям на уроці? Чи люблять вони вчитися? На ці запитання не можна відповісти однозначно. Іноді діти йдуть на урок із задоволенням, іноді без нього. Як зацікавити дітей? Як привернути їхню увагу до навчального предмета?
Часом можна почути, що математика складна, суха і нецікава наука. Людей, які люблять математику це вражає і ображає. Завдання вчителя і полягає в тому, щоб розкривати перед учнями її велич і красу. «Математика – наука, яка вимагає найбільше фантазії, і один з перших математиків нашого століття (Вейєрштрасс) говорить цілком правильно, що не можна бути математиком, не будучи водночас поетом у душі», - писала видатний російський математик Софія Ковалевська.
Кожен учитель прагне зацікавити учнів предметом, який він викладає, бо це є запорукою успішного навчання. Одним із засобів зацікавлення учнів математикою є добре продумана робота з обдарованими дітьми . до яких тягнуться інші. Різноманітні позакласні заходи дають можливість ширше пропагувати досягнення і значення математичної науки, прищепити учням любов до математики, сприяють виявленню і розвитку здібностей учнів, а також глибшому засвоєнню ними програмного матеріалу.
Головне завдання позакласної роботи з математики – виховувати інтерес до математики, розвивати пізнавальні інтереси учнів, стимулювати учнів до вивчення математики. Тому математичні вікторини, змагання, ігри, прес-конференції,вечори сприяють підвищенню математичної культури, розширюють і поглиблюють здобуті на уроках знання, показують застосування їх на практиці, розвивають мислення, математичні здібності, допомагають ввійти у світ наукових і технічних ідей.
Важливий момент цієї роботи полягає також у тому, що для проведення і участі в масових позакласних заходах можна залучати не лише тих учнів, які добре знають математику, а й тих, які на уроках пасивні, але мають артистичні здібності, можуть добре малювати (для випуску математичної газети), і навіть тих, хто зовсім не любить математики. Іноді участь у позакласній роботі стає для таких учнів першим кроком до зацікавленості нею.
II. ОСНОВНА ЧАСТИНА.
Думаємо, що в кожній школі є така традиція – проводити «Тиждень математики», наша школа не є винятком. «Тиждень точних наук» починається з яскравого оголошення, в якому вказано план його проведення. Учнівські стіннівки, випущені спеціально до тижня, вислови відомих людей про математику, а також ребуси, кросворди для учнів кожного класу прикрашають коридори нашої школи. Звичайно, в кожній школі є свої традиції, але, сподіваємося, що когось зацікавить запропонований план проведення цього свята. Можливо, хтось із педагогів – математиків, особливо молодих, які тільки починають працювати в школі, не зовсім чітко уявляють собі, як можна урізноманітнити «Тиждень математики» в школі, тоді цей матеріал стане їм у нагоді.
Які цілі ми ставимо перед собою плануючи математичний тиждень? По-перше, надати учням можливість здобути додаткові знання з математики, історії її розвитку; показати зв'язок математики з іншими науками; по-друге, забезпечити різнобічний розвиток особистості; дати можливість кожному школяру прийняти безпосередню участь у заходах тижня; по-третє, формувати інтерес до вивчення предмета, спонукати учня до пізнавальної діяльності.
«Зацікавити розум дитини – ось що є одним з основних положень нашої доктрини. І ми нічим не нехтуємо, щоб прищепити учневі смак, ми б сказали, навіть пристрасть до навчання» - писав видатний російський математик
М.В. Остроградський.
Щоб спонукати учня до навчання, треба розвивати в ньому потребу займатися пізнавальною діяльністю, а це означає, що в самому процесі навчання він повинен знаходити привабливі риси, щоб сама робота по здобуттю знань містила позитивні заряди зацікавленості. Шлях до цього пролягає через різноманітну самостійну роботу учнів і створення ігрових нестандартних ситуацій. Прикладом саме такої самостійної роботи учнів, проявом їхньої фантазії та абсолютно нестандартного підходу є створення фільму «Математика у вашому житті».
Чимало форм позакласної роботи з математики вміщують елементи гри, і, навпаки, деякі форми позакласної роботи можуть бути частиною математичної гри. Захоплені грою, діти не помічають, що навчаються: пізнають, запам’ятовують нове, розвивають творчу уяву. Навіть найбільш пасивні учні включаються в гру з величезним бажанням. Математичні ігри об'єднують вчення і гру, працю і відпочинок. Вони розвивають математичні здібності,кмітливість, логічне мислення, зміцнюють пам'ять. Використання програмного матеріалу викликає у школярів активізацію розумової діяльності, сприяє виникненню особистих мотивів навчання. А включення завдань, які містять нові для учнів відомості з різних галузей математики, розвиває інтерес і допитливість.
Дуже важливим є той факт, що математична гра поєднує ігрову, навчальну й трудову діяльність. Крім того, така гра вимагає від школяра знання предмета, адже не вміючи розв’язувати задачі, учень не зможе брати участь у грі. В іграх учні вчаться планувати роботу, оцінювати результати діяльності не тільки товаришів, а й своєї, проявляти кмітливість, творчо підходити до виконання будь-якого завдання. Але правила гри повинні бути такими, щоб учні виявили бажання брати в ній участь. Тому ігри слід розробляти з урахуванням вікових особливостей дітей, їхнього загального розвитку й наявних знань.
Сьогодні великою популярністю користуються ігри, які є аналогами телевізійних програм, саме тому під час проведення тижня природничих наук в нашій школі для учнів сьомих класів проводиться математичний квест «Пошук скарбів», але залучені до неї учні всіх класів. Добираючи завдання для конкурсів, вікторин та математичних ігор, дотримуємося думки, що ці завдання не повинні бути складними, вони повинні розв’язуватися усно, без зайвих обчислень на аркуші, але бути водночас й цікавими. Крім того, вважаємо, що на будь – якому позакласному заході учні повинні пізнати щось нове, досі невідоме для них.
План проведення тижня математики в школі
Понеділок (13 березня)
1.Урочисте відкриття тижня математики (лінійка)
2. Конференція для старшокласників "Відомі українські математики": 10- 11 класи(Кровіцька Л.Я.,Опацька А. І.)
3. Конкурс –гра «Я знаю математику на 12» 5 клас Кровіцька Л. Я.
4 «Інформатика і сучасність»-уроки цікавих фактів(Коцюбяк К. Ю. Федюк Л.Б.)
Вівторок(14 березня)
1.Урок цікавих експериментів з фізики 9 клас Гаврилюк В.В.
2. Конкурс малюнків математик
(Кровіцька Л.Я.,Федюк О.Р.) 5 клас
3. «Кульова блискавка » урок – захист НДР Корній М.М. 10 клас
4. Позакласний захід з інформатики ( Федюк Л.Б. )
Середа(15 березня)
1.Математичний турнір веселих і кмітливих Федюк О. Р. 6 клас ( 2 урок)
2. Вікторина для учнів «Математичний олімп» Винниченко Р.М. 6 –В клас 1 урок
3. Інтелектуально- розважальна гра «Наодинці з математикою»Винниченко Р. М.7-А, В клас 7 урок
4. Квест «Пошук скарбів» Кровіцька Л.Я. 7 клас
Четвер(16 березня)
1.Урочиста лінійка .присвячена тижню математики для молодших школярів.
2. Конкурс «КЕНГУРУ -2016»для учнів 2-11 класів
П’ятниця(17 березня)
- Подання учнівських презентацій на тему «Історія математики. фізики , інформатики», «В світі сучасної математики». 5- 11 класи
2.Конкурс математичних, фізичних . інформатичних газет
3. Підведення підсумків тижня математики.
Нагородження учасників
1.Урочиста лінійка присвячена відкриттю тижня математики ( звучить пісня на мелодію Михайла Хоми).
Школа, школа рідний дім
Всім так весело у нім
Йдем знання ми здобувать логарифми «підкорять
Математик я чи ні?
Раз приснився сон мені
Знаю множення на п’ять
Вмію добре рахувать.
Я тепер крутий чувак з математики- мастак
В мене світла голова –математико моя.
Як Ньютон сиджу в саду
Всі уроки тільки й жду
Щоб та швидкість помогла
І добіг він до кінця
А тяжіння діє так
Що я з фізики мастак
До роботи й справи я
Рідна фізико моя.
Я тепер крутий чувак бо я з фізики- мастак
Лопіталь я №2 люба фізико моя.
Я з компютером на ти
Бо ми з ним наче брати
В тій програмі волочем як по полю із м’ячем
У контакти як зайдем
Сам Паскаль туди прийде
В друзі проситься щодня бо я-світла голова.
Я тепер крутий чувак з математики- мастак
Лопіталь я №2 інформатико моя.
Любі друзі!!! Вже багато років коридорами і класами нашої школи впевнено крокує тиждень математики. Всі її любителі, з великим нетерпінням чекали цього дня. І ось він настав.
Запрошуємо вас у цікаву подорож на математичному всюдиході, у чарівну країну - Математику. Протягом цього тижня ми будемо мандрувати її нескінченними просторами, знайомитись з її великими вміннями і надбаннями. Вирушаємо в путь! Нас чудові речі ждуть. Тиждень математики оголошується відкритим.
Цей тиждень будемо ми з вами
Математику вітати
І прекрасній цій науці Віват ,віват співати
Вона вартує всіх похвал
Бо точна скрізь і всюди
За чесність . правду,простоту
Шанують її люди.
Математико царице як без тебе жити
У сучасному світі без тебе кроку не можна ступити.
В магазині.в полі, в школі
Скрізь вона вирує
За задачі про життя її народ цінує.
Один за всіх і всі за одного
Девіз нас кличе у дорогу
Без математики ми ні туди ,а ні сюди
Пам’ятаймо цю істину строгу.
Бо математика – це розум і краса
В ній істина ведеться
Про її велич і могутність
Щоденно пісня ллється.
Хтось скаже що наука ця черства
Лиш цифри, приклади , задачі
А що робить . як настрою нема
І серце від образи тихо плаче.
Довірся їй і все лихе пройде.
І сум твій,як туман минеться
І стане сонячним похмурий день
Це так вона до тебе посміхнеться.
Така вона цариця всіх наук.
Шляхетна . мудра. Добра і весела
Іі корона сонячно іскриться
У кожній школі.у містах і селах.
Ми з нею завжди і серця співають
Ми з нею і сумління наше чисте
Тож хай немов прогресії зростають
Ряди геометрів та алгебраїстів.
О математика
Без неї не ступиш ні кроку
Без неї як в суш без води
Її неповторні уроки в серцях наших будуть завжди..
Пісня про математику (Здається математика нудна…)
Якось зібралися всі науки разом, і почали сперечатися хто з них найголовніший і найважливіший.
- Я найважливіша, бо я вивчаю минуле — сказала Історія.
- Ні, я найважливіша, бо я вивчаю розташування морів і океанів, гір і рівнин, боліт і пустель —сказала Географія.
- Ой ні подруги, найважливіша наука це я, бо вивчаю атоми й молекули, рух, прискорення, швидкість, час, відстань, опір і масу — сказала Фізика.
Тим часом осторонь від них стояла Математика, і чекала доки її подруги скінчать суперечку.
- Ні подруго, Історіє, без чисел не можна буде визначити коли відбулася якась подія
- Ой Географіє, важко ж буде тобі вважатися наукою, коли не буде мене, адже не можна буде розрахувати ні масштабів, ні координат
- А з тобою, Фізико, ми найкращі подруги, адже обидві використовуємо: і формули, і терміни, і правила, але одразу зрозуміло, що без розрахунків і ти не можеш вважатися наукою (цариця математика)
Я визнана давно главою всіх наук –
Потрібна вам я скрізь, завжди і всюди.Без математики ми нині, як без рук.
Зі мною з казки дійсність творять люди.Освоївши мене – рветесь у політ.
Створили вже розумні ви машини,Штурмуєте космічний світ
І різних фактів визнаєте причиниЗі мною ви невпинно ростете,
Зі мною – підкоряєте природу.Зі мною ви щасливі й живете
На благо українського народу
Ще в глибоку давнину люди були впевнені, що числа – це таємний код, за допомогою якого можна зрозуміти пристрій нашого світу. Тисячі років минуло з тих пір, а сучасні вчені не тільки розділяють думку наших предків, але й не перестають доводити, що математика – цариця наук. У музиці, в тарілці, в стихії Числами можна висловити все, що є в нашому світі. Але що ми самі знаємо про цю таємничу і одночасно самої точної науки?
Математика – цариця наук. Хто сказав цю фразу? Ми точно знаємо, як називаються числа і в якому порядку вони слідують один за одним. Але чи часто ми замислюємося над тим, звідки взялися цифри, чому вони виглядають так, а не інакше? Чому саме вони стали головним інструментом математики.
«Математика – цариця наук, а арифметика – цариця математики» - це слова відомого німецького математика Карла Гаусса. Історія математики починається приблизно з того моменту, як наші предки усвідомили, що кількість горщиків і мисливського інвентарю вимагають обліку. Так з'явилися прообрази чисел і сама перша математична операція – складання.
Потреба в математичних розрахунках зростала з кожним днем. Треба було вміти точно підраховувати не тільки кількість людей у своїй громаді, але і поголів'я худоби і площі пасовищ. З бурхливим розвитком торгівлі і будівництва володіння елементарною математикою стало і зовсім запорукою благополуччя. Щоб вижити і прогодувати сім'ю, люди повинні були вміти рахувати. Та й правда, математика - цариця наук, а арифметику – це те, з чого почалася ця наука і без чого не може існувати.
Кожному з нас подобається гармонійна музика. Вона викликає приємні емоції, допомагає розслабитися, може підняти настрій. Але тільки завдяки майстерності музиканта? Виявляється, за гармонійним поєднанням звуків варто математика. Цариця наук розпорядилася так, що дві ноти, розділені таким музичним інтервалом, як октава, чудово звучать разом. Це ідеальне поєднання в музиці. Октава – це співвідношення частот між звуками, які математично можна записати як 1/2. А чиста квінта – 3/2 велика терція – 5/4. Втім, будь-яка комбінація нот записується звичайної математичною пропорцією. Про зв'язок музики і математики здогадалися ще в античні часи, а першим до цього додумався Піфагор.
«Музика - таємна арифметика душі, яка не знає, що обчислює», - якось підмітив відомий філософ і математик Лейбніц. Універсальність математики не перестає дивувати. Здається, що сила цієї науки взагалі безмежна. Математично можна розрахувати навіть природні катаклізми.
Ведучий: Математика - це мова плюс міркування. Це мова й логіка разом. Математика - це знаряддя для міркування. Математика - найекономніша в словах. Вона може обійтися навіть зовсім без слів. Не існують для неї мовні перешкоди, бо її мова, як мова музики, зрозуміла для всіх людей світу.
Ведуча: Про математику, її особливості, її невичерпну красу, можна розповідати без кінця. Любов до неї не виникає відразу. Минають довгі роки напруженої праці, безсонні ночі, світлі надії часом змінюються розчаруванням, поки математика нарешті стає близькою і рідною.
Пам'ятайте! Математика – це наука молодих. Інакше й бути не може. Заняття математикою – це така гімнастика розуму, для якої потрібна вся гнучкість і витривалість молодості.
Ведуча: Хто в дитинстві займається математикою, той розвиває увагу, тренує мозок, волю, виховує в собі наполегливість і завзятість у досягненні мети.
Ведучий: Діапазон практичного застосування математики величезний! Яку б науку ви не вивчали, яку б професію не обрали, всюди обов'язково потрібні математичні знання.
Математика – це розум і краса
В ній істина ведеться
Про її велич і могутність
Щоденно пісня ллється. (пісня)
Квест «Я знаю математику на 12»
Перше завдання: «Знайдіть невідоме число» - це номер наступного кабінету, до завдання додається карта, яка вказує, де саме в кабінеті слід шукати.
22 ,42,51.53,54,4.!8
Наступне завдання лежить на вказаній парті - його необхідно знайти серед речей учнів, які сидять на вказаному місці.
«До номера предмета, якому немає пари додайте три, отриманий результат – це номер вашого наступного кабінету. Знайдіть те, чого там бути не повинно – всередині знаходиться наступна загадка».
«Знайдіть загальну кількість тих, хто плаває, тих, хто порхає та тих, хто дуже любить мед і ви дізнаєтеся, в якому кабінету шукати наступну задачку. На єдиному столі ви її знайдете».
На столі вчителя лежить конверт із пазлом всередині, склавши який команда дізнається куди рушити далі.
На дошці в кабінеті учасники гри знайдуть своє наступне завдання, відповідь до якого вкаже під якою партою прихований номер наступного кабінету.
Біля входу в цю класну кімнату учасники гри побачать своє наступне завдання
«Відгадайте номер кубика – він підкаже на якому ряду знаходиться наступна задачка».
«Запишіть правильний час арабськими цифрами, знайдіть добуток першої і третьої цифр, до результату додайте другу цифру – ви отримаєте номер вашого наступного кабінету».
Це кабінет 7-В, школярі приготували семикласникам загадку, відгадавши яку учасники гри дізнаються де саме шукати своє завдання.
Кількість парусників, це число – шифр, назвавши його четверокласникам, команда отримує в руки вказівку де шукати.
|
Спортзал |
|
|
Нарешті останнє завдання і буде відгадане місце, де заховано скарб.
«Знайдіть зайве на кожному з малюнків, із отриманих результатів за допомогою шифрувальної таблички складіть слово – це і є ваш останній пункт вашого маршруту. Шукайте скарб!»
І ось, нарешті втомлені учасники гри дісталися кінця маршруту, переможці знайшли скарб, дві інші команди отримали солодкі призи. Математичний квест «Пошук скарбів» завершився, всі отримали незабутні враження і позитивні емоції!
Дуже показовим та значущим є той факт, що після проведення такої гри учні усіх паралелей проявляють бажання взяти участь у ній, шестикласники ж чекають свого сьомого класу, щоб обов’язково знайти свій скарб під час математичного тижня.
ГРАміж командами «Послідовники Піфагора» і «Послідовники Вієта»
1) Домашнє завдання
(Представники від кожної команди розповідають біографії Піфагора і Вієта,показуючи портрети видатних математиків.)
2) Конкурс-змагання»Чи знаєте ви?»
- 15 балів-це найвища кількість балів за повідомлення «Чи знаєте ви?»
Команда»Послідовники Вієта»
Чи знаєте ви,що…
…Сергій Микитович Мергелян одержав звання доктора математичних наук, коли йому було 21 рік?
…Михайло Юрійович Лермонтов дуже любив математику і в подорож завжди брав книгу з математики?
…Софія Василівна Ковалевська була в дні Паризької комуни в осадженому Парижі?
…у стародавній Русі число мільйон називалося тьма?
…Отто Юлійович Шмідт,видатний радянський математик, був дослідником Арктики?
… Лейбніц ввів багато математичних термінів,які посідають важливе місце в сучасній науці?
…дробові числа були відомі в Єгипті ще 4000 років тому?
…римляни користувалися дробами із знаменником 12,які називали унціями?
…знаки»більше» і»менше» ввів Геродот?
…першу математичну книгу було надруковано в Росії?
Команда«Послідовники Піфагора»
…Іоганн Кеплер запропонував ставити кому після цілих у десяткових дробах?
…Еваріст Галуа - геніальний французький математик,був убитий на дуелі у 21 рік?
…Архімед був не тільки видатним математиком,а ще й спеціалізувався на механіці,фізиці,астрономії?
…Карлу Гауссу математика замінила звичайні дитячі ігри?
…Софія Василівна Ковалевська з 15 років почала вивчати вищу математику?
…Лейбніц був одночасно філософом і лінгвістом,істориком і біологом?
…Микола Лобачевський у 22 роки викладав в університеті?
…цікавий спосіб складання таблиці простих чисел запропонував Ератосфен
3) Гра «Найрозумніший»
- Хто відповість на більшу кількість запитань за 2 хвилини-той переможець. За правильну відповідь-1бал.
-
Запитання команді послідовників Піфагора
1.Сума двох натуральних чисел дорівнює їх добутку.
2.На яке число потрібно розділити 3,щоб одержати 6.
3.У скільки разів кілометр більший за міліметр?
4.Сота частина числа називається…
5.Результат множення.
6.Рівність двох відношень.
7.Предметом цієї науки є вивчення рівнянь.
8.Протилежні додатним числам.
9.Третій степінь числа.
10.Найменше просте число.
Запитання команді послідовників Вієта
1.Сума яких двох натуральних чисел більша ніж їх добуток?
2.Коли ділене і частка дорівнюють один одному?
3.Скільки кілометрів у мільйоні міліметрів?
4.Результат ділення.
5.Частка від ділення одного числа на інше.
6.Сума одночленів.
7.Рівняння,які мають однакові корені.
8.Частина прямої,обмежена з одного кінця.
9.Найменше натуральне число.
10.Другий степінь числа.
3) Заморочки із бочки.
(Капітани виймають по-черзі номери запитань. На обдумування одного запитання 15 сек. Правильна відповідь-1бал.)
1.Чи може сума трьох послідовних простих чисел бути простим числом?
2.Половина від половини числа дорівнює половині. Яке це число?
3.В одній сім'ї два батька і два сина. Скільки осіб у сім'ї?
4.Чому дорівнює добуток послідовних цілих чисел,які починаються з -5 і закінчуються 5?
5.Твердження,яке потрібно довести.
6.Твердженя,яке не треба доводити.
7.24 години називаються… .
8.Одне яйце варять 4 хвилини. Скільки хвилин потрібно варити 5 яєць?
9.Скільки буде десятків,якщо два десятки помножити на три десятки?
10.2/3 числа дорівнюють 8/5 його. Яке це число?
4) «Відповідь по черзі»
Ведучий читає запитання. За 2 хвилини капітани команд повинні відповісти на найбільшу кількість запитань. Капітани вибирають конверт,з якого беруть запитання
5) Запитання з червоного конверта
1.Він буває гострим,тупим,ним наказують у дитинстві.
2.Відрізок,який перетинає пряму під прямим кутом.
3.Сума суміжних кутів.
4.Сума довжин сторін чотирикутника.
5.Цілі числа,які діляться на два.
6.Чому дорівнює площа квадрата зі стороною 2 метри?
7.Які числа упродовж багатьох віків називалися «абсурдними», «фіктивними»?
8.Для чого використовують решето Ератосфена?
9.Наука про фігури та їх властивості.
10.Найбіль поширена одиниця вимірювання плоских кутів.
6) Запитання із зеленого конверта
1.Пряма,яка обмежена з обох кінців.
2.Чому дорівнює сторона квадрата із периметром 10 метрів?
3.Промінь,який ділить кут навпіл.
4.Прилад для вимірювання кутів.
5.Математичне поняття,яке в перекладі з грецької означає «пишу» і нічого спільного не має з аристократами.
6.Він є в рослинах і в словах,у рівнянні теж він є,і стержневий і кубічний.
7.Дія,обернена до множення.
8.Натуральне число,яке має лише один дільник.
9.Уперекладі з грецької означає «гідна поваги».
10.Вони бувають мисливські,барабанні,а ще десяткові і звичайні.
7) Гра «поле чудес»
|
|
|
|
|
|
|
|
- Чиї це слова: «Людина нагадує дріб,де чисельник-гідність людини, знаменник - самооцінка. Збільшити свій чисельник,тобто збільшити власну гідність,не під силу людині,але будь-хто може зменшити свій знаменник,власну думку про себе,і цим наблизитися до досконалості».
(Толстой)
|
|
|
|
|
|
|
|
- Хто вперше ввів поняття «ФУНКЦІЯ»?
(Лейбніц)
Не залишаємо поза увагою наймолодших учнів середньої школи – п’ятикласників, тому для них математична гра-вікторина.
Розподіл на команди: учасники по черзі обирають номер команди, за яку буде виступати. Команди вчитель формує заздалегідь неофіційно: кількість учнів різних рівнів в кожній команді повинно бути приблизно однаковим, це досягається таким чином: наприклад, готуються фішки 4 кольорів (т. я. 4 рівні), на яких написаний номер команди, а вчитель учневі пропонує вибрати фішку певної категорії (кольору). Кожна команда обирає капітана.
Перший тур – «логічний». Кожна команда отримує завдання. Завдання капітани витягують із загальної купи. Час виконання –
2 хв Правильна відповідь – 1 бал.
1. Бабка (стрекоза) з байки Крилова півдоби спала, третю частину - танцювала, шосту частину – співала. Час, що залишився вона вирішила присвятити підготовці до зими. Скільки часу Бабка готовилася до зими? (24-12-8-4=0)
2. Маса заповненого молоком бідона - 7 кг, а наповненого наполовину –
4 кг. Скільки важить бідон? (1 кг)
3. Чи може бути в якомусь місяці року 5 понеділків і 5 четвергів? (ні)
4. Малюк може з’їсти 600 гр. варення за 6 хвилин, а Карлсон – у двічі швидше. За який час вони з’їдять це варення разом? (за 2 хв.)
Другий тур – «міркувальний». Команди обирають номер запитання. Якщо відповідь правильна з першого разу – 3 б, якщо з другого – 2 б, якщо з третього – 1б.
1
Їх виплачують в банках
Говорять, що більше за 30 – грабіж!
Пишеться начебто 0 ділять на 0
Відсотки
2
Цим стріляють з рушниці
Його вистукують на барабані
Дріб
3
Вона потрібна, щоб не говорити дурниць
Коли одне слідує з іншого
Буває математична, буває жіноча
Логіка
4
Зазвичай знаходиться в центрі міста
Виражається числом в квадраті
Довжина на ширину
ПлощА
Третій тур – «літературний» для капітанів. Вставити слова, яких не вистачає в приказках, які є числівниками. Капітани обирають приказки за їх номерами. Правильна відповідь – 1 бал.
1. … на одного не чекають (7)
2. …раз виміряй, …раз відріж (7, 1)
3. За…зайцями поженешся, не спіймаєш ні… (2,1)
4. У ледачого Омелі … п’ятниць на тижні (7)
Четвертий тур – «економічний». Команди розв’язують задачі економічного змісту. Розв’язана до кінця задача – 5 балів. Час – 5 хв.
1. Лисиця купила у бджіл 100 кг меду за 1000 грн., а на ринку продавала його по 12 грн за 1 кг. Який дохід отримає лиса, коли продасть весь мед? (200 грн.)
2. Скільки необхідно кахельної плитки квадратної форми із стороною
15см для обкладання стіни прямокутної форми розміром 3м × 2,7м? (81000см2/225см2=360 шт.)
3. Ви поклали у банк 50 000 грн. під 10% річних. Якщо через півроку ви захочете забрати всі гроші, то суму ви отримаєте? (52 500 грн.)
4. Бізнесмен поклав в банк 1 000 000 грн. через рік він забрав 1 500 000 грн. Скільки % складає прибуток? (50%)
В цей час гра з болільниками і гостями. «Відгадай загадку»
1. Один учень писав про себе: «...Пальців у мене двадцять п'ять на одній руці, стільки ж на другій, на ногах десять...». Чому він такий потворний?
[ Відповідь ] Учень після слова «двадцять» не поставив дві крапки.
2. Швачка має кусок сукна 18м і щодня відрізає по 3м. На який день вона відріже останній раз?
[ Відповідь ] На п'ятий.
3. П'ять копачів за 5 годин викопують 5м канави. Скільки копачів за 100 годин викопають 100м канави?
[ Відповідь ] 5 копачів.
П’ятий тур «Подільність чисел»
1. Скільки дільників має число 3?
А) один;
Б) два;
В) жодного;
Г) безліч.
2. І на 10 і на 5 діляться натуральні числа, які закінчуються на…
А) 10;
Б) 5;
В) 2;
Г) 0.
3. Найменше просте число.
А) 0;
Б) 1;
В) 2;
Г) 10.
4. Найбільший спільний дільник чисел 18 і 24.
А) 3;
Б) 2;
В) 72;
Г) 6.
5. Число 741 ділиться на…
А) 2;
Б) 3;
В) 9;
Г) інша відповідь.
6. Яку цифру треба дописати до числа 53, щоб воно ділилось і на 3, і на 9?
А) 0;
Б) 2;
В) 4;
Г) 1.
Шостий тур «Історія математики»
1. Одного всесвітньо відомого вченого спитали, як на його думку, з'являються винаходи, що перевертають світ? "Дуже просто,- сказав він.
- Всі знають, що зробити це неможливо. Серед них трапляється один дивак, котрий цього не знає. Він і робить винахід.«Хто цей вчений?»
А) Фалес;
Б) Ньютон;
В) Піфагор;
Г) Енштейн
2. Таблицю простих чисел склав давньогрецький учений…
А) Евклід;
Б) Піфагор;
В) Ератосфен;
Г) Аристотель.
3. Хто з наведених жінок є вченим-математиком?
А) Надія Крупська;
Б) Софія Ковалевська;
В) Валентина Терешкова;
Г) Нонна Мордюкова.
4. Давньогрецький математик і механік Архімед народився у 287 році
до нашої ери і прожив 75 років. У якому році він помер?
А) у 212 році до нашої ери;
Б) у 62 році нашої ери;
В) у 162 році нашої ери;
Г) у 362році до нашої ери.
III. ВИСНОВКИ.
Тиждень математики в нашій школі проводиться з метою формування учбової мотивації з математики, активізації позаурочної діяльності по предмету, розкриття потенціалу вчителя, величезної ролі математики в сучасному світі.
Насамкінець, хотілося б перелічити ті цілі, які нам вдалося досягти при проведенні щорічного тижня математики в нашій школі:
- розвиток пізнавальному інтересу та творчої активності учнів
- використання активних форм демонстрацій своїх досягнень з математики
- виховання потреби в самостійному здобутті знань з математики
- розширення та підтримка кола учнів, які цікавляться математикою
- підготовка учнів до професійної орієнтації.
Отже, проведення предметних тижнів дозволяють внести цікаві заходи та інноваційні технології до навчального процесу, вдосконалити організаційні якості вчителів, розширити світогляд учнів, розвинути їхні творчі здібності, самостійність, естетичний смак. Після проведення предметних тижнів в школярів активізується пізнавальна діяльність, зростає інтерес до вивчення предметів. Насамкінець хотілося б нагадати, що розробляючи заходи для проведення тижня математики, варто пам’ятати:
1. заходи мають переважно особливості змагання, сплановані таким чином, що дають можливість виявити не тільки математичні здібності учнів;
2. учні беруть активну участь у підготовці й проведенні всіх заходів;
3. усі заходи мають бути масовими( залучені якомога більшу кількість учнів).
Лінійка , присвячена закриттю тижня математики.
1-й ведучий Є наука, що розум приводить
У порядок ясний і чіткий,
Нам вона теореми доводить,
Що поєднують формул рядки.
2-й ведучий Математику всі ви впізнали,
Від людей всіх їй честь і хвала,
Також всім, хто її підкоряли,
Промовляєм подяки слова.
2-й ведучий Скільки ще теорем невідкритих
І задач нерозв’язаних є!
Хай живе математика в світі
І для розуму думки дає!
1-й ведучий. Ми живемо в 3 тисячолітті! В час визначних відкриттів і досягнень людства. Ми багато що знаємо, багато що уміємо. Нам відомий вислів старогрецького математика, філософа, що жив у VI ст. до н.е. – Піфагора – «Все є число». Значить, як у минулому, так і в майбутньому, без математики не обійтися.
. Звучить музика, і здається, що може бути спільного між математикою і музикою, між сухими формулами і божественними звуками? А виявляється, є. Ви замислювалися коли-небудь над тим, що за предмет – математика? Ось, наприклад, що вивчає астрономія?
1-й ведучий. Зірки.
2-й ведучий. Вони реально існують?
1-й ведучий. Так.
2-й ведучий. Що вивчає біологія?
1-й ведучий. Навколишній нас світ тварин, рослин.
2-й ведучий. Вони реально існують?
1-й ведучий. Так.
2-й ведучий. Що ж вивчає математика?
1-й ведучий. Числа. Геометричні форми.
2 Ведучий. Вони реально існують? До них можна доторкнутися?
1-й ведучий. Ні.
2-й ведучий. Значить, математика займається речами, яких насправді немає?!
1-й ведучий. Значить, це наука, існуюча тільки в людських думках. Наука, створена розумом людини. І здається чимось надприродним, бо за допомогою формул можна розрахувати , «економічну ситуацію» в країні, погоду «на завтра», описати звучання нот в мелодії.
2-й ведучий. „Предмет "математика" на стільки серйозний, що корисно не упускати випадку зробити його трохи цікавим", - писав видатний учений XVII століття Паскаль. І хоча математика здається багато чим серйозною, і навіть нудною наукою, іноді і в ній прослизає пустотлива усмішка
1-й ведучий Всім знайомі такі імена видатних вчених, як: Архімед, Піфагор, Аристотель, Галілео Галілей, Ньютон, Евклід. Вони принесли великий вклад у розвиток алгебри, геометрії, фізики, астрономії.
2-й ведучий Геометрія — одна з найдавніших наук.— розділ математики, наука про просторові форми, відносини і їхні узагальнення.
1-й ведучий Алгебра — розділ математики, що вивчає властивості дій над різноманітними величинами і розв'язки рівняннь, повязаних з цими діями. Вивчення властивостей композицій різного виду в 19 столітті призвело до думки, що основне завдання алгебри — вивчення властивостей операцій незалежно від об'єктів, до яких вони застосовуються
2-й ведучий Фізика — природнича наука, яка досліджує загальні властивості матерії та явищ у ній, а також виявляє загальні закони, які керують 3 цими явищами; це наука про закономірності Природи в широкому сенсі цього слова.
1-й ведучий Астрономія – (наука про рух і властивості небесних тіл — є однією з найдавніших природничих наук
Інформатика – наука про інформацію.
2-й ведучий Не тільки руки, ноги і тіло вимагає тренування, але мозок людини вимагає вправ. Рішення задач, головоломок, математичних ребусів, розвиває логічне мислення, швидкість реакції. Недаремно говорять, що математика - гімнастика розуму. Так давайте цього тижня ще більше займемося математикою.
1-й ведучий. кожний з вас може перевірити свою увагу, пам'ять, уміння логічно мислити. Хотілося б, щоб після тижня математики , фізики і інформатики ви інакше подивилися на ці науки , , відчули її красу і більш глибоко усвідомили необхідність їх вивчення.
Тим, хто вчив математику, інформатику , фізику
Тим, хто вчить математику, інформатику , фізику
Тим, хто буде вчити
Тим, хто ще не знає,
Що може любити ці предмети
Разом Математичний тиждень присвячується!
1

про публікацію авторської розробки
Додати розробку





