Науково-дослідницька робота " Про примхливість Великої теореми Ферма"
Робота виконана за вимогами МАН. Зміст: тези, вступ, три розділи основної частини, заключення та висновки. Даний матеріал систематизований, узагальнений, доступний для широкого кола. Можна використовувати для інтегрованих заходів в школі. А також може стати в нагоді під час написання наукової роботи , Бажаю творчих успіхів колегам.
ТЕЗИ
до роботи « Про примхливість Великої теореми Ферма »
Актуальність роботи обумовлена використанням алгебраїчних рівнянь, розв’язками яких є цілі числа, їхньою важливістю для суто теоретичних досліджень у пошуках доведення справедливості Великої теореми Ферма.
Використовуючи матеріал з наукової літератури та з Інтернету, було знайдено чимало цікавих історичних фактів про спроби доведення, примхи та підступність самої теореми. Значущими фігурами в історії теореми є відомі вчені П’єр Ферма, Ютака Таніяма, Ендрю Уайлс.
Акцент в роботі зроблено на перевірку та переконання в справедливості твердження , що рівняння виду ![]() при n
при n![]() не мають розв’язків серед натуральних чисел. Проведено самостійні дослідження справедливості твердження у випадку n=3, застосований метод від супротивного. Досліджуючи рівняння у окремих випадках можна визначити два способи: метод перетворень, метод розкладання на множники. При розкладанні на множники достатньо ,щоб права частина рівняння була цілим числом.
не мають розв’язків серед натуральних чисел. Проведено самостійні дослідження справедливості твердження у випадку n=3, застосований метод від супротивного. Досліджуючи рівняння у окремих випадках можна визначити два способи: метод перетворень, метод розкладання на множники. При розкладанні на множники достатньо ,щоб права частина рівняння була цілим числом.
Робота містить три розділи основної частини: історія теореми Ферма, доведення справедливості теореми Ферма, популяризація теореми через художні твори. Також наведені приклади застосування теореми у випадку n=2.
Запропонована анотація до літературних творів, в яких йдеться про теорему Ферма.
Даний матеріал систематизований, узагальнений, доступний для широкого кола. Можна використовувати для проведення інтегрованих заходів в школі.
ЗМІСТ
ТЕЗИ………………………………………………………………………….2
ВСТУП ……………………………………………………………………….4
РОЗДІЛ 1……………………………………………………………………..6
ПРИМХИ ДОЛІ ВЕЛИКОЇ ТЕОРЕМИ ФЕРМА
1.1. П'єр Ферма………………………………………………………………6
1.2. Теорема, непокірна та приваблива протягом трьох століть …………6
1.3. Ендрю Уайлс………………………………………………………….. .8
РОЗДІЛ 2…………………………………………………………………….9
ДОВЕДЕННЯ СПРАВЕДЛИВОСТІ ТЕОРЕМИ ФЕРМА
2.1.Обґрунтування теореми Ферма…………………………………………9
2.2. Геометрична інтерпретація теореми Ферма…………………………..9
РОЗДІЛ 3……………………………………………………………………13
ТЕОРЕМА ФЕРМА В ЛІТЕРАТУРІ ТА МИСТЕЦТВІ
3.1. Сюжетна лінія про теорему Ферма в літературних творах…………13
3.2. Згадки про теорему Ферма в кіномистецтві, мистецтві……………..14
ЗАКЛЮЧЕННЯ……………………………………………………………..15
ВИСНОВОК…………………………………………………………………18
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ…………………………………..20
ВСТУП
На канікулах я прочитала роман Стіга Ларссона «Дівчина, яка грала з вогнем». В ньому йдеться про складність та неможливістьрозв’язання Великої теореми Ферма. Мене зацікавив даний факт. Отже, я ввела в пошуковик «Теорема Ферма», і знайшла безліч статей про життя і діяльність П’єра Ферма, про суперечливі і загадкові гіпотези та докази його теорії.Сподіваюсь, що ця інформація буде цікавою моїм одноліткам.
У XX столітті сталася подія, рівної за масштабом якої в математиці не було за всю історію. 19 вересня 1994 була доведена теорема, сформульована П'єром де Ферма в 1637 році. Вона відома також як «Велика теорема Ферма». Її довів 41- річний професор Прінстонського університету Ендрю Уайлс. Рем Мерті дав оцінку актуальності популяризації доведення Уайлса теореми Ферма: «Велика теорема Ферма займає особливе місце в історії цивілізації. Своєю зовнішньою простотою вона завжди притягувала до себе як любителів, так і професіоналів.»![]()
Дослідницьку роботу вважаю актуальною, тому що наукових статей, присвячених Великій теоремі Ферма забагато, але в широкому сенсі (в доступній формі) недостатньо. Спеціальної обробки інформації щодо інтеграції теореми в мистецтво немає.
Об’єктом дослідження є примхлива історія доведення Великої теореми Ферма .
Предметом розгляду даної теми є ключові спроби доведення істинності твердження Ферма та популяризація теореми засобами культури та мистецтва .
Мета роботи полягає в з’ясуванні справедливості Великої теореми Ферма, наведенні прикладів застосування теореми за шкільною програмою, а також обробки літературних джерел за обраною темою.
Я поставила собі завдання про можливість доступного викладу доведення та усвідомлення істинності теореми. По-перше, дізнатися про історію доведення. По-друге, з’ясувати нові математичні поняття з теми. По-третє, вивчити методи доведення теорем. Я спробую переконати та довести істинність теореми Ферма. А також, я поставила завдання вивчити літературні твори, в сюжетній лінії яких простежується Велика теорема Ферма. Стиль роботи має полегшити сприймання та осмислення теореми. Я спробую скласти відповідні анотації до художніх творів, в яких йдеться про теорему Ферма.
Відповідно до поставленої мети та завдань робота складається зі вступу, трьох розділів, заключення, висновків та списку використаних джерел.
У процесі дослідження було використано інтернет-ресурси, окремі наукові видання, бібліографічні джерела.
Робота носить інформаційно-теоретичний характер. Матеріали даної роботи можна використовувати при підготовці до математичних турнірів , при проведенні математичних чи інтегрованих позаурочних заходів, при проведенні квестів серед старшокласників.
Отже, дана робота присвячена історії Великої теоремі Ферма .
РОЗДІЛ 1.
ПРИМХИ ДОЛІ ВЕЛИКОЇ ТЕОРЕМИ ФЕРМА
- П'єр Ферма
П'єр Ферма (1601-1665) народився на півдні Франції в містечку Бомон-де-Ломань. Метричний запис про його хрещення від 20 серпня 1601 року говорить: "П'єр, син Домініка Ферма, буржуа і другого консула міста Бомона".![]() У коледжі П'єр придбав добре знання мов: латинської, грецької, іспанської, італійської. Ферма славився як тонкий знавець античності.
У коледжі П'єр придбав добре знання мов: латинської, грецької, іспанської, італійської. Ферма славився як тонкий знавець античності.
Велика заслуга Ферма полягає в тому, що його наукові роботи сприяли розвитку нових галузей в математиці: математичного аналізу, аналітичної геометрії, теорії ймовірностей. Багато уваги Ферма також приділяв і питанню про магічні квадрати. Ферма розповсюдив ідею складання магічних квадратів на простір, тобто поставив питання про складання кубів, що володіють властивостями, аналогічними властивостям магічних квадратів.
Самим суперечливим та знаковим стало його твердження, « що для будь-якого натурального числа ![]() (при n > 2) не має рішень в цілих ненульових числах»
(при n > 2) не має рішень в цілих ненульових числах» ![]()
- Теорема, непокірна та приваблива протягом трьох століть
Справедливість теореми Ферма підтверджується для багатьох окремих випадків. Навколо привабливої своєю уявною простотою підступної теореми завжди кипіли неабиякі пристрасті. Історія її доведення - суцільні драми, містика і навіть безпосередні жертви.
У 1907 році в місті Дармштадті в Німеччині помер математик Вольфскель, який заповідав 100000 марок тому, хто дасть повне доведення теореми. Сотні і тисячі людей, стали бомбардувати наукові товариства своїми рукописами, в яких нібито доведено теорему Ферма. Але премія ця до цих пір нікому не видана за відсутністю справжнього доведення Великий теореми .
Випадок, коли n = 3, був доведений Ейлером ще в 1768 році. Але теорія, якою користувався Ейлер при своєму доказі, була доведена Гауссом.
Доказ теореми Ферма для випадку, коли n = 5, запропонували в 1825 році майже одночасно Лежен Дирихле і Лежандр. Своє доведення Дирихле опублікував в 1828 році, але воно було дуже складним, і в 1912 році його спростив Племель.
Для наступного простого показника n = 7 теорема Ферма була доведена лише в 1839 році Ламі, та майже відразу ж доведення вдосконалено Лебегом.
У 1847 році Ламі оголосив, що йому вдалося знайти доведення Великої теореми Ферма для всіх простих показників n ![]() 3. Метод Ламі ґрунтувався на арифметичних властивостях чисел. Однак, Лиувилль виявив в міркуваннях Ламі серйозний пробіл, чим спростував цей доказ.
3. Метод Ламі ґрунтувався на арифметичних властивостях чисел. Однак, Лиувилль виявив в міркуваннях Ламі серйозний пробіл, чим спростував цей доказ.
Ернст Куммер довів, що теорема справедлива для всіх простих n![]() 100, за можливим винятком простих 37, 59, 67.
100, за можливим винятком простих 37, 59, 67.
Мабуть, сама знакова жертва - Ютака Таніяма. У 1955 році 28-річний японський математик Ютака Таніяма висунув твердження із зовсім іншої області математики, що одержало назву "гіпотези Таніями". Твердження випередило свій час. «Кожній еліптичній кривій відповідає певна модулярная форма». ![]() Гіпотеза Таніями поєднала абсолютно різні поняття - досить прості плоскі криві і неймовірні чотиривимірні форми. Саме це стало основою для доведення теореми ( рис.1.1).
Гіпотеза Таніями поєднала абсолютно різні поняття - досить прості плоскі криві і неймовірні чотиривимірні форми. Саме це стало основою для доведення теореми ( рис.1.1).
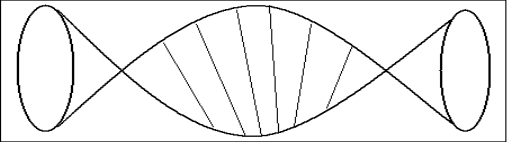 Рис.1.1
Рис.1.1
А через три роки, Ютака Таніяма покінчив життя самогубством. Гіпотеза осиротіла. Ніхто не знав, як її довести.
Минуло приблизно 25 років. У 1985 році німець Герхард Фрей висунув цікаве твердження, схоже на теорему: "Якщо буде доведена гіпотеза Таніями, то буде доведена і Велика теорема Ферма". Іншими словами, теорема Ферма є наслідком гіпотези Таніями. Фрей методом математичних перетворень звів рівняння Ферма до виду рівняння еліптичної кривої:![]()
![]() Але, далі довести його не зміг. А у 1986 р. професор каліфорнійського університету Кеннет Рібет чітко довів теорему Фрея. Минуло ще 8 років. І, здається, Ендрю Уайлс (США) знайшов доказ гіпотези Таніями.
Але, далі довести його не зміг. А у 1986 р. професор каліфорнійського університету Кеннет Рібет чітко довів теорему Фрея. Минуло ще 8 років. І, здається, Ендрю Уайлс (США) знайшов доказ гіпотези Таніями.
1.3. Ендрю Уайлс ЕндрюУайлс, народився в Англії в 1953 році, навчався на математичному факультеті в Кембриджі. Після закінчення аспірантури Уайлс отримав посаду в Прінстонському університеті, де працює і зараз.
Ендрю мріяв довести теорему Ферма вже з юнацьких років. Рухаючись до своєї мети, Ендрю починає спеціалізуватися в сучасній теорії чисел. В результаті семирічного відлюдництва від математичного співтовариства, довгих перевірок і тяжких роздумів, Уайлс нарешті в 1993 році на математичній конференції з теорії чисел в Кембриджі оголосив про своє велике досягнення.
Це, звичайно, була справжня сенсація. Все вирішили, що сталася масштабна подія: доведена гіпотеза Таніями, а отже і Велика теорема Ферма. Але…В доказі було виявлено невідповідність. Тоді Ендрю скористався теорією Івасава, і через рік у в доведенні все зійшлося.![]() Влітку 1995 року в журналі "Аннали математики" було опубліковано повний доказ гіпотези Таніями (отже, Великої теореми Ферма), понад 100 листів. Таким чином, в кінці ХХ століття весь світ визнав, що на 360 році свого життя Велика теорема Ферма, яка насправді весь цей час була гіпотезою, стала доведеною теоремою. Ендрю Уайлс довів Велику теорему Ферма та увійшов в історію. На даний час справедливість Великої теореми перевірена для всіх показників n < 5500.
Влітку 1995 року в журналі "Аннали математики" було опубліковано повний доказ гіпотези Таніями (отже, Великої теореми Ферма), понад 100 листів. Таким чином, в кінці ХХ століття весь світ визнав, що на 360 році свого життя Велика теорема Ферма, яка насправді весь цей час була гіпотезою, стала доведеною теоремою. Ендрю Уайлс довів Велику теорему Ферма та увійшов в історію. На даний час справедливість Великої теореми перевірена для всіх показників n < 5500.
РОЗДІЛ 2
ДОВЕДЕННЯ СПРАВЕДЛИВОСТІ ГІПОТЕЗИ ФЕРМА
- Обґрунтування «Теореми Ферма»
Дана теорема пов'язана з рівнянням![]() .
.
Велика теорема Ферма стверджує, що при значеннях параметра n, що перевищують двійку, цілочислених рішень (x,y,z) даного рівняння не існує (крім випадку, коли всі ці змінні дорівнюють нулю одночасно)![]()
Сам Ферма «довів свою теорему», написавши на полях перекладу «Арифметики» Діофанта: «Тим часом, абсолютно неможливо розкласти повний куб на суму кубів, четвертий степінь - на суму четвертих степенів, взагалі який-небудь степінь - на суму степенів з тим же показником. Я знайшов справді дивовижний доказ цього припущення, але тут занадто мало місця, щоб його помістити ».![]()
Пізніше Ферма опублікував доведення для випадку n = 4, що дає підстави для сумнівів, чи було у нього доведення для загального випадку.
2.2. Геометрична інтерпретація теореми Ферма
Довести треба наступне: Немає цілих a, b, c, для яких при n>2 виконується формул![]() (2.1)
(2.1)
Доведення
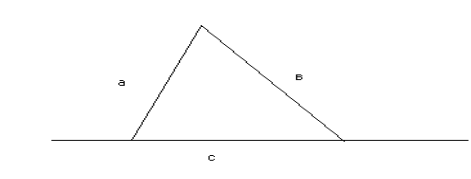 Рис.2.1
Рис.2.1
Зобразимо трикутник. Такий трикутник гострокутний, тобто кожен кут, при перетині двох сторін гострий, ця властивість виконується для будь-якого довільного трикутника, який відповідає формулі (2.1). Припустимо, що сторона c задана деяким сталим числом, а сторони a і b змінюються. Досить довести, що при цілої c, немає двох цілих a і b.
Ми можемо накреслити незліченну кількість трикутників, основою яких служить сторона c, і які задовольняють умові. При цьому геометричним місцем вершин таких трикутників буде служити крива, схожа на еліпс (рис.2.2).
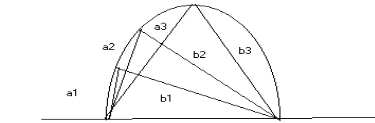 Рис.2.2
Рис.2.2
с
На рис. 2.3 зображені можливі трикутники, симетричні відносно прямої c. Отримана фігура є паралелограмом. Позначимо діагоналі паралелограма С і D, сторони паралелограма В і А.
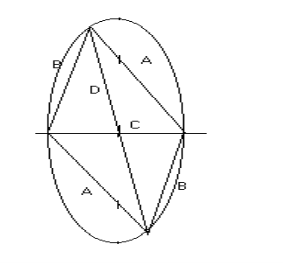 Рис.2.3
Рис.2.3
Вся множина рішень нашого рівняння буде знаходитись в області, яка обмежена кутом повороту діагоналі D, по відношенню до діагоналі С, від 00 до 900. І вершини нашого паралелограма при цьому ковзають по еліпсу. Приходимо до висновку, що для двох однакових і складених дзеркальним чином трикутників, які підкоряються рівнянню![]() виконується властивість чотирикутника:
виконується властивість чотирикутника:![]() ,де С і D - діагоналі , a і b - сторони. Ми бачимо, що змінюються сторони при зміненні діагоналі D. Тобто ми можемо простежити, як змінюється сума квадратів сторін у паралелограмі. Отже, вважаємо, що досить розглянути змінення суми.
,де С і D - діагоналі , a і b - сторони. Ми бачимо, що змінюються сторони при зміненні діагоналі D. Тобто ми можемо простежити, як змінюється сума квадратів сторін у паралелограмі. Отже, вважаємо, що досить розглянути змінення суми.
Побудуємо ромб, задамо діапазон діагоналі D, і будемо мати на увазі, що сторони нашого ромба A і B нетотожні сторонам трикутника a і b. Але сума сторін однакова : ![]() , так як основу С=c задано незмінною, а діагональ D має те ж саме значення, яке вона має і в первісному паралелограмі (рис. 2.4).
, так як основу С=c задано незмінною, а діагональ D має те ж саме значення, яке вона має і в первісному паралелограмі (рис. 2.4).
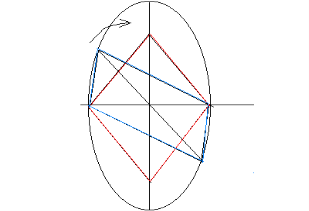 Рис.2.4
Рис.2.4
На рисунку 2.5 зліва зображено трикутники, які відповідають формулі 2.1, але з різними сторонами a і b. З правого боку рисунка 2.5 зображено перетворені трикутники, в яких дві сторони рівні, але С=c, і висота (вона ж медіана) трикутника, зображеного праворуч, дорівнює медіані трикутника, зображеного ліворуч.


![]()
![]()
![]()
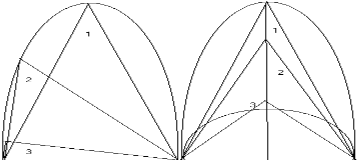 Рис.2.5
Рис.2.5
Для паралелограма й ромба справедлива формула![]() .
.
А значить, виконується тотожність:![]() (так як діагоналі обох фігур рівні). Тут A і B - сторони ромба, a і b - сторони трикутника, відповідного первісній формулі (2.1). Зрозуміло, що величина діагоналі D змінюється в межах від максимального значення (при a = b)до мінімального значення ( при D = C ). Сторони трикутника "1", на рисунку 2.5 підпорядковані залежності:
(так як діагоналі обох фігур рівні). Тут A і B - сторони ромба, a і b - сторони трикутника, відповідного первісній формулі (2.1). Зрозуміло, що величина діагоналі D змінюється в межах від максимального значення (при a = b)до мінімального значення ( при D = C ). Сторони трикутника "1", на рисунку 2.5 підпорядковані залежності:![]() де с - основа, а і b - сторони.
де с - основа, а і b - сторони.
У разі рівних діагоналей, що відповідає трикутнику "3" на рисунку 2.5, трикутник є прямокутним, де С - його гіпотенуза, а значить виконується тотожність: ![]() ( Теорема Піфагора)
( Теорема Піфагора)
Якщо С задано сталою, і сторони трикутника рівні, то нехай висота трикутника залежить від степеня, в який зведено цей вираз. Тоді трикутнику "2", відповідає вираз:![]() ; трикутнику "1":
; трикутнику "1":![]() ; і т.д. Отже, трикутник виду
; і т.д. Отже, трикутник виду![]() перетворюється в трикутник виду
перетворюється в трикутник виду ![]()
![]() Нехай, деякий трикутник виду
Нехай, деякий трикутник виду![]() , при цьому m <n, буде рівнобедренним. Для перетвореного трикутника, в якому сторони рівні:
, при цьому m <n, буде рівнобедренним. Для перетвореного трикутника, в якому сторони рівні:
![]() ;
;
 Рис 2.6
Рис 2.6
З рис. 2.6 ![]() ,
, ![]() +
+![]() ;
;
![]() =
=![]() +
+![]() =
=![]() –
–![]() =
= ![]()
Дане відношення стає раціональним тільки при степені m = 2.
Висновок : Рішення рівняння ![]() в цілих числах існують при показнику степеня n
в цілих числах існують при показнику степеня n![]() , а при степенях n
, а при степенях n![]()
![]() цілих рішень немає.
цілих рішень немає.
РОЗДІЛ 3
ТЕОРЕМА ФЕРМА В ЛІТЕРАТУРІ ТА МИСТЕЦТВІ
Велика теорема Ферма стала символом запеклої наукової проблеми і в цій якості часто згадується в белетристиці. Далі наведені деякі твори, в яких теорема є суттєвою частиною сюжету чи є красномовним епізодом. Поштова марка Чехії 2000 року, яку видано до Всесвітнього року математики, символізує перемогу над непідступністю Великої теореми Ферма.
3.1. Сюжетна лінія про теорему Ферма в літературних творах
У романі Стіга Ларссона «Дівчина, яка грала з вогнем» головна героїня Лісбет Саландер, яка володіє рідкісними здібностями до аналітики і фотографічною пам'яттю, має хобі. Вона зайнята Великою теоремою Ферма. Весь свій вільний час вона присвячує самостійному пошуку «видатного доведення» теореми великого француза, але раз по раз заходить в глухий кут. В кінці книги Лісбет знаходить підтвердження, яке не тільки абсолютно відмінно від запропонованого, але і є настільки простим, що сам Ферма міг би його знайти. Однак, Ларссон не приводить цього доказу.
У повісті Е. Велтистова «Переможець неможливого» другСироїжкіна і Електроніка, Вова Корольков, в якості вільного завдання з математики довів Велику теорему Ферма.
В оповіданні Артура Порджес «Саймон Флегг і диявол» професор Саймон Флегг просить допомоги диявола в доведенні теореми, але і диявол виявляється безсилий.
В оповіданні Кіра Буличова «Мрія заочника» студент-заочник Гаврилов приходить до професора Мінца і приносить куплену курсову роботу, в якій наводиться доказ теореми, з проханням пояснити, що він написав.
У першому виданні «Мистецтва програмування» Дональда Кнута теорема Ферма наведена в якості вправи з математичним ухилом на самому початку книги і оцінена максимальним числом 50баллов, як «дослідницька проблема, яка ще не отримала задовільного рішення».
В оповіданні Наталії Дар’ялової «Велика і загадкова» сюжет будується на теоремі Ферма. Розповідається про те, як молодий студент зайнявся теоремою Ферма. Згодом він став математиком, отримав кілька важливих наукових результатів, але абсолютно занапастив своє особисте життя.
У романі Павла Загребельного «Розгін» скромний викладач математики з Одеси зумів довести теорему. Через деякий час він стає академіком і очолює дуже серйозне Київське НПО, яке займається створенням електронно-обчислювальних систем.![]()
- Згадки про теорему Ферма в кіномистецтві, мистецтві
У 1979 році знятий на Одеській кіностудії дитячий музичний трисерійний телефільм «Пригоди Електроніка» режиссера К. Бромберга. Сюжет фільму за мотивами фантастичних повістей Є.Велтистова «Електронік - хлопчик з чемодана» і «Рессі - невловимий друг».
За оповіданням Артура Порджес «Саймон Флегг і диявол» був також знятий ігровий науково-популярний фільм «Математик і чорт».
У телесеріалі «Зоряний Шлях», капітан космічного корабля Ентерпрайз NCC-1 701-D Жан-Люк Пікар був спантеличений розгадкою Великої теореми Ферма в другій половині XXIV століття. Творці фільму припускали, що рішення у Великої теореми Ферма не буде найближчим часом. Серія «Рояль» з цим епізодом була знята в 1989 році, коли Джон Уайлс був на самому початку своїх робіт. Насправді ж рішення було знайдено всього через 5 років.
Мюзикл «Останнє танго Ферма», виданий інститутом Клея, створений в 2000 році Дж. Розенблума і Дж. С. Лессер за мотивами реальної історії Ендрю Уайлса. Головний герой на ім'я Деніел Кін завершує доведення теореми, а дух самого Ферма намагається йому перешкодити.
ЗАКЛЮЧЕННЯ
Ферма висловив таке твердження: « Якщо число a не ділиться на просте число p, то існує такий показник k, що a-1 ділиться на p, причому k є дільником p-1» Це твердження увійшло в історію як Мала теореми Ферма. Воно є основним у всій елементарній теорії чисел. ![]()
Застосовуючи дане твердження, я все ж спробувала довести справедливість теореми Ферма.
Поставимо собі задачу:
Дослідження справедливості теореми Ферма при n = 3. Переконаємось, що рівняння ![]() для простого
для простого ![]() нерозв'язне в натуральних числах.
нерозв'язне в натуральних числах.
Доведення
Доведемо це твердження методом від противного. Припустимо, що задане рівняння має рішення в натуральних числах x0, y0, z0, де z0 - просте число. Тоді вірна числова тотожність![]() =
= ![]()
Розкладемо ліву частину цього виразу на множники:
![]() =
=![]() (1)
(1)
Так як добуток, сума і різниця натуральних чисел є число натуральне, то ліва частина числової тотожності (1) представлена у вигляді добутку двох натуральних чисел, а значить і права частина цієї тотожності може бути представлена у вигляді добутку двох натуральних чисел. Так як ![]() - просте число, то
- просте число, то ![]() може бути представлено у вигляді добутку двох натуральних чисел тільки наступними чотирма способами:
може бути представлено у вигляді добутку двох натуральних чисел тільки наступними чотирма способами:
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
Значить, ![]() і
і ![]() повинні бути рішеннями хоча б однієї з таких систем рівнянь:
повинні бути рішеннями хоча б однієї з таких систем рівнянь:
![]() (2.1)
(2.1)
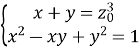 (3.1)
(3.1)
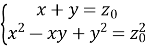 (4.1)
(4.1)
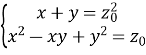 (5.1)
(5.1)
Покажемо, що жодна з цих систем не має рішення в натуральних числах.
Попередньо зауважимо, що ![]() не існує розв’язків в натуральних числах при
не існує розв’язків в натуральних числах при ![]() рівних 1 або 2 :
рівних 1 або 2 :![]() ;
;
![]() ;
;![]()
Тому, зазначені вище значення ![]() слід виключити з розгляду.
слід виключити з розгляду.
Зі способу (2) стає зрозумілим , що система (2.1) не має розв’язків, так як не існує таких натуральных ![]() , сумма яких дорівнювалась би 1.
, сумма яких дорівнювалась би 1.
Розглянемо спосіб (3): 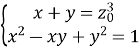 ;
;![]()
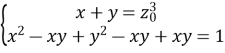 ;
;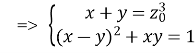 ;
;
Так як ![]() 2 и
2 и ![]() , то
, то ![]() .
.
Значить, система (3.1) рішень не має.
Зі способу (4): 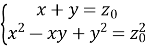 ;
;![]()
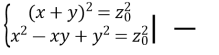 ;
;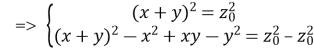 ;
;![]()
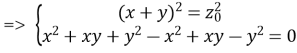 ;
;![]()
![]()
Але, за умовою задачі x≠0 і y≠0. Значить, система (4.1) не має рішень.
Зі способу (5) при ![]() очевидно , що
очевидно , що ![]()
Отже, повинна виконуватися нерівність:
![]() (6)
(6)
Покажемо, що ця нерівність не виконується при x > 2 и y > 2.
Припустимо, що![]() , тоді
, тоді ![]()
![]() ;
;
При будь-яких![]()
Покажемо, що![]() для x
для x![]() 2 і y
2 і y![]() 2
2 ![]()
![]()
При x = 2 і y = 2 маємо 1=![]()
При x > 2 і y > 2 , тобто![]() і
і![]() , маємо
, маємо ![]()
![]()
Отже, нерівність (6) невірна. Значить, система (5.1) не має рішень.
Висновок:
Таким чином, доведено, що рівняння ![]() , де z - просте число, неможливо розв'язати в натуральних числах.
, де z - просте число, неможливо розв'язати в натуральних числах.
Слід зауважити, що метод, застосований для доведення неможливості розв'язання в натуральних числах рівняння ![]() для простого z може бути застосований і в завданні з розширеним формулюванням:
для простого z може бути застосований і в завданні з розширеним формулюванням:
Рівняння ![]() нерозв'язне в натуральних числах, якщо одна зі
нерозв'язне в натуральних числах, якщо одна зі
змінних (x, y або z) є простим числом. Так, якщо не z, а y - просте число,
то рівняння представимо у вигляді: ![]()
Розкладемо на множники: ![]()
Подальше доведення проводиться за аналогією з попереднім.
Таким чином, рівняння ![]() , де x, y або z - просте число, нерозв'язне в натуральних числах.
, де x, y або z - просте число, нерозв'язне в натуральних числах.
ВИСНОВОК
Рівняння ![]() має цілі рішення лише у випадку, коли набуває виду
має цілі рішення лише у випадку, коли набуває виду ![]() . У шкільному курсі математики є приклади застосування цього великого відкриття.
. У шкільному курсі математики є приклади застосування цього великого відкриття.
Приклад 1.
При n = 2 ми застосовуємо дане твердження під назвою «Теорема Піфагора» ![]() , де x,y – катети, z – гіпотенуза прямокутного трикутника. Ми можемо побудувати безліч прямокутних трикутників з цілочисленими сторонами, кратними до «трійки» чисел 3, 4, 5.
, де x,y – катети, z – гіпотенуза прямокутного трикутника. Ми можемо побудувати безліч прямокутних трикутників з цілочисленими сторонами, кратними до «трійки» чисел 3, 4, 5.
Приклад 2.
При n = 2 існують Піфагорові трійки взаємно простих чисел : 3,4,5; 5,12,13; 7,24,25; 8,15,17; 9,40,41 та інші. ![]()
Приклад 3.
При n = 2 ми застосовуємо дане твердження як рівняння кола на площині:
![]()
![]() , де (х; у) – координати точок кола, z - радіус кола, (0;0) – центр кола. Слід зазначити, що поряд з будь-якими координатами точок кола можна знайти цілочислені координати ( х;у) кола.
, де (х; у) – координати точок кола, z - радіус кола, (0;0) – центр кола. Слід зазначити, що поряд з будь-якими координатами точок кола можна знайти цілочислені координати ( х;у) кола.



![]() Y
Y
![]() Охх
Охх
X
Рис 3.
Підводячи підсумок, можна з упевненістю сказати, що математика вчить правильно і послідовно мислити, логічно міркувати. У формуванні багатьох якостей, необхідних успішній сучасній людині, велику роль відіграє математика. На уроках математики ми вчимося розмірковувати, доводити, знаходити раціональні шляхи виконання завдань, робити відповідні висновки. Загальновизнано, що «математика - найкоротший шлях до самостійного мислення».![]() На часі інтеграція знань, на часі освічена людина, «яка, здатна до самоосвіти і саморозвитку, - вміє критично мислити, опрацьовувати різноманітну інформацію, …прагне змінити на краще своє життя та життя своєї країни»
На часі інтеграція знань, на часі освічена людина, «яка, здатна до самоосвіти і саморозвитку, - вміє критично мислити, опрацьовувати різноманітну інформацію, …прагне змінити на краще своє життя та життя своєї країни» ![]() . Наразі, математика і література не такі вже й далекі один від одного. Мистецтво і наука вимагають фантазії, творчої сміливості і спостереження різних явищ життя. Популяризація математичної культури через непідступну теорему Ферма в художніх творах суттєвий тому приклад. Отже, цитуючи К.Д. Ушинського, «знання та ідеї, що повідомляються якими б то не було науками, повинні органічно будуватися в світлий і, по можливості, широкий погляд на світ і його життя»
. Наразі, математика і література не такі вже й далекі один від одного. Мистецтво і наука вимагають фантазії, творчої сміливості і спостереження різних явищ життя. Популяризація математичної культури через непідступну теорему Ферма в художніх творах суттєвий тому приклад. Отже, цитуючи К.Д. Ушинського, «знання та ідеї, що повідомляються якими б то не було науками, повинні органічно будуватися в світлий і, по можливості, широкий погляд на світ і його життя»![]() . Тільки в тісному взаємозв'язку різних наук людина відчуватиме себе спокійно, впевнено, комфортно в цьому величезному світі див та таємниць.
. Тільки в тісному взаємозв'язку різних наук людина відчуватиме себе спокійно, впевнено, комфортно в цьому величезному світі див та таємниць.
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ
1. Постніков М.М. Введение в теорию алгебраических чисел. ![]() / Москва, М.: Наука, 1982. - с.130
/ Москва, М.: Наука, 1982. - с.130
2. Болгарський Б. В. Нариси з історії математики / Мінськ, М: Знання, 1979. – с.37-42
3. Вигодський М. Я. Довідник з елементарної математики / Москва, М: Наука, 1974. – с.92
4. Вигодський М. Я. «Збірник завдань з елементарної математики»; Москва, Наука , 1963. – с. 102
5. Ферма теорема // Математическая энциклопедия/. – М. : Советская Энциклопедия, 1985. — Т. 5., с. 307
6. Щербина В.А., Довгаль М.М. Інтеграція предметів як перспективний напрямок модернізації середньої освіти на сучасному етапі // Особистість, сім'я і суспільство: питання педагогіки і психології: зб. ст. по матер. XX міжнар. наук.-практ. конф. - Новосибірськ: СібАК, 2012
7. Колегія МОН України // Постанова № 12/5-2 від 22.11.2001 ![]() / м. Київ, 2001.
/ м. Київ, 2001.
8. ІНТЕРНЕТ РЕСУРСИ
8.1. Велика теорема Ферма [Вікіпедія ]: https://uk.wikipedia.org/wiki
8.2. Математика та література ; http://www.psyh.kiev.ua.;
8.3. Візуалізація теореми Ферма ; https://www.youtube.com/watch?v=KjEoh2KUZyU


про публікацію авторської розробки
Додати розробку
