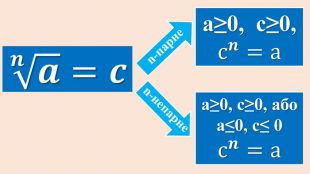
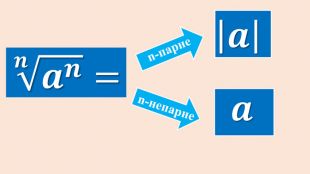
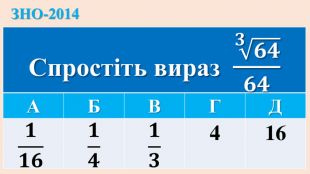
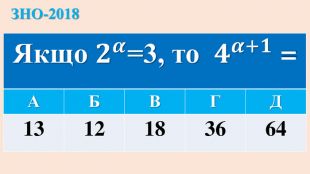
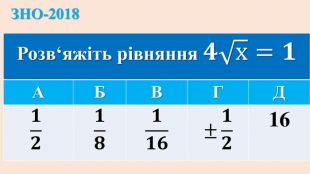
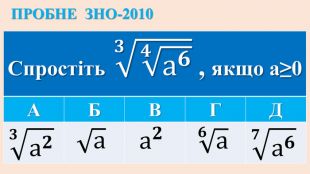
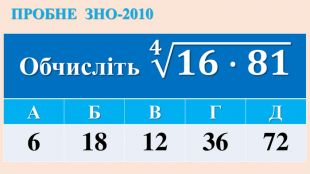
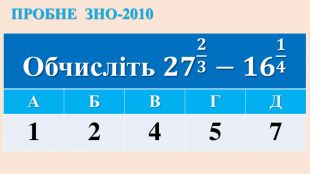
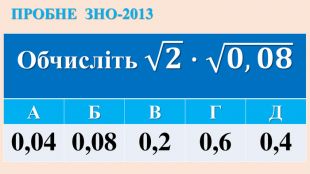
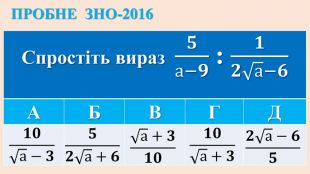
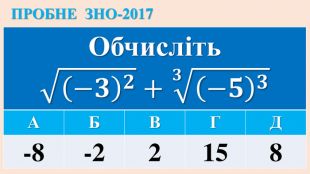
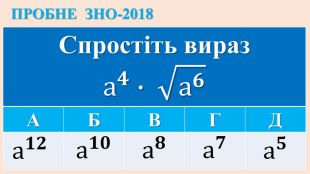
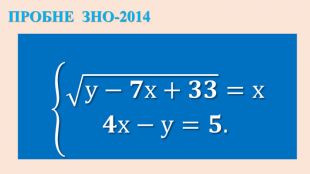Опорні схеми з теми "Корінь n-го степеня. Степінь з раціональним показником". Умови завдань ЗНО з даної теми.
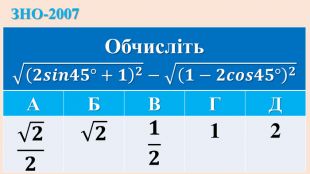
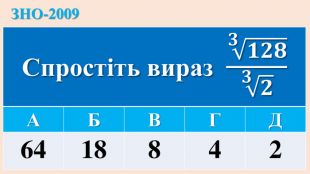
Дані опорні схеми є своєрідною "шпаргалкою" для учнів. Систематизовано і узагальнено навчальний матеріал з теми "Корїнь n-го степеня. Степінь з раціональним показником". Подані алгоритми розв"язання основних типів ірраціональних рівнянь і нерівностей. Наведено розв"язки характерних завдань з даної теми, які пропонувались випускникам старшої школи під час ЗНО.












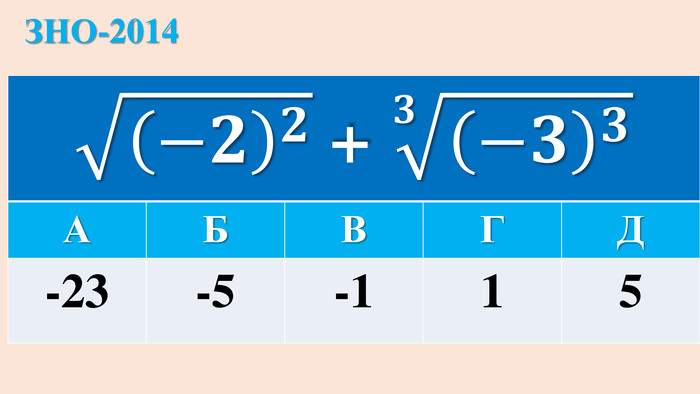
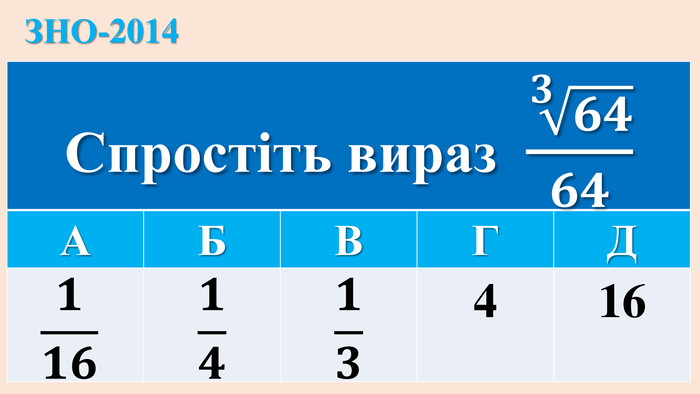




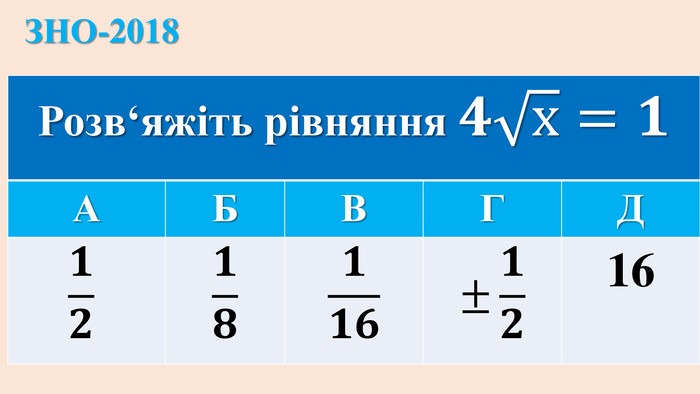

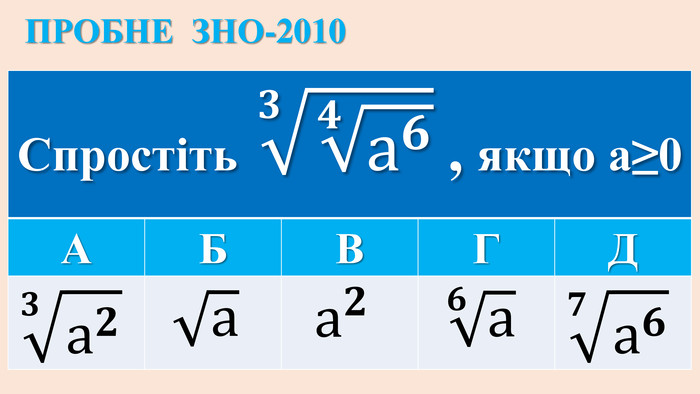
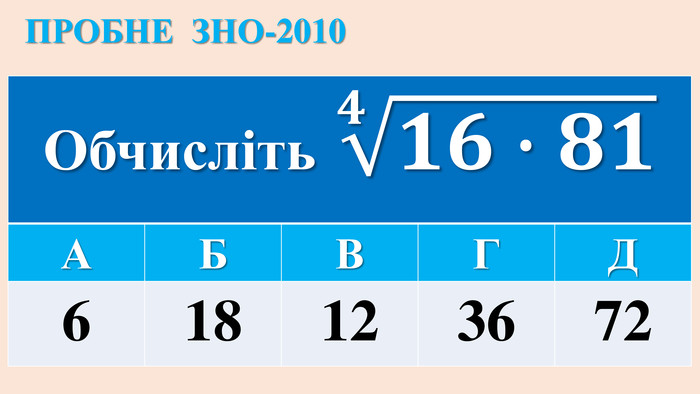
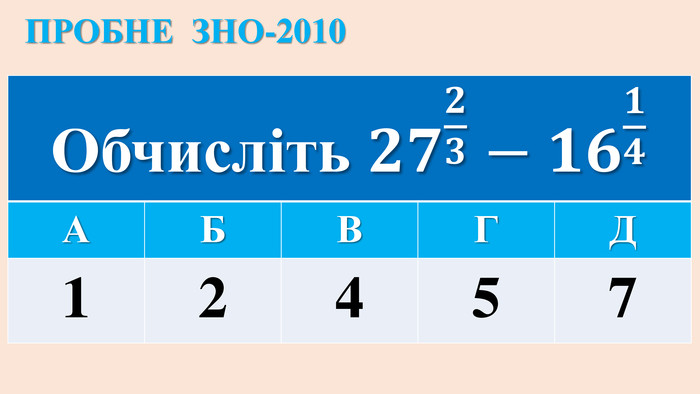

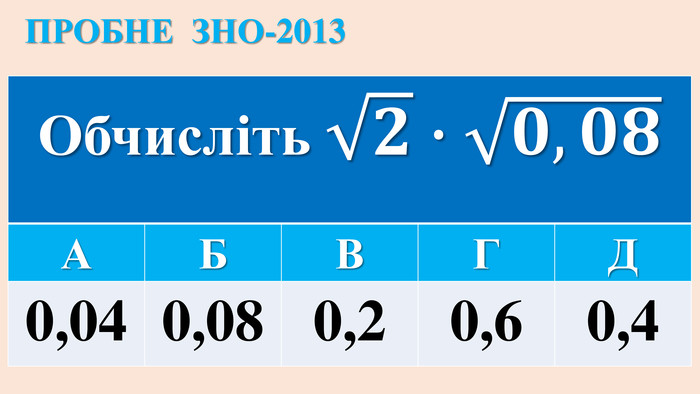

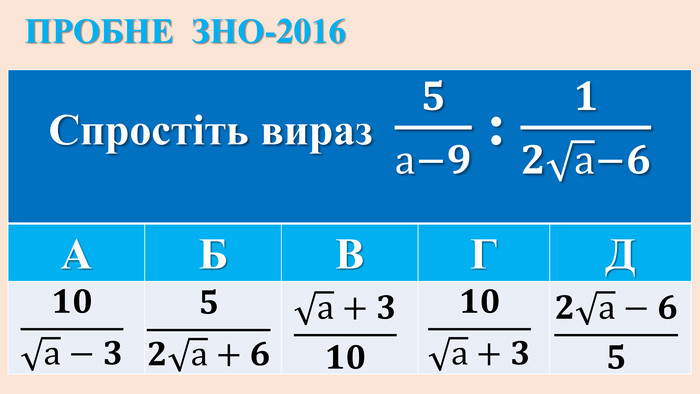

















ІРРАЦІОНАЛЬНІ РІВНЯННЯ{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}ТИП РІВНЯННЯСПОСІБ РОЗВ‘ЯЗАННЯ1.𝒏𝒇(𝒙)=𝒄, с-числоf(x)=𝒄𝒏 (с≥0); немає коренів (с<0 і n –парне)2.𝒏𝒇(𝒙)=𝒏𝒈(𝒙)f(x) = g(x) Перевірка коренів, якщо n-парне!3.𝒇(𝒙) = ax+b𝒇𝒙= 𝒂𝒙+𝒃𝟐 Перевірка коренів!4.𝒄𝒇𝒙+𝒎 = af(x)+b. ЗАМІНА: f(x)= y→ р-ння 3 Перевірка коренів рівняння 𝒄𝒚+𝒎=𝒂𝒚+𝒃!5. 𝒎𝒙+𝒅 + 𝒏𝒙+𝒄=𝐚Піднесення двох частин до квадрату (2 рази)Перевірка коренів!6.c𝒏𝒇(𝒙)+𝒎𝟐𝒏𝒇(𝒙)=𝒅ЗАМІНА: 𝟐𝒏𝒇𝒙 = y → квадратне рівняння→ рівняння 1. {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}ТИП РІВНЯННЯСПОСІБ РОЗВ‘ЯЗАННЯf(x) = g(x) Перевірка коренів, якщо n-парне!Піднесення двох частин до квадрату (2 рази)Перевірка коренів!
ІРРАЦІОНАЛЬНІ НЕРІВНОСТІ{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}ТИП НЕРІВНОСТІСПОСІБ РОЗВ‘ЯЗАННЯ𝒏𝒇(𝒙)>𝒄, с-число𝒇(𝒙)>𝒄𝒏 (с≥0 або n –непарне ); 𝒇(𝒙)≥𝟎 (с<0 і n –парне)𝒏𝒇(𝒙)<𝒄, с-число𝒇(𝒙)<𝒄𝒏 (n –непарне ); 0≤𝒇(𝒙)<𝒄𝒏 (с≥0 і n –парне)не має розв‘язків (с<0 і n –парне)𝒏𝒇(𝒙)>𝒏𝒈(𝒙)f(x) > g(x), n –непарне; 𝒇𝒙>𝒈𝒙,𝒈(𝒙)≥𝟎 , n –парне 𝒇(𝒙) >𝒈(𝒙) 𝒇𝒙>𝒈𝟐𝒙,𝒈(𝒙)≥𝟎 або 𝒇𝒙≥𝟎,𝒈(𝒙)<𝟎𝒇(𝒙) <𝒈(𝒙) 𝒇𝒙<𝒈𝟐𝒙,𝒈𝒙≥𝟎,𝒇(𝒙)≥𝟎{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}ТИП НЕРІВНОСТІСПОСІБ РОЗВ‘ЯЗАННЯ
ЗНО-2016{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Установіть відповідність між числовим виразом (1-4) та його значенням (А-Д)1𝟐𝟑𝟐 А42𝟏𝟒−𝟐 Б83𝟏𝟔𝟏𝟐 В164 𝟐𝟑,𝟓∙𝟐𝟏,𝟓 Г32 Д64{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Установіть відповідність між числовим виразом (1-4) та його значенням (А-Д)1 А42 Б83 В164 Г32 Д64
ЗНО-2017{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Нехай m, n –дійсні числа, а – додатнє число (а≠1). До кожного початку речення (1-4) доберіть його закінчення (А-Д)ПОЧАТОК РЕЧЕННЯЗАКІНЧЕННЯ РЕЧЕННЯ1 Якщо 𝒂𝒎𝒏= 𝒂𝟒, то. Аm + n = 42 Якщо 𝒂𝒏∙𝒂𝒎= 𝒂𝟒, то. Бm - n = 43 Якщо 𝟖𝒂𝒎 = 𝒂𝒏, то. Вmn = 44 Якщо 𝒂𝒏𝒂𝒎 = 𝟏𝒂𝟒, то. Гm = 8n. Дm = 4n {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Нехай m, n –дійсні числа, а – додатнє число (а≠1). До кожного початку речення (1-4) доберіть його закінчення (А-Д)ПОЧАТОК РЕЧЕННЯЗАКІНЧЕННЯ РЕЧЕННЯ1 Аm + n = 42 Бm - n = 43 Вmn = 44 Гm = 8n. Дm = 4n
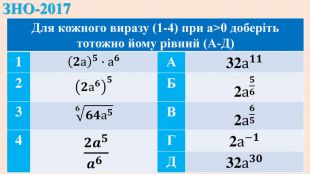
ЗНО-2017{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Для кожного виразу (1-4) при а>0 доберіть тотожно йому рівний (А-Д)1𝟐а𝟓∙а𝟔 А32а𝟏𝟏2𝟐а𝟔𝟓 Б2а𝟓𝟔3𝟔𝟔𝟒а𝟓 В2а𝟔𝟓4 𝟐𝒂𝟓𝒂𝟔 Г2а−𝟏 Д32а𝟑𝟎{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Для кожного виразу (1-4) при а>0 доберіть тотожно йому рівний (А-Д)1 А2 Б3 В4 ГД
ПРОБНЕ ЗНО-2011{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Установіть відповідність між числовим виразом (1-4) та його значенням (А-Д)1𝟑+𝟐𝟐-2𝟔 А152(𝟓−𝟐)(𝟓+𝟐)Б63𝟑𝟑−𝟏𝟐𝟐 В54 𝟐(𝟓𝟎−𝟖)Г3 Д1{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Установіть відповідність між числовим виразом (1-4) та його значенням (А-Д)1 А152 Б63 В54 Г3 Д1
-
 Новікова Анна Олександрівна 14.04.2019 в 16:20Загальна:5.0Структурованість5.0Оригінальність викладу5.0Відповідність темі5.0
Новікова Анна Олександрівна 14.04.2019 в 16:20Загальна:5.0Структурованість5.0Оригінальність викладу5.0Відповідність темі5.0

про публікацію авторської розробки
Додати розробку