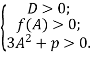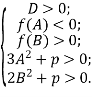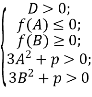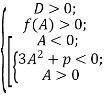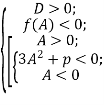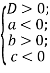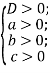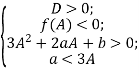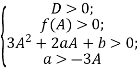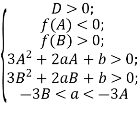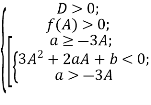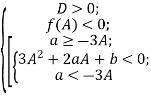Науково-дослідницька робота "ЗАСТОСУВАННЯ ВЛАСТИВОСТЕЙ КОРЕНІВ КУБІЧНОГО РІВНЯННЯ ДО РОЗВ′ЯЗУВАННЯ ЗАДАЧ ІЗ ПАРАМЕТРАМИ"

Міністерство освіти і науки України

Департамент освіти і науки

Львівської облдержадміністрації

СОКАЛЬСЬКА МАЛА АКАДЕМІЯ НАУК УЧНІВСЬКОЇ МОЛОДІ

 

 

Відділення: математика

Секція: математика

 

 

 

 

ЗАСТОСУВАННЯ ВлАСТИВОСТЕЙ КОРЕНІВ КУБІЧНОГО РІВНЯННЯ ДО РОЗВ′ЯЗУВАННЯ ЗАДАЧ ІЗ ПАРАМЕТРАМИ

 

 

 

Роботу  виконала:

Гнатюк Дарина Ігорівна,

учениця 10 класу Сокальського ліцею №1 імені Олега Романіва

Слухачка Сокальської МАН

 

Науковий керівник:

Кровіцька Лариса Ярославівна,

вчитель математики Сокальської МАН

 

 

 

 

 

Сокаль - 2019

ЗМІСТ

ВСТУП……………………………………………………………….

РОЗДІЛ І. КУБІЧНІ РІВНЯННЯ З ПАРАМЕТРАМИ В МАТЕМАТИЦІ

 

1.          Основні означення, які використовуються при розв'язувані рівнянь з параметрами
2.        Задачі, розв'язок яких застосовується для кубічних рівнянь
3.        Залежність коренів кубічного рівняння від дискримінанта D

 

РОЗДІЛ І. ДОСЛІДЖЕННЯ РОЗВ′ЯЗКІВ КУБІЧНОГО РІВНЯННЯ, В ЗАЛЕЖНОСТІ ВІД ПАРАМЕТРА

2.1.    Розміщення коренів рівняння відносно деякого числа А

2.2.    Застосування досліджуваних теорем для зведеного кубічного рівняння

 

РОЗДІЛ ІІІ. ЗАСТОСУВАННЯ ВЛАСТИВОСТЕЙ КУБІЧНОГО РІВНЯННЯ ДО РОЗВ'ЯЗУВАННЯ ЗАДАЧ, ЯКІ ВИКОРИСТОВУЮТЬСЯ НА ЗНО, МАТЕМАТИЧНИХ ОЛІМПІАДАХ ТА ТУРНІРАХ

 

ВИСНОВКИ………………………………………………………..

 

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ……………….

 

 

 

 

 

 

 

 

 

 

 

 

 

ВСТУП

 

      Вивчення багатьох фізичних процесів і геометричних закономірностей часто призводить до розв’язування завдань з параметрами. Завдання ЗНО також містять рівняння, нерівності та їх системи з параметрами, які часто є дуже складними і вимагають нестандартного підходу до розв’язання. У школі цей один з найбільш складних розділів шкільного курсу математики розглядається тільки в профільних класах, класах з поглибленим вивченням математики або на факультативних заняттях.

          Важливим є виявлення найбільш раціонального способу розв’язання, яке швидко приводить до відповіді. На мій погляд, графічний метод є зручним і швидким способом розв’язання значної кількості рівнянь і нерівностей з параметрами.

      Розв′язування багатьох абстрактних і прикладних задач зводиться до

розв′язування різних видів рівнянь.

   Метою моєї роботи є дослідити кубічні рівняння, і застосування властивостей їх коренів до розв′язування задач з параметрами, дослідити способи розв′язування кубічних рівнянь.

Актуальність дослідження полягає в тому, що розв’язки кубічних рівнянь і застосування властивостей коренів до розв’язування задач з параметрами досліджували вчені різних часів  і у школі це один з найбільш складних розділів шкільного курсу математики розглядається тільки в профільних класах, класах з поглибленим вивченням математики або на факультативних заняттях.

   Окремі види кубічних рівнянь розв′язували вчені Стародавньої Греції та давнього Китаю. Повну класифікацію кубічних рівнянь, а також загальний спосіб їх розв′язування за допомогою перетину кривих другого порядку дав видатний перський поет і вчений Омар Хайям. Він вигадав дуже важкі, але красиві способи геометричних побудов для

розв′язування кубічних рівнянь, а точніше, для доведення принципової можливості їх розв′язувати. З того часу вчені майже чотириста років  шукали формули для розв′язування кубічних рівнянь. Історія відкриття цих формул нагадує пригодницький роман. Але ні трагічна доля одних, ні невдачі інших не змогли зупинити дослідження, і в XVI ст. було відкрито спосіб розв′язування кубічних рівнянь. Формули, за якими можна розв′язувати кубічні кубічні рівняння, називають формулами Д. Кардано, хоча насправді їх автором був 

 Н. Тарталья.

     Багато сучасних збірників задач різного призначення містять кубічні рівняння з параметрами. Причому інколи потрібно не розв′язати рівняння, тобто знайти його корені,  а вказати кількість коренів при певних значеннях параметра, або вказати за яких значень параметра корені рівняння задовольняють певні умови. Ми звикли розв′язувати такі задачі для квадратних рівнянь: за знаком дискримінанта знаходимо кількість коренів, а за місцем коренів квадратного тричлена на числовій прямій досліджуємо їх розміщення щодо деяких заданих величин. Аналогічні задачі можна розв′язувати і для кубічних рівнянь.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

РОЗДІЛ 1. КУБІЧНІ РІВНЯННЯ З ПАРАМЕТРАМИ В МАТЕМАТИЦІ

 

1.1. Основні означення, які використовуються при розв'язувані рівнянь з параметрами

     Вивчення багатьох фізичних, геометричних та економічних закономірностей нерідко приводить до розв’язування завдань із параметрами. Найбільш складною і важливою частиною розв’язування таких завдань є дослідження процесу залежно від параметрів.

 Розв’язування завдань завдань з параметрами сприяє розвитку творчих компетенцій учнів.

 При цьому потрібно вміти застосовувати знання, уміння та навички, набуті раніше, індивідуально підходити до розв’язання кожного завдання.

  Розглянемо рівняння

          ,                           (1)

де a,b,c,....,k,x — змінні величини.

 Будь-яку систему значень змінних , , ,.. ., , , при якій і ліва і права частини цього рівняння набувають дійсних значень, називають системою допустимих значень змінних a,b,c, ...,k,x. Нехай A — множина всіх допустимих значень a, B — множина всіх допустимих значень b тощо , X — множина всіх допустимих значень x, тобто   Якщо кожної з множин A, B, C, ... ,K вибрати і зафіксувати по одному значенню a,b,c, ..., k і підставити їх у рівняння (1), то дістанемо рівняння відносно x, тобто рівняння з одним невідомим.

 Змінні f, b, c, ..., k які під час розв’язування рівняння вважають сталими, називають параметрами, а саме рівняння називають рівнянням, що містить параметри.

 Параметри позначають першими літерами латинського алфавіту: a, b, c, d, ..., k, l, m, n, а невідомі буквами x, y, z.

 Розв’язати рівняння з параметрами означає вказати, при яких значеннях параметрів існують розв’язки і які вони.

 Два рівняння, що містять одні й ті самі параметри, називають рівносильними, якщо:

1) вони мають зміст при одних і тих самих значеннях параметрів;

2) кожен розв’язок першого рівняння є розв′язком другого, і навпаки.

 

   Алгоритм розв’язання завдань графічним методом у системі xOy

1. Знаходимо область допустимих значень рівняння.

2. Запишемо рівняння у вигляді .
3. У системі координат xOy будуємо графіки функцій та для тих значень x, які належать області допустимих значень поданого рівняння.

4. Встановлюємо взаємне розташування графіків поданих функцій залежно від значень параметра a.

5. Якщо графіки перетинаються, то визначаємо абсциси точок перетину. Для цього достатньо розв’язати рівняння  відносно x.

6. Записуємо відповідь.

Рівнянням з параметрами називають рівняння виду:

                      

де x — шукане невідоме,  - змінні параметри. Значення шуканого невідомого  x залежить від значень параметрів.

 Найчастіше зустрічаються такі задачі з параметрами:

- для кожного значення параметра знайти всі розв’язки поданого рівняння або нерівності;

- знайти всі значення параметра, при кожному з яких розв’язки рівняння або нерівності задовільняють подані умови.

 Допустимими значеннями параметрів називають такі їх значення, при яких вираз

                        

має зміст при деяких значеннях  x.

 Областю зміни параметрів називають множину всіх допустимих систем значень параметрів рівняння.

 Для кожної допустимої системи значень параметрів рівняння має певну множину розв’язків.

 Розв’язати рівняння з параметрами означає знайти всі розв’язки цього рівняння для кожної допустимої системи значень параметрів.

 Щоб розв’язати рівняння

                     

з невідомим  x і параметрами потрібно:

- знайти область допустимих значень параметрів ;

- розв’язати рівняння відносно  x і подати невідоме  x у вигляді функції

                    ;

- з’ясувати, при яких допустимих системах значень параметрів значення функції

                    є розв’язками даного рівняння;

- розглянути рівняння

                     

 при таких допустимих системах значень параметрів, при яких його не можна розв’язати    

 відносно  x;

- з’ясувати, чи має рівняння при цих значеннях параметрів розв’язки, і якщо має, то які.

 Необхідною складовою розв’язування завдань із параметрами є дослідження.

 

1.2.   Задачі, розв'язок яких застосовується для кубічних рівнянь

 

    Нехай дано кубічне рівняння у загальному вигляді:

    Якщо , то поділимо обидві частини рівняння на , отримає рівняння:

.                                                             (1)

    Підстановка приведе вказане рівняння до вигляду:

;

.

      Позначимо: ,  .

      Отримаємо неповне кубічне рівняння:

.                                                                      (2)

      Як бачимо, підстановкою будь-яке кубічне рівняння можна звести до рівняння вигляду (2). А тоді, знаючи y, можна знайти значення x.

   Отже, щоб розв′язати рівняння (1), досить вміти розв′язувати рівняння вигляду (2). А для такого рівняння існує формула, за якою знаходяться його корені. Це формула Кардано, яка має вигляд:

.

       Застосовуючи цю формулу, потрібно для кожного значення

   брати те значення

, для якого виконується умова .

       Користуючись цією формулою, можна розв′язати будь-яке кубічне рівняння.

 Позначимо вираз ,  тоді вираз називається дискримінантом кубічного рівняння.

   Ми знаємо, що кількість коренів квадратного рівняння залежить від знака дискримінанта. При квадратне рівняння має має два дійсних корені, при   -  один (два корені, що збігаються), при - дійсних коренів немає.

     Подібна залежність існує і для кубічного рівняння.

 

1.3.    Залежність коренів кубічного рівняння від дискримінанта D

 Теорема 1. Нехай -  неповне кубічне рівняння з дійсними коефіцієнтами і   -  дискримінант цього рівняння. Дане рівняння має:

 1) три різні дійсні корені тоді і тільки тоді, коли ;

 2) три дійсні корені, два з яких збігаються (при ) або всі три збігаються (при ) тоді і тільки тоді, коли ;

 3) один дійсний корінь і два комплексно спряжені тоді і тільки тоді, коли [3].

 Наведена теорема дає можливість досліджувати кількість коренів неповного кубічного рівняння, але цією теоремою можна користуватися і у випадку повного кубічного рівняння. Для цього досить виразити p і q через коефіцієнти даного рівняння за формулами , .

 З а у в а ж е н н я. Оскільки при рівняння (1) має один дійсний корінь, то у цьому випадку можна не знаходити дискримінант, а відразу робити висновки про кількість коренів рівняння. Умова рівнозначна умові для випадку повного кубічного рівняння. Тому при рівняння має один дійсний корінь.

 Задача 1. За яких значень параметра рівняння має один дійсний корінь?

 Розв′язання.

 1. За умовою задачі , тобто при . Отже, при рівняння має один дійсний корінь.

 2. Нехай . Рівняння матиме один дійсний корінь при ( ).

.

 

.

 Відповідь: .

 Задача 2. Залежно від значень параметра встановити кількість розв′язків рівняння .

 Розв’язання. Знайдемо і :

 ;

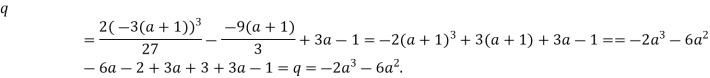
 Тоді

 

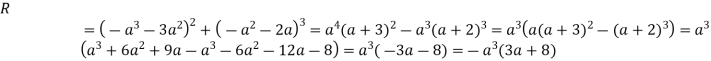
 Отже, . Маємо: 

  при - рівняння має три різні дійсні корені;

  при - рівняння має один дійсний корінь;

  при , при , тому при рівняння має два дійсні корені, а при рівняння має один дійсний корінь.

 Відповідь: якщо , то рівняння має три різні дійсні корені; якщо рівняння має два дійсні корені; якщо , то рівняння має один дійсний корінь.

 

 Задача 3. Залежно від значень параметра встановіть кількість розв′язків системи рівнянь

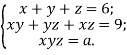
 Розв’язання. Вказана система — це запис теореми Вієта для кубічного рівняння. Тому розв′язки системи є коренями кубічного рівняння

 . Розв’язуючи симетричні системи, потрібно врахувати, що, отримавши один розв’язок, шляхом перестановки отримаємо інші. Тому якщо відповідне кубічне рівняння має три різні дійсні корені , то шляхом перестановки з розв′язку отримаємо шість розв′язків системи. Якщо рівняння має два дійсні корені, то система матиме три розв′язки. Якщо рівняння має один корінь кратності три, то система матиме один розв’язок. Якщо рівняння має один дійсний корінь кратності один, то система розв′язків не матиме.

 Дослідимо зазначене рівняння на кількість розв′язків.

      ;

      ;

      .

 Якщо , , , то рівняння має один дійсний корінь. Отже, система розв′язків не матиме.

 Якщо , , то рівняння матиме два дійсні корені. Отже, система матиме три розв′язки.

 Якщо , то рівняння має три різні дійсні корені. Тоді система матиме шість розв′язків.

 Відповідь: якщо - система розв′язків не має; якщо - система має 6 розв′язків; якщо - система має 3  розв′язки.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

РОЗДІЛ 2. ДОСЛІДЖЕННЯ РОЗВ'ЯЗКІВ КУБІЧНОГО РІВНЯННЯ, В ЗАЛЕЖНОСТІ ВІД  ПАРАМЕТРА

 

2.1.   Розміщення коренів рівняння відносно деякого числа А

 

   Розв’язуючи задачі з параметрами на дослідження коренів квадратного рівняння, часто користуються не дослідженням самих коренів, а їх розміщенням на числовій прямій. Це зручно робити у тому випадку, коли дискримінант квадратного рівняння не є повним квадратом.

 Розв’язуючи задачі, в яких потрібно дослідити корені кубічного рівняння, знаходять похідну функції, яка визначається цим рівнянням, її критичні точки та значення функції у цих точках. Потім досліджують ці значення. Цей метод дуже дієвий у випадку, коли дискримінант похідної є повним квадратом і критичні точки будуть "красиві". В іншому випадку краще досліджувати розміщення коренів кубічного рівняння.

 Встановимо властивості розміщення коренів спочатку для неповного кубічного рівняння.

 Нехай дано рівняння

.

 Раніше було встановлено, що при це рівняння (3) має єдиний дійсний корінь, причому при , при , при .

 Нехай . Надалі проводитимемо дослідження для випадку, коли рівняння (3) має три різні дійсні корені, тобто . Розглянемо функцію

 . , - критичні точки. Оскільки критичні точки — протилежні числа, то один із коренів рівняння менший за , а інший — більший за , тобто один із коренів від′ємний, а інший — додатний. Отже, всі три корені рівняння бути одночасно додатними або від′ємними не можуть. Якщо два корені від′ємні, то . Якщо два корені додатні, то .

 Розглянемо розміщення коренів відносно деякого числа А.

 Теорема 2. Всі три корені рівняння (3) більші за число тоді і тільки тоді, коли виконуються умови

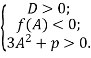
 Доведення.

 І. Нехай корені рівняння (3) більші за А, тобто .

 Доведемо, що тоді виконуються умови теореми. Оскільки всі три корені існують, то умова виконується.

 Нехай і - критичні точки функції , графік якої зображено на малюнку. Очевидно, що . Отже, і лежать правіше від А.

 

 Користуючись розміщенням коренів квадратного тричлена, це буде рівносильно виконанню умов

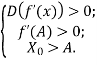
тобто має використовуватися умова . Оскільки , то

 . Отже, умова виконується.

 Доведемо виконання умови . Функція при зростає. Тоді при . Оскільки , то .

 Отже, якщо всі корені рівняння (3) більші за А, то умови теореми виконуються.

 ІІ. Нехай для рівняння (3) виконуються умови теореми. Доведемо, що всі корені рівняння більші за число А, тобто . Припустимо супротивне. Нехай . Оскільки при функція набуває лише додатних значень і , то , що неможливо, бо за умовою . Отримали протиріччя.

 Припустимо, що . Тоді . Оскільки при

спадає, то , , тоді , тобто

 , що неможливо, бо за умовою теореми .

 Припустимо, що . Це теж неможливо, оскільки .

 Отже, з усіх можливих варіантів розміщення точок відносно А, умову теореми задовольняє лише один, а саме .

 Теорему доведемо.

 Інші властивості розміщення коренів неповного кубічного рівняння наведені у таблиці 1.

Таблиця 1

1.	↔
2.	↔
3.	↔
4.	↔
5.	↔
6.	↔
7.	↔

 Для дослідження зведеного кубічного рівняння

                       (4)

 можливі два варіанти:

 Оскільки незалежно від виду рівняння потрібно знаходити дискримінант, тобто знаходити p і q, то можна скористатися умовами розміщення коренів неповного кубічного рівняння, але при цьому потрібно пам′ятати, що числа A і B зміняться. Тому потрібно розглядати розміщення коренів відносно нових чисел і  , які визначаються за формулами ,  , оскільки при переході від повного кубічного рівняння до неповного ми робили заміну

 .

 

2.2.   Застосування досліджуваних теорем для зведеного кубічного рівняння

 

 Встановимо теореми, подібні до попередніх, для зведеного кубічного рівняння виду (4).

 Теорема 3. Всі три корені рівняння (4) додатні тоді і тільки тоді, коли виконуються умови

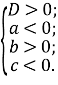
  Доведення.

1. Припустимо, що всі корені рівняння (4) додатні. Доведемо, що тоді виконуються теореми. Розглянемо функцію .

 Очевидно, якщо всі корені додатні, то мають виконуватися умови

 Оскільки , то перша умова рівносильна умові . Враховуючи розміщення коренів квадратного тричлена, умови , рівносильні умовам , , . Розглянемо ці умови.

 , a < 0.

 Умова   виконується завжди, бо ми припустили, що рівняння (4) має три корені, отже – існують, звідки   Отже, якщо всі корені рівняння (4) додатні, то

 2. Нехай для рівняння (4) виконуються умови  .  Доведемо, що всі корені рівняння додатні. Якщо , то за теоремою Вієта що можливо, якщо всі корені додатні, або два від′ємні і один додатний. Припустимо, що рівняння має два від′ємні корені. Тоді Оскільки

  то що суперечить умові   Отже, наше припущення неправильне, і всі три корені рівняння додатні.

 Теорему доведено.

 Аналогічно можна сформулювати та довести інші властивості розміщення коренів зведеного кубічного рівняння (див. таблицю 2).

Таблиця 2

1.		↔
2.		↔
3.		↔
4.		↔
5.		↔
6.		↔
7.		↔
8.		↔
9.		↔

 

 

 

 

 

 

РОЗДІЛ 3. ЗАСТОСУВАННЯ ВЛАСТИВОСТЕЙ КОРЕНІВ КУБІЧНОГО РІВНЯННЯ ДО РОЗВ'ЯЗУВАННЯ  ЗАДАЧ З ПАРАМЕТРАМИ, ЯКІ ВИКОРИСТОВУЮТЬСЯ НА ЗНО, МАТЕМАТИЧНИХ ОЛІМПІАДАХ ТА ТУРНІРАХ.

 

Задача 4. При якому значенні параметра а всі три корені рівняння

  більші за -2?

 Розв′язання. Розглянемо функцію: Корені рівняння будуть більші за -2, якщо виконуються умови

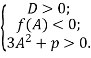
1)

2)

3)

 Отже, отримали систему

        

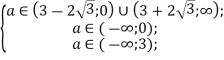
 Відповідь:

 Задача 5. За яких значень параметра а всі три корені рівняння

  належать проміжку ?

 Розв′язання. Розглянемо функцію

Для того щоб всі корені належали відрізку  , мають виконуватися умови

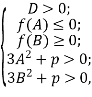      тобто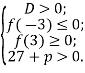

 1)

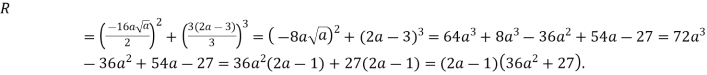
при тобто при .

 2)

 3)

.

 4)

 Тоді, повертаючись до системи, отримаємо

      

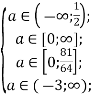
 Відповідь:

 Задача 6. За яких значень параметра а корені рівняння належать проміжку ?

 Розв′язання.

Перший спосіб. Запишемо умови, які мають виконуватися у даному випадку

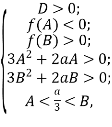
 де

1. 

2. 

3. 

4. 

5. 
6. 

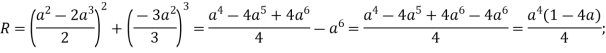
Повертаючись до системи, отримаємо

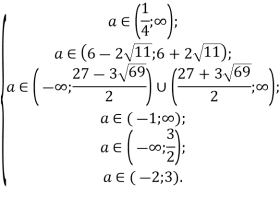
 Відповідь:

 Другий спосіб. Зробимо заміну яка зведе дане рівняння до неповного кубічного рівняння. Тоді проміжок перейде у проміжок , тобто нам треба дослідити рівняння на проміжку  .

Для цього мають виконуватися умови

 

За доведеним раніше при

 

 

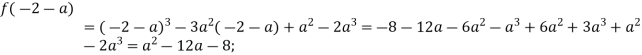
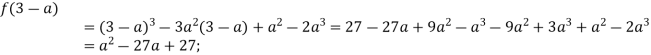
 Повертаючись до системи, отримаємо

 

 

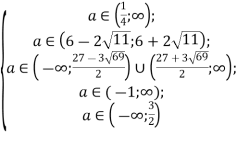
 Відповідь:

 Задача 7. За яких значень параметра а корені рівняння   є сторонами різностороннього трикутника периметра 2а?

 Розв′язання. Враховуючи нерівність трикутника, числа будуть сторонами трикутника периметра 2а, якщо

          

 Тобто ми маємо встановити, за яких значень параметра а дане рівняння має три різні дійсні додатні корені, менші за а,  

 

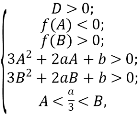
де

Тоді

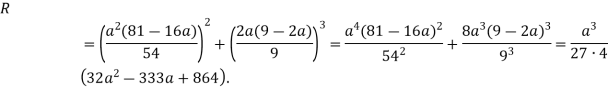
Повертаючись до системи, отримаємо

         

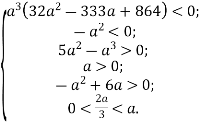
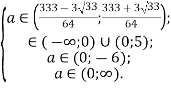
 Відповідь:  .

 Задача 8. Знайти всі значення параметра а, при яких рівняння

  має рівно 3 розв′язки на .

 Розв′язання. Якщо  , то , тому поділимо обидві частини рівняння на .

 Зробимо заміну , оскільки .

 Отримаємо рівняння , яке повинно мати три додатні корені, тобто мають виконуватися умови

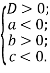
  Оскільки , то отримаємо

  

.

при , тобто при

. Повертаючись до системи, отримаємо

          .

 Відповідь: .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ВИСНОВКИ

 Дане дослідження навчило мене розв’язувати задачі з параметрами, застосовуючи властивості коренів кубічного рівняння. Звичайно, не можна стверджувати, що спосіб запропонований у даній роботі, є панацеєю для дослідження кубічних рівнянь і користуватися потрібно тільки ним. Але знання й уміння користуватися різними методами розширює математичний математичний кругозір, дає можливість швидше і більш раціонально розв′язувати задачі.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

1. А м е л ь к и н   В. В.,  Р а б ц е в и ч   В.  Л.  Задачи с праметрами:   Справ.   пособие по математике.  -  Мн. Асар,  1996.  -  464  с.
2. Б у к о в с ь к а  О. І. Тригонометрія: Параметри в завданнях з тригонометричними функціями:  Навч.-метод. посібник.  -  К.:  ПЛ  НТУУ  ″КПІ″,  2005.  -  120 с.
3. З а в а л о  С. Т., К о с т а р ч у к  В. М., Х а ц е т  Б. І. Алгебра  і  теорія  чисел.  -  К.: Вища шк.,  1974.  -  464 с.
4. Р е п е т а  В. К. та ін. Задачі з параметрами:  Навч. посібник.  -  К.:  Вища  шк.,  2006.  -  302 с.
5. С а р а н а  О.  А.  Математичні олімпіади:  просте  і  складне  поруч:  Навч.  посібник.  -  К.:  А.С.К.,  2005.  -  344 с.
6. Я с і н с ь к и й  В.  В.  Математика.  Навчальний  посібник  для  слухачів  ІДП  НТУУ  ″КПІ″.  -  К.:  НТУУ  ″КПІ″,  2004.  -  400 с.