Навчальний кейс/завдання з теми: "Суміжні та вертикальні кути, їх властивості"

Навчальний предмет: Математика
Навчальна тема: "Суміжні та вертикальні кути "
Тема уроку: "Суміжні та вертикальні кути та їх властивості"

Формулювання навчального кейсу/завдання

Учні створюють серію завдань, які демонструють властивості суміжних та вертикальних кутів, використовуючи генеративний ШІ, наприклад, ChatGPT та Gemini. Завдання можуть бути представлені як частина презентації, звіту або інтерактивного постера.

Завдання для учнів:

1. Створити по одному завданню для суміжних та вертикальних кутів, пояснюючи їх властивості.
2. Підготувати короткий зміст завдання, як ілюструється, і пояснити, як воно пов'язане з відповідними властивостями.
3. Оформити свої роботи у вигляді електронного документа чи слайдів для презентації.

Як використовувати сервіс ШІ

1. Учитель демонструє, як працює генеративний ШІ, використовуючи, наприклад, ChatGPT та Gemini для створення завдань. Для прикладу, вводить промт: «Створи завдання для застосування властивостей суміжних та вертикальних кутів»
2. Учні формулюють власні промти для створення завдань для кожного рівня. Наприклад:

• Початковий рівень: "Що таке суміжні кути, вертикальні кути"
• Середній рівень: "Створи завдання для середнього рівня"
• Достатні рівень: "Створи завдання достатнього рівня використовуючи властивості суміжних та вертикальних кутів".
• Високий рівень: «Створи завдання дослідницького рівня із теми Суміжні та вертикальні кути»

3. Учні використовують створені ілюстрації для підготовки міні-презентацій або звітів, пояснюючи кожен приклад.

Як це допоможе досягти навчальних цілей уроку

• Розвинуть навички роботи з сучасними цифровими технологіями (генеративним ШІ).
• Розвинуть критичне мислення, аналізуючи, наскільки результати ШІ відповідають реальності.
• Отримають візуальні матеріали, які допоможуть краще зрозуміти теоретичні знання.
• Використання сучасних технологій (генеративного ШІ) допомагає інтегрувати цифрові навички у навчальний процес.
• Розвиток презентаційних навичок через демонстрацію робіт.

Згенеровані завдання та промти для ШІ

Початковий рівень Суміжні та вертикальні кути: просте пояснення

Суміжні куті та вертикальні куті – це важливі поняття у геометрії, які часто зустрічаються при розв'язанні завдань. Давайте розглянемо їх детальніше.

Суміжні куті

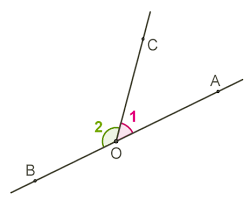
• Двоє кутів називаються суміжними, якщо вони мають одну спільну сторону, а дві інші сторони є продовженням одна одної.
• Сума мір суміжних кутів завжди дорівнює 180 градусів.
• Уявления: Уяви собі пряму лінію, розділену на дві частини іншою прямою.

Відкриється у новому вікніwww.miyklas.com.ua

суміжні куті

Вертикальні куті

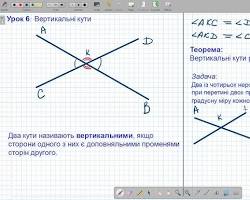
• Визначення: Два кутки називаються вертикальними, якщо сторони одного кута є продовженням сторін іншого куточка.
• Вертикальні куті завжди рівні між собою.
• Коли дві прямі перетинаються , утворюються чотири куті. Шкіра пара протилежних кутів є парою вертикальних кутів.

Відкриється у новому вікніwww.youtube.com

вертикальні куті

Чому це важливо?

Розуміння суміжних та вертикальних кутів є ключовим для розв'язання багатьох геометричних завдань. Ці знання допомагають:

• Знаходити невідомі куті на малюнках.
• Доводити різноманітні геометричні твердження.
• Виконувати побудови за допомогою циркуля та лінійки.

Приклад завдання:

• Якщо один із суміжних кутів дорівнює 70 градусів, то якою буде міра іншого угла?
• Відповідь: 180 градусів – 70 градусів = 110 градусів.

Поради для кращого розуміння:

• Рисунки: Завжди малюйте схематичні зображення кутів, щоби краще візуалізувати їх взаємне розташування.
• Практика: Розв'язуйте якнайбільше завдань на знаходження суміжних та вертикальних кутів.
• Запам'ятайте основні властивості: Сума суміжних кутів дорівнює 180 градусів, а вертикальні куті рівні.

Завдання середнього рівня на тему "Суміжні та вертикальні куті"

Теоретичні запитання:

1. Визначення: Дайте визначення суміжних та вертикальних кутів.
2. Які основні властивості мають суміжні та вертикальні куті?
3. Відмінності: Чим відрізняються суміжні куті від вертикальних?
4. Приклад: Наведіть приклад реальної ситуації, де можна побачити суміжні та вертикальні куті (наприклад, годинники, двері, перехрестя).

Практичні завдання:

1. Знаходження невідомих кутів:
   • На малюнку зображено два суміжні куті. Один із них дорівнює 125°. Знайдіть міру іншого кута.
   • Два вертикальні кути позначені як x і 3x-20°. Складіть рівняння та знайдіть значення x.
2. Доведення рівності кутів:
   • Доведіть, що якщо два куті є вертикальними, то вони рівні.
   • На малюнку зображено чотири прямі, які перетинаються в одній точці. Доведіть, що сума всіх чотирьох кутів дорівнює 360°.
3. Розв'язання задач з текстовим описом:
   • Два куті утворюють розгорнутий кут. Один із них на 30° більший за інший. Знайдіть міру шкірного кута.
   • На перехресті доріг утворилися чотири куті. Один із них дорівнює 75°. Знайдіть міри всіх інших кутів.
4. Побудова кутів:
   • За допомогою транспортира побудуйте два суміжні кути, один з яких дорівнює 110°.
   • Побудуйте дві прямі, які перетинаються під прямим кутом. Позначте всі утворені куті і вкажіть, які з них є суміжними, а які вертикальними.

Додамо візуалізації до завдань високого рівня.

Завдання 1: Доведіть, що якщо дві прямі перпендикулярні, то всі куті, утворені при їх перетині, прямі.

Відкриється у новому вікніwww.studypug.com

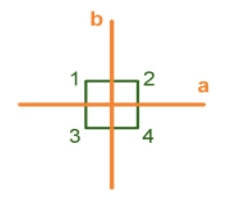
дві перпендикулярні лінії intersecting, forming four right angles

Роз'яснення до малюнку:

• Дві прямі a і b перетинаються під прямим углом (позначено квадратиком).
• Утворені чотири куті позначені цифрами від 1 до 4.
• За умовою задачі, кут 1 – прямий.
• Нам потрібно довести, що куті 2, 3 і 4 також прямі.

Завдання 2: Сума двох суміжних кутів дорівнює 3x+20. Знайдіть значення x, якщо один з кутів на 10° більший за інший.

Відкриється у новому вікніthirdspacelearning.com

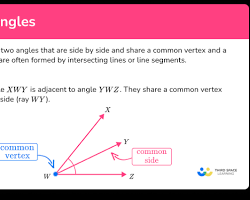
два adjacent angles, один labeled як x, інші як x+10

Роз'яснення до малюнку:

• Два куті, позначені x і x+10, мають спільну сторону і утворюють розгорнутий угол (180 градусів).
• Нам потрібно скласти рівняння та знайти значення x.

Завдання 2: Два вертикальні куті відносяться як 2:3. Знайдіть міру шкірного угла.

Відкриється у новому вікніwww.youtube.com

Роз'яснення до малюнку:

• Два куті, позначені 2y і 3y, є вертикальними, тобто рівні між собою.
• Їх відношення дорівнює 2:3, що означає, що один кут становить 2 частини від цілого, а інший - 3 частини.
• Нам потрібно знайти загальну кількість частин і визначити, скільки градусів припадає на одну частину.

Додаткові поради щодо використання малюнків:

• Чіткість: Малюнки мають бути зрозумілими та чіткими, щоб учень легко міг зорієнтуватися в умові задачі.
• Позначення: Всі елементи рисунка (куті, відрізки, прямі) повинні бути чітко позначені літерами чи цифрами.
• Колір: Використання кольору може допомогти виділити важливі елементи малюнку.
• Динаміка: Якщо це можливо, створіть анімаційні або інтерактивні малюнки, щоб зробити процес навчання цікавішим.

Онлайн-інструменти для створення малюнків:

• GeoGebra: потужний інструмент створення геометричних конструкцій.
• Desmos: онлайн-калькулятор, який також дозволяє будувати графіки функцій.
• Google Drawings: простий у використанні інструмент для створення діаграм і малюнків.

Завдання з малюнками стануть більш зрозумілими та цікавими для учнів, а також допоможуть їм краще засвоїти матеріал.

Завдання дослідницького рівня з теми "Суміжні та вертикальні куті"

Завдання 1: Історичний аспект

• Мета: Вивчити історію виникнення зрозуміти "суміжний кут" та "вертикальний кут". Які вчені зробили найбільший внесок у розвиток цих зрозуміти? Як ці поняття використовувалися у різних цивілізаціях (давній Єгипет, Греція, Китай)?
• Завдання:
  • Провести дослідження історичних джерел (стародавні манускрипти, трактати, архітектурні пам'ятки).
  • З'ясувати, як змінювалося розуміння суміжних та вертикальних кутів з годиною.
  • Порівняти термінологію та позначення, які використовувалися у різних культурах.
  • Створити презентацію чи есе, в якому викласти результати дослідження.

Завдання 2: Застосування в архітектурі

• Мета: Проаналізувати, як поняття суміжних та вертикальних кутів застосовуються у сучасній архітектурі.
• Завдання:
  • Вибрати кілька відомих архітектурних споруд та проаналізувати їх геометричні особливості.
  • З'ясувати, як архітектори використовують знання про куті для створення естетичних та функціональних будівель.
  • Створити модель або креслення будинку, в якому продемонструвати застосування суміжних та вертикальних кутів.

Завдання 3: Кути в природі

• Мета: Дослідити, як поняття кутів виявляється у природі.
• Завдання:
  • Вивчити наукові статті та дослідження про геометрію в природі.
  • Знайти приклади суміжних та вертикальних кутів у рослинному та тваринному світі (наприклад, будова крила метелика, розташування листків на стеблі).
  • Створити фотоальбом чи відеоролик, у якому продемонструвати знайдені приклади.

Завдання 4: Кути в мистецтві

• Мета: Вивчити використання кутів у образотворчому мистецтві.
• Завдання:
  • Проаналізувати картини відомих художників, звернувши увагу на те, як вони використовують куті для створення композиції та передачі емоцій.
  • Створити власну картину, в якій свідомо використовуватимуться суміжні та вертикальні куті.

Завдання 5: Кути у програмуванні

• Мета: Дослідити, як поняття кутів застосовується у програмуванні для створення графіки та анімації.
• Завдання:
  • Вивчити основи мови програмування (наприклад, Python, Scratch).
  • Створити програму, яка будує різні фігури з використанням суміжних та вертикальних кутів.
  • Анімувати рух об'єктів, змінюючи куті їх повороту.

Завдання 6: Кути у спорті

• Мета: Проаналізувати, як поняття кутів використовується у різних видах спорту.
• Завдання:
  • Вибрати вид спорту, який вас цікавить, та проаналізувати техніку виконання різних рухів.
  • З'ясувати, як зміна кута впливає на результативність спортсмена.
  • Створити відеоролик, в якому продемонструвати роль кутів у вибраному виді спорту.

Критерії оцінювання:

• глибина дослідження.
• Оригінальність підходу.
• Якість оформлення роботи.
• Уміння аналізувати та узагальнювати інформацію.
• Здатність до самостійної роботи.

Додаткові поради:

• Заохочуйте учнів до використання різних джерел інформації (підручники, наукові статті, інтернет-ресурси, бібліотеки).
• Надавайте учням можливість обирати теми дослідження відповідно до їх інтересів.
• Запросіть фахівців з різних галузей для проведення консультацій.
• Організуйте презентації результатів досліджень.

Ці завдання дозволять учням  не лише закріпити знання про суміжні та вертикальні куті, але й розвинути такі навички як:

• Дослідницька діяльність.
• Критичне мислення.
• Творчість.
• Міжпредметні зв'язки.

Бажаю успіхів у дослідницькій роботі!