Навчальний посібник "Алгебра 9 клас І семестр"
Посібник розроблений згідно Комбінованої системи М.П. Гузика і може бути використані як додатковий матеріал для учнів на уроки. Кожна тема помсібника має таку структуру:
- перший урок – урок розбору блоку навчальної інформації;
- наступні уроки – уроки фронтального опрацювання матеріалу,
- між уроками фронтального опрацювання містяться завдання по підготовці до уроків індивідуального опрацювання матеріалу;
- в кінці кожної теми є один урок внутрішньопредметного узагальнення матеріалу, на якому кожен продемонструє свої знання блоку, а також узагальнить знання і вміння, здобуті під час теми.
Ківерцівська експериментальна школа
Навчальний посібник

І семестр

Шановні учні!!!
Ви продовжуєте вивчати одну з найважливіших математичних дисциплін – алгебру. Допоможе вам у цьому посібник, який ви тримаєте в руках.
Він містить уроки розбору блоку навчального матеріалу, уроки фронтального опрацювання матеріалу та уроки внутрішньопредметного узагальнення матеріалу.
 Перевірити свої знання і підготуватись до індивідуального опрацювання матеріалу можна, виконавши завдання у рубриці «Готуємось до індивідуального опрацювання матеріалу», позначеного
Перевірити свої знання і підготуватись до індивідуального опрацювання матеріалу можна, виконавши завдання у рубриці «Готуємось до індивідуального опрацювання матеріалу», позначеного
Якщо ви пропустите один або кілька уроків з алгебри, опрацюйте матеріал цих уроків вдома.
Бажаю успіхів у вивченні алгебри!!!
Блок №1. Числові нерівності
Урок №1

Числові нерівності
«Для всього свій час, і година
своя кожній справі під небом»
Книга Еклезіаста 3:1
Питання
- Числові нерівності.
- Властивості числових нерівностей.
- Додавання і множення числових нерівностей. Оцінювання значення виразу.
Література
Істер О.С. Алгебра: Підручник для 9 класу, §1 – 3, стор. 5 – 29.
|
1. Числові нерівності та їх властивості |
||
|
1.1 |
Два вирази, сполучені знаком нерівності ( |
|
|
1.2 |
|
|
|
1.3 |
Нерівність, обидві частини якої є числа, називають числовою нерівністю. |
|
|
1.4 |
Число а вважають більшим за число b, якщо різниця а – b є додатним числом. |
|
|
1.5 |
Число а вважають меншим за число b, якщо різниця а – b є від’ємним числом. |
|
|
1.6 |
Числа а і b вважають рівними, якщо різниця а – b дорівнює 0. |
|
|
2. Властивості числових нерівностей |
||
|
2.7 |
Якщо |
|
|
2.8 |
Якщо до обох частин правильної нерівності додати або від обох частин правильної нерівності відняти одне й те саме число, то отримаємо правильну нерівність. |
Якщо
|
|
2.9 |
Якщо будь-який доданок перенести з однієї частини правильної нерівності в другу, змінивши знак доданка на протилежний, то тримаємо правильну нерівність. |
|
|
2.10 |
Якщо обидві частини правильної нерівності помножити або поділити на одне й те саме додатне число, то отримаємо правильну нерівність.
|
|
|
2.11 |
Якщо обидві частини правильної нерівності помножити або поділити на одне й те саме від’ємне число і замінити знак нерівності на протилежний, то отримаємо правильну нерівність. |
|
|
3. Додавання і множення числових нерівностей. Оцінювання значення виразу |
||
|
3.12 |
При почленному додаванні правильних нерівностей одного знака результатом є правильна нерівність того самого знака. |
|
|
3.13 |
При почленному множенні правильних нерівностей одного знака, у яких ліві і праві частини – додатні числа, результатом є правильна нерівність того самого знака. |
то |
|
3.14 |
Якщо |
|
|
3.15 |
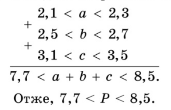
Якщо відомо значення меж величин, то використовуючи властивості числових нерівностей, можна знайти межі значення виразу, який містить ці величини, тобто оцінити його значення. |
|
Урок №2
«Без бажання все важке, навіть найлегше»
Григорій Сковорода
Фронтальне опрацювання матеріалу
Числові нерівності. Основні властивості числових нерівностей
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 2.11 блоку № 1.
- Усно дай відповідь на питання:
- Що називають нерівністю?
- Які бувають нерівності?
- Які нерівності називають числовими?
- Сформулюй правила порівняння чисел.
-
Якщо
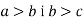
- Сформулюй правило додавання, віднімання числа до обох частин нерівності.
- Сформулюй правило перенесення доданка з однієї частини нерівності в іншу.
- Сформулюй правило множення або ділення нерівності на додатне число.
- Сформулюй правило множення або ділення нерівності на від’ємне число.
Завдання 2.
Усно виконай вправи 1; 3, стор. 9.
ІІ. Відпрацювання умінь і навичок розв’язування вправ
Завдання 3.
- Прочитайте історичну довідку на стор. 8, 9.
- Письмово виконай вправи, стор. 10 підручника: 12, 18.
Завдання 4.
Письмово виконай вправи, стор. 18 – 19 підручника: 47; 58; 60.
Уроки №3, 4
«Без бажання все важке, навіть найлегше»
Григорій Сковорода
Фронтальне опрацювання матеріалу
Додавання і множення нерівностей. Оцінювання значення виразу

І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 3.15 блоку № 1.
- Усно дай відповідь на питання:
- Що називають нерівністю?
- Які бувають нерівності?
- Які нерівності називають числовими
- Сформулюй правила порівняння чисел.
-
Якщо
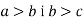
- Сформулюй правило додавання, віднімання числа до обох частин нерівності.
- Сформулюй правило перенесення доданка з однієї частини нерівності в іншу.
- Сформулюй правило множення або ділення нерівності на додатне число.
- Сформулюй правило множення або ділення нерівності на від’ємне число.
- Сформулюй правило додавання нерівностей.
- Сформулюй правило множення нерівносте.
- Сформулюй правило піднесення нерівностей до степеня.
- Як оцінити значення виразу?
Завдання 2.
Усно виконай вправу

ІІ. Відпрацювання умінь і навичок розв’язування вправ
Завдання 3.


Завдання 4.
4.1. Підприємство виготовляє газонну страву у вигляді килимків прямокутної форми. Ширина такого прямокутника становить ![]()
![]()
![]() прямокутника, якщо
прямокутника, якщо ![]()
4.2. Маса m однієї шоколадної цукерки набуває значень ![]()
4.3. Для закупівлі навчальних посібників планується виділити від 950 до 1100 грн. Вартість одного посібника становить 60 грн.
а) Скільки посібників можна купити на заплановану суму?
б) Яку найбільшу кількість посібників можна купити на заплановану суму, якщо вартість одного посібника збільшиться на 10 %?
Завдання 5.
Письмово виконай вправи, стор. 26, 27 підручника: 93, 95, 97, 102 (1, 3).
ІІІ. Відпрацювання умінь розв’язування нестандартних вправ та задач
Завдання 6.
Письмово виконай вправу
ЗАДАЧА «НАПИС НА ЕТИКЕТЦІ»
Етикетка на 6-літровому бутлі мінеральної негазованої води має напис: «Об’єм 6 ![]() ±1%».
±1%».
1. Нехай у такому закоркованому бутлі міститься V л води. Ураховуючи напис на його етикетці, оцініть значення V.
2. Для учасників олімпіади слід замовити 596 л цієї води. Було закуплено 50 упаковок, у кожній — два 6-літрові бутлі.
1) Оцініть значення об’єму закупленої води (у л).
2) З’ясуйте, чи достатньо води було закуплено.
 Готуємось до індивідуального опрацювання матеріалу
Готуємось до індивідуального опрацювання матеріалу
-
Порівняй числа a і b, якщо
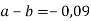
-
Відомо, що
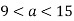
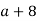
-
Оціни периметр і площу прямокутника зі сторонами
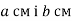
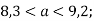
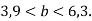
-
Доведи нерівність:
 .
.
-
Доведи, що сума двох обернених додатних чисел не менша від числа 2:
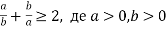 .
.
Урок №6
«Ми знаємо, хто ми є, але не знаємо,
ким ми можемо бути»
Вільям Шекспір
Внутрішньопредметне узагальнення матеріалу
Числові нерівності
І. Систематизація та узагальнення теоретичних знань
Завдання 1.
- Повтори блок № 1.
- Дай письмово відповідь на питання , запропоновані вчителем.
Завдання 2.
Усно виконай вправи:
-
Яка з наведених нерівностей правильна, якщо
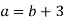
|
А |
Б |
В |
Г |
|
|
|
|
Визначити неможливо |
-
Серед наведених нерівностей виберіть ту, яка утвориться, якщо до обох частин нерівності
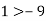
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Серед наведених нерівностей виберіть ту, яка утвориться, якщо обидві частини нерівності
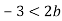
|
А |
Б |
В |
Г |
|
|
|
|
|
ІІ. Систематизація та узагальнення практичних умінь та навичок
Завдання 3.
Письмово виконай вправи:
-
Додай почленно нерівності
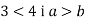
-
Перемнож почленно нерівності
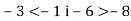
-
Відомо, що
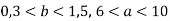
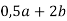
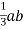 .
.
-
Доведи нерівність:
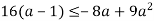 .
.
Блок №2. Нерівності із змінними. Розв’язування лінійних нерівностей та їх систем
Урок №1

Нерівності із змінними. Розв’язування лінійних нерівностей та їх систем
«У самій математиці головні засоби
досягти істини – індукція та аналогія»
П. Лаплас
Питання
- Нерівності зі змінними. Розв’язок нерівності. Числові проміжки.
- Розв’язування лінійних нерівностей з однією змінною.
- Розв’язування систем лінійних нерівностей.
- Розв’язування подвійних нерівностей.
Література
Істер О.С. Алгебра: Підручник для 9 класу, §4 – 7, стор. 29 – 67.
|
1. Нерівності зі змінними. Розв’язок нерівності. Числові проміжки |
|||
|
1.1 |
Нерівність, яка містить невідоме, називають нерівністю зі змінною. |
|
|
|
1.2 |
Розв'язком нерівності з однією змінною називають значення змінної, яке перетворює її у правильну числову нерівність. |
||
|
1.3 |
Розв'язати нерівність означає знайти всі її розв'язки, або довести, що їх немає |
||
|
1.4 |
Усі розв'язки нерівності утворюють множину розв'язків нерівності. |
||
|
1.5 |
Якщо нерівність розв'язків немає, то кажуть, що множиною її розв'язків є порожня множина – |
||
|
1.6 |
Дві нерівності називаються рівносильними, якщо вони мають одну й ту саму множину розв’язків. |
і |
|
|
1.7 |
Множину розв'язків нерівності називають числовим проміжком. |
||
|
1.8 |
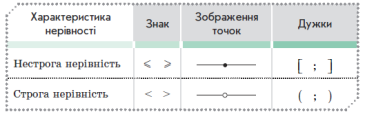
Якщо точки – кінці проміжку включені в проміжок, то для запису використовують квадратні дужки, якщо не включені – круглі дужки. |
||
|
2. Розв’язування лінійних нерівностей |
|||
|
2.9 |
Нерівності виду |
||
|
2.10 |
Властивості, які використовуються під час розв’язування нерівностей:
|
||
|
3. Розв’язування систем лінійних нерівностей |
|||
|
3.11 |
Якщо необхідно знайти спільні розв’язки двох чи більше нерівностей, то говорять, що треба розв’язати систему нерівностей. |
|
|
|
3.12 |
Розв’язком системи нерівностей з однією змінною називають значення змінної, при якому правильною є кожна з нерівностей системи. |
||
|
3.13 |
Розв’язати систему нерівностей з однією змінною означає знайти всі її розв’язки або довести їх немає. |
||
|
3.14 |
Схема розв’язування систем нерівностей
|
||
|
4. Розв’язування подвійних нерівностей |
|||
|
4.15 |
Щоб розв’язати подвійну нерівність потрібно записати її у вигляді системи двох нерівностей і розв’язати цю систему. |
||
Урок №2
«Прекрасне осягається шляхом вивчення і великих зусиль,
погане засвоюється само собою, без праці»
Демокріт
Фронтальне опрацювання матеріалу
Нерівності зі змінними. Розв’язок нерівності
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 1.6 блоку № 2.
- Усно дай відповідь на питання:
- Що називають нерівністю зі змінною?
- Що означає розв’язати нерівність?
- Що називають розв’язком нерівності?
- Які нерівності називаються рівносильними?
- Що називають порожньою множиною і як її позначають?
Завдання 2.
Усно виконай вправи 115, 117 на ст. 30.
ІІ. Відпрацювання умінь і навичок розв’язування вправ
Завдання 3.
- Письмово виконай вправи, стор. 30 підручника: 123, 124, 126 (1, 3, 5, 7, 9).
- Самостійно визнач, чи є задане число розв’язком нерівності:
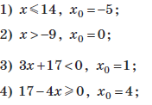
ІІІ. Відпрацювання умінь розв’язування нестандартних вправ та задач
Завдання 4.

Урок №3
«Почніть робити те, що потрібно.
Потім робіть те, що можливо.
І ви раптом виявите, що робите неможливе»
Св. Франциск Асізський
Фронтальне опрацювання матеріалу
Числові проміжки
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 1.8 блоку № 2.
- Усно дай відповідь на питання:
- Що називають нерівністю зі змінною?
- Що означає розв’язати нерівність?
- Що називають розв’язком нерівності?
- Які нерівності називаються рівносильними?
- Що називають порожньою множиною і як її позначають?
- Що називають числовим проміжком?
- Поясніть як позначають точки на проміжку, і від чого залежить написання дужок.
Завдання 2.
Усно виконай вправи
2.1. Правильно прочитайте числові проміжки
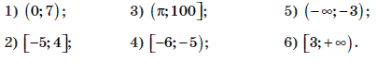
2.2. Визначте, чи належить проміжку ![]() число
число
![]()
ІІ. Відпрацювання умінь і навичок розв’язування вправ
Завдання 3.
3.1. Із §5 стор. 34 – 35 випиши означення перерізу та об’єднання числових проміжків.
3.2. Письмово виконай вправи, стор. 37, 38 підручника: 148, 152, 158, 160.
ІІІ. Відпрацювання умінь розв’язування нестандартних вправ та задач
Завдання 4.
Визначте зміст повідомлень, які отримують учасники дорожнього руху з наведених дорожніх знаків. Уведіть необхідні буквені позначення та спробуйте записати ці повідомлення за допомогою нерівностей.

Урок №4
«Хай з любов'ю все робиться в вас!»
1 послання ап. Павла до коринтян 16:14
Фронтальне опрацювання матеріалу
Лінійні нерівності з однією змінною
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 2.10 блоку № 2.
- Усно дай відповіді на запитання:
- Що називають лінійною нерівністю?
- Що називають числовими проміжком?
- Які нерівності називаються рівносильними?
- Назви властивості, які використовуються для розв’язування нерівностей.
- Що означає розв’язати нерівність?
- Що називають перерізом числових проміжків?
- Що називають об’єднанням числових проміжків?
Завдання 2.
Усно розгляньте приклади розв’язування нерівностей і порівняйте ці розв’язання:

Завдання 3.
Усно виконайте вправу:
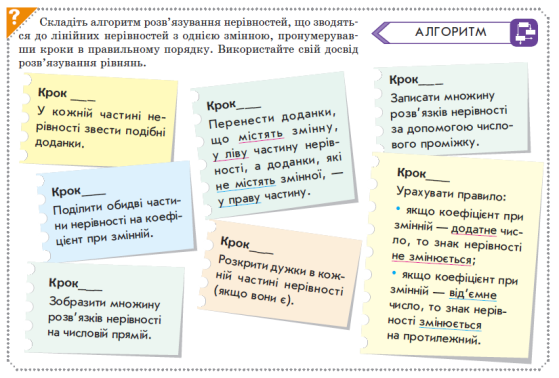
ІІ. Відпрацювання умінь і навичок розв’язування вправ
Завдання 3.
Письмово виконай вправи, стор. 44 – 46 підручника: 178, 184, 202, 206 (1, 3).
ІІІ. Відпрацювання умінь розв’язування нестандартних вправ та задач
Завдання 4.
В автомобіль слід завантажити спочатку 5 ящиків з яблуками, а потім – мішки з цукром. Маса одного ящика з яблуками дорівнює 35 кг, одного мішка з цукром – 50 кг. Яку найбільшу кількість мішків із цукром можна завантажити в автомобіль, якщо загальна маса вантажу не має перевищувати 2 т?
Уроки №5, 6
«Доброта – це любов, що
виливається з лагідного серця»
Народна мудрість
Фронтальне опрацювання матеріалу
Розв’язування систем лінійних нерівностей. Розв’язування подвійних нерівностей
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори блок № 2.
- Усно дай відповіді на запитання:
- Що називають лінійною нерівністю?
- Що називають числовими проміжком?
- Які нерівності називаються рівносильними?
- Що таке система лінійних нерівностей?
- Що називають розв’язком системи?
- Назвіть схему розв’язування системи лінійних нерівностей.
- Як розв’язати подвійну нерівність?
Завдання 2.
2.1. Усно розгляньте приклад розв’язування вправи:

2.2. Усно виконайте вправи, запропоновані вчителем у презентації.
ІІ. Відпрацювання умінь і навичок розв’язування вправ
Завдання 3.
3.1. Виконайте економічну задачу, наведену у презентації вчителем.
3.2. Письмово виконай вправи, стор. 52 – 56 підручника: 228, 232, 235 (1, 3), 238, 244, 247, 250, 253.

ІІІ. Відпрацювання умінь розв’язування нестандартних вправ та задач
Завдання 4.
Виконайте завдання «Перерва на логіку»
 Готуємось до індивідуального опрацювання матеріалу
Готуємось до індивідуального опрацювання матеріалу
-
Записати множину розв’язків подвійної нерівності
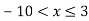
-
Розв’язати нерівність
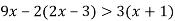
-
Розв’язати систему нерівностей
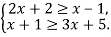
-
Розв’язати подвійну нерівність
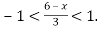
- Позашляховик за 6 год долає по гірській дорозі більше ніж 180 км, а по шосе за 4 год — не більше ніж 440 км.
а) Складіть систему нерівностей для визначення швидкості v (у км/год) позашляховика протягом поїздки.
б) У яких межах змінюється ця швидкість?
-
Знайти множину цілих розв’язків системи
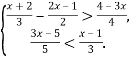
Урок №8
«Ми прийшли в цей світ, щоб допомагати
один одному в нашій подорожі по життю»
Уїльям Джеймс, американський психолог і філософ
Внутрішньопредметне узагальнення
Розв’язування лінійних нерівностей та систем лінійних нерівностей
І. Систематизація та узагальнення теоретичних знань
Завдання 1.
- Повтори блок № 2.
- Дай письмово відповідь на питання, запропоновані вчителем.
Завдання 2.
Усно виконай вправи:
-
Множину розв’язків нерівності
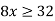
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Розв’язком системи нерівностей
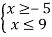 є числовий проміжок
є числовий проміжок
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Вкажіть найменше ціле число, яке задовольняє умову
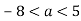
|
А |
Б |
В |
Г |
|
– 8 |
5 |
– 7 |
0 |
ІІ. Систематизація та узагальнення практичних умінь та навичок
Завдання 3.
Письмово виконай вправи:
-
Розв’язати нерівність
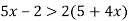
-
Розв’язати систему нерівностей
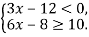
-
При яких значеннях a значення виразу
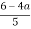 належить числовому проміжку [– 1;4].
належить числовому проміжку [– 1;4].
-
Знайдіть усі цілі розв’язки системи нерівностей
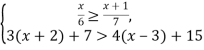
-
При яких значеннях
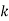
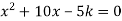 має два різні корені?
має два різні корені?
Блок №3. Функція. Властивості та графіки функцій. Квадратична функція
Урок №1

Функція. Властивості та графіки функцій. Квадратична функція
«Не дайте себе звести, –
товариство лихе псує добрі звичаї!»
1послання ап.. Павла до коринтян 15:33
Питання
- Функція. Область визначення. Область значень і графік функції
- Властивості функції.
- Перетворення графіка функції.
- Квадратична функція, її властивості і графік.
Література
Істер О.С. Алгебра: Підручник для 9 класу, §8 – 11, стор. 68 – 111.
|
1. Функція. Область визначення. Область значень і графік функції |
|||||||||||||||||||||||
|
1.1 |
Функція – це правило, за допомогою якого за кожним значенням незалежної змінної з множини Х можна знайти єдине значення залежної змінної У. |
||||||||||||||||||||||
|
1.2 |
Незалежну змінну називають аргументом функції і зазвичай позначають буквою |
||||||||||||||||||||||
|
1.3 |
Значення залежної змінної називають значенням функції і зазвичай позначають буквою |
||||||||||||||||||||||
|
1.4 |
Усі значення, яких набуває незалежна змінна (аргумент) називаються областю визначення функції. Позначення: D, D(y). |
D(y) = R |
|||||||||||||||||||||
|
1.5 |
Усі значення, яких набуває залежна змінна, називаються областю значень функції. Позначення: Е, Е(у) |
Е(у) = R |
|||||||||||||||||||||
|
1.6 |
Функцію можна задати одним з таких способів:
|
||||||||||||||||||||||
|
1.7 |
Графіком функції |
||||||||||||||||||||||
|
1.8 |
Основні види елементарних функцій і їх графіки
|
||||||||||||||||||||||
|
2. Властивості функції |
|||||||||||||||||||||||
|
2.9 |
Значення аргументу, при якому значення функції дорівнює нулю, називають нулем функції. |
|
|||||||||||||||||||||
|
2.10 |
Кожний з проміжків, на якому функція набуває значень одного знака, називаються проміжком знакосталості функції. |
|
|||||||||||||||||||||
|
2.11 |
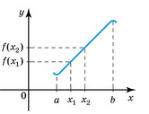
Функцію називають зростаючою на деякому проміжку, якщо більшому значенню аргументу з цього проміжку відповідає більше значення функції. |
|
|||||||||||||||||||||
|
2.12 |
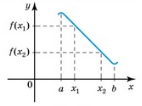
Функцію називають спадною на деякому проміжку, якщо більшому значенню аргументу з цього проміжку відповідає менше значення функції.
|
|
|||||||||||||||||||||
|
2.13 |
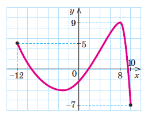
Найбільшим значенням функції називають найбільше число з області значень функції, а найменшим значенням функції – відповідно найменше число з області значень функції. |
9 – найбільше значення –7 – найменше |
|||||||||||||||||||||
|
3. Перетворення графіка функції |
|||||||||||||||||||||||
|
3.14 |
Графік функції
|
||||||||||||||||||||||
|
4. Квадратична функція, її властивості та графік |
|||||||||||||||||||||||
|
4.15 |
Функція, яку можна задати формулою виду |
|
|||||||||||||||||||||
|
4.16 |
Графіком квадратичної функції завжди є парабола, вітки якої напрямлені вгору при |
||||||||||||||||||||||
|
4.17 |
Координати вершини параболи:
Пряма |
||||||||||||||||||||||
|
4.18 |
Алгоритм побудови графіка квадратичної функції: 1) визначити напрям віток параболи; 2) обчислити координати вершини параболи; 3) знайти координати точок перетину параболи з осями координат:
а) з віссю абсцис: для цього розв’язуємо рівняння:
б) з віссю ординат: 4) обчислити значення функції ще у кількох точках; 5) позначити знайдені точки на координатній площині і з’єднати їх плавною лінією. |
||||||||||||||||||||||
Урок №2
«Любити все людство легше, ніж зробити
добро сусіду»
Г.Сковорода
 Фронтальне опрацювання матеріалу
Фронтальне опрацювання матеріалу
Функції
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 1.8 блоку №3.
- Дай відповіді на питання:
- Що таке функція?
- Що називають аргументом функції?
- Що називають областю визначення функції?
- Що називають областю значень функції?
- Що називають графіком функції?
- Розкажіть все, що ви знаєте про лінійну функцію.
-
Вкажіть, що є областю визначення, областю значень, графіком функції
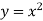 .
.
ІІ. Відпрацювання умінь і навичок, застосування правил
Завдання 2.
Усно виконайте вправи на стор. 72, 73: 327, 328.
Завдання 3.
3.1. Письмово виконайте вправи на стор. 73, 75: 334 (2, 4, 6), 346.
3.2. Побудуйте графік функції: ![]() .
.
3.3. Не виконуючи побудови, знайдіть координати точок перетину графіків функцій:
1) ![]()
2) ![]() .
.
ІІІ. Відпрацювання умінь розв’язування нестандартних вправ та задач
Завдання 4.
ЗАДАЧА «ВАНТАЖОПЕРЕВЕЗЕННЯ»
Транспортна компанія здійснює вантажоперевезення на відстань, не меншу від 20 км і не більшу за 50 км. Вартість перевезення вантажу на відстань від 20 до 30 км (не включаючи 30 км) становить 1000 грн, від 30 до 40 км (не включаючи 40 км) – 1200 грн, від 40 до 50 км –1400 грн.
1 Знайдіть область визначення функції y = f (x), де y – вартість (y грн) перевезення вантажу на відстань x (y км).
2 Побудуйте графік функції y = f (x), знайдіть область її значень.
3 Визначте вартість перевезення вантажу на відстань 43 км.
4 З’ясуйте:
- Чи може вартість перевезення вантажу дорівнювати 1350 грн;
- Чи можна перевезти вантажy на відстань 55 км.
Урок №3
«Алгебра та геометрія – єдині країни,
де панують тиша і мир»
Марія Аньєзі
Фронтальне опрацювання матеріалу
Властивості функцій
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 2.13 блоку №3.
- Дай відповіді на питання:
- Що називають функцією?
- Що називають нулями функції?
- Сформулюй означення графіка функції.
- Що називають проміжками знакосталості функції?
- Яку функцію називають зростаючою на проміжку?
- Яку функцію називають спадною на проміжку?
- Що називають найбільшим значенням функції?
- Що називають найменшим значенням функції?
-
Дай визнання області визначення і області значень функції.
- Усно виконай вправу. Яке поняття уроку розкриває дана вправа.
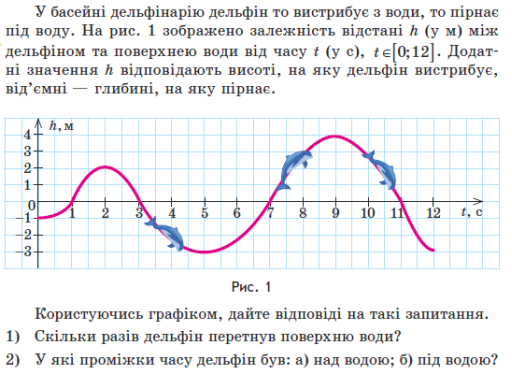
ІІ. Відпрацювання умінь і навичок, застосування правил
Завдання 2.
Усно виконайте вправи:
2.1.
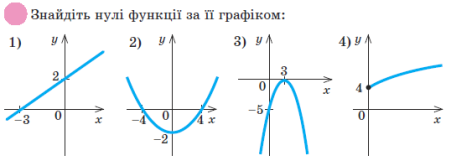
2.2.
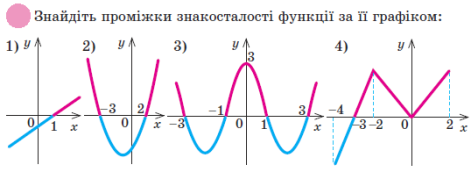
Завдання 3.
Письмово виконайте вправи на стор. 84 – 86: 367, 372 (1), 376 (1).
Уроки №4, 5
«Людина зроблена із книг, які вона читає»
Ральф Емерсон, американський есеїст, поет і філософ
Фронтальне опрацювання матеріалу
Найпростіші перетворення графіків функцій
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 3.14 блоку № 3.
- Усно дай відповіді на запитання:
- Що називають функцією?
- Як називаються значення незалежної і залежної змінної?
- Що називають областю визначення функції?
- Що називають областю значень функції?
- Які існують способи задання функції?
- Що називають нулем функції?
- Що називають проміжком знакосталості функції?
- Яка функція називається зростаючою на деякому проміжку?
-
Яка функція називається спадною на деякому проміжку?
- Розглянь приклади виконання найпростіших перетворень графіків функцій (презентація вчителя).
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Користуючись розглянутою презентацією та правилами, сформульованими у тезі 3.14 блоку № 3, виконай наступні завдання.
Завдання 2.
Усно виконай вправу, стор. 94 підручника: 389.
Завдання 3.
 Письмово виконай вправи 392, 396 (2, 4), 400 (2), 402, 403 стор. 94 – 96 підручника.
Письмово виконай вправи 392, 396 (2, 4), 400 (2), 402, 403 стор. 94 – 96 підручника.
ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач і вправ
Завдання 4.
Письмово виконай вправу
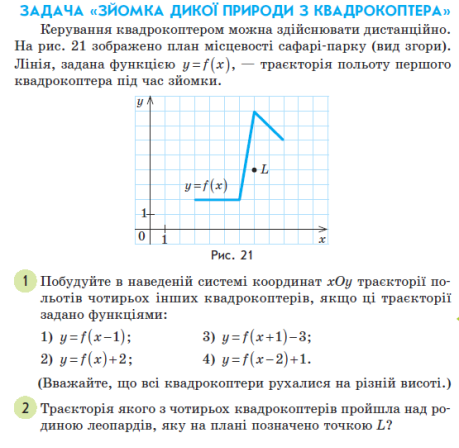
 Готуємось до індивідуального опрацювання матеріалу
Готуємось до індивідуального опрацювання матеріалу
-
Дано функцію
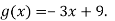 1) Знайди нулі функції; 2) порівняй
1) Знайди нулі функції; 2) порівняй 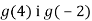 .
.
-
Функцію задано формулою
 . Знайди: 1)
. Знайди: 1) 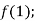 2)
2) 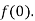
-
Знайди нулі функції
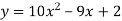 .
.
-
Побудуй графік функції
 .
.
Уроки №7, 8
«Одного разу ви зрозумієте, що ваша
велич починається там, де закінчується гординя»
Народна мудрість
Фронтальне опрацювання матеріалу
Квадратична функція, її графік та властивості
І. Робота над засвоєнням понять, термінів і правил
 Завдання 1.
Завдання 1.
- Повтори блок № 3.
- Усно дай відповіді на запитання:
- Що називають функцією?
- Як називаються значення незалежної і залежної змінної?
- Що називають областю визначення функції?
- Що називають областю значень функції?
- Які існують способи задання функції?
- Що називають нулем функції?
- Що називають проміжком знакосталості функції?
- Яка функція називається зростаючою на деякому проміжку?
- Яка функція називається спадною на деякому проміжку?
- Яка функція називається квадратичною?
- Що є графіком квадратичної функції?
- Як знайти координати вершини параболи?
- Як побудувати графік квадратичної функції?
Завдання 2.
- Усно виконай вправи, запропоновані вчителем у презентації.
- Усно виконай вправи:
- Яка з наведених функцій є квадратичною?
|
А |
Б |
В |
Г |
|
|
|
|
|
- Графіком якої з наведених функцій є парабола?
|
А |
Б |
В |
Г |
|
|
|
|
|
- У якої з парабол вітки напрямлені вниз?
|
А |
Б |
В |
Г |
|
|
|
|
|
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
- Письмово виконай вправи, стор. 105 підручника: 431, 436, 439 (1, 3).
-
Жонглер, стоячи на підлозі, підкидає м’ячик правою рукою і ловить лівою. Траєкторія польоту м’яча може бути змодельована графіком функції
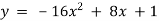 , де х — відстань (у м) по горизонталі від правої руки жонглера до м’яча, у — висота (у м), на яку піднімається м’ячик над підлогою.
, де х — відстань (у м) по горизонталі від правої руки жонглера до м’яча, у — висота (у м), на яку піднімається м’ячик над підлогою.
а) Побудуйте графік заданої функції, якщо ![]()
б) На яку найбільшу висоту підкидає м’ячик жонглер?
Завдання 4.
Письмово виконай вправи, стор. 106 підручника: 441, 444.
Завдання 5.
Письмово виконай вправи:
-
Знайти координати вершини параболи
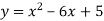 .
.
-
Знайти значення квадратичної функції
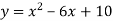 , якщо
, якщо 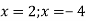
-
Знайти нулі квадратичної функції
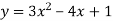 .
.
-
Графіку функції
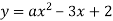 належить точка А(1; 3). Знайти коефіцієнт
належить точка А(1; 3). Знайти коефіцієнт 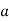
-
Побудувати графік функції
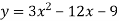 і за графіком встановити область значень функції, проміжки знакосталості та проміжки зростання і спадання функції.
і за графіком встановити область значень функції, проміжки знакосталості та проміжки зростання і спадання функції.
 Готуємось до індивідуального опрацювання матеріалу
Готуємось до індивідуального опрацювання матеріалу
-
Знайди координати вершини параболи
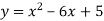 .
.
-
Знайди значення квадратичної функції
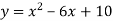 , якщо
, якщо 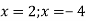
-
Знайди нулі квадратичної функції
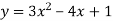 .
.
-
Графіку функції
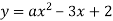 належить точка А(1; 3). Знайди коефіцієнт
належить точка А(1; 3). Знайди коефіцієнт 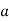
-
Побудуй графік функції
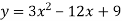 і за графіком встанови область значень функції, проміжки знакосталості та проміжки зростання і спадання функції.
і за графіком встанови область значень функції, проміжки знакосталості та проміжки зростання і спадання функції.
Урок №10
«Математику неможливо вивчати,
спостерігаючи, як це робить сусід!»
Айвен Нівен, американський математик
Внутрішньопредметне узагальнення матеріалу
Функції. Властивості та графіки функцій. Квадратична функція
І. Систематизація та узагальнення теоретичних знань
Завдання 1.
- Повтори блок № 3. Особливу увагу зверни на тези: 1.1; 1.5; 1.6; 1.7; 1.8; 2.10; 2.11; 2.12; 2.13; 4.15; 4.16; 4.17.
- Дай письмово відповідь на питання, запропоновані вчителем.
Завдання 2.
Усно виконай вправи:
-
Областю визначення функції
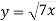 є…
є…
|
А |
Б |
В |
Г |
|
Всі дійсні числа |
|
Числа 0 і 1 |
|
-
Графік функції
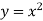 перенесли вгору на 3 одиниці. Якою формулою задається функція, графік якої отримали?
перенесли вгору на 3 одиниці. Якою формулою задається функція, графік якої отримали?
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Графік функції
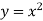 перенесли вліво на 3 одиниці. Якою формулою задається функція, графік якої отримали?
перенесли вліво на 3 одиниці. Якою формулою задається функція, графік якої отримали?
|
А |
Б |
В |
Г |
|
|
|
|
|
- Яка з наведених функцій є квадратичною?
|
А |
Б |
В |
Г |
|
|
|
|
|
ІІ. Систематизація та узагальнення практичних умінь та навичок
Завдання 3.
Письмово виконай вправи:
-
Дано функцію
 . Знайди
. Знайди 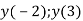 .
.
-
Знайди координати вершини параболи
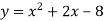 .
.
-
В одній системі координат побудуй графіки функцій:
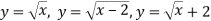 .
.
-
Графіку функції
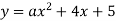 належить точка А (1; 2). Знайди коефіцієнт
належить точка А (1; 2). Знайди коефіцієнт 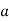
-
Побудуй графік функції
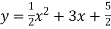 . За графіком встанови: 1) область значень функції; 2) проміжки зростання і спадання функції; 3) проміжки знакосталості функції.
. За графіком встанови: 1) область значень функції; 2) проміжки зростання і спадання функції; 3) проміжки знакосталості функції.
Повторення матеріалу, вивченого протягом І семестру
Урок №1
«Найважливіше завдання цивілізації –
навчити людину мислити»
Томас Едісон
Внутрішньопредметне узагальнення матеріалу
Узагальнення матеріалу, вивченого у І семестрі
І. Систематизація та узагальнення теоретичних знань
Завдання 1.
- Повтори блоки № 1 – 3.
- Дай відповіді на питання:
- Що називають нерівністю?
- Які бувають нерівності?
- Які нерівності називають числовими?
- Що називають лінійною нерівністю?
- Що називають числовими проміжком?
- Які нерівності називаються рівносильними?
- Що таке система лінійних нерівностей?
- Назвіть схему розв’язування системи лінійних нерівностей.
- Як розв’язати подвійну нерівність?
- Що називають функцією?
- Як називаються значення незалежної і залежної змінної?
- Що називають областю визначення функції?
- Що називають областю значень функції?
- Що називають нулем функції?
- Яка функція називається квадратичною?
- Що є графіком квадратичної функції?
- Як знайти координати вершини параболи?
- Як побудувати графік квадратичної функції?
Завдання 2.
Усно виконати вправи:
-
Серед наведених нерівностей виберіть ту, яка утвориться, якщо обидві частини нерівності
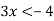
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Множину розв’язків нерівності
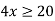
|
А |
Б |
В |
Г |
|
|
|
|
|
- Яка з наведених функцій є квадратичною?
|
А |
Б |
В |
Г |
|
|
|
|
|
ІІ. Систематизація та узагальнення практичних умінь та навичок
Завдання 3.
Письмово виконай вправи:
-
Розв’язати нерівність
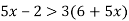
-
Знайти координати вершини параболи
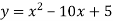 .
.
-
Побудуйте графік функції
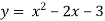 . За графіком знайдіть:
. За графіком знайдіть:
- Область значень функції;
- Проміжок зростання і проміжок спадання функції.
-
В одній системі координат побудувати графіки функцій:
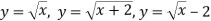 .
.
-
Знайти область визначення функції
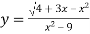 .
.
![]()
1


про публікацію авторської розробки
Додати розробку