Навчальний посібник "Алгебра 9 клас ІІ семестр"

Про матеріал

Посібник розроблений згідно Комбінованої системи М.П. Гузика і може бути використаний як додатковий матеріал для учнів на уроки. Кожна тема посібника має таку структуру: - перший урок – урок розбору блоку навчальної інформації; - наступні уроки – уроки фронтального опрацювання матеріалу, - між уроками фронтального опрацювання містяться завдання по підготовці до уроків індивідуального опрацювання матеріалу; - в кінці кожної теми є один урок внутрішньопредметного узагальнення матеріалу, на якому кожен продемонструє свої знання блоку, а також узагальнить знання і вміння, здобуті під час теми.

Перегляд файлу

Блок №4. Квадратна нерівність. Системи рівнянь другого степеня з двома змінними

Урок №1

Квадратна нерівність. Системи рівнянь другого степеня з двома змінними

«Маленькі рішення, які ми приймаємо

кожного дня, мають величезне значення»

Клайв Стейплз Льюїс, англійський письменник

Питання

Квадратна нерівність. Розв’язування квадратних нерівностей.
Розв’язування систем рівнянь другого степеня з двома змінними.
Розв’язування текстових задач за допомогою систем рівнянь.

Література

Істер О.С. Алгебра: Підручник для 9 класу, §12 – 14, стор. 111 – 148.

1. Квадратна нерівність. Розв’язування квадратних нерівностей.
1.1	Нерівності виду , де x – змінна, a, b, c – деякі числа, , називають квадратними.
1.2	Схема розв’язування квадратних нерівностей: знайти корені квадратного рівняння ; якщо нерівність має строгий знак (), то корені квадратного рівняння позначаємо на осі «виколотими» точками (вони виключаються з множини розв’язків нерівності; Якщо знак нерівності нестрогий (), то коренів рівняння позначаємо зафарбованими точками (вони включатимуться до множини розв’язків нерівності); побудувати ескіз графіка квадратичної функції, включаючи напрям віток параболи; записати проміжки осі Ох, для яких точки параболи розміщені вище від осі Ох (для випадків , ) і нижче від осі Ох (для випадків , ).	; – вітки вгору; ; За теоремою Вієта: . Відповідь: .
2. Розв’язування систем рівнянь другого степеня з двома змінними.
2.3	Якщо необхідно знайти спільні розв’язки двох (і більше) рівнянь з двома змінними, то кажуть, що треба розв’язати систему рівнянь з двома змінними.
2.4	Розв’язком системи рівнянь з двома змінними називається впорядкована пара значень змінних, що задовольняють одразу всі рівняння системи.
2.5	Розв’язати систему рівнянь означає знайти всі її розв’язки або довести, що їх немає.
2.6	Якщо система не має розв’язків, то її називають несумісною.
2.7	Основні способи розв’язування систем рівнянь з двома змінними: 1) графічний; 2) спосіб підстановки; 3) спосіб алгебраїчного додавання; 4) спосіб заміни змінних.
3. Розв’язування текстових задач за допомогою систем рівнянь.
3.8	Схема розв’язування задач за допомогою систем рівнянь з двома змінними: 1)позначити деякі дві невідомі величини буквами (наприклад, ); 2) за умовою задачі скласти систему рівнянь; 3) розв’язати одержану систему; 4) адаптувати здобуті розв’язки відповідно до умови задачі; 5) записати відповідь.

Уроки №2, 3

«Як скаже хто «Я Бога люблю», та

ненавидить брата свого, той неправдомовець»

1 Івана 4:20

Фронтальне опрацювання матеріалу

Квадратна нерівність. Розв’язування квадратних нерівностей

І. Робота над засвоєнням понять, термінів і правил

Завдання 1.

Повтори тези 1.1 – 1.2 блоку № 4.
Усно дай відповіді на питання:

Яка нерівність називається квадратною? Наведіть власний приклад.
Розкажи, за якою схемою розв’язуються квадратні нерівності.
1. Самостійно розглянь приклад розв’язування квадратної нерівності.

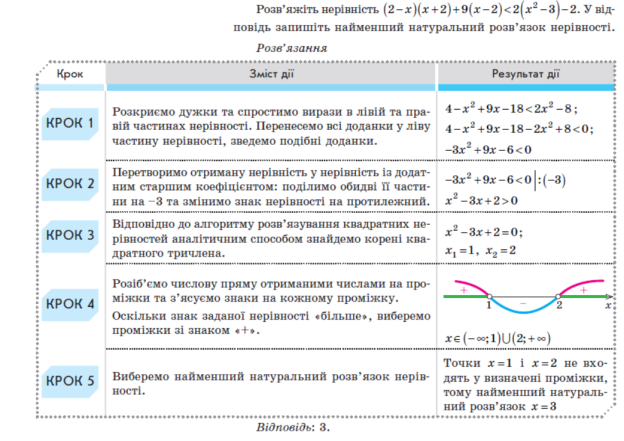
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ

Завдання 2.

Письмово виконай вправи, стор. 115 – 116 підручника:

477, 481 (1, 4), 489, 493, 498.

Завдання 3.

Задача «Планування виробництва». Компанія щомісяця виготовляє одиниць сільськогосподарської продукції. Залежність доходу (у тис. грн) компанії за місяць від можна змоделювати функцією де . Визначте, якими мають бути значення , щоб дохід перевищував 15 млн грн.

Завдання 4.

ЗАДАЧА «МОДЕЛІ ПРОГНОЗУВАННЯ»

Керівництву компанії, що займається продажем складного обладнання, для прогнозування прибутків запропоновано дві математичні моделі, засновані на різних методах маркетингу.

Модель А має вигляд , модель В має вигляд де — кількість (у сотнях) проданих одиниць продукції, — прогнозований

прибуток (у тис. грн).

Для яких значень за моделлю В прогнозується більший прибуток, ніж за моделлю А?

$C:\Users\секретар\Desktop\3b2435b942b6943beaaf-1.jpg$ Готуємось до індивідуального опрацювання матеріалу

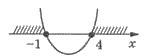
Розв’язати нерівність .
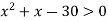Знайти область визначення функції .
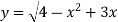Розв’язати нерівність .
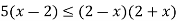Каскадер стрибає у воду з висоти 45 м. Його висота над водою (у м) змінюється за законом 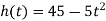, де 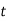– час (у с), що прийшов з моменту стрибка ().

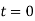Визначте, через скільки секунд після стрибка каскадер опиниться у воді.
Укажіть проміжок часу (у с), протягом якого каскадер залишиться на висоті, більшій за 25 м.

Уроки №5, 6

«Ми отримуємо від життя те, у що віримо…»

Газетна публікація

Фронтальне опрацювання матеріалу

Розв’язування систем рівнянь другого степеня з двома змінними

І. Робота над засвоєнням понять, термінів і правил

Завдання 1.

Повтори тези 2.3 – 2.7 блоку № 4.
Усно дай відповіді на запитання:

Коли кажуть, що потрібно розв’язати систему рівнянь з двома змінними?
Що є розв’язком системи рівнянь з двома змінними?
Що означає розв’язати систему рівнянь з двома змінними?
Яка система рівнянь називається несумісною?
Які є основні способи розв’язування систем рівнянь другого степеня з двома змінними?

ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ

Завдання 2.

Виконайте усно вправу 523 ст. 126 з підручника.

Завдання 3.

Письмово виконай вправи, стор. 126 – 127 підручника: 527 (1, 2);529; 533.

Завдання 4.

Письмово виконай вправи, стор. 128 підручника: 540 (1), 541 (1, 2).

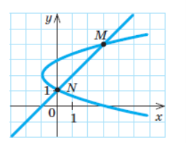
ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач і вправ

Завдання 6.

ЗАДАЧА «ТУРИСТСЬКІ МАРШРУТИ»

На рис. 9 зображено схеми двох туристських маршрутів у прямокутній системі координат. Маршрути описуються рівняннями і . Маршрут А має вигляд параболи, а маршрут В — прямої. У точках M і N перетину цих маршрутів заплановано відпочинок.

1 Визначте координати точок M і N.

2 Який маршрут проходить через населений пункт, розташований в точці (0;3)?

3 Дві групи туристів, що рухаються за маршрутами A і B, зустрілися в точці N на відпочинку, а потім одночасно вирушили в напрямку точки M. За яким маршрутом рухається група, яка прийде в точку M раніше, якщо швидкості руху обох груп однакові? Відповідь поясніть.

Уроки №7, 8

«Розв’язуючи одну задачу різними способами,

можна за допомогою порівнянь з’ясувати, який з них

коротший і ефективніший. Так виробляється досвід»

Уолт Сойєр, австралійський математик

Фронтальне опрацювання матеріалу

Розв’язування текстових задач за допомогою систем рівнянь

І. Робота над засвоєнням понять, термінів і правил

Завдання 1.

Повтори тези 2.3 – 3.8 блоку № 4.
Усно дай відповідь на питання:

Коли кажуть, що потрібно розв’язати систему рівнянь?
Що називають розв’язком системи рівнянь?
Що означає розв’язати систему рівнянь?
Яка система рівнянь називається несумісною?
Які є основні способи розв’язування систем рівнянь?
Як розв’язати задачу за допомогою системи рівнянь з двома змінними?

Завдання 2.

Розглянь приклади розв’язування задач за допомогою систем рівнянь, запропоновані вчителем.

ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ

Користуючись розглянутими прикладами, виконай вправи:

Завдання 3.

Письмово виконай вправи, стор. 133 – 134 підручника: 555, 561, 562.

Завдання 4.

Письмово виконай вправи, стор. 134 – 135 підручника: 568, 570, 573.

ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач і вправ

Завдання 5.

5.1. Протягом вихідних днів до інтернетмагазину надійшло 72 замовлення. Менеджери Андрій і Максим упродовж понеділка мають їх опрацювати. Відомо, що за той самий час Андрій опрацьовує 6 замовлень, а Максим — 5 замовлень. Скільки замовлень опрацьовує

за 1 год кожний менеджер, якщо всі замовлення Андрій може опрацювати на 1,5 год швидше, ніж Максим?

5.2. Відстань між ролердромом і тенісним кортом 700 м. Зоя вирушила з корту до ролердрому, а через 3 хв після цього з ролердрому до корту пішов Юрій, який зустрівся із Зоєю через 3 хв після свого виходу. Відстань між ролердромом і кортом Зоя долає на 2,1 хв швидше, ніж Юрій. Знайдіть швидкість Зої.

$C:\Users\секретар\Desktop\3b2435b942b6943beaaf-1.jpg$ Готуємось до індивідуального опрацювання матеріалу

Графічно розв’яжи систему рівнянь
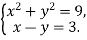
Розв’яжи систему рівнянь способом підстановки
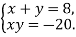
Розв’яжи систему рівнянь способом додавання
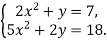
З пунктів А і В, відстань між якими 9 км, вийшли одночасно назустріч один одному два туристи і зустрілись через 1 год. Турист, який вийшов з пункту А, прибув у пункт В на 27 хв пізніше, ніж інший турист, який прибув у пункт А. Знайди швидкість кожного туриста.

Урок №10

«Математику неможливо вивчати,

спостерігаючи, як це робить сусід!»

Айвен Нівен, американський математик

Внутрішньопредметне узагальнення матеріалу

Квадратна нерівність. Системи рівнянь другого степеня з двома змінними

І. Систематизація та узагальнення теоретичних знань

Завдання 1.

Повтори блок № 4. Особливу увагу зверни на тези: 1.1; 1.5; 1.6; 1.7; 1.8; 2.10; 2.11; 2.12; 2.13; 4.15; 4.16; 4.17.
Дай письмово відповідь на питання, запропоновані вчителем.

Завдання 2.

Усно виконай вправи:

Яка з наведених нерівностей рівносильна нерівності ?

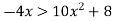А	Б	В	Г

Яка пара чисел є розв’язком системи рівнянь ?

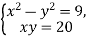А	Б	В	Г

Квадрат числа х на 5 більший за добуток чисел х і у. Знайди ці числа, якщо число х на 2 більше за число у. Яка із систем відповідає цій умові?

А	Б	В	Г

ІІ. Систематизація та узагальнення практичних умінь та навичок

Завдання 3.

Письмово виконай вправи:

Розв’яжи нерівність: 1) 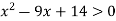; 2) .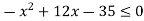
Розв’яжи систему рівнянь
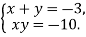
Знайди область визначення функції .
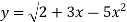Знайди сторони прямокутника, периметр якого дорівнює 92 см, а довжина діагоналі дорівнює 34 см.
Розв’яжи систему рівнянь

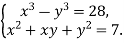
Домашнє завдання: За допомогою сервісу Desmos, намалюйте «веселе обличчя», використовуючи підказки на рисунку. Намалюйте свій малюнок на будь-яку тематику.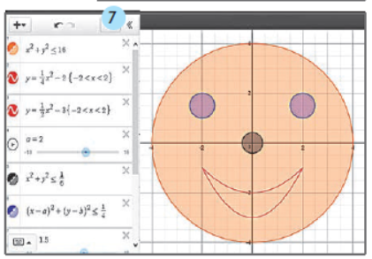

Блок №5. Числові послідовності

Урок №1

Числові послідовності

«Алгебра і геометрія – єдині

країни, де панують тиша й мир»

Марія Аньєзі, італійський математик і філософ

Питання

Числові послідовності.
Арифметична прогресія.
Геометрична прогресія.

Література

Істер О.С. Алгебра: Підручник для 9 класу, §15 – 18, §20, стор. 149 – 177, 181 – 194.

1. Числові послідовності
1.1	Об’єкти, які пронумеровано поспіль натуральними числами 1, 2, 3, …, n утворюють послідовності.	1) 2; 4; 6; 8; … 2) 0; 1; 2; 3; …; 9 Позначення – послідовність; - члени послідовності
1.2	Якщо послідовність утворена числами, то вона називається числовою.
1.3	Числа, які утворюють послідовність називаються членами послідовності.
1.4	Послідовність вважають заданою, якщо кожен її член можна визначити за його номером.
1.5	Способи задання послідовностей 1) перелік усіх членів; 2) описом; 3) формулою n – го члена; 4) рекурентною формулою (формула показує, як виражається наступний член через попередній)	1) 5; 10; 20; 40; …; 2) послідовність парних чисел; 3) ; 4)
1.6	Види числових послідовностей: 1) скінченні та нескінченні; 2) зростаючі та спадні
2. Арифметична прогресія
2.7	Арифметичною прогресією називають послідовність, кожний член якої, починаючи із другого, дорівнює попередньому члену, до якого додано одне й те саме число d. d - різниця арифметичної прогресії	2; 4; 6; 8; 10: d = = 4 – 2 = 2
2.8	Будь – який член арифметичної прогресії, крім першого, дорівнює середньому арифметичному двох сусідніх з ним членів.
2.9	Формули: - формула n – го члена – формула суми n перших членів арифметичної прогресії.
3. Геометрична прогресія
3.10	Геометричною прогресією називають послідовність із відмінним від 0 першим членом, кожний член якої, починаючи з другого, дорівнює попередньому члену, помноженому на одне й те саме відмінне від 0 число q. q – знаменник геометричної прогресії.	2; 4; 8; 16; …
3.11	Квадрат будь – якого члена геометричної прогресії, крім першого) дорівнює добутку двох сусідніх із ним членів
3.12	Формули n – го члена; - формула суми n перших членів геометричної прогресії.

Урок №2

«Мудрі славу вспадковують,

а нерозумні носитимуть сором»

Книга приповістей Соломонових 3:35

Фронтальне опрацювання матеріалу

Числові послідовності

І. Робота над засвоєнням понять, термінів і правил

Завдання 1.

Повтори тези 1.1 – 1.6 блоку № 5.
Усно дай відповіді на питання:

Що таке послідовність? Наведи приклад.
Яка послідовність називається числовою?
Що називають членами послідовності?
Яка послідовність вважається заданою?
Назви способи задання послідовностей.
Які є види числових послідовностей?

ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ

Завдання 2.

Письмово виконай вправи, стор. 152 – 154 підручника: 671, 673, 676, 678 (1, 3).

Завдання 3.

ЗАДАЧА «ТРЕЙЛЕР ДО НОВОГО ФІЛЬМУ»

Напередодні виходу кінофільму на екрани був випущений трейлер до цього фільму. На другий день після виходу трейлера його переглянула половина всіх учнів школи. Частину учнів школи, що переглянули трейлер на n-й день після його виходу, можна визначити за формулою .

1 Яка частина учнів школи переглянула трейлер на третій день після його виходу?

2 Скільки відсотків усіх учнів школи переглянули трейлер на четвертий день після його виходу?

3 Скільки відсотків усіх учнів школи ще не переглянули трейлер на п’ятий день після його виходу?

4 Запишіть формулу (послідовність ), за якою можна знайти частину учнів школи, які не переглянули трейлер на n-й день після його виходу.

5 Знайдіть n — найменший номер дня прокату трейлера, коли його переглянули не менше ніж 90% усіх учнів школи.

Урок №3

«бо Господь дає мудрість,

з Його уст – знання й розум! »

Книга приповістей Соломонових 2:6

Фронтальне опрацювання матеріалу

Арифметична прогресія, її властивості. Формула n-го члена арифметичної прогресії

І. Робота над засвоєнням понять, термінів і правил

Завдання 1.

Повтори тези 1.1 – 2.9 блоку № 5.
Усно дай відповіді на питання:

Що таке послідовність?
Яка послідовність називається числовою?
Назви способи задання послідовностей.
Що називають арифметичною прогресією?
Яку властивість має будь-який член арифметичної прогресії?
Запиши формулу n-го члена арифметичної прогресії.

Завдання 2.

Усно виконай вправу 690 стор. 159 підручника.

ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ

Завдання 3.

Письмово виконай вправи, стор. 160 підручника: 694, 699, 706, 708, 714.

ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач і вправ

Завдання 4.

У магазині «Fruttis» яблука викладено в чотирикутну піраміду (див. рисунок). Сторона першого (нижнього) шару складається з 12 яблук, сторона кожного наступного шару містить на одне яблуко менше, ніж сторона попереднього. Скільки яблук містить сторона шостого шару піраміди?

Урок №4

«бо Господь дає мудрість,

з Його уст – знання й розум! »

Книга приповістей Соломонових 2:6

Фронтальне опрацювання матеріалу

Формула суми перших n членів арифметичної прогресії

І. Робота над засвоєнням понять, термінів і правил

Завдання 1.

Повтори тези 1.1 – 2.9 блоку № 5.
Усно дай відповіді на питання:

Що таке послідовність?
Яка послідовність називається числовою?
Назви способи задання послідовностей.
Що називають арифметичною прогресією?
Яку властивість має будь-який член арифметичної прогресії?
Запиши формулу n-го члена арифметичної прогресії.
Запиши формулу суми перших n членів арифметичної прогресії.

ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ

Завдання 2.

Письмово виконай вправи, стор. 166 підручника: 730, 733, 734.

Завдання 3.

Письмово виконай вправи, стор. 167 підручника: 742, 744, 746.

ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач і вправ

Завдання 4.

2014 р. в місті відкрили 2 точки безкоштовного доступу до Wi-Fi. Кожного наступного року відкривали на 3 таких точки більше, ніж попереднього. Скільки всього таких точок доступу до Wi-Fi відкрили в місті за 3 роки (2014–2016)?

Домашнє завдання: для кращої підготовки до ІОМ, за бажанням, можете пройти тестування за посиланням https://goo.gl/QDMZ7m.

$C:\Users\секретар\Desktop\3b2435b942b6943beaaf-1.jpg$ Готуємось до індивідуального опрацювання матеріалу

Знайди чотири перші члени послідовності 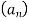, якщо .
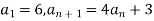Запиши формулу n-го члена арифметичної прогресії 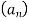та знайди 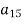, якщо .
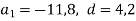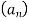– арифметична прогресія. Знайди .
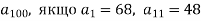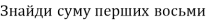членів арифметичної прогресії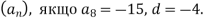
Знайди перший член і різницю арифметичної прогресії, якщо сума трьох перших її членів дорівнює 3, а сума чотирьох перших членів дорівнює 16.

Урок №6

«Хто зневажає досягнення математики, той

завдає шкоди всій науці, бо той, хто не знає математики,

не може вивчати інші точні науки й не може пізнати світ»

Роджер Бекон, англійський філософ

Фронтальне опрацювання матеріалу

Геометрична прогресія, її властивості. Формула n-го члена геометричної прогресії

І. Робота над засвоєнням понять, термінів і правил

Завдання 1.

Повтори тези 3.10 – 3.12 блоку № 5.
Усно дай відповіді на питання:

Що називають геометричною прогресією?
Яку властивість має будь-який член геометричної прогресії, крім першого?
Запиши формулу n-го члена геометричної прогресії.

Завдання 2.

Встанови відповідність між формулою та її назвою


Означення арифметичної прогресії
Означення геометричної прогресії
Формула n-ого члена арифметичної прогресії
Формула n-ого члена геометричної прогресії
Різниця арифметичної прогресії
Знаменник геометричної прогресії
Сума n перших членів арифметичної прогресії
Сума n перших членів геометричної прогресії
Властивість членів арифметичної прогресії
Властивість членів геометричної прогресії

ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ

Завдання 3.

Письмово виконай вправи, стор. 174 підручника: 765 (1, 3), 770 (2, 4), 774, 779 (1, 3), 781.

ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач і вправ

Завдання 4.

Самостійне завдання

1. в₁=2,4; в₂=24. Знайти: q.

2. в₁=4, q =½. Знайти: в₂.

3. в₁= -2,5; q =2. Знайти: в₅.

4. в₁= 3; q = -2; в_n= 3072. Знайти: n.

5. в₄= -432; q =2; Знайти:в₁.

6. в_n=; Знайти: в₁

7. Між числами 40 і 2,5 вставити таке число, яке разом з даними утворило б геометричну прогресію.

Відповіді записати в таблицю і відгадати зашифроване слово

1	2	3	4	5	6	7

Шифр:

10	-20	-0,06	320	-54	2	5	11	12	28	-40
А	Ю	Р	Я	Б	Л	О	Е	В	М	Г

Урок №7

«Хто зневажає досягнення математики, той

завдає шкоди всій науці, бо той, хто не знає математики,

не може вивчати інші точні науки й не може пізнати світ»

Роджер Бекон, англійський філософ

Фронтальне опрацювання матеріалу

Сума n перших членів геометричної прогресії

І. Робота над засвоєнням понять, термінів і правил

Завдання 1.

Повтори тези 3.10 – 3.12 блоку № 5.
Усно дай відповіді на питання:

Що називають геометричною прогресією?
Яку властивість має будь-який член геометричної прогресії, крім першого?
Запиши формулу n-го члена геометричної прогресії.
Запиши формулу суми n перших членів геометричної прогресії.

ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ

Завдання 2.

Письмово виконай вправи, стор. 184 підручника: 812 (1, 3), 822, 825.

Завдання 3.

$C:\Users\нна\Desktop\561b9fe10a3d76fd5a1609dcec276af2_r_1.jpg$ Селянин продавав 20 овець за 200 грн. Коли один із покупців став надто довго торгуватися, селянин запропонував : „Дай за першу вівцю 1 к., за другу – 2 к., за третю – 4 к., за кожну наступну – вдвічі більше копійок, ніж за попередню.” Покупець погодився. Скільки він заплатив за тих 20 овець?

Організатори проведення флешмобу до Дня матері в Україні вирішили використати для зв’язку між учасниками смс-повідомлення. Один з учасників отримав повідомлення з проханням надіслати відповідну інформацію чотирьом іншим, які,y свою чергу, надіслали смс-повідомлення ще чотирьом учасникам і т.д. Скільки yчасників флешмобу отримають інформацію протягом 20 хв, якщо один учасник виконує це доручення за 2 хв? Усі надіслані повідомлення вважайте отриманими.
ЗАДАЧА «СТРИБКИ З ПАРАШУТОМ» Парашутисти стрибають із літака і в повітрі утворюють кола, тримаючи одне одного за руки. Перше коло складається із 3 парашутистів. Кожне наступне коло складається з удвічі більшої кількості парашутистів, ніж попереднє.

Визначте кількість парашутистів, з яких складається третє коло.
Складіть формулу, за якою можна обчислити кількість x_n парашутистів, що утворюють n-не коло.
Скільки парашутистів перебувають у повітрі, якщо всього утворилося 5 кіл?

Урок №8

«Приклади в навчанні корисніші за правила»

Ісаак Ньютон

Фронтальне опрацювання матеріалу

Розв’язування практичних задач на прогресії

І. Робота над засвоєнням понять, термінів і правил

Завдання 1.

Повтори тези 3.10 – 3.12 блоку № 5.
Усно дай відповіді на питання:

Що називають геометричною прогресією?
Яку властивість має будь-який член геометричної прогресії, крім першого?
Запиши формулу n-го члена геометричної прогресії.
Запиши формулу суми n перших членів геометричної прогресії.

ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ

папирус райнда Завдання 2.

$C:\Users\нна\Desktop\Без названия (2).jpg$ 2.1. Є 7 будинків, в кожному будинку по 7 котів, кожен кіт з’їдає 7 мишей, кожна миша з’їдає по 7 колосків ячменю, кожен колосок, якщо посіяти зерно з нього, дає 7 мір ячменю. Знайти суму загальної кількості будинків, котів, мишей, колосків і мір.

2.2. Мешканець маленького містечка був відомий своєю скнарістю. Коли в нього були справи в повітовому місті, розташованому на відстані 25 км від цього містечка, він, зазвичай, шукав сусідів, які б підвезли його. Одного разу скнара крутився на площі, шукаючи того, хто підвіз би його «за спасибі» додому. Але цього разу нікого не було, і він змушений був шукати платного візника. Скнара обійшов їх усіх, торгуючись з ними й порівнюючи ціни. Один просив 250 крб., другий — 200 крб., а третій — 150 крб. Усі ці ціни здалися йому занадто високими. Нарешті він помітив візника з убогим візком і жалюгідною шкапою. Коли скнара запитав його, скільки він візьме за дорогу, той подивився на землю, почухав потилицю і відповів: «За перший кілометр заплатите мені 1 коп., за другий — 2 коп., за третій — 4 коп., за четвертий — 8 коп., і так до кінця шляху». «От чудний, — подумав скнара, ледве стримуючи сміх, — лічить на копійки». Поспіхом він заліз у візок і гукнув «Згоден! Поїхали !» Скільки карбованців він повинен заплатити за дорогу ?

2.3. Три числа утворюють арифметичну прогресію. Якщо до першого числа додати 8, то дістанемо геометричну прогресію, для якої . Знайдіть ці числа.

2.4. Зареєструвавшись у соціальній мережі Facebook, першого дня Микита додав у друзі 32 особи. Кожного наступного дня кількість друзів Микити збільшувалась втричі порівняно з попереднім днем.

1) Скільки друзів з’явилось у Микити в цій соціальній мережі за третій день з моменту реєстрації?

2) Скільки всього друзів з’явилось в Микити в цій соціальній мережі за перші три дні з моменту реєстрації?

2.5. Цікаво, яким буде ваш вибір?..

Уявіть собі, що ви опинились перед вибором: або отримати 100 000 доларів прямо зараз, або протягом 28 днів отримувати гроші, починаючи з одного цента, при умові, що кожного наступного дня ця сума буде подвоюватись?

2.6. Перша частина культової трилогії «Володар перснів» забрала у світовому прокаті 123 млн. доларів. Кожна наступна збирала суму (у млн. дол.) утричі більшу, ніж попередня.

1) Яку суму зібрала у світовому прокаті третя частина трилогії?

2) Яку загальну суму зібрала у світовому прокаті культова трилогія?

Урок №9

«Приклади в навчанні корисніші за правила»

Ісаак Ньютон

Фронтальне опрацювання матеріалу

Геометрична прогресія

І. Робота над засвоєнням понять, термінів і правил

Завдання 1.

Повтори тези 3.10 – 3.12 блоку № 5.
Усно дай відповіді на питання:

Що називають геометричною прогресією?
Яку властивість має будь-який член геометричної прогресії, крім першого?
Запиши формулу n-го члена геометричної прогресії.
Запиши формулу суми n перших членів геометричної прогресії.

ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ

Завдання 2.

Усно виконай вправи:

Яка з наведених послідовностей є геометричною прогресією?

А	Б	В	Г
3; 9; 27; 81	40; 20; 10; 2	4; 8; 32; 64	2; – 10; 50; 250

Знайди знаменник геометричної прогресії 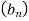, якщо , .

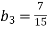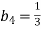А	Б	В	Г

Знайди четвертий член геометричної прогресії 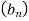, якщо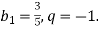

А	Б	В	Г

Завдання 3.

Письмово виконай вправи:

У геометричній прогресії 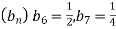. Знайди .
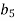Знайди суму чотирьох перших членів геометричної прогресії 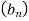, якщо .
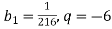Восьмий член геометричної прогресії дорівнює 9, а знаменник 3. Знайди її десятий член.
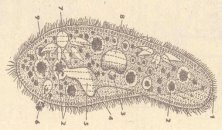Знайдіть знаменний геометричної прогресії 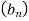, якщо .
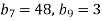Розв’яжи задачу, використовуючи формули геометричної прогресії: «Інфузорія туфелька розмножується поділом на 2 частини. Скільки інфузорій було спочатку, якщо після 8-го поділу їх стало 320?»

$C:\Users\секретар\Desktop\3b2435b942b6943beaaf-1.jpg$ Готуємось до індивідуального опрацювання матеріалу

У геометричній прогресії 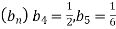. Знайди .
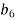Знайди суму чотирьох перших членів геометричної прогресії 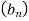, якщо .
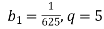Шостий член геометричної прогресії дорівнює 16, а знаменник 2. Знайди її дев'ятий член.
Знайди знаменник геометричної прогресії, якщо .

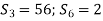Урок №11

«Математику неможливо вивчати,

спостерігаючи, як це робить сусід!»

Айвен Нівен, американський математик

Внутрішньопредметне узагальнення матеріалу

Числові послідовності

І. Систематизація та узагальнення теоретичних знань

Завдання 1.

Повтори блок № 5. Особливу увагу зверни на тези: 2.7 – 3.12.
Дай письмово відповідь на питання, запропоновані вчителем.

ІІ. Систематизація та узагальнення практичних умінь та навичок

Завдання 2.

Усно виконай вправи:

Яка з наведених послідовностей є арифметичною прогресією?

А	Б	В	Г

Яка з наведених послідовностей є геометричною прогресією?

А	Б	В	Г
	14; 28; 42; 54; …

Дано арифметичну прогресію 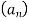. Знайдіть 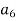, якщо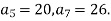

А	Б	В	Г
1	40	20	23

Завдання 3.

Письмово виконай вправи:

Знайди 10-й член арифметичної прогресії 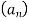, якщо .
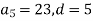Знайди суму перших шести членів арифметичної прогресії 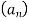, якщо .
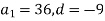Знайди суму перших п'яти членів геометричної прогресії 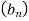, якщо , .
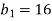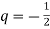Між числами 64 і 27 розмісти два числа, які б разом із даними утворювали геометричну прогресію.
Перший і четвертий члени арифметичної прогресії відповідно дорівнюють 6 і 9. Знайди суму її перших восьми членів.
Послідовність 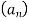– арифметична прогресія, 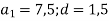. Чи є членом цієї прогресії число 31?
Знайдіть чотири перші члени геометричної прогресії, в якій різниця між другим і першим членами дорівнює 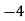, а різниця між третім і першим членами дорівнює 8.

Блок №6. Основи комбінаторики, теорії ймовірностей та статистики

Урок №1

Основи комбінаторики, теорії ймовірностей та статистики

«…математика безмежно різноманітна,

як світ, і присутня, міститься в усьому»

М.П. Єругін, білоруський математик

Питання

Відсоткові розрахунки.
Комбінаторні задачі. Комбінаторні правила суми і добутку.
Випадкова подія. Частота і ймовірність випадкової події.
Початкові відомості про статистику.

Література

Істер О.С. Алгебра: Підручник для 9 класу, §19, §21 – 24, стор. 178 – 181, 195 – 234.

1. Відсоткові розрахунки
1.1	Відсотком (процентом) називається сота частина цілого (яке береться за одиницю).	1% = 0,01 128% = 1,28 58% = 0,58
1.2	Щоб знайти відсотки від числа, потрібно ці відсотки перетворити у дріб і дане число помножити на цей дріб.	Знати 7% від числа 300. 7% = 0,07; 0, 07∙300 = 21
1.3	Щоб знайти число за заданим значенням його відсотків, потрібно ці відсотки перетворити у дріб і дане число поділити на цей дріб.	Знайти число, 30% якого дорівнює 24. 30% = 0,3; 2) 24 : 0,3 = 80.
1.4	Щоб знайти скільки відсотків число a становить від числа b, потрібно a поділити на b і помножити на 100 %.	Скільки відсотків становить число 26 від числа 65? (26 : 65) ∙ 100 = 40%
1.5	Якщо задане число щороку (щомісяця, щодня тощо) збільшується (зменшується) на р%, то в цьому випадку говорять про складні відсотки.
1.6	Формула складних відсотків – збільшення – зменшення
2. Комбінаторні задачі. Комбінаторні правила суми і добутку
2.7	Комбінаторика – розділ математики, що вивчає питання вибору та розташування елементів деякої скінченної множини відповідно до певних умов.		Скількома способами легкоатлет може вибрати собі пару взуття, маючи 5 пар кросівок і 2 пари кедів?
2.8	Комбінаторне правило суми: Якщо деякий елемент можна вибрати способами, а деякий елемент (незалежно від вибору елемента ) – способами, то вибрати АБО можна способами.		способів – вибрати пару взуття
2.9	Комбінаторне правило добутку: Якщо деякий елемент можна вибрати способами, а деякий елемент (незалежно від вибору елемента ) – способами, то вибрати І можна способами.		У меню шкільної їдальні є на вибір 4 види пиріжків і 3 види соку. Скільки різних варіантів вибору 1 пиріжка і 1 соку є в учня цієї школи? способів
3. Випадкова подія. Частота і ймовірність випадкової події
3.10	Результат спостереження, досліду, експерименту називають подією
3.11	Класифікація подій: 1) вірогідні (достовірні) – події, які обов’язково відбудуться за певних умов; 2) неможливі – події, які не відбудуться за жодних умов; 3) випадкові – події, які можуть відбутися або не відбутися за певних умов
3.12	Якщо за незмінних умов проведено випадкових дослідів і в випадків подія відбулася, то число називається частотою події .
3.13	Ймовірність випадкової події А дорівнює відношенню кількості випадків, які сприяють події А, до кількості всіх можливих випадків.
4. Початкові відомості про статистику
4.14	Статистика – це наука про отримання, оброблення й аналіз кількісних даних, які характеризують масові явища.
4.15	Етапи статистичного дослідження: 1) збирання даних; 2) оброблення даних та їх подання у зручній формі; 3) аналіз даних; 4) висновки й рекомендації.
4.16	Вибіркою називається сукупність об’єктів, на основі яких проводять дослідження.
4.17	Частотами – це числа, які показують як часто трапляються у вибірці ті чи інші значення.
4.18	Дані статистичних досліджень зручно подавати у вигляді стовпчастих діаграм (гістограм), кругових діаграм та графіків.
4.19	Середнім значенням статистичних вимірювань називають середнє арифметичне статистичних даних.

Урок №2

«Велика душа, як великий вогонь, видна здалеку…»

Народна мудрість

Фронтальне опрацювання матеріалу

Відсоткові розрахунки. Формула складних відсотків

І. Робота над засвоєнням понять, термінів і правил

Завдання 1.

Повтори тези 1.1 – 1.6 блоку № 6.
Дай відповіді на питання:

Що таке відсоток?
Як знайти відсоток від числа?
Як обчислити скільки відсотків число а становить від числа b?
Як знайти число за заданим значенням його відсотків?
Запиши на дошці формулу складних відсотків.

ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ

Завдання 2.

Усно виконай вправи:

Яке з наведених рівнянь може бути математичною моделлю реальної ситуації: «Турист ішов 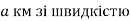5 км / год і 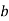км зі швидкістю 4 км / год і на весь шлях витратив 6 год»?

У саду росте 50 дерев. Яблуні становлять 30 %. Скільки яблунь росте у саду?

А	Б	В	Г
45	15	25	16

Скільки відсотків години становлять 12 хв?

А	Б	В	Г
80%	12%	8%	20%

Завдання 3.

Письмово виконай вправи:

У скільки разів збільшиться величина, якщо її збільшити на 50 %?
У двох цехах заводу працює 1240 робітників. З них 55 % працює у першому цеху. Скільки робітників працює у другому цеху?
У сплаві 45 % алюмінію, а решту – 5450 г – магній. Яка маса цього сплаву?
До 400 г 15-відсоткового розчину солі додали ще 100 г води. Визначити у відсотках вміст солі у новому розчині.
Вкладник поклав до банку 5000 гривень на два різні рахунки. За першим з них банк нараховує 10 % річних, а за другим – 8 % річних. Через рік кількість грошей на першому рахунку стала на 1140 грн. більшою, ніж на другому. Скільки гривень було покладено на кожний рахунок?

Урок №3

«Люблять Батьківщину не за те,

що вона велика, а за те, що своя»
Сенека

Фронтальне опрацювання матеріалу

Комбінаторні задачі

І. Робота над засвоєнням понять, термінів і правил

Завдання 1.

Повтори тези 1.1 – 2.9 блоку № 6.
Дай відповіді на питання:

Що називають відсотком?
Як знайти відсотки від числа?
Як знайти число за заданим значенням його відсотків?
Як знайти, скільки відсотків становить одне число від іншого?
Коли говорять про складні відсотки?
Записати формулу складних відсотків.
Сформулювати комбінаторне правило суми та комбінаторне правило добутку.

ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ

Завдання 2.

Виконай самостійно вправи за наведеним прикладом:

Знайди:

30%від числа 66;

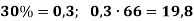
2) 25% від числа 80;

3) 150% від числа 24.

2.2. Знайди:

число, 20% якого дорівнює 36;

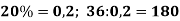
2) число, 40% якого дорівнює 160.

2.3. Знайди, скільки відсотків становить:

число 8 від числа 48;

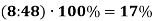
2) число 24 від числа 32.

2.4. Знайди відсоткове відношення величин:

2 кг та 40 кг;

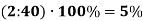
3 грн. та 15 грн.

Завдання 3.

Виконай письмово вправи:

3.1. Вкладник поклав до банку 4000 грн. під 8% річних. Скільки грошей буде на його рахунку через 3 роки?

3.2. Письмово виконати вправи з підручника, стор. 199: 900, 902, 906, 908, 910.

$C:\Users\секретар\Desktop\3b2435b942b6943beaaf-1.jpg$ Готуємось до індивідуального опрацювання матеріалу

У скільки разів збільшиться величина, якщо її збільшити на 100%?
Будівельники проклали 480 м шляхопроводу за два тижні. За перший тиждень вони виконали 45 % роботи. Скільки метрів шляхопроводу проклали будівельники за другий тиждень?
У сплаві 60 % міді, а решта 200 г – олово. Яка маса цього сплаву?
До 400 г 10-відсоткового розчину солі додали ще 80 г солі. Визнач у відсотках вміст солі у новому розчині.
Підприємство поклало до банку 10 700 гривень на два різні рахунки. За першим з них банк виплачує 6 % річних, а за другим – 8 % річних. Через рік кількість грошей на обох вкладах стала однаковою. Скільки гривень було покладено на кожний рахунок?

Урок №5

«Дурень той, хто кидає справу на півдорозі і

дивиться, роззявивши рот, з боку, що з усього цього вийде»
Фрідріх Шиллер, німецький поет

Фронтальне опрацювання матеріалу

Випадкова подія. Ймовірність випадкової події

І. Робота над засвоєнням понять, термінів і правил

Завдання 1.

Повтори тези 1.1 – 3.13 блоку № 6.
Дай відповіді на питання:

Що називають подією?
Які бувають події? Наведіть приклади.
Що називають ймовірністю події?
Що називають частотою події?

ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ

Завдання 3.

Перегляньте відео, запропоноване вчителем.
Письмово виконайте вправи, використовуючи інформацію з відеоролика та блоку.

Беруть навмання пластинку доміно. Яка ймовірність того, що на ній є всього 11 очок?
Уявіть собі, що в класі, в якому ви навчаєтесь, розігрується одна безкоштовна поїздка до Лондона. Яка ймовірність того, що до Лондона поїдеш ти?
Проведемо 20 підкидань монети. Яка ймовірність випадання герба при такому результаті: РРГРРРГРГГРГГРРГРГРГ?
У грі «російська рулетка» у барабан пістолета з 8 можливих вставляються лише один патрон. Барабан розкручують та виконують постріл. Яка ймовірність того, що постріл буде холостим?
Кидаючи одночасно два гральні кубики, яка ймовірність того, що випадуть два однакові числа?
У коробці було 23 карти, пронумеровані від 1 до 23. Із коробки навмання взяли одну карту. Яка ймовірність того, що на ній записане двоцифрове число?

Уроки №6, 7

«Той, хто не знає математики, не може пізнати

ніякої іншої науки і навіть не може зрозуміти свого невігластва»

Роджер Бекон, англійський філософ, учений,

викладач Оксфордського університету

Фронтальне опрацювання матеріалу

Початкові відомості про статистику

І. Робота над засвоєнням понять, термінів і правил

Завдання 1.

Повтори тези 4.14 – 4.19 блоку № 6.
Усно дай відповіді на питання:

Що називають статистикою?
Які етапи статистичного дослідження?
Що називають вибіркою?
Що таке частоти?
Як обчислити середнє значення?
Як зручно подавати дані статистичних досліджень?

Завдання 2.

Ознайомся з історією розвитку статистики (презентація вчителя)

ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ

Завдання 4.

Письмово виконай вправи:

Продавець на ринку, закупивши оптом лимони, продає їх поштучно за такою ціною:

50 г – 60 г – 70 коп.; 60 г – 70 г – 90 коп.; 70 г – 80 г – 1 грн. 10 коп.; 80 г – 90 г – 1 грн. 30 коп.; 90 г – 100 г – 1 грн. 40 коп.; 100 г – 120 г – 1 грн. 50 коп. Склади частотну таблицю даних задачі. Побудуй гістограму.

На заводі протягом семигодинного робочого дня робітник виготовляв: 10, 8, 11, 12, 11, 9, 7 деталей. Знайди середнє значення. Побудуй гістограму.
Група учнів у кількості 20 чоловік підтягувалася на перекладині. Результати підтягування були такі: 12, 14, 9, 10, 10, 12, 11, 8, 9, 7, 10, 10, 13, 15, 10, 9, 14, 10, 11, 13. Знайди моду, медіану. Склади частотну таблицю.
О шостій годині ранку визначено температуру на десяти метеостанціях. Отримані дані відображено у таблиці:

Температура (у градусах)	1	3	4	Х
Кількість метеостанцій	2	3	4	1

Визнач х, якщо середнє арифметичне всіх цих даних дорівнює 3,5°С.

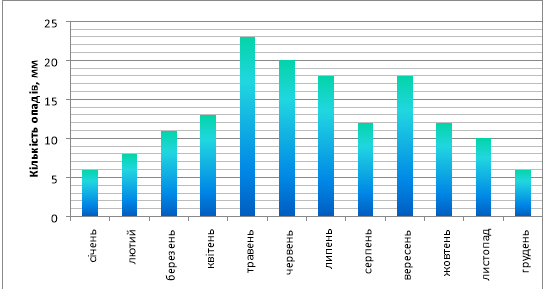
Діаграма, зображена на рисунку, містить інформацію про кількість опадів (у мм), що випали упродовж року в місті N. Користуючись діаграмою, установіть, які з наведених тверджень є правильними.

І. Улітку опадів випало менше, ніж навесні.

ІІ. У вересні опадів випало у 1,5 рази більше, ніж у жовтні.

ІІІ. Середня місячна кількість опадів за рік становить 19 мм.

Завдання 5.

Самостійно виконай вправи (письмово):

Щоб знайти середню масу головки капусти навмання взяли 20 головок, маси яких виявилися: 2,8 кг; 2,8 кг; 2,9 кг; 3,1 кг; 3,2 кг; 3,1 кг; 3,3 кг; 3,2; 3,2 кг; 2,8 кг; 3,5 кг; 3,4 кг; 3,4 кг; 3,2 кг; 2,8 кг; 3,3 кг; 3,6 кг; 3,7 кг; 3,1 кг; 3,6 кг. Знайди середню масу головки. Склади статистичну таблицю.
За результатами тестування 48 студентів склали таблицю кількості допущених помилок.

8	1	2	2	0	3	3	1	3	2	4	2
2	3	0	1	5	3	1	2	4	1	3	2
0	3	2	2	4	3	0	3	3	3	2	3
4	1	0	2	2	1	2	0	1	3	3	2

Склади частотну таблицю і побудуй діаграму.

Результати вимірювання діаметра 200 деталей після шліфування занесені до таблиці:

D, см	6,67-6,69	6,69-6,71	6,71-6,73	6,73-6,75	6,75-6,77	6,77-6,79	6,79-6,81	6,81-6.83
Кількість деталей	5	17	24	54	52	23	18	7

Побудувати полігон частот та гістограму, визначити відносну частоту кожного значення (відносна частота – відношення частоти значення до кількості усіх значень вибірки виражене у відсотках).

$C:\Users\секретар\Desktop\3b2435b942b6943beaaf-1.jpg$ Готуємось до індивідуального опрацювання матеріалу

На полиці стоїть 10 книг, із них дві – з математики. Яка ймовірність того, що навмання взята з полиці книга буде книгою з математики?
Знайди середнє значення вибірки: 7; 11; 13; 3; 7; 2; 7; 3; 32; 37; 5; 9.
У таблиці наведено розміри взуття 20 хлопців 9 класу.

37	37	38	38	38	39	39	39	39	40
40	40	40	40	41	41	42	42	43	43

Склади частотну таблицю розмірів взуття дев’ятикласників.

Побудуй гістограму за даними завдання 6.
У кошику 5 зелених, кілька жовтих та кілька червоних яблук. Скільки жовтих яблук у кошику і скільки червоних, якщо ймовірність витягнути навмання жовте яблуко дорівнює 0,3, а червоне – 0,2?

Урок №9

«Математику неможливо вивчати,

спостерігаючи, як це робить сусід!»

Айвен Нівен, американський математик

Внутрішньопредметне узагальнення матеріалу

Основи комбінаторики, теорії ймовірностей та статистики

І. Систематизація та узагальнення теоретичних знань

Завдання 1.

Повтори блок № 6.
Дай письмово відповідь на питання, запропоновані вчителем.

ІІ. Систематизація та узагальнення практичних умінь та навичок

Завдання 2.

Усно виконай вправи:

На тарілці лежить 5 слив і 7 груш. Скількома способами можна вибрати один фрукт?

А	Б	В	Г
5	6	11	30

Скільки відсотків години становлять 6 хв?

А	Б	В	Г
6%	10%	60%	170%

Виберіть неможливу подію:

А	Б	В	Г
Наступним днем після 1 січня буде 2 січня	Під час підкидання грального кубика випаде 7 очок	При охолодженні до вода перетворюється на лід	Навмання вибране двоцифрове число буде кратне 3

Завдання 3.

Письмово виконай вправи:

Знайдіть середнє значення вибірки 3; 2; 3; 6; 10; 6; 1; 5; 10; 5; 2; 1.
До магазину було завезено 300 кг яблук і груш. 30 % завезених фруктів становили груші. Скільки кілограмів яблук було завезено до магазину?
Маємо два сплави, один з яких містить 20 % міді, а другий – 15 %. Скільки кілограмів кожного з них треба взяти, щоб отримати 90 кг сплаву, який містить 17 % міді?
Вимірявши зріст учнів у класі отримали такі результати (у сантиметрах): 168, 166, 166, 167, 165, 164, 167, 169, 166, 164, 164,164, 165, 169, 162, 164. Подайте ці статистичні дані у вигляді гістограми.
Що вигідніше: покласти у банк 3000 грн. на 2 роки під 11 % річних, чи на 3 роки під 6 % річних?
У скриньці a зелених та b червоних кульок. Яка ймовірність того, що одна навмання взята зі скриньки кулька буде зеленою?
З коробки, що містить х синіх та у жовтих олівців один за одним виймають всі олівці крім одного. Яка ймовірність того, що олівець, який залишився, – синій?

Повторення матеріалу, вивченого за рік

Урок №1

«Алгебра - щедра, вона часто дає більше, ніж у неї просять»

Жан Лерон , французький математик

Внутрішньопредметне узагальнення матеріалу за рік

І . Усно виконати вправи

Обчисліть значення виразу .

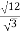А	Б	В	Г
2	4

Якому одночлену дорівнює вираз ?

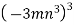А	Б	В	Г

При якому значенні змінної не має змісту вираз ?

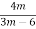А	Б	В	Г
3	2	0	– 3

ІІ. Письмово виконати вправи

Спростіть вираз .
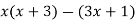Скоротіть дріб .
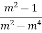Знайдіть перший додатний член арифметичної прогресії
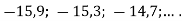
Розв’яжіть рівняння .
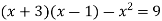Човен пройшов 8 км за течією річки і 6км проти течії, витративши на весь шлях 1 год 12 хв. Швидкість течії становить 3 км ∕ год. Знайдіть швидкість човна за течією.