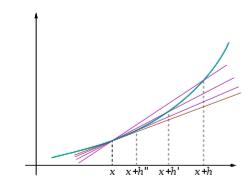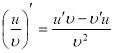Навчальний посібник для учнів "Елементи математики в шкільній фізиці"
|
|
|
ЕЛЕМЕНТИ МАТЕМАТИКИ В ШКІЛЬНІЙ ФІЗИЦІ
|
|
|
|
Зверховська Ніна Георгіївна, вчитель фізики, математики та інформатики загальноосвітньої школи І-ІІІ ступенів №1 м. Ямпіль |
|
|
|
|
|
Ямпіль 2012 |
|
|
 Відділ освіти Ямпільської районної державної адміністрації
Відділ освіти Ямпільської районної державної адміністрації
Районний методичний кабінет



ББК 22я78
З43
Елементи математики в шкільній фізиці. – Ямпіль, 2012р.
Автор: Зверховська Н.Г., вчитель фізики, математики та
інформатики загальноосвітньої школи І-ІІІ ступенів №1
м. Ямпіль
Рецензенти:
Сокирко Н.К. – методист районного методичного кабінету відділу освіти
Ямпільської районної державної адміністрації.
Рочняк Л.Б – вчитель - методист, вчитель фізики та математики
загальноосвітньої школи І-ІІІ ступенів с. Цекинівка
Навчальний посібник „Елементи математики в шкільній фізиці” ставить за мету подолання прогалин в знаннях учнів з математики, які використовуються при вивченні фізики. В основі розробки – власні спостереження та досвід роботи в школі. Матеріал подається так, ніби школярі вперше зустрічаються з даними питаннями, що дає можливість одним – вивчити, іншим – уточнити, повторити або вдосконалити знання з даної теми, а всім - подолати страх та невпевненість у використанні векторних величин та графіків, похідних та інтегралів.
Посібник стане в пригоді учням та вчителям фізики.
Схвалено методичною радою методичного кабінету відділу освіти Ямпільської районної державної адміністрації (протокол №2 від
26 грудня 2012 року).
ЗМІСТ
І.Вступ---------------------------------------------------------------------------------------- 5
1.1.Поради для вчителя---------------------------------------------------------------- 6
1.2.Поради для учня --------------------------------------------------------------------11
1.3.Пам'ятка для учнів------------------------------------------------------------------13
ІІ. Графіки та вектори-------------------------------------------------------------------15
2.1.Графіки---------------------------------------------------------------------------------16
2.2.Графіки в механіці------------------------------------------------------------------18
2.3.Розв'яжи сам------------------------------------------------------------------------- 26
2.4.Графіки в молекулярній фізиці та термодинаміці------------------------29
2.5.Розв'яжи сам-------------------------------------------------------------------------34
2.6.Вектори---------------------------------------------------------------------------------38
2.7.Розв'яжи сам------------------------------------------------------------------------- 48
ІІІ. Похідна та інтеграл -----------------------------------------------------------------49
3.1.З історії---------------------------------------------------------------------------------50
3.2.Похідна---------------------------------------------------------------------------------59
3.3.Розв'яжи сам -------------------------------------------------------------------------74
3.4.Інтеграл--------------------------------------------------------------------------------75
3.5.Розв'яжи сам -------------------------------------------------------------------------79
ІV.. Список використаної літератури-----------------------------------------------81

І.ВСТУП
Створений мною навчальний посібник „Елементи математики в шкільній фізиці.” ставить за мету подолання прогалин в знаннях учнів з тем: графіки, вектори, похідні та інтеграли. В основі розробки – власні спостереження та досвід роботи в школі. Матеріал подається так, ніби школярі вперше зустрічаються з даними питаннями, що дає можливість одним – вивчити, іншим – уточнити, повторити або вдосконалити знання з даної теми, а всім - подолати страх та невпевненість у використанні векторних величин, графіків, похідних та інтегралів.
Найбільші проблеми виникають у школярів при розв’язуванні фізичних задач з даних тем.
Пояснень цьому є багато – це невідповідність програм з фізики та математики, мала кількість навчальних годин, що відводиться на вивчення цих понять на уроках математики, відсутність навичок у використанні вектор, графіків, похідних та інтегралів. Та й складність цих питань для учнів відіграє не останню роль. Та проблема є і її необхідно вирішувати.
Даний посібник містить теоретичний матеріал по використанню графіків та векторів в курсі шкільної фізики та умови задач по їх застосуванню. В ньому зібрані необхідні поняття і правила, які учні вивчають в різних темах при вивченні математики та фізики в різних класах.
Мета даної збірки – ліквідувати прогалини в знаннях, систематизувати знання школярів з даних тем, допомогти на етапі вивчення нового матеріалу.
Навчальний посібник можна використовувати при проведенні факультативних занять з фізики.
- Поради для вчителя
Фізичною задачею називають певну проблему, яка в загальному випадку розв'язується за допомогою логічних умовиводів, математичних дій та експерименту на основі законів фізики.
У методичній літературі під задачами зазвичай розуміють доцільно підібрані вправи, основне призначення яких полягає у вивченні фізичних явищ, формуванні понять, розвитку логічного мислення учнів і прищепленні їм умінь застосовувати свої знання на практиці.
Розв'язування задач є невід'ємною складовою частиною навчального процесу, бо дозволяє формувати і збагачувати фізичні поняття, розвиває фізичне мислення учнів, їх навички застосування знань на практиці. У процесі розв'язування задач формуються працелюбність, допитливість розуму, самостійність у судженнях, виховується інтерес до навчання, загартовується воля і характер, розвивається вміння аналізувати явища, узагальнювати відомості про них тощо. Велика роль задач у здійсненні політехнічного принципу навчання. Розв'язування задач є способом перевірки і систематизації знань, дає можливість раціонально проводити повторення, розширювати і поглиблювати знання, сприяє формуванню світогляду, знайомить з досягненнями науки, техніки т.п.
Усе це дозволяє говорити про розв'язування задач як метод навчання. Вважають, що без розв'язування задач курс фізики не може бути засвоєний.
Фізичні задачі використовуються для:
- створення проблемних ситуацій;
- повідомлення нових знань;
- формування практичних умінь і навичок;
- перевірки глибини і міцності засвоєння знань; повторення і закріплення матеріалу;
- розвитку творчих здібностей учнів та ін.
Розв'язування задач є складовою частиною майже кожного уроку. На комбінованих уроках їх використовують двічі: при опитуванні учнів та при закріпленні вивченого матеріалу.
Для організації повторення підбирають комбіновані задачі. Задачі є ефективним засобом контролю знань учнів.
Задачі відрізняються одна від одної за багатьма ознаками: за змістом, за способом завдання, за дидактичною метою та ін. Класифікація задач за певними ознаками дозволяє раціонально здійснювати їх підбір та розробити методику їх розв'язування. Існують різні класифікації задач. Нижче наведена одна з можливих класифікацій.
КЛАСИФІКАЦІЯ ЗАДАЧ
За змістом: конкретні, абстрактні, з міжпредметним змістом, технічні, історичні, з певних розділів курсу фізики.
За дидактичною метою: тренувальні, творчі, дослідницькі, контрольні.
За способом подання умови: текстові, графічні, експериментальні, задачі-малюнки (або фотографії).
За ступенем складності: прості, середньої складності, складні, підвищеної складності.
За вимогою: на знаходження невідомого, на доведення, на конструювання.
За способом розв’язування: експериментальні, обчислювальні, графічні.
Розглянуту класифікацію задач не можна вважати досить повною, оскільки одна й та ж задача може бути віднесена до різних груп, проте вона досить зручна в застосуванні. У цю класифікацію не ввійшли також якісні задачі.
У залежності від того, які логічні операції застосовуються при розв'язанні задач, розрізняють методи розв'язування - аналітичний, синтетичний, та аналітико-синтетичний.
Аналітичний метод полягає у розчленуванні задачі на кілька простіших задач. Розв'язування починають з шуканої величини. У результаті аналізу відшукують закономірність, що зв'язує шукану величину з заданими. Якщо в закономірність входять крім шуканої величини інші невідомі, то шукають інші закономірності, що зв'язують їх з відомими в умові задачі. Розрахункова формула одержується як синтез окремих закономірностей.
При синтетичному методі послідовно виявляють зв'язки величин, які дані в умові, з іншими до тих пір, поки в рівняння не ввійде тільки одна шукана невідома величина. Отже, на відміну від аналітичного методу, де починають з шуканої величини, в синтетичному методі починають з величин, заданих в умові задачі.
У чистому вигляді аналітичний і синтетичний, як окремі, методи майже не застосовуються. При розв'язуванні задач використовують, як правило, і аналіз і синтез, тобто застосовують аналітико-синтетичний метод.
У залежності від математичного апарату, що застосовується при розв'язуванні задач, виділяють такі способи розв'язування обчислювальних задач: арифметичний, алгебраїчний, геометричний.
Алгебраїчний спосіб ґрунтується на використанні фізичних формул для складання рівнянь, з яких визначається шукана фізична величина.
Замість геометричного способу вживають термін геометричний прийом. Він полягає в застосуванні при розв'язуванні задач геометричних і тригонометричних властивостей фігур.
Розв'язування задач різних типів має свою специфіку, проте в педагогічній практиці виробилась певна послідовність розв'язування задач багатьох типів:
- читання умови задачі та з'ясування змісту нових термінів і виразів, повторення умови задачі учнями;
- короткий запис умови задачі, виконання необхідних малюнків, схем, графіків (усі фізичні величини мають бути виражені в одиницях СІ);
- аналіз умови задачі, в ході якого з'ясовуються її фізична суть, тобто з'ясовуються фізичні явища, процеси і стани системи та відновлюються в пам'яті учнів фізичні закони та формули, які потрібні для розв'язку задачі;
- складання плану розв'язку задачі;
- вираження зв'язків між шуканим і даними величинами у вигляді формул;
- розв'язування системи рівнянь для одержання кінцевої формули для розрахунку;
- обчислення шуканої величини;
- аналіз одержаних результатів;
- пошук і аналіз інших шляхів розв'язку задачі.
При розв'язуванні конкретних задач деякі етапи загальної схеми розв'язку задач можуть бути випущені.
Останнім часом для розв'язування задач використовують алгоритмічні прийоми та метод графів.
Методика розв'язування якісних та експериментальних задач має свою специфіку.
Організаційні форми розв'язування задач на уроках можуть бути такі:
- Розв'язування задач на дошці вчителем. Так чинять тоді, коли потрібно показати хід розв'язку типової задачі або розв'язати складну задачу. Вчитель залучає учнів до аналізу задачі з метою їх активізації.
- Аналіз задачі і відшукання ходу розв'язку проводять колективно, а потім один з учнів записує розв'язок задачі на дошці, а інші у своїх зошитах. При розв'язуванні складної задачі біля дошки може працювати кілька учнів почергово. Активність і самостійність учнів при такій організації роботи невисока, тому вчитель має постійно звертатись до класу з запитаннями, а наприкінці потрібно, щоб учні повторили хід міркувань і розв'язку задачі.
- Учні після колективного обговорення ходу розв'язку задачі або й без нього розв'язують задачу самостійно. Активність і самостійність учнів досить високі, але вони розв'язують задачі неодночасно, що створює деякі проблеми. Вчитель слідкує за ходом розв'язування задачі, консультує учнів, звертає увагу на недоліки та помилки, допомагає їх виправити.
1.2.Поради для учня
При вивченні елементарної фізики розв’язування задач має виключно велике значення. Задачі дають можливість зрозуміти та запам’ятати основні закони фізики, розвивають навички застосування отриманих знань для розв’язування конкретних проблем, що мають практичне та пізнавальне значення.
В основі кожної фізичної задачі лежить той або інший прояв загальних законів фізики. Тому, перед тим як приступити до розв’язування задач якогось розділу фізики, рекомендується скрупульозно опрацювати теорію питання. Без твердих знань теорії самостійно не можна розраховувати на успішний результат розв’язування і аналіз навіть порівняно простих задач, не кажучи уже про більш складні.
Всі задачі, незалежно від способу подання умови задачі, слід розв’язувати в загальному вигляді. При такій формі розв’язування залишаються ясними сліди законів, а самі викладки дають можливість перевірити любу частину рішення і виключити можливі помилки. Отримавши відповідь у вигляді алгебраїчної формули чи рівняння, його можна проаналізувати, установити характер та границі змін шуканої величини і функцій, через які вона виражена. Крім цього, і це, мабуть, головне, указаний спосіб розв’язування дає можливість виробити загальні прийоми розв’язування задач по кожному розділу.
Ознайомившись з умовою задачі, ніколи не варто загострювати увагу на шуканій величині і тим паче зразу її знайти. Варто пам’ятати, що першою ціллю розв’язання є те, щоб звести задачу від фізичної до математичної, записавши всі умови формулами. Для цього потрібно перш за все чітко уявити всі фізичні явища, про які йдеться в умові задачі, установити, які фізичні закони лежать в основі даного явища, пригадати математичну форму запису цих законів.
Для кращого розуміння умови задачі бажано зробити схематичний малюнок. Якщо при аналізі виявиться, що необхідно використовувати величини, яких в умові немає, то ці величини потрібно ввести в розв’язання.
Добре проаналізувати всі відомі величини.
За допомогою фізичних законів установити математичний зв’язок між всіма величинами. Отримаєте одне або кілька рівнянь – задача зведена до математичної.
Перед розв’язуванням складеної системи рівнянь переконайтесь в тому, щоб кількість невідомих дорівнювала кількості рівнянь.
Необхідно перевірити розмірність виведеної формули.
Отримавши результат в загальному вигляді, можна переходити до обчислень, пам’ятаючи, що всі величини повинні бути виражені в одній системі одиниць.
Перша частина розв’язування більшості фізичних задач розрахункового характеру зводиться спочатку до складання алгебраїчних рівнянь, які представляють собою математичні вирази законів фізики, що лежать в основі явищ, про які йдеться в задачі. В результаті таких записів маємо одне або декілька рівнянь (формул), що містять шукану величину у вигляді одного із невідомих, і фізична задача таким чином приводиться до математичної. Її подальше розв’язування заключається в тому, щоб із отриманої системи рівнянь знайти ті чи інші величини, які в даній задачі вважаються невідомими, і виконати числові розрахунки.
Запис системи рівнянь, які повністю відображають даний фізичний процес, являється однією із основних труднощів розв’язування майже всіх задач з фізики. Та більшість учнів мають достатні знання та вміння з алгебри, що дає можливість при умові добросовісного вивчення фізичних закономірностей, справитись з цією проблемою.
1.3.Памятка для учнів
Як розв'язувати фізичні задачі
Розв’язування фiзичних задач, як правило, має три етапи дiяльностiучнiв:
1)аналiзу фiзичної проблеми або опису фізичної ситуацiї;
2)пошуку математичної моделi розв’язку;
3)реалiзацiї розв’язку та аналiзу одержаних результатiв.
На першому етапi фактично вiдбувається побудова фiзичної моделi задачi, що подана в її умовi:
• аналiз умови задачi, визначення вiдомих параметрiв i величин та пошук невiдомого;
• конкретизацiя фiзичної моделi задачi за допомогою графiчних форм (малюнки, схеми, графiки тощо);
• скорочений запис умови задачi, що вiдтворює фiзичну модель задачi в систематизованому виглядi.
На другому, математичному етапi розв’язування фiзичних задач вiдбувається пошук зв’язкiв i спiввiдношень мiж вiдомими величинами i невiдомим:
• вибудовується математична модель фiзичної задачi, робиться запис загальних рiвнянь, що вiдповiдають фiзичнiй моделi задачi;
• враховуються конкретнi умови фiзичної ситуацiї, що описується в задачi, здiйснюється пошук додаткових параметрiв (початковi умови, фiзичнi константи тощо);
• приведення загальних рiвнянь до конкретних умов, що вiдтворюються в умовi задачi, запис спiввiдношення мiж невідомими і відомими величинами у формі часткового рівняння.
Саме для реалізації цього етапу необхідні не тільки знання фізики, а ще й глибокі знання математики. Математики не на рівні таблички множення та правил знаходження невідомого компонента, а часто знань похідної, функції, інтеграла. Мета даного посібника допомогти в вирішенні цієї проблеми.
На третьому етапi здiйснюються такi дiї:
• аналiтичне, графiчне або чисельне розв’язання рiвняння вiдносно невiдомого;
• аналiз одержаного результату щодо його вiрогiдностi й реальностi, запис вiдповiдi;
• узагальнення способiв дiяльностi, якi властивi даному типу фiзичних задач, пошук iнших шляхiв розв’язку
Слiд зазначити, що в навчаннi фiзики важливою формою роботи з учнями є складання ними задач, якi за фiзичним змiстом подiбнi до тих, що були розв’язанi на уроцi, наприклад обернених задач. Цей прийом досить ефективний для розвитку творчих здiбностей учнiв, їхнього розумового потенцiалу.
ІІ.ГРАФІКИ ТА ВЕКТОРИ

2.1. Графіки
Застосування графіків у фізиці
Графік – це лінія, побудована в системі координат (графіком може бути пряма, парабола, гіпербола та будь-яка лінія).
Система координат – це дві взаємно перпендикулярні прямі (їх називають осями координат).
Точку перетину координатних осей називають початком координат.
Осі підписують (біля стрілки) буквами, якими позначаються фізичні величини.
Обов’язково указують одиниці вимірювання фізичних величин (біля стрілки), якщо одиниці не указані, то графік схематичний.
![]() На кожній осі вибирають одиничні відрізки (одиничні відрізки на різних осях можуть бути різними).
На кожній осі вибирають одиничні відрізки (одиничні відрізки на різних осях можуть бути різними).
х,м
![]()
![]()
![]()
![]()
![]() t,c
t,c
Графік дає змогу виявити залежність між фізичними величинами. А саме:
Прямо пропорційна залежність –
у скільки разів змінюється одна величина у стільки ж й інша ( обидві величини одночасно збільшуються або одночасно зменшуються ).
Графік – пряма, що проходить через початок координат.
Лінійна залежність –
при збільшенні (зменшенні) однієї величина збільшується (зменшується) інша, але не в однакову кількість разів.
Графік – пряма, що не проходить через початок координат.
Обернено пропорційна залежність –
у скільки разів збільшується (зменшується) одна величина у стільки ж разів зменшується (збільшується) інша.
Графік – гіпербола (вітка гіперболи).
Квадратична залежність -
при збільшенні (зменшенні) однієї величини в n раз інша величина збільшується (зменшується) в n в квадраті раз.
Графік – парабола.
Якщо фізична величина залишається незмінною, то графіком буде пряма перпендикулярна до осі, вздовж якої відкладається дана фізична величина.
Графічний спосіб розв’язування задач не дуже точний, але він являється наочним, а іноді і єдино можливим способом розв’язати задачу.
Часто графічний спосіб використовують при дослідженні невідомих закономірностей, при визначенні залежностей між фізичними величинами, для запису формул та математичних співвідношень між величинами, при виконанні лабораторних робіт, тобто графічний спосіб являється невід’ємною частиною дослідницького апарату фізики.
Та будьте уважними при використанні графіків і формул. Далеко не завжди математична закономірність між величинами співпадає з правилами та законами фізики.
Наприклад, закон Ома для ділянки кола звучить так:
cила струму на ділянці кола прямо пропорційна напрузі та обернено пропорційна опору I = U/R . В даному випадку закон фізики повністю співпадає з математичною залежністю між величинами. А от формули отримані із цього закону R = U/I, U = I R не відображають фізичних реалій. Або ніяк не можна стверджувати, що густина речовини прямо пропорційна масі p = m/V, хоча з точки зору математики ви були б праві.
Тому треба бути обережним та уважним, коли робиш висновки на основі графіка.
2.2 Графіки в механіці
Графік швидкості v(t) – це лінія, побудована в осях t,v (на першому місці указують величину, якою позначають горизонтальну вісь, на другому – вертикальну, як правило).
Швидкість - векторна величина (має не тільки величину, а і напрям), основна одиниця вимірювання – м/с (метр за секунду).
Швидкість може бути додатньою (мати знак „+”), якщо її напрям співпадає з вибраним, а може бути від’ємною (мати знак „-”), якщо її напрям протилежний до вибраного напрямку.
Графіком швидкості рівномірного прямолінійного руху є горизонтальна пряма (перпендикулярна до осі v ).
v =const
Швидкість не змінюється.
![]() v,м/с
v,м/с
![]() v>0
v>0
![]()
t,c
![]() v<0
v<0
Графіком швидкості прямолінійного рівноприскореного руху є пряма не паралельна осі t.
v = const
v = vо + at
Швидкість змінюється.
![]()
 v,м/с
v,м/с


![]() 0 t,c
0 t,c
![]()
Точка перетину графіка швидкості з віссю v - це початкова швидкість v , з віссю t - показує час, коли швидкість дорівнює нулю.
![]()
 Якщо графік швидкості напрямлений вверх , то прискорення а додатнє.
Якщо графік швидкості напрямлений вверх , то прискорення а додатнє.
v,м/с
t,c
![]()
Якщо графік швидкості напрямлений вниз, то прискорення а від’ємне.
![]()
v,м/с

![]()
![]() t,c
t,c
Швидкість та прискорення мають однакові
знаки (напрямлені в одну сторону) –
 швидкість зростає (збільшується).
швидкість зростає (збільшується).
![]()
![]()
v,м/с v,м/с
![]()
![]() 0 0
0 0
 t,c t,c
t,c t,c
Швидкість vо додатня Швидкість vо від’ємна
(має знак „+”) (має знак „-”)
Прискорення додатнє Прискорення від’ємне
( має знак „+”) (має знак „-”)
Швидкість та прискорення мають різні
знаки (напрямлені в протилежні сторони) –
швидкість спадає (зменшується).
![]()
![]() v,м/с v,м/с
v,м/с v,м/с
![]()
 t,c
t,c
![]() t,c
t,c
Швидкість vо додатня Швидкість vо від’ємна
(має знак „+”) (має знак „-”)
Прискорення від’ємне Прискорення додатнє
(має знак „-”) (має знак „+”)
Графік швидкості дає можливість визначити переміщення при любому виді руху. Для цього достатньо обчислити
( якщо відомий характер руху і його закони ) або виміряти
(якщо характер руху або його закони невідомі ) швидкості при різних значеннях часу і побудувати графік швидкості.
Площа фігури, обмеженої віссю t , графіком швидкості та вертикальними прямими t1 і t 2 , чисельно дорівнює переміщенню за даний час при даному виді руху.
![]()
![]() v,м/с v,м/с
v,м/с v,м/с
![]()
![]()
![]()
![]() 0 0
0 0
![]() t1 t 2 t,c t1 t 2 t,c
t1 t 2 t,c t1 t 2 t,c
![]()
![]() v,м/с v,м/с
v,м/с v,м/с
![]()
![]()
![]()

![]()
![]()
![]()
![]() 0 0
0 0
t1 t2 t,c t1 t2 t,c
Графік руху x(t) - це лінія, побудована в осях t, х.
Графіком руху рівномірного прямолінійного руху є пряма.
X= Xo + V t
![]()
![]()
 x,м x,м
x,м x,м
![]()
![]() 0 0
0 0
t,c t,c
Початкова координати дорівнює Початкова координата
нулю, тіло рухається у вибраному не дорівнює нулю, тіло
напрямку. рухається у вибраному
напрямку.
![]()
![]() x, м x,м
x, м x,м
![]()
![]()
t,c t,c
Початкова координата дорівнює Початкова координата
нулю, тіло рухається проти не дорівнює нулю, тіло
вибраного напрямку. рухається проти вибраного
напрямку.
Точка перетину графіка з віссю х – це початкова координата, з віссю t - час, коли координата дорівнює нулю (тіло в початку координат).
Графіком руху прямолінійного рівноприскореного руху є парабола.
x = xo + vo t + at² /2
![]()
![]()
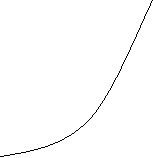 x,м x,м
x,м x,м
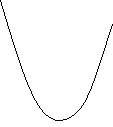
![]()
![]()
t,c t,c
х = 0, v = 0 x > 0, v < 0
![]()
![]() x,м x,м
x,м x,м
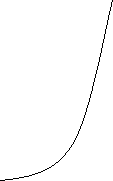
![]()
![]()
![]() t,c t,c
t,c t,c
x < 0, v > 0 x > 0, v < 0
![]()
![]() x,м x,м
x,м x,м
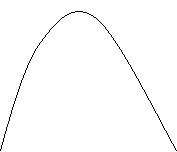

![]()
![]() t,c
t,c
t,c
x < 0, v > 0 x = 0, v = 0
2.3 Розв’яжи сам !!
1.Із двох точок А і В, розташованих на відстані 90 м, одночасно в одному напрямі почали рух два тіла. Тіло, що рухалось із точки А, мало швидкість 5 м/с, а із точки В – швидкість 2 м/с. Через який час перше тіло наздожене друге? Яке переміщення здійснить кожне тіло? Задачу розв’язати аналітично і графічно.
2.Визначити за графіком характер руху. Записати рівняння швидкості для кожної ділянки графіка. Визначити переміщення за весь час руху.
![]() s,м
s,м
![]()

![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]() 10
10
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 10
10
t,c
3.Тіло падає з висоти 490 м. Визначити переміщення за останню секунду падіння. Побудувати графіки швидкості та прискорення.
- Тіло рухається вздовж осі Х так, що залежність x(t) = 6 – 3t + 2t
Побудувати графіки переміщення, швидкості, прискорення. Знайти середню швидкість і прискорення за перші 4 секунди.
- За даними графіками побудувати графіки швидкості.
![]()
![]()
![]() s,м s,м s,м
s,м s,м s,м
![]()
![]()
![]()

![]()
![]()
![]()
![]() 20
20
![]()
![]() 10 10
10 10
![]()
![]()
![]()
![]() t,c t,c t,c
t,c t,c t,c
10
6.За даним графіком швидкості побудувати графіки прискорення та переміщення.
![]()
v,м/с

![]()

![]()
![]()
![]()
![]()
![]() 10
10
![]()
![]()
![]()
![]()
![]()
5 t,c
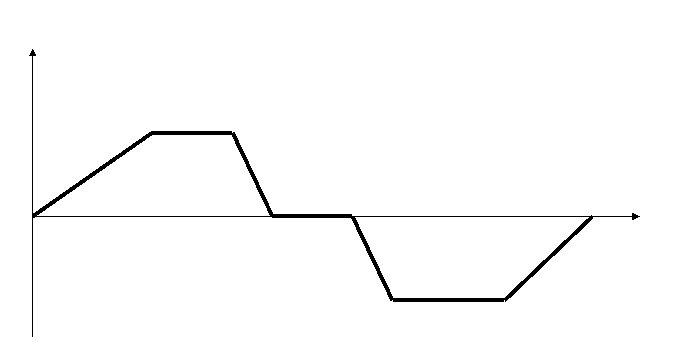
7.Як рухався мотоцикліст, графік швидкості руху якого показано на графіку?
8.Кабіна ліфта піднімається протягом 4 с рівноприскорено, набуваючи швидкість 4м/с. З цією швидкістю кабіна рухається 8 с, після чого 3 с рівносповільнено. Побудувати графік швидкості, прискорення і переміщення.
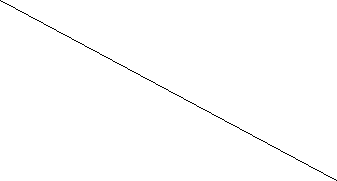
9.Проаналізувати за графіком рух. Побудувати графік прискорення.
![]()
v,м/с
![]()
![]()
![]() 2
2
![]()
![]()
![]()
![]()
![]()
1 t,c
![]()
![]()
2.4 Графіки в молекулярній фізиці та термодинаміці..
Графіки ізопроцесів
Ізопроцесами називають процеси, що відбуваються при незмінному макропараметрі .
Ізотермічний процес - це процес, що відбувається при незмінній температурі T = const
Графіком ізотермічного процесу є ізотерма.
В різних системах координат ізотерма має різний вигляд.
![]()
![]()
![]()
![]() p T
p T
![]()
![]()
![]()
![]()
![]() T V
T V
Ізотерма в осях рT і TV - це пряма перпендикулярна до осі Т.
![]() p
p
![]()
V
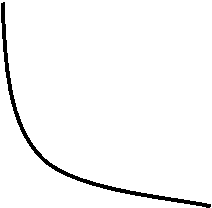
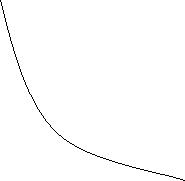
В осях рV ізотерма – це вітка гіпербо
![]()
![]()
![]()
![]()
![]()
![]() V V
V V
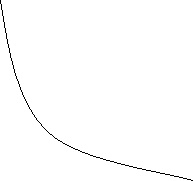
T2
T1
![]()
![]()
T1 T2 T p
T2 > T1
Правіше розташована ізотерма Вище розташована ізотерма
при вищій температурі.
Ізобарний процес - це процес, що відбувається при незмінному тиску p = const. Графіком ізобарного процесу є ізобара.
В різних системах координат ізобара має різний вигляд
![]()
![]()
![]()
![]() p p
p p
![]()
![]()
![]()
![]()
V T
Ізобара в осях Tp і Vp - це пряма перпендикулярна до осі р
![]() V
V


![]()
Т
Ізобара в осях TV-пряма, що проходить через початок координат.
![]()
![]()
![]() V V p1
V V p1
![]()

 p2
p2
![]()
![]()
![]()
![]()
![]()
![]() p1 p2 p T
p1 p2 p T
p2 > p1
Правіше розташована ізобара Нижче розташована ізобара
при більшому тиску
Ізохорний процес - це процес, що відбувається при незмінному об’ємі V = const. Графіком ізохорного процесу є ізохора.
В різних системах координат ізохора має різний вигляд.
Ізохора в осях Vp, TV - це пряма перпендикулярна до осі V.
![]()
![]()
![]()
p V
![]()
![]()
![]()
![]()
![]()
V T
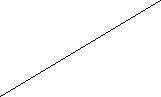
Ізохора в осях Tр-пряма, що проходить через початок координат.
![]() p
p

![]()

Т
![]()
![]() р р
р р
![]()
![]()

V1
![]()
 V2
V2
![]()
![]()
![]()
![]()
V1 V2 V T
V 2 > V1
Правіше розташована ізохора Нижче розташованаізохора
при більшому об’ємі
Графічний спосіб обчислення роботи в термодинаміці.
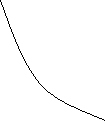
Робота чисельно дорівнює площі фігури, обмеженої графіком даного ізопроцесу, побудованим в осях Vp, віссю V і вертикальними прямими V1 і V2 .
![]()
![]()
![]()
![]()
р р р
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
V1=V2 V V1 V2 V V1 V2 V
Ізохора Ізобара Ізотер
2.5 Розв’яжи сам!!
![]()
![]()
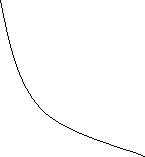
![]() 1.Підписати координатну вісь.
1.Підписати координатну вісь.
![]()
![]()
![]()
![]()
![]()
![]()
p T T
ізотерма ізохора ізобара
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
ізотерма ізотерма ізотерма
2.Побудувати діаграму в осях pV і TV. Проаналізувати зміни тиску, об’єму і температури на кожній ділянці.
![]() Т
Т
![]()
![]()
![]()
р
3.Як змінюються параметри p, V, T при незмінній масі?
![]() p
p

![]()
Т
4.Побудувати графіки процесів у різних осях:
1) ізотермічне розширення газу;
2) ізобарне нагрівання;
3) ізохорне охолодження.
5.Порівняти:
тиск в точках 1 і 2, 1 і 3, 6 і 7,
об’єм в точках 1 і 2, 1 і 3, 5 і 7.
Температуру в точках 1 і 2, 2 і 3, 4 і 7.
V T
![]()
![]()



![]()
3
![]()
 4 7
4 7
2
![]()
![]() 1 5 6
1 5 6
![]()
![]()
![]()
![]() р
р
Р
6.Накреслити ізотерми для 0,5 г водню для температури 0 С і 100 С.
7.Як змінюється об’єм газу при переході 1 – 3?
![]() р
р

![]() 2 3
2 3
1
![]()
T
8.Знайти роботу газу і показати її на графіку.
![]() р
р
2 3
![]()
![]()
![]()
![]() p2
p2
![]()
![]()
![]()
![]() p1
p1
1 4
![]()
V1 V2 V
9.Система отримала 100 Дж теплоти. Обчислити роботу і зміну внутрішньої енергії при ізохорному, ізотермічному та ізобарному процесах. Зобразити роботу графічно.
2.6 Вектори
Застосування векторів у фізиці.
Фізичні величини, що мають напрям, називаються векторними.
Векторні величини можна зобразити за допомогою вектора.
![]() Вектор – це напрямлений відрізок
Вектор – це напрямлений відрізок ![]() Кожен вектор має:
Кожен вектор має:
початок;
модуль (величину, розміри, довжину );
напрям.
Початок – це точка.
Модуль визначається за формулою даної фізичної величини, або є відомим в умові задачі.
Напрям визначається за правилами даної векторної величини.
Векторні величини позначають буквою зі стрілкою зверху.
Наприклад, векторними величинами являються:
![]()
![]()
![]() Швидкість v Прискорення a
Швидкість v Прискорення a
![]()
![]()
![]() Переміщення s Сила F
Переміщення s Сила F
Імпульс тіла p Напруженість E
Пригадаємо правила додавання векторів.
Векторні величини відрізняються від скалярних. А отже і правила додавання векторів відрізняються від правил додавання звичайних чисел. Правила додавання векторів треба запам’ятати!
Вектори завжди додаються парами, незалежно від їх кількості, тільки по два.
1. Щоб додати два вектори, напрямлені вдовж однієї прямої, треба їх величини додати і результат направити в ту ж сторону
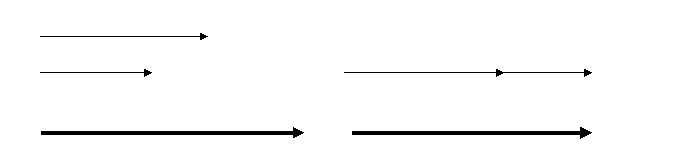
2. Щоб додати два вектори, напрямлені в протилежні сторони, треба від більшого вектора відняти менший і результат направити в сторону дії більшого вектора

Якщо вектори не напрямлені вздовж однієї прямої, то їх додають за правилами трикутника і паралелограма.
3.Якщо кінець першого вектора співпадає з початком другого, то їх додають за правилом трикутника.
Вектор, що дорівнює їх сумі виходить з початку першого вектора, а його кінець співпадає з кінцем другого вектора.
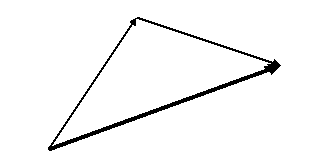
4.Якщо два вектори виходять з однієї точки, то їх додають за правилом паралелограма. Початок вектора, що дорівнює їх сумі, співпадає з початком векторів, а його кінець співпадає з кінцем векторів.
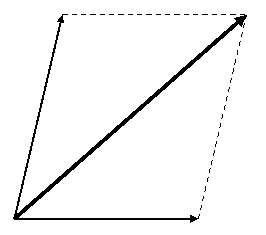
Векторні величини можна додавати інакше, використовуючи проекції векторів.
Щоб побудувати проекцію вектора на вибрану вісь, треба
провести перпендикуляри з початку та кінця вектора, відрізок, що сполучає точки перетину цих перпендикулярів з віссю і буде проекцією вектора на дану вісь. Проекція – скалярна величина.
Проекція вектора на вісь може бути:
додатною, якщо напрями вектора і даної осі співпадають

від’ємною, якщо вектор і вісь мають різні напрямки.
![]()
![]()
![]()
![]()
![]()
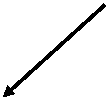
Проекція вектора може:
дорівнювати нулю, якщо вектор перпендикулярний до даної осі;
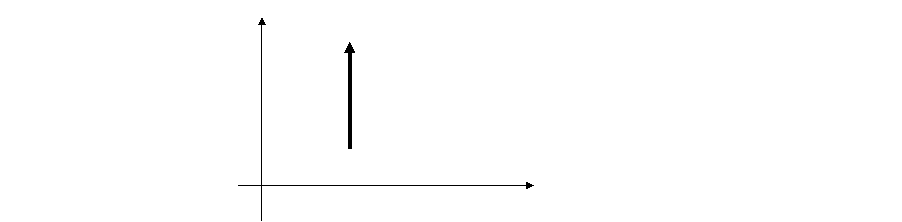
співпадати за величиною з вектором, якщо вектор паралельний до осі
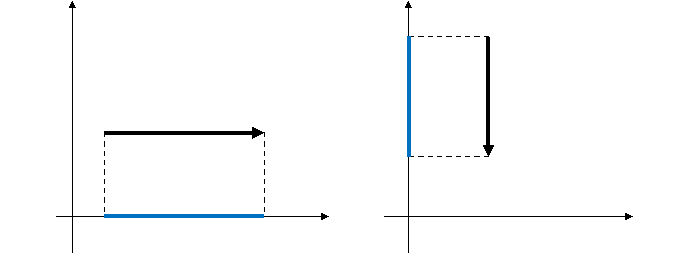
бути меншою за вектор, якщо він напрямлений під кутом до осі
(кут не дорівнює 90 або 180 градусів), тоді величина проекції визначається через тригонометричні функції (cos, sin, tg, ctg ) або інші правила геометрії.

Проекція вектора на вісь позначається такою ж буквою як і сам вектор, внизу біля цієї букви позначається вісь, на яку визначена проекція.
Наприклад:
вектора сили F на вісь X позначається Fx, на вісь Y - Fy, на вісь Z - Fz.
Кількість проекцій вектора залежить від кількості осей:
![]() якщо вісь одна ( на прямій ) – проекція одна ( на вісь X );
якщо вісь одна ( на прямій ) – проекція одна ( на вісь X );

![]() F
F
![]()
![]()
![]()
![]()
![]() Fx
Fx
X
![]() якщо дві осі – система координат ( в площині ) – дві проекції ( на осі X, Y ); Y
якщо дві осі – система координат ( в площині ) – дві проекції ( на осі X, Y ); Y
![]()
![]()
![]()

![]()
![]() Fy F
Fy F
![]()
![]()
![]()
![]()
![]() Fx
Fx
X
якщо три осі – просторова система координат ( в просторі ) – три проекції ( на осі X, Y, Z ).
![]() Y
Y

![]()
![]()
![]()
![]()

![]() F
F
Fy
![]()
![]()
![]()
 Fz
Fz
Fx X
Z
Використання проекцій зручне тим, що проекції – скалярні величини і додаються за звичайними правилами додавання чисел з однаковими та різними знаками.
Як легше додавати вектори – першим чи другим способом?
Це залежить від конкретного завдання, в одних випадках зручніше застосовувати правила додавання векторів, в інших – правила додавання проекцій.
Будьте уважні при додаванні векторів!
Розглянемо приклад.
Якщо ви додаєте два скалярні числа, наприклад 3 і 8, то отримаєте 11.
Якщо ж ви додаєте дві векторні величини 3 і 8, то результатом їх додавання може бути
5 ( якщо вектори напрямлені в протилежні сторони ),
11 ( якщо вектори напрямлені в одну сторону ),
Будь-яке число від 5 до 11, якщо вектори не напрямлені вздовж
однієї прямої ( напрямлені під кутом ).
Відповіддю на питання:
чому дорівнює сума векторів a і b , якщо a > b ?
Буде відповідь – вектор с, величина якого a – b < c < a + b
Розглянемо схематичну побудову деяких векторних величин у фізиці.
1.Сила тяжіння – прикладена до центру тіла і напрямлена вертикально вниз ( до центру Землі )

2.Вага – прикладена до опори або підвісу і напрямлена вертикально вниз
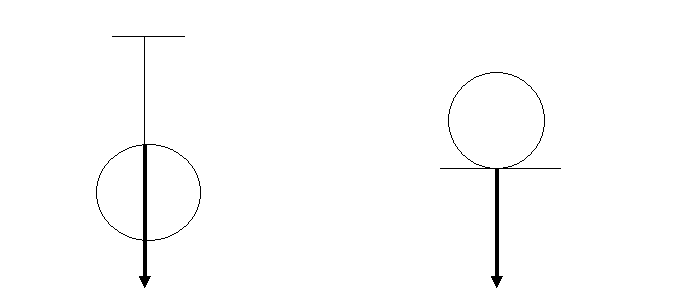
3.Сила Архімеда прикладена до центру тіла і напрямлена вертикально вверх
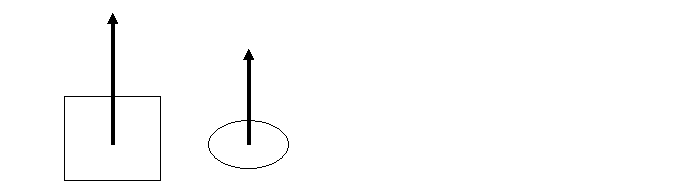
4.Сила натягу прикладена до тіла і напрямлена вздовж підвісу

5.Сила реакції опори прикладена до тіла і напрямлена перпендикулярно до опори в сторону тіла
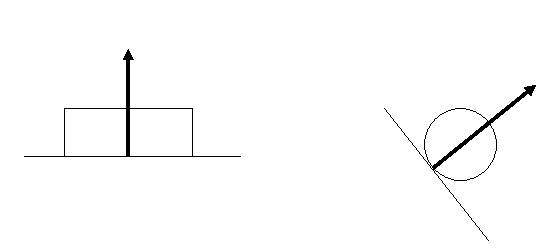
6.Сила тертя прикладена до тіла і завжди напрямлена проти руху
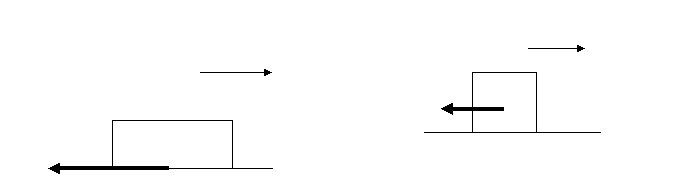
(тіла рухаються вправо)
Вектор можна множити на скаляр:
якщо скаляр – це додатнє число n , то величина вектора зміниться в n раз, напрям нового вектора буде співпадати з напрямом початкового вектора;
якщо скаляр – це від’ємне число m, то величина вектора зміниться в m раз, а напрям зміниться на протилежний.
![]()
![]()
![]()
![]() Віднімання векторів можна замінити на додавання протилежного вектора
Віднімання векторів можна замінити на додавання протилежного вектора
a – b = a + (-b).
Векторним добутком двох векторів називається вектор , який чисельно дорівнює добутку числових значень векторів , помноженому на синус кута між ними.
Скалярним добутком двох векторів називається скаляр, що дорівнює добутку числових значень векторів, помноженому на косинус кута між ними.
2.7 Розв’яжи сам !!
1.Два поїзди рухаються назустріч зі швидкостями 54 км/год і 72 км/год. Пасажир, який їде в першому поїзді помітив, що другий поїзд проходить повз нього за 8 с. Яка довжини другого поїзда?
2.Спортсмен перепливає річку завширшки h . Під яким кутом до течії він повинен пливти, щоб потрапити на протилежний берег за найкоротший час? Яку відстань він пропливе, якщо швидкість течії річки v1 , а швидкість спортсмена відносно води v2?
3.Пасажир іде зі швидкістю вверх по ескалатору, який рухається вниз зі швидкістю 1 м/с. З якою швидкістю треба рухатись пасажиру, щоб він залишався у стані спокою відносно людей, які стоять на іншому ескалаторі, що піднімається вверх з такою ж швидкістю?
4.Два автобуси рухаються зі швидкостями 54 км/год та 72 км/год.
Кут між швидкостями 60 градусів. З якою швидкістю автобуси роз’їжджаються?
5.Два однакові тіла масою M зв’язані між собою ниткою, перекинутою через блок з нерухомою віссю. На одне з тіл кладуть тягарець масою m. Визначити
1) з яким прискоренням рухатимуться тіла?
2) яким буде натяг нитки при русі тіла?
3) який тиск на вісь блока створюватиме нитка?
4) з якою силою тиснутиме тягарець на тіло M?
6.Динамометр, до якого підвішений шматок сплаву міді та срібла, показує в повітрі 2,41Н, а у воді 2,71Н. Визначити масу міді та срібла в цьому сплаві. Виштовхувальну силу повітря не враховувати.
ІІІ. ПОХІДНА ТА ІНТЕГРАЛ

3.1 З історії
Ключовим поняттям математичного аналізу, початки якого вивчають в школі, є поняття функції, границі, похідної та інтеграла.Термін " функція " вперше запропонував у 1692 р. видатний німецький філософі математик Готфрід Вільгельм Лейбіц ( 1646 – 1716)

для характеристики різних відрізків, що сполучають точки деякої кривої. Перше означення функції, яке вже н було пов’язане з геометричними уявленнями, сформулював Йоган Бернуллі ( 1667 – 1748 ) у 1718р.

Пізніше, у 1748. дещо уточнене означення функції дав учень
Й. Бернулі Леонард Ейлер ( 1707-1783 ).

Ейлеру належить символ функції f ( х ).
В означеннях Бернуллі і Ейлера функцію ототожнювали з аналітичним виразом, яким вона здається. Ейлер вважав також за можливе задавати одну й ту саму функцію на різних множинах різними аналітичними виразами. Ці так звані " Кусково – задані функції " широко застосовуються на практиці. Вже в часи Ейлера стало зрозумілим, що ототожнення функції з її аналітичним виразом
звужує саме поняття функції, бо, по-перше, одним і тим же виразом можна задати різні функції, по-друге, не завжди функцію можна задати аналітично. Вже Ейлер припускав можливість задавання функції лише графіком.
Дальший розвиток математичного аналізу і практичних застосувань математики привів до розширення поняття функції. У 1834 р. видатний російський математик М. І. Лобачевский ( 1792 – 1856 ) 
сформулював означення функції, в основу якого було покладено ідею відповідності: " Загальне поняття вимагає, щоб функцією від х називати число, яке дається для кожного х і разом з х поступово змінюється. Значення функції може бути задане або аналітичним виразом, або умовою, яка подає засіб випробування всіх чисел і вибору одного з них; або, нарешті, залежність може існувати і залишатися невідомою ".
Вже через три роки німецький математик Лежен Дріхле (1805 – 1859 ) зробив таке узагальнення поняття функції: " y є функція змінної x ( на відрізку
a≤ x ≤ b ), якщо кожному значенню x відповідає цілком повне значення y, причому не має значення, яким чином встановлена ця відповідність – аналітичною формулою, графіком, таблицею або навіть просто словами”.
У другій половині ХІХ ст.. після відкриття теорії множини до означення функції, крім ідеї відповідності, було залучено ідею множини, а тому сучасне означення функції формулюють так: " Відповідність між множинами x і y, при якій кожному елементу х множина Х відповідає певний елемент у множини У, називають функцією”.
У ХХ ст.. відбулося подальше розширення поняття функції, викликане потребами фізики. У 1930р. англійський фізик Поль Дірак (1902 – 1984)
ввів поняття так званої " дельта – функції ", а у 1936р. російський математик і механік С. Л. Соболєв ( 1908 – 1990 ) ввів більш широке поняття узагальненої функції, яке охоплює і дельта – функцію.
Отже, поняття функції продовжує розвиватися і розширюватися відповідно до потреб розвитку математичної науки та її практичних застосувань.
Походження поняття границі, на якому ґрунтується весь математичний аналіз і корені якого сягають глибокої давнини, пов’язане з обчисленням площ криволінійних фігур, об’ємів тіл, обмежених кривими поверхнями. Ідею границі вперше було використано стародавнім грецьким математиком IV ст. до н.е. Евдоксом Кнідським. Метод Евдокса, який був названий " метод вичерпування ", використовували Евклід, Архімед та інші вчені стародавнього світу.
Перше означення границі дав у середині XVII ст. англійський математик Джон Вал Ліс ( 1616 – 1703 ). Але тоді ще не було чіткого розуміння основних понять, пов’язаних з теорією границь. Зокрема, термін " нескінченно мала " розуміли як вказівку на розмір величини, а не характер її зміни.
Термін " границя " і відповідний символ lim вперше було введено англійським математиком і механіком Ісаком Ньютоном ( 1643 – 1727 ).

Строге означення границі і неперервності функції
сформулював у 1823 р. Французький математик Огюстен Луї Коші ( 1789 – 1857 ).
Означення неперервності функції ще раніше за Коші сформулював чеський математик Бернард Больцано
( 1781 – 1848 ). За цим означеннями на базі теорії дійсних чисел було здійснено строге обґрунтування основних положень математичного аналізу.
Відкриттю похідно і основ диференціального числення передували роботи французького математика і юриста П’’єра Ферма (1601 – 1665 ),

який у 1629 р. Запропонував способи знаходження найбільших і найменших значень функцій, проведення дотичних до довільних кривих, що фактично спиралися на застосування похідних. Цьому сприяли також роботи Рене Декатра ( 1596 – 1650 ),

який розробив метод координат і основи аналітичної геометрії. Лише в 1666 р. Ньютон і дещо пізніше Лейбніц незалежно один від одного побудували теорію диференціального числення. Ньютон прийшов до поняття похідної, розв’язуючи задачі про миттєву швидкість, а Лейбніц, - розглядаючи геометричну
задачу про проведення дотичної до кривої. Ньютон і Лейбніц досліджували проблему максимумів і мінімумів функцій. Зокрема, Лейбніц сформулював теорему про достатню умову зростання і спадання функції на відрізку.
Ейлер в роботі "Диференціальне числення "
( 1755р.) розрізняв локальний екстремум і найбільші та найменші значення функції на певному відрізку. Він перший почав використовувати грецьку букву Δ для позначення приросту аргументу ΔX=X2 – X1 і приросту функції ΔY = Y2 – Y1.
Позначення похідної у ' і f '( х ) ввів французький математик Жозеф Луї Лагранж ( 1736 – 1813).
Інтегральне числення і саме поняття інтеграла виникли з потреб обчислення площ плоских фігур і об’ємів довільних тіл. Ідеї інтегрального числення беруть свій початок у роботах стародавніх математиків. Проте це свідчить " метод вичерпування " Евдокса, який пізніше використав Архімед у ІІІ ст. до н. е.

Суть цього методу полягала в тому, що для обчислення площі плоскої фігури і, збільшуючи кількість сторін многокутника , знаходили границю, до якої прямували площі ступінчастих фігур. Проте для кожної фігури обчислення границі залежало від вибору спеціального прийому. А проблема загального методу обчислення площ і об’ємів фігур залишалась нерозв’язаною. Архімед ще явно не застосовував загальне поняття границі і інтеграла, хоча в неявному вигляді ці поняття використовувались.
У XVII ст.. Йоганном Кеплером ( 1571 – 1630 ),

який відкрив закони руху планет, було успішно здійснено першу спробу розвинути ідеї Архімеда. Кеплер обчислював площі плоских фігур і об’єми тіл, спираючись на ідею розкладання фігури і тіла на нескінченну кількість нескінченно малих частин. З цих частин у результаті додавання складалась фігура, площа якої відомо і яка дає змогу обчислити площу шуканої. На відміну від Кеплера, італійський математик Бонавентуро Кавальєрі 9 1598 – 1647 ), перетинаючи фігуру ( тіло ) паралельними прямими ( площинами ), вважав їх позбавленнями будь – якої
товщини, але додавав ці лінії. В історію математик увійшов так званий " принцип Кавальєрі ", за допомогою якого обчислювали площі і об’єми. Цей принцип дістав теоретичне обґрунтування пізніше за допомогою інтегрального числення. Для площ плоских фігур принцип кавальєрі формулювали так: якщо прямі деякого пучка паралельних прямих перетинають фігури Ф1 і Ф2 рівні.
Ідеї Кеплера та інших вчених стали тим ґрунтом, на якому Ньютон і Лейбніц відкрили інтегральне числення. Розвиток інтегрального числення продовжили Ейлер та П. Л. Чебишов ( 1821- 1894 ),

який розробив способи інтегрування деяких класів ірраціональних функції.
Сучасне означення інтеграла як границі інтегральних сум належить Коші. Символ ∫ ydx було введено Лейбіцем. Знак ∫ нагадує розтягнуту S ( першу букву латинського слова SUMMA – " сума "). Термін
”інтеграл” походить від латинського INTEGER – " цілий " і був запропонований у 1690р. Й. Бернуллі .

МАТЕМАТИЧНИЙ АПАРАТ ФІЗИКИ
3.2 Похідна
Нехай в деякому околі точки x0 визначена функція f. Якщо ми візьмемо довільне число x в цьому околі, то приріст аргументу (позначається Δx) в цьому випадку визначається як x−x0, а приріст функції (Δy) — як f(x)−f(x0). Тоді, якщо існує границя ![]() , то вона називається похідною функції f в точці x0.
, то вона називається похідною функції f в точці x0.
Похідною функцією даної функції називається функція, що в будь-якій точці області визначення дорівнює похідній даної функції в цій точці.
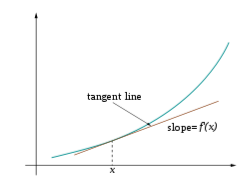
Диференціювання – це метод обчислення співвідношення приросту залежної змінної y по відношенню до приросту незалежної змінної x. Це співвідношення приростів називається похідною функції y по змінній x. Якщо говорити більш точно, залежність y від x означає, що y функція від x. Ця функціональна залежність часто позначається y = ƒ(x), де ƒ позначає функцію. Якщо x та y дійсні числа, і якщо графік функції y зображено відносно x, похідна дорівнює нахилу дотичної до цього графіка в кожній точці.
Найпростіший випадок коли y – лінійна функція від x, це означає що графік функції y відносно x пряма лінія. В такому випадку, y = ƒ(x) = m x + b, для дійсних чисел m та b, і нахил m визначається так
![]()
де символ Δ (грецька літера у верхньому регістрі дельта) – це є скорочення для "зміни в". Ця формула справедлива тому, що
y + Δy = ƒ(x+ Δx) = m (x + Δx) + b = m x + b + m Δx = y + mΔx.
З цього випливає, що Δy = m Δx.
Отримали точне значення нахилу прямої лінії. Якщо функція ƒ не лінійна (тобто графік функції не пряма лінія), тоді приріст y поділений на приріст x змінюється: диференціювання це спосіб обчислення точного значення відношення приростів для будь-якого значення x.
Співвідношення приростів як гранична величина
Дотична в точці (x, ƒ(x))
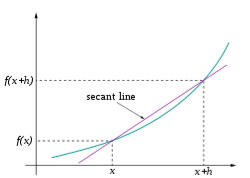
Січна лінія до кривої y= ƒ(x) задається точками (x, ƒ(x)) and (x+h, ƒ(x+h))
Дотична як границя січних ліній
Ідея полягає в тому, див. рисунки 1-3, щоб обчислити відношення приростів як граничну величину Δy / Δx коли Δx стає нескінченно малим.
Якщо використати позначення Лейбніца, тоді нескінченно малий приріст x позначається як dx, а похідна функції y по змінній x записується:
![]()
виглядає як відношення двох нескінченно малих величин. (Даний вираз читається так: "похідна функції y по змінній x"або "d y по d x")
Пояснення визначення
Нехай ƒ – функція дійсних чисел. В класичній геометрії, дотична до графіка функції ƒ для дійсного числа a була єдина лінія через точку (a, ƒ(a)), що не перетинається з графіком функції ƒ трансверсально, це означає що ця лінія не проходить крізь графік. Похідна функції y по змінній x в точці a, з геометричної точки зору, це нахил дотичної лінії до графіка функції ƒ в точці a. Нахил дотичної дуже близький до нахилу лінії, що проходить крізь точку (a, ƒ(a)) та іншу близьку точку на графіку, наприклад (a + h, ƒ(a + h)). Такі лінії називаються січними. Значення h близьке до нуля дає добре наближення для нахилу дотичної, а чим менше значення h, в загальному випадку, тим краще буде наближення. Нахил m січної лінії дорівнює різниці значень y для цих точок поділити на різницю значень x, тобто
![]()
Цей вираз — це відношення приростів Ісаака Ньютона. Похідна — це значення відношення приростів у випадку коли січні лінії наближаються до дотичної. Строго кажучи, похідна функції ƒ в точці a це границя:
![]()
відношення приростів коли h наближається до нуля, якщо така границя існує. Якщо границя існує тоді ƒ – диференційована в точці a. Тут ƒ′ (a) одне з кількох можливих позначень похідної (див. нижче)
Запишемо еквівалентний вираз, для похідної справедлива рівність
![]()
що також піддається інтуїтивному розумінню (див. рис.1), де дотична лінія ƒ в точці a дає найкраще лінійне наближення
![]()
для ƒ біля точки a (наприклад, для малих h). Якщо підставити 0 замість h у відношення приростів то отримаємо ділення на нуль, отже нахил дотичної лінії не можна обчислити таким способом. Натомість запишемо Q(h), відношення приростів як функцію від h:
![]()
Q(h) – це нахил січної лінії між точками (a, ƒ(a)) and (a + h, ƒ(a + h)). Якщо ƒ – неперервна функція, тобто якщо графік функції немає розривів, тоді Q також неперервна функція починаючи з точки h = 0. Якщо існує границя ![]() , тобто якщо існує спосіб обчислити значення для Q(0), це означає що графік функції Q неперервний, тоді функція ƒ диференційована в точці a, і її похідна в точці a дорівнює Q(0).
, тобто якщо існує спосіб обчислити значення для Q(0), це означає що графік функції Q неперервний, тоді функція ƒ диференційована в точці a, і її похідна в точці a дорівнює Q(0).
На практиці, існування неперервного продовження відношення приростів Q(h) в точці h = 0 показують по-іншому: міняють чисельник таким чином щоб скоротити h у знаменнику. Цей процес може бути довгим та нудним для складних функцій, тож в таких випадках використовують багато спрощень.
Приклад.Квадратна функція ƒ(x) = x² — диференційована в точці x = 3 і її похідна в цій точці дорівнює 6. Цього результату можна досягнути, якщо обчислити границю відношення приростів ƒ(3) при h прямує до нуля:
![]()
Тепер можемо обчислити границю, якщо підставимо замість h нуль:
![]()
Отже, нахил графіку квадратної функції в точці (3, 9) дорівнює 6, а її похідна в точці x = 3 дорівнює ƒ '(3) = 6. Узагальнюючи, якщо провести схожі обчислення то отримаємо, що квадратна функція в точці x = a дорівнює ƒ '(a) = 2a Неперервність і диференційованість
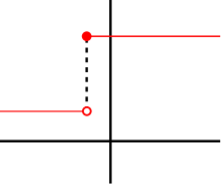
Ця функція не має похідної у вказаній точці, оскільки функція не є неперервна в цій точці.
Якщо y = ƒ(x) — диференційована в точці a, тоді ƒ також має бути неперервна а точці a. Для прикладу, виберемо точку a і нехай ƒ буде кроковою функцією, що дорівнює 1, для всіх x менших ніж a і дорівнює іншому значенню, скажімо 10, для всіх x, які більші або дорівнюють a. ƒ не має похідної в точці a. Якщо h — від'ємне, тоді a + h знаходиться на нижній сходинці функції, тоді січна лінія від a до a + h дуже круто піднімається вгору і якщо h прямує до нуля тоді нахил лінії прямує до нескінченності. Якщо h додатне, тоді a + h на верхній сходинці і січна лінія від a до a + h має нахил, що дорівнює нулю. Відповідно січні лінії не утворюють єдиний нахил, отже границя від відношення приростів не існує.
Функція абсолютної величини є неперервна, але від неї не можна отримати похідну в точці x = 0, оскільки нахил дотичної наближується до різних значень з різних боків від даної точки.
Проте якщо функція неперервна в точці, тоді вона не обов'язково диференційована в цій точці. Наприклад, функція абсолютної величини y = |x| є неперервною в точці x = 0, але не є диференційована в цій точці. Якщо h додатне, тоді нахил січної лінії від 0 до h дорівнює одиниці, якщо h від'ємне, тоді нахил січної лінії від 0 до h дорівнює -1. На графіку цю точку видно як «зубець» в точці x = 0. Навіть функції з графіком без «зубців» не є диференційовані в точці де дотична лінія є вертикальна: наприклад функція y = 3√x не є диференційована в точці x = 0.
Підведемо підсумки: щоб отримати похідну від функції ƒ необхідна умова щоб функція ƒ була неперервною, але тільки цього не достатньо.
Більшість функцій, що зустрічаються на практиці мають похідні у всіх точках, або майже у всіх точках. Раніше на початку вивчення математичного аналізу, багато математиків припускали, що неперервна функція диференційована в більшості точок. Для м’яких умов, наприклад якщо маємо монотонну функцію або Ліпщицову функцію це формулювання справедливе. Проте в 1872 Вейерштрас знайшов перший приклад функції, яка неперервна усюди, але не є диференційованою в жодній точці. Ця функція відома як Вейерштрасова. В 1931 році Стефан Банах довів, що множина функцій, які мають похідну хоча б в якійсь точці є множина першої категорії в просторі всіх неперервних функцій.[1]
Похідна
Середньою швидкістю зміни функції на проміжку ![]() називають відношення приросту функції до незалежної змінної, тобто
називають відношення приросту функції до незалежної змінної, тобто
![]() .
.
Границю середньої швидкості з приростом незалежної змінної, що прямує до нуля, тобто ![]() , називається швидкістю зміни функції в точці
, називається швидкістю зміни функції в точці ![]() . Її називають похідною. Похідну функції
. Її називають похідною. Похідну функції ![]() в точці
в точці ![]() позначають так:
позначають так: ![]() .
.
Механічний зміст похідної:
![]() Якщо задано функцію
Якщо задано функцію ![]() , за допомогою якої можна визначити положення точки для будь-якого моменту часу, то рух вважається заданим, а рівняння
, за допомогою якої можна визначити положення точки для будь-якого моменту часу, то рух вважається заданим, а рівняння ![]() – рівнянням руху.
– рівнянням руху.
Так, в момент часу ![]() точка знаходиться в точці М на відстані
точка знаходиться в точці М на відстані ![]() . Розглянемо момент
. Розглянемо момент ![]() , коли точка знаходиться в точці М1 на відстані
, коли точка знаходиться в точці М1 на відстані ![]() від точки О. За час
від точки О. За час ![]() точка пройшла шлях
точка пройшла шлях ![]() із середньою швидкістю
із середньою швидкістю
![]() .
.
Границя середньої швидкості за проміжок часу ![]() , коли
, коли ![]() прямує до нуля, називається швидкістю точки в довільний момент часу. Отже:
прямує до нуля, називається швидкістю точки в довільний момент часу. Отже:
![]() .
.
Швидкість точки, що рухається в довільний момент часу , похідною від шляху за часом, а похідна швидкості за часом є прискоренням.
Похідна позначається як ![]() , що вимовляється «еф-штрих від ікс».
, що вимовляється «еф-штрих від ікс».
Функція, що має скінченну похідну в точці x, зветься диференційованою в точці x. Похідна також позначається, як відношення диференціалів ![]() . В фізиці для позначення похідних по часу використовують крапку над змінною, наприклад
. В фізиці для позначення похідних по часу використовують крапку над змінною, наприклад ![]() .
.
Позначення Лейбніца
Позначення похідної запропоноване Лейбніцом було одним з найперших. Воно широко використовується дотепер. Якщо вираз y = ƒ(x) розглядається як функціональна залежність між залежною і незалежною змінними. Тоді перша похідна позначається як:
![]()
похідні вищого порядку позначаються таким чином
![]()
для похідної n-го порядку y = ƒ(x) (по змінній x). Це є скорочення для багаторазового застосування оператора похідної. Наприклад,
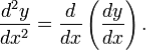
Через позначення Лейбніца ми можемо записати похідну функції y в точці x = a двома різними способами:
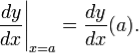
Позначення Лейбніца дає змогу вказувати змінну диференціювання (в знаменнику). Це особливо важливо для часткового диференціювання. В такому позначенні також легше запам’ятати ланцюгове правило:
![]()
Позначення Лагранжа
Позначення Лагранжа одне з найбільш поширених сучасних позначень для диференціювання, що вперше використав Жозеф-Луї Лагранж. Для позначення похідної використовують знак штрих, таким чином похідна функції ƒ(x) позначається ƒ′(x) чи просто ƒ′ подібним чином друга та третя похідна позначаються
![]() and
and ![]()
Починаючи звідси деякі автори застосовують римські цифри:
![]()
для четвертої похідної, тоді як інші автори ставлять цифру порядку похідної в дужки:
![]()
Останній запис узагальнює позначення ƒ (n) для похідної функції ƒ n-го порядку — таке позначення особливо зручне коли ми говоримо про похідну як про функцію, в цьому випадку застосування позначення Лейбніца може бути надто громіздким.
Позначення Ньютона
Детальніше: Нотація Ньютона
Позначення Ньютона для диференціювання, також називається точкове позначення, ставлять точку над назвою функції для позначення похідної. Якщо y = ƒ(t), тоді
![]() і
і ![]()
означає відповідно першу та другу похідну функції y по змінній t. Таке позначення застосовується майже виключно для похідних по часу, тобто незалежна змінна функції є часом. Воно дуже поширене у фізиці і математичних дисциплінах пов’язаних з фізикою, наприклад диференціальні рівняння. Хоча таке позначення стає проблематичним в користуванні для похідних високого порядку, на практиці потрібні тільки кілька перших похідних.
Обчислення похідної
Похідну функції можна, теоретично, обчислювати використовуючи границю відношення приростів. На практиці, достатньо знати похідні обмеженої кількості простих функцій, тоді можна обчислити більш складні випадки за допомогою правил диференціювання.
Похідні простих функцій
Під час розв’язування задач з фізики користуються такими похідними:
|
|
|
|
|
|
|
|
|
|
|
|
В більшості випадків для того щоб обчислити похідну потрібно знати похідні певних поширених функцій. Нижче наведено неповний перелік з похідних деяких найбільш уживаних функцій однієї дійсної змінної.
- Піднесення до степеня: Якщо
![]() ,
,
де r — будь-яке дійсне число, тоді
![]() ,
,
для будь-яких випадків коли визначена функція Наприклад, якщо r = 1/2, тоді
![]() .
.
тут функція визначена тільки для позитивних x. Якщо r = 0, це правило повторює правило константи.
- Експонента та Логарифм:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Приклад знаходження похідної за визначенням
Нехай є функція y=c, де c — деяка константа. Тоді при будь-якому x0 та при будь-якому Δx зміна (приріст) функції дорівнюватиме нулю, отже і похідна такої функції дорівнюватиме нулю.
Похідні вищих (старших) порядків
Поняття похідної довільного порядку задається рекурентно:
- похідна нульового порядку — сама функція
- похідна n-го порядку для натурального n, що більше 0, — похідна похідної (n−1)-го порядку
Іноді замість «похідна n-го порядку» говорять «n-а похідна».
Похідна n-го порядку функції f зазвичай позначається як f(n)(x)
- якщо n мале (1, 2, 3) — то використовується відповідна кількість рисок, f′(x), f′′(x), f′′′(x), вимовляється як «еф-штрих від ікс»; про другу — «еф-два-штрихи від ікс».
- Можна зустріти історичне позначення похідної за допомогою римської системи числення (перша похідна: f′(x), друга: fII(x), шістнадцята: fXVI(x)).
-
В фізиці також зустрічається позначення похідної другого порядку по часу у вигляді двох крапок над змінною:
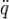 .
.
Геометричний зміст похідної
Значення похідної f'(x0) функції f у точці x0 дорівнює значенню кутового кофіціента дотичної до кривої y = f(x) у точці з абсцисою x0.
Рівняння дотичної до кривої y = f(x) у точці M(x0,y0) має вигляд:
![]()
y=f́(x)=tga
Фізичний зміст похідної
Похідна від шляху за часом дорівнює миттєвій швидкості руху матеріальної точки.
Похідна – це швидкість зміни фізичної величини
Швидкості зміни фізичної величини:
|
|
Означення |
Формула |
Похідна |
|
1. |
Швидкість руху – це швидкість зміни шляху |
v = s/t |
v = s´ (ω = φ′) |
|
2. |
Прискорення – це швидкість зміни швидкості |
a = Δv/Δt |
a = v´ (ε = ω′) |
|
3. |
Сила струму – це швидкість зміни заряду |
І = Δq/Δt |
І = q´ |
|
4. |
ЕРС – це швидкість зміни магнітного потоку |
ε = ΔФ/Δt |
ε = Ф´ |
Диференціювання може відбуватись не тільки по dt!
Використання похідної при виведенні рівняння електромагнітних коливань.
Запишемо рівняння закону збереження енергії для коливального контуру
Wел +Wм = const
Знайдемо похідні обох частин рівності.
(Wел +Wм)′ = const′
Похідна суми дорівнює сумі похідних, а похідна сталої дорівнює нулю.
(Wел) ′ +(Wм)′ = 0
Wел = q²/2C
Wм = LI²/2
(q²/2C)′ + (LI²/2) ′ = 0
Сталу можна виносити за знак похідної
2, С, L, ½
1/2C(q²)′ = L/2(I²)′
(q²)′ = 2q
(I²)′ =2I, але під час електромагнітних коливань в коливальному контурі заряд на конденсаторі та сила струму в котушці змінюються з часом, тому в даному випадку q та I є не просто величинами, а функціями від часу, іншими словами є складеними функціями з точки зору обчислення похідної, тому правильно не (q²)′ = 2q, а
(q²)′ = 2qq′ (похідна складеної функції дорівнює добутку похідної зовнішньої функції (q²)′ = 2q та похідної внутрішньої функції q′),
не (I²)′ =2I, а (I²)′ =2I І′
1/2C · 2qq′ = L/2 · 2I I′
1/C · qq′ = L· I I′
Використаємо І = q´ та І′ = q´′
1/C · qq′ = L· q´q´′
Поділимо праву та ліву частини рівняння на q´ та L
1/CL· q = q´′
q′′ = 1/CL· q
Ми отримали не тільки рівняння електромагнітних коливань, а і установили математичну залежність, за якою за зовнішнім виглядом рівняння можна установити чи є дане рівняння рівнянням коливань
Якщо друга похідна величини прямо пропорційна самій величині, то це рівняння коливань.
3.3 Розв'яжи сам!!
1.Рівняння руху тіла дано у вигляді х=15t + 0,4t². Визначити початкову швидкість та прискорення руху тіла, а також координату та швидкість тіла через 5с.
2.Залежність кута повороту радіуса колеса від часу
φ = 4+5t -t³. Знайти в кінці першої секунди обертання швидкість колеса, лінійну швидкість та повне прискорення точки, що лежить на ободі колеса. Радіус колеса 2см.
3.Потенціальна енергія тіла масою 0,5кг змінюється за законом W(х) = 6х² + 4х -2. Знайти прискорення при проходженні положення рівноваги.
4.Вивести рівняння електромагнітних коливань, використовуючи закон збереження енергії для коливального контуру.
3.4 Інтеграл
Інтеграл — центральне поняття інтегрального числення, узагальнення поняття суми для функції, визначеній на континуумі. Існує кілька різновидів визначених інтегралів: інтеграл Рімана, інтеграл Лебега, інтеграл Стілтьєса, тощо.
Визначений інтеграл дорівнює площі криволінійної фігури, обмеженої кривою
Інтеграл Рімана
Інтеграл Рімана — найпростіший із визначених інтегралів, є границею інтегральної суми. Для функції однієї змінної f(x), визначеній на відрізку [a,b] та певного розбиття R цього відрізку на відрізки [xi,xi + 1] інтегральна сума визнається як
|
SR = |
∑ |
f(ξi)(xi + 1 − xi), |
|
|
i |
|
де ![]() — будь-яка точка з відрізку.
— будь-яка точка з відрізку.
Якщо існує границя таких сум при прямуванні найбільшої довжини відрізку [xi,xi + 1] до нуля, то функція f(x) називається інтегрованою, а границя інтегральної суми називається інтегралом Рімана функції на відрізку [a,b] і позначається
![]() .
.
Інтеграл Рімана можна також визначити як границю сум Дарбу.
Інші визначення інтегралу розширюють клас інтегрованих функцій, включаючи в них функції, для яких границі інтегральних сум не існує.
Головна теорема інтегрального числення
Якщо у функції f(x) існує первісна F(x), то
![]()
Ця формула називається формулою Ньютона-Лейбніца, або основною формулою інтегрального числення.Обчислення первісної – це обернена задача знаходження похідної.
Застосування визначеного інтеграла в фізиці і техніці
(Властивості визначеного інтеграла. Застосування визначеного інтеграла для обчислення площ фігур. Застосування визначеного інтеграла для обчислення об’ємів тіл.)
Якщо нижня і верхня границі функції співпадають, то інтеграл дорівнює нулю.
Якщо в інтеграла поміняти місцями нижню і верхню границі інтегрування, то значення інтеграла зміниться на протилежне.
Щоб обчислити визначений інтеграл від функції зі сталим множником, можна сталий множник винести за знак інтеграла.
Визначений інтеграл від суми функцій дорівнює сумі інтегралів з тими ж границями інтегрування від кожного доданка.
Визначений інтеграл від заданої функції з границями інтегрування, що є протилежними числами, дорівнює:
- якщо функція непарна, то нулю;
- якщо функція парна, то подвоєному інтегралу від тієї ж функції, але від нуля до заданої верхньої границі інтегрування.
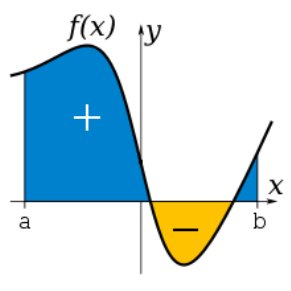
Якщо фігура, площу якої треба знайти, обмежена графіками функцій f(x) (обмежує зверху) і g(x) (обмежує знизу), то для обчислення площі такої фігури треба обчислити інтеграл від різниці цих функцій на заданому проміжку.
Якщо криволінійна трапеція обмежена зверху різними функціями, то площа криволінійної трапеції дорівнює сумі площ криволінійних трапецій, обмежених зверху кожною з цих функцій.
Якщо фігура розміщена у від’ємній півплощині відносно осі абсцис, то її площу можна знайти як модуль визначеного відповідного інтеграла.
Для обчислення площ фігур, обмежених графіками заданих функцій, використовуємо таку схему:
- - Побудувати фігуру, площу якої треба знайти в координатній площині;
- - Знайти абсциси точок перетину графіків заданих функцій.
- - Скласти й обчислити інтеграл від різниці верхньої і нижньої функцій із границями інтегрування, які дорівнюють абсцисам точок перетину графіків функцій.
Зверніть увагу! Нижньою границею інтегрування треба брати лівий кінець відрізка, на якому визначається криволінійна трапеція.
Використовують інтеграл у фізиці!
Об’єм тіла, утвореного обертанням навколо осі абсцис криволінійної трапеції, обмеженої зверху графіком неперервної невід’ємної функції, дорівнює визначеному інтегралу квадрата функції, помноженого на константу π.
Робота змінної сили вздовж осі абсцис на заданому проміжку дорівнює визначеному інтегралу від функції сили.
Шлях, що проходить тіло зі змінною швидкістю за проміжок часу, дорівнює інтегралу від функції швидкості.
Маса стержня із змінною густиною з заданою довжиною дорівнює визначеному інтегралу від функції густини.
3.5 Розв'яжи сам!!
1.Швидкість тіла виражається формулою v=2,5+0,2t. Знайти переміщення тіла через 20с від початку руху.
2.Тіло обертається так, що залежність кутової швидкості від часу задається рівнянням ω =2+0,5t. Знайти повне число обертів, виконаних тілом за 20 с після початку обертання.
3.Вантаж масою 5 кг падає з деякої висоти і досягає поверхні землі за 2,5с. Знайти роботу, виконану вантажем.
4.Азот масою 10г розширюється ізотермічно, при температурі -20ºС, змінюючи тиск від 202 до 101 кПа. Визначити роботу розширення, зміну внутрішньої енергії азоту та кількість переданої йому кількості теплоти.
5.Визначити масу міді, що виділилась на катоді за 10с при проходженні через розчин мідного купоросу струму, сила якого рівномірно збільшується від 0 до 4А.
ІV. Список використаної літератури
- Активизация познавательной деятельности учащихся при изучении физики. Пособие для учителей. - М.: Просвещение, 1983. -160с.
- Розв'язування задач з фізики. Практикум. За заг. ред. Є.В.Коршака. - К.: Вища школа, 1986. - 132 с.
- Зверева Н.М. Активизация мышления учащихся на уроках физики. - М: Просвещение, 1980. - 112 с.
- Альбін К.В. та ін. Методика викладання фізики. - К.: Вища школа, 1970.-300 с.
- http://uk.wikipedia.org/wiki/%D0%86%D0%BD%D1%82%D0%B5%D0%B3%D1%80%D0%B0%D0%BB
- http://www.fizika.net.ua/index.php?newsid=14
- http://www.4uth.gov.ua/education/fizika/r4.htm
- http://ua.textreferat.com/referat-13406.html

1


про публікацію авторської розробки
Додати розробку