Навчальний посібник "Геометрія 7 клас ІІ семестр"

Тема №4. Рівнобедрений трикутник. Прямокутний трикутник

 

Урок №1

Рівнобедрений трикутник. Прямокутний трикутник

«Ні один живописець не може

писати, не знаючи геометрії»

Л. Альберті

Питання

1. Рівнобедрений трикутник.
2. Прямокутний трикутник.
3. Нерівності трикутника.

Література

Істер О.С. Геометрія: підручник для 7 класу загальноосвітніх навчальних закладів – К.: Генеза, 2015 рік, розділ 3, § 14 – 15, стор. 82 – 92, § 19 – 20, стор. 108 – 126.

Рівнобедрений трикутник
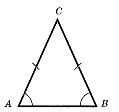
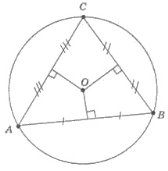
1.1	Трикутник, у якого дві сторони рівні, називається рівнобедреним.	АС = ВС – бічні сторони АВ - основа
1.2	Рівні сторони рівнобедреного трикутника називаються бічними сторонами, а третя сторона – основою.
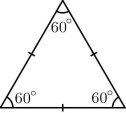
1.3	Трикутник, у якого всі сторони рівні, називається рівностороннім.	АВ = ВС = АС
1.4	Трикутник, у якого всі сторони мають різні довжини, називають різностороннім.	В      А                                      С
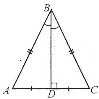
1.5	Теорема. У рівнобедреного трикутника кути при основі рівні, а бісектриса, проведена до основи, є медіаною і висотою.	, ВК – бісектриса, медіана, висота
1.6	Теорема. Якщо у трикутнику два кути рівні, то він рівнобедрений.
1.7	Наслідок. У трикутнику проти рівних сторін лежать рівні кути, а проти рівних кутів – рівні сторони.
1.8	У рівносторонньому трикутнику всі кути рівні (60°)
2.  Прямокутний трикутник
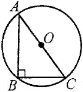
2.9	Трикутник називається прямокутним, якщо один із його кутів прямий.	АВ – гіпотенуза  АС, ВС – катети
2.10	Сторона прямокутного трикутника, що лежить навпроти прямого кута, називається гіпотенузою, а сторони, які утворюють прямий кут – катетами.
2.11	Сума гострих кутів прямокутного трикутника дорівнює 90°.
2.12	Катет прямокутного трикутника, який лежить навпроти кута 30, дорівнює половині гіпотенузи
2.13	Ознака рівності прямокутних трикутників за двома катетами: якщо катети одного трикутника відповідно дорівнюють катетам другого трикутника, то такі трикутники рівні;
2.14	Ознака рівності прямокутних трикутників за катетом і гострим кутом: якщо катет і прилеглий гострий кут одного трикутника дорівнюють відповідно катету і прилеглому гострому куту другого трикутника, то такі трикутники рівні;
2.15	Ознака рівності прямокутних трикутників за гіпотенузою і гострим кутом: якщо гіпотенуза і прилеглий кут одного трикутника дорівнюють відповідно гіпотенузі і прилеглому куту другого трикутника, то такі трикутники рівні;
2.16	Ознака рівності прямокутних трикутників катетом і гіпотенузою: якщо катет і гіпотенуза одного трикутника дорівнюють відповідно катету і гіпотенузі другого трикутника, то такі трикутники рівні.
3. Нерівності трикутника
3.17	Теорема. У кожному трикутнику проти більшої сторони лежить більший кут, а проти більшого кута – більша сторона.
3.18	Теорема. Кожна сторона трикутника менша від суми двох інших сторін.	В      А                                С
3.19	Наслідок. Якщо точки А, В, С не лежать на одній прямій, то правильні нерівності (нерівності трикутника):

 

 

 

 

 

 

 

 

 

 

 

Уроки №2, 3

«Радісне серце лице веселить..…»

Приповістей 15:13

Фронтальне опрацювання матеріалу

 

Рівнобедрений трикутник, його властивості і ознаки

 

І. Робота над засвоєнням понять, термінів і правил

 

Завдання 1.

1. Повторити тези 1.1 – 1.8 блоку №4.
2. Усно відповісти на питання:

1. Що називають трикутником?
2. Чому дорівнює периметр трикутника?
3. Що називають медіаною трикутника?
4. Що називають бісектрисою трикутника?
5. Що називають висотою трикутника?
6. Який трикутник називається рівнобедреним?
7. Сформулюйте властивість і ознаку рівнобедреного трикутника.
8. Що називається бічними сторонами і основою у рівнобедреному трикутнику?
9. Який трикутник називається рівностороннім, яка його властивість?

 

Завдання 2.

2.1. Усно розв’яжіть задачу

Казка-питання.

Зібралися представники всіх видів трикутників на лісовій галявині і стали обговорювати питання про вибір свого короля. Довго сперечалися і ніяк не могли прийти до єдиної думки. І ось один старий трикутник сказав: “ Давайте всі підемо до царства трикутників. Хто першим прийде, той і буде королем ”.

Всі погодилися. Рано вранці трикутники відправилися в далеку подорож. На дорозі мандрівників зустрілася річка, яка сказала: “ Перепливуть мене лише ті, у кого всі кути гострі ”.

Частина трикутників залишилися на березі, інші перепливли і відправилися далі. На дорозі їм зустрілася висока гора, яка сказала, що дасть пройти лише тим, у кого хоча б дві сторони рівні. Ті, що здолали другу перешкоду продовжили дорогу. Дійшли до великого урвища, де був вузький міст. Міст сказав, що пропустить тих, у кого всі сторони рівні. По мосту пройшов лише один трикутник, який першим дістався до царства і був проголошений королем.

Питання: 

Хто став королем?

Хто був основним суперником?

Хто першим вийшов із змагання?

 

2.2. Виконати усні вправи, запропоновані вчителем у презентації.

 

ІІ. Відпрацювання практичних умінь та навичок

Завдання 3.

Продовжте розв’язання кожної задачі

 

1. Накресліть трикутник АВС з тупим кутом В і проведіть висоту АН, бісектрису ВМ і медіану СК. Яка з точок Н, М і К лежить між двома іншими?

А

 

      В                      С    

2. Периметр рівнобедреного трикутника дорівнює 63 см. Бічна сторона в 1,5 рази менша, ніж основа. Знайдіть сторони цього трикутника.

Малюнок малювати не потрібно.

Короткий запис задачі:

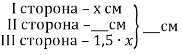
Завдання 4.

1.  Розв’язати задачу, запропоновану вчителем у презентації.
2. У рівнобедреному трикутнику АВС точка М лежить на середині сторони АС, 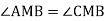. Знайдіть довжини відрізків ВС і СМ, якщо АВ=12 см, АС=8см.
3. Трикутники АВС і ADC рівносторонні. Відрізки BD і АС перетинаються в точці О. Доведіть, що АО=СО і .
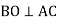4.                     Відрізок ВD є висотою рівнобедреного трикутника АВС (АВ = ВС), 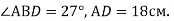Знайти кути DBC, ABC і основу АС.
5.                     У рівнобедреному трикутнику АВС з основою АС кут при основі на 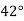менший від кута при вершині, протилежній основі. Знайдіть усі кути цього трикутника.

 

Готуємось до індивідуального опрацювання матеріалу

1. Накресліть трикутник АВС з прямим кутом С і проведіть висоту СН, бісектрису АК і медіану ВМ. Позначте на малюнку рівні відрізки і рівні кути.
2. Периметр рівнобедреного трикутника АВС дорівнює 72см, а бічна сторона  - 24см. Знайдіть інші сторони цього трикутника.
3. Основа рівнобедреного трикутника на 3 см менша за бічну сторону, а його периметр дорівнює 24 см. Знайдіть сторони трикутника.
4. Відрізок ВD є висотою рівнобедреного трикутника АВС (АВ = ВС), 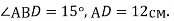                 Знайти кути DBC, ABC і основу АС.
5. У рівнобедреному трикутнику АВС з основою АС кут при основі на менший від кута при вершині, протилежній основі. Знайдіть усі кути цього трикутника.

 

Завдання на додатковий бал до ІОМ: (виконане завдання здати на уроці індивідуального опрацювання)

Вам випала нагода попрацювати дизайнерами і створити ескіз вітража, що складається із трикутників.

 

 

 

Уроки №5, 6

"Над усе, що лише стережеться,

серце своє стережи, бо з нього походить життя".

Приповістей 4:23

 

Фронтальне опрацювання матеріалу

 

Прямокутний трикутник. Ознаки рівності прямокутного трикутника

 

І. Робота над засвоєнням понять, термінів і правил

 

Завдання 1.

1. Повторити тези 2.9 – 2.16 блоку № 4.
2. Усно відповісти на питання:

1. Який трикутник називається прямокутним?
2. Як називаються сторони прямокутного трикутника?
3. Яка властивість гострих кутів прямокутного трикутника?
4. Сформулюйте ознаку рівності прямокутного трикутника за гіпотенузою і катетом.
5. Сформулюйте ознаку рівності прямокутного трикутника за двома катетами.
6. Сформулюйте ознаку рівності прямокутного трикутника за гіпотенузою і гострим кутом.
7. Сформулюйте ознаку рівності прямокутного трикутника за катетом і гострим кутом.
8. Сформулюйте властивість катета, який лежить навпроти кута 30.

 

Завдання 2.

Усно виконати вправи зі ст. 111:

465, 466.

 

ІІ. Відпрацювання практичних умінь та навичок

Завдання 3.

Письмово виконати вправи:

3.1. Знайдіть гострі кути прямокутного трикутника, якщо один з них на 12⁰ більший від другого.

3.2. У трикутнику АВС . Знайти АВ.

3. У прямокутному трикутнику MNK MN = NK, а гіпотенуза МК дорівнює 18см. Знайти довжину висоти, проведеної до гіпотенузи.

 

Завдання 4.

4.1. Усно виконати вправи, запропоновані вчителем у презентації.

4.2. Вам необхідно поділитись на групи по двоє людей.

Кожній парі  дається по 5 питань. Учні обмірковують відповіді протягом 3 хвилин, потім читають питання вголос і відповідають на них. Члени інших пар доповнюють і уточнюють відповіді

 

 

 

Команда 1

1. У трикутниках ABC і A_lB₁C_l   ∠C = C₁=90°; ∠A = ∠A₁. Доповніть умову задачі ще однією рівністю так, щоб рівність даних трикутників можна було довести за катетом й прилеглим гострим кутом. (АС = А₁С₁)

2. Чи існує рівнобедрений трикутник з бічною стороною 15 см і висотою, проведеною до основи 16см? (Ні.)

3. У прямокутному трикутнику ABC (∠C = 90°) ∠A=60°, AB = 10 см . Чому дорівнює катет AC? (5 см )

4. Чому дорівнюють гострі кути в прямокутному рівнобедреному  трикутнику?(По 45°)

5. Визначте вид трикутника, якщо відомо, що один із його зо­внішніх кутів дорівнює 90°. (Прямокутний)

 

Команда 2

1. У трикутниках ABC і A₁B₁C₁, ∠C = ∠C₁ =90° , ∠A = ∠A₁. Допо­вніть умову задачі ще однією рівністю так, щоб рівність даних трикутників можна було довести за гіпотенузою і гострим ку­том. (АВ = А₁В₁)
2. Чи існує рівнобедрений трикутник з бічною стороною 9 см і основою 18 см? (Ні)
3. У прямокутному трикутнику АСВ (∠C = 90°),  АВ = 20 см, ВС = 10 см. Знайдіть гострі кути трикутника. (30° і 60°)
4. Один із гострих кутів прямокутного трикутника дорівнює 50°. Знайдіть градусну міру іншого гострого кута. (40°)

5.  Гіпотенуза прямокутного трикутника дорівнює 10 см. Чому дорівнює медіана, проведена до неї? (5 см)      

 

4.3. Знайдіть кути прямокутного трикутника, якщо його висота, проведена з вершини прямого кута, утворює з катетом кут 50°

 

4.4. Знайти:  ВD, якщо КВ = 5 см.  Довести: рівність трикутників АКС і DКВ.

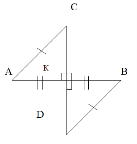
Завдання 5.

Для кращого засвоєння інформації, пройдіть тестування, зашифроване у QR- коді.

 

 

 

 

 

 

Готуємось до індивідуального опрацювання матеріалу

1. Гострі кути прямокутного трикутника відносяться як 3:7. Знайти ці кути.
2. У прямокутному трикутнику 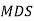катет 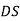дорівнює 28 см, 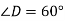. Знайти гіпотенузу .
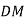3. На малюнку 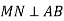, 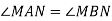. Доведіть, що .
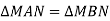4. Периметр трикутника дорівнює 22 см. Чи може одна з його сторін дорівнювати: 1) 12см; 2) 11см; 3) 10 см.
5. У прямокутному трикутнику градусні міри гострих кутів відносяться як 1:2, а різниця гіпотенузи і меншого катета дорівнює 9 см. Знайдіть гіпотенузу трикутника.

 

 

 

Урок №8

«Серце радісне добре лікує ...»

Приповістей 17:22

 

Внутрішньопредметне узагальнення матеріалу                      

 

Рівнобедрений трикутник. Прямокутний трикутник

 

І. Засвоєння термінології до теми

 

Завдання 1.

1. Повторити блок № 4.
2. Письмово дати відповідь на питання, запропоновані вчителем.

 

ІІ. Узагальнення практичних умінь та навичок

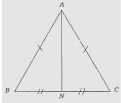
Завдання 2.

Усно виконати вправи:

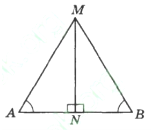
1. На малюнку AN – висота рівнобедреного трикутника АВС                                                                 з основою BC. Чому дорівнює BN, якщо BC = 6см?                         

 

А	Б	В	Г
3см	6см	12см	Визначити неможливо

2. Якщо в трикутнику MNK висота NL є його бісектрисою, то виконується рівність…

 

А	Б	В	Г
MK = NK	MN = NK	MK = MN	LK = MN

 

 

 

 

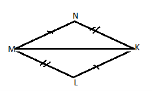
3. За якими елементами рівні трикутники, зображені на малюнку?

 

 

А	Б	В	Г
За двома сторонами і кутом між ними	За стороною та двома прилеглими кутами	За трьома кутами	За трьома сторонами

Завдання 3.

Письмово виконати вправи:

1. Периметр рівнобедреного трикутника дорівнює 24см, а бічна сторона – 10см. Знайти основу трикутника.
2. Один з гострих кутів прямокутного трикутника дорівнює 64°. Знайти другий гострий кут.
3. У рівнобедреному трикутнику АВС з основою АС кут при вершині на 24° більший від кута при основі. Знайдіть кути цього трикутника.
4. У прямокутному трикутнику АВС гіпотенуза АВ дорівнює 21см, а 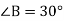. Знайти катет ВС.
5. Периметр рівнобедреного трикутника дорівнює 40см. На його бічній стороні побудували рівносторонній трикутник, периметр якого дорівнює 30см. Знайти основу рівнобедреного трикутника.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тема №5. Коло і круг

Урок №1

Коло і круг

«Господь стерегтиме тебе від усякого зла,

стерегтиме Він душу твою»

Псалом 121:7

Питання

1. Коло і круг.
2. Коло і трикутник.
3. Задачі на побудову

Література

Істер О.С. Геометрія: підручник для 7 класу загальноосвітніх навчальних закладів – К.: Генеза, 2015 рік, розділ 4, § 21 – 25, § 27 стор. 127 – 148; 155 – 168.

1.Коло і круг
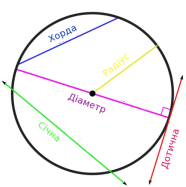
1.1	Коло – це геометрична фігура, що складається з усіх точок площини, рівновіддалених від даної точки. Дану точку називають центром кола.
1.2	Відрізок, що сполучає будь – яку точку кола з його центром, називають радіусом кола.
1.3	Відрізок, що сполучає дві довільні точки кола, називають хордою.
1.4	Хорда, що проходить через центр кола, називається діаметром.
1.5	Пряма, що має з колом дві спільні точки, називається січною.
1.6	Пряма, що має з колом одну спільну точку, називається дотичною до кола.
1.7	Дотична до кола перпендикулярна до його радіуса, проведеного у точку дотику.
1.8	Відрізки дотичних, проведених з однієї точки до кола, рівні між собою.
1.9	Якщо два різні кола мають дві спільні точки, то говорять, що вони перетинаються в цих точках.
1.10	Якщо два кола мають тільки одну спільну точку, говорять, що вони дотикаються в цій точці.	Внутрішній  Зовнішній дотик дотик
1.11	Два кола, які мають один центр, називаються концентричними.
1.12	Об’єднання кола з його внутрішньою частиною називають кругом.
1.13	– довжина кола   - площа круга
2. Коло і трикутник
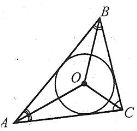
2.14	Коло називається вписаним у трикутник, якщо воно дотикається до всіх сторін трикутника.
2.15	Теорема. У кожний трикутник можна вписати лише одне коло. Його центром є точка перетину двох бісектрис трикутника.
2.16	Коло називається описаним навколо трикутника, якщо воно проходить через усі вершини трикутника.
2.17	Теорема. Навколо кожного трикутника можна описати лише одне коло. Його центром є точка перетину серединних перпендикулярів двох сторін трикутника (прямі, що проходять через середину відрізка, перпендикулярно до нього)
2.18	Наслідок. Центром кола, описаного навколо прямокутного трикутника, є середина його гіпотенузи.
3. Задачі на побудову
3.19	Основні види задач на побудову: Побудова кута, що дорівнює даному; Побудова бісектриси даного кута; Поділ даного відрізка навпіл; Побудова прямої перпендикулярної до даної; Побудова трикутника за трьома сторонами.

Урок №2

«Учітесь, читайте, і чужому научайтесь,

 і свого не цуpайтесь…»

Т. Шевченко

 

Фронтальне опрацювання матеріалу

 

Коло і круг. Взаємне розташування двох кіл

 

І. Робота над засвоєнням понять, термінів і правил

 

Завдання 1.

1. Повторити тези 1.1 – 1.13 блоку № 5.
2. Усно відповісти на питання:

1. Що називають колом?
2. Які елементи кола вам відомі? Дайте визначення кожному з них.
3. Які розташування двох кіл вам відомі?
4. Що називають кругом?
5. Як пов’язані між собою діаметр і радіус кола?
6. Записати на дошці формули довжини кола і площі круга.

 

Завдання 2.

2.1. Виконати усно вправу 577 ст. 130.

2.          Обчисліть радіус кола, якщо його діаметр дорівнює:

1. 4 см;
2. 7,8 см.
   3.          Обчисліть діаметр кола, якщо його радіус дорівнює:

1. 2 см;
2. 4,9 см.

 

ІІ. Відпрацювання практичних умінь та навичок

Завдання 3.

Письмово виконати вправи:

1. Практична робота. Накресліть коло з центром у точці О і радіусом 2см. Проведіть у даному колі радіус, діаметр і хорду, що не є діаметром.
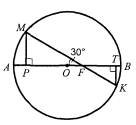2. Хорда кола МК перетинає його діаметр АВ у точці F, 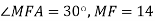см, 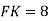см. Знайдіть довжини відрізків МР і КТ.
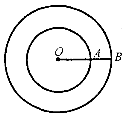3. Два кола мають спільний центр О. Їх радіуси відносяться як

9:5, а АВ=8см. Визначте радіуси кіл.

 

 

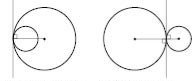
4. Радіуси двох кіл дорівнюють 6 см і 9 см. Знайдіть відстань між їх центрами, якщо кола мають: 1) внутрішній дотик; 2) зовнішній дотик.
5. Перед посівом соняшників у підприємців виникло питання щодо вибору найбільш врожайного сорту. Один з багатьох запропонованих сортів дає можливість виростити соняшники діаметром 30 см (у середньому), а другий — соняшники діаметром 20 см (у середньому). При цьому чисельність на 1 га рослин першого сорту вдвічі менша від чисельності на 1 га рослин другого сорту. Який сорт соняшнику вибрали підприємці?

Розв’язання. Нехай чисельність соняшників першого сорту дорівнює m штук на 1 га, тоді чисельність соняшників другого сорту дорівнює 2m штук на 1 га. Тоді площа, яку мають корзинки соняшників першого сорту, на 1 га дорівнює 706,5m см², а корзинки соняшників другого сорту — 628m см². Отже, підприємці вибрали перший сорт.

Відповідь. Перший сорт.

 

 

Урок №3

«Ну що здавалося б слова.

Слова та голос – більш нічого.

А серце б’ється – ожива, як їх почує!»

Т. Шевченко

 

Фронтальне опрацювання матеріалу

 

Дотична до кола

 

І. Робота над засвоєнням понять, термінів і правил

 

Завдання 1.

1. Повторіть тези 1.1 – 1.13 блоку №5.
2. Дайте відповіді на питання:

1. Що називають колом?
2. Які елементи кола вам відомі? Дайте визначення кожному з них.
3. Які розташування двох кіл вам відомі?
4. Що називають кругом?
5. Як пов’язані між собою діаметр і радіус кола?
6. Що називають дотичною до кола?
7. Яка властивість дотичної до кола?

Завдання 2.

Усно виконати вправи:

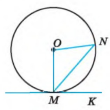
2.1. Назвати елементи кола зображеного на малюнку

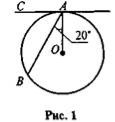
2. Дано: СА — дотична до кола. Знайдіть кут ВАС.

 

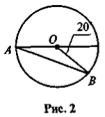
2.3. Знайдіть кути трикутни­ка АОВ.

 

 

2.4. Дано: СА — дотична до кола.

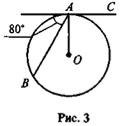
Знайдіть кут ВАО.

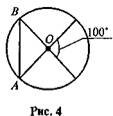
2.5. Знайдіть кути трикутника АОВ.

 

 

 

 

ІІ. Відпрацювання практичних умінь та навичок

Завдання 3.

Письмово виконати вправи:

3.1. Накресліть коло, радіус якого дорівнює 3 см. Позначте на ньому точку Р. За допомогою косинця проведіть через точку Р дотичну до цього кола.

3.2. Радіус кола дорівнює 8см. Як розміщені пряма і коло, якщо відстань від центра кола до цієї прямої дорівнює:

1) 5 см;   2) 8 см;   3) 9 см.

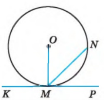
3.3. На малюнку КР – дотична до кола, точка О – центр кола. Знайдіть .

3.4. Пряма МК – дотична до кола, точка О – центр кола. Знайдіть .

ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних завдань і вправ

Завдання 4.

Виконайте тестування, яке знаходиться за посиланням http://cutt.us/0X2qu

 

 

 

Урок №4

«Усе, що робиш, треба робити добре»

Ф.Бекон

 

Фронтальне опрацювання матеріалу

 

Коло, вписане в трикутник

 

І. Робота над засвоєнням понять, термінів і правил

 

Завдання 1.

1. Повторіть тези 1.1 – 2.15 блоку №5.
2. Дайте відповіді на питання:

1. Що називають колом? Кругом?
2. Які елементи кола вам відомі? Дайте їм визначення.
3. Яке коло називається вписаним у трикутник.
4. Сформулюйте теорему про коло, вписане в трикутник.
5. Що називають дотичною?
6. Сформулюйте властивість дотичної.
7. Який взаємозв’язок між радіусом і діаметром кола?

Завдання 2.

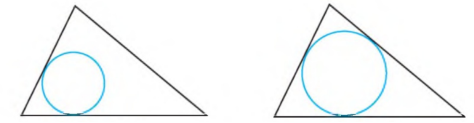
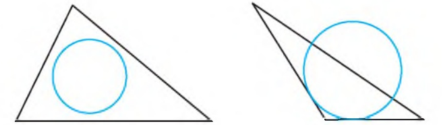
На якому з малюнків зображено коло, вписане в трикутник?

ІІ. Відпрацювання практичних умінь та навичок

Завдання 3.

Письмово виконати вправи:

3.1. Накресліть гострокутний трикутник. За допомогою транспортира, циркуля і лінійки побудуйте коло, вписане в даний трикутник.

2. Три заводи розміщені у вершинах А, В і С різностороннього трикутника і сполучені між собою магістралями. Всередині цього трикутника на однаковій відстані від магістралей розташований населений пункт О, який сполучено дорогами з кожним заводом. Яким має бути найкоротший замкнений маршрут автобуса, призначеного для розвезення жителів населеного пункту до всіх трьох заводів?

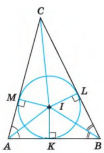
3.3. У вписано коло з центром у точці . Знайдіть кути трикутника , якщо .

3.4. Коло, вписане в рівнобедрений трикутник, ділить його бічну сторону на відрізки 3 см і 4 см, починаючи від основи. Знайдіть периметр трикутника.

 

 

Урок №5

«Математика вчить мислити й разом з тим

вселяє віру в безмежні сили людського розуму»

В. О. Сухомлинський

 

Фронтальне опрацювання матеріалу

 

Коло, описане навколо трикутника

 

І. Робота над засвоєнням понять, термінів і правил

 

Завдання 1.

1. Повторіть тези 1.1 – 2.18 блоку №5.
2. Дайте відповіді на питання:

1. Що називають серединним перпендикуляром?
2. Яке коло називають описаним навколо трикутника?
3. Де знаходиться центр кола, описаного навколо трикутника?
4. Де знаходиться центр кола, описаного навколо прямокутного трикутника?
5. Де знаходиться центр кола, вписаного в трикутник?
6. Яке коло називають вписаним у трикутник?
7. Дайте означення дотичної до кола?
8. Скільки спільних точок має дотична з колом?
9. Як розміщена дотична до радіуса кола, проведеного в точку дотику?

 

Завдання 2.

1. На якому з малюнків пряма є серединним перпендикуляром до відрізка ?

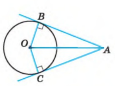
2. На якому з малюнків зображено коло, описане навколо трикутника?

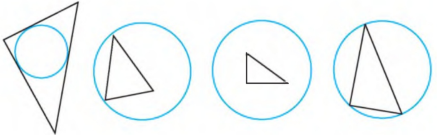
3. Накресліть відрізок 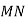, який дорівнює 5,6 см. За допомогою лінійки з поділками і косинця проведіть серединний перпендикуляр до відрізка 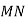. Позначте деяку точку 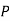, що належить серединному перпендикуляру, і переконайтеся, що .

 

 

ІІ. Відпрацювання практичних умінь та навичок

Завдання 3.

Письмово виконати вправи:

3.1. Накресліть гострокутний трикутник. За допомогою креслярських інструментів опишіть навколо нього коло.

3.2. Знайдіть кут , якщо кут .

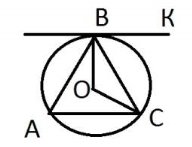
3.3. Три кола попарно ззовні дотикаються одне до одного. Відрізки, що сполучають їх центри, утворюють трикутник зі сторонами 9 см, 10 см і 11 см. Визначте радіуси кіл.

 

ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач і вправ

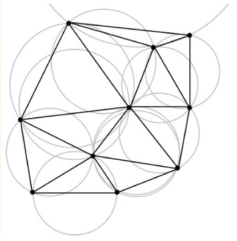Кожному, хто бажає отримати додаткові 2 бали до індивідуального опрацювання матеріалу, виконати наступні завдання:

1.                Вказати коло і відповідний трикутник, вписаний у нього.
2.                Завдання виконати кольоровими олівцями.

 

 

 

 

 

 

 

 

 

 

Урок №6

«Те, що не може геометрія, не можемо й ми»

Блез Паскаль

 

Фронтальне опрацювання матеріалу

 

Задачі на побудову

 

І. Робота над засвоєнням понять, термінів і правил

 

Завдання 1.

1. Повторіть тези блоку №5.
2. Дайте відповіді на питання:

1. Які види задач на побудову вам відомі?
2. Що називають трикутником?
3. Що називають колом і кругом?
4. Назвіть елементи кола.
5. Що називають дотичною?
6. Які кола називають концентрованими?
7. Де лежить центр кола, описаного навколо прямокутного трикутника?
8. Що називають кутом?
9. Що називають бісектрисою кута?

 

Завдання 2.

2.1. Переглянути презентацію, запропоновану вчителем.

2.2. Записати алгоритми побудови основних задач, поданих у презентації.

 

ІІ. Відпрацювання практичних умінь і навичок

 

Завдання 3.

Клас ділиться на групи 5 груп. Кожна група виконує відповідне завдання.

 

Група 1.

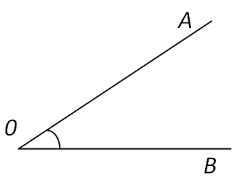
Побудувати бісектрису для даного кута.

 

Група 2.

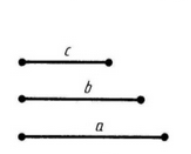
Побудувати трикутник за даними сторонами.

 

 

Група 3.

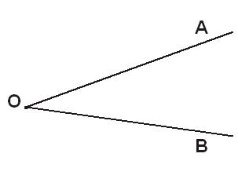
Побудувати кут, рівний даному.

 

 

Група 4.

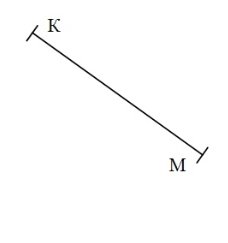
Поділити даний відрізок навпіл.

 

Група 5.

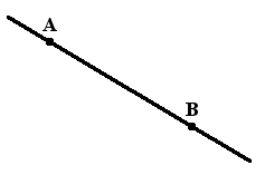
Побудувати пряму, перпендикулярну до даної

 

Готуємось до індивідуального опрацювання матеріалу

1. Накресліть коло радіуса 21 мм. Проведіть в ньому діаметр 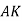та хорду 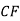. Проведіть за допомогою косинця дотичну до кола, що проходить через точку А.
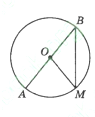2. На малюнку точка О – центр кола, 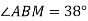. Знайдіть .
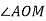3. Відстань між центрами двох кіл дорівнює 6 см. Визначте взаємне розміщення цих кіл, якщо їх радіуси дорівнюють: 1) 8 см і 2 см;  2) 5 см і 3 см;  3) 2 см і 3 см.
4. Дано пряма 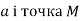. Побудуйте пряму, перпендикулярну до прямої 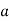, яка проходить через точку  .

 

 

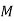Урок №8

«Не дивіться на Україну, як на землю своїх батьків.

Дивіться на неї, як на землю своїх дітей.

І тоді прийдуть зміни»

Святослав Вакарчук

 

Внутрішньопредметне узагальнення матеріалу                      

 

Коло і круг

 

І. Засвоєння термінології до теми

 

Завдання 1.

1. Повторити блок № 5.
2. Письмово дати відповідь на питання, запропоновані вчителем.

 

ІІ. Узагальнення практичних умінь та навичок

 

Завдання 2.

Усно виконати вправи:

1. Знайдіть діаметр кола, радіус якого дорівнює 6 см.                          

 

А	Б	В	Г
24 см	3 см	12см	см

 

2. Укажіть малюнок, у якому пряма є січною до кола.

 

 

 

 

3. На якому з малюнків зображено коло, описане навколо трикутника.

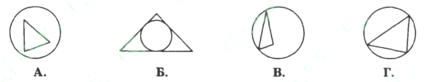
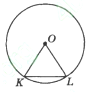Завдання 3.

Письмово виконати вправи:

4. Точка О – центр кола, - його хорда. Знайдіть градусну міру кута , якщо .
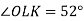5. Кола, радіуси яких дорівнюють 5 см і 3 см, мають зовнішній дотик. Знайдіть відстані між центрами цих кіл.
6. У колі з центром О проведено хорду АВ і діаметр ВС. Знайдіть кути трикутника АОВ, якщо .
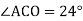7. Два кола мають внутрішній дотик. Радіус одного з них у 4 рази більший за радіус другого. Знайдіть радіуси кіл, якщо відстань між їх центрами дорівнює 21 см.
8. Коло, вписане в рівнобедрений трикутник, ділить його бічну сторону на відрізки 7 см і 5 см, починаючи від вершини, що лежить проти основи. Знайдіть периметр трикутника.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тема №6. Повторення матеріалу, вивченого у           7 класі

Урок №1

«Для вченої й освіченої людини жити – значить мислити»

Цицерон

 

Внутрішньопредметне узагальнення матеріалу за рік                      

 

Паралельність прямих. Сума кутів трикутника

 

І. Засвоєння термінології до теми

 

Завдання 1.

Дайте відповіді на питання:

1. Які прямі називаються паралельними?
2. Які кути утворюються при перетині двох прямих січною?
3. Сформулюйте властивості паралельних прямих.
4. Сформулюйте ознаки паралельності прямих.
5. Чому дорівнює сума кутів трикутника?
6. Що називають зовнішнім кутом трикутника?
7. Яка властивість зовнішнього кута трикутника?

 

ІІ. Узагальнення практичних умінь та навичок

 

Завдання 2.

Усно виконати вправи:

1. Знайдіть третій кут трикутника, якщо два з його кутів дорівнюють .

 

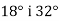А	Б	В	Г

 

2. За даним малюнком укажіть, як називаються кути 1 і 2.

 

А	Б	В	Г
Внутрішні різносторонні	Внутрішні односторонні	Відповідні	Вертикальні

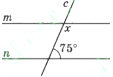
3. На малюнку прямі паралельні, 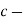січна. Знайдіть градусну міру кута .

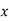А	Б	В	Г

 

 

 

Завдання 3.

Письмово виконати вправи:

1. Один із восьми кутів, що утворились при перетині паралельних прямих січною, дорівнює 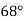. Знайдіть решту кутів.
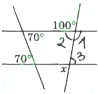2. У результаті перетину двох прямих січною утворились внутрішні односторонні кути, один з яких дорівнює 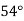, а другий – на 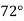більший. Визначте взаємне розміщення цих прямих.
3. Знайдіть зовнішні кути трикутника, якщо його внутрішні кути відносяться як 18:11:7.
4. За даним малюнком знайдіть градусну міру кута .
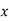5. Знайдіть кути рівнобедреного трикутника, якщо кут при вершині на 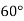менший за кут при основі.

 

 

 

Урок №2

«Якщо запастися терпінням і проявити старання,

то посіяне насіння знання неодмінно дасть добрі плоди»

Леонардо да Вінчі

 

Внутрішньопредметне узагальнення матеріалу за рік                      

 

Трикутник. Ознаки рівності трикутників

 

І. Засвоєння термінології до теми

 

Завдання 1.

Дайте відповіді на питання:

1. Що називають трикутником?
2. Сформулюйте три ознаки рівності трикутників.
3. Що називають висотою, медіаною і бісектрисою трикутника?
4. Які фігури називаються рівними?
5. Які види трикутників за кутами вам відомі?
6. Які трикутники називаються рівними?

 

ІІ. Узагальнення практичних умінь та навичок

 

Завдання 2.

Усно виконати вправи:

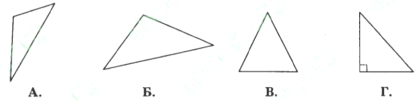
1. Укажіть, який з трикутників є прямокутний.

                                                                                                                                           

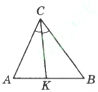
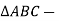2. різносторонній, 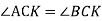. Як називають відрізок ?

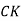А	Б	В	Г
Сторона трикутника	Висота трикутника	Бісектриса трикутника	Медіана трикутника

 

 

3. Про трикутники відомо, що 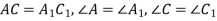. Тоді…

А	Б	В	Г
за першою ознакою	за другою ознакою	за третьою ознакою	Рівність трикутників встановити неможливо

 

Завдання 3.

Письмово виконати вправи:

1. Накресліть гострокутний трикутник . За допомогою лінійки з поділками проведіть у ньому медіану .
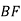2. Знайдіть сторони трикуника, якщо вони пропорційні числам 4, 5 і 6, а периметр трикутника дорівнює 60см.
3. Доведіть рівність трикутників .
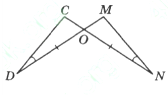
4. У рівнобедреному трикутнику з основою проведено медіану . Знайдіть периметр трикутника 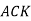, якщо периметр трикутника 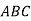дорівнює 18 см, а .

 

 

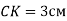Урок №3

«Алгебра і геометрія – єдині країни, де панують тиша і мир»

Марія Ананьєзі

 

Внутрішньопредметне узагальнення матеріалу за рік                      

 

Трикутник. Ознаки рівності трикутників

 

І. Засвоєння термінології до теми

Завдання 1.

Дайте відповіді на питання:

1. Яка наука називається геометрією?
2. Назвіть основні геометричні фігури.
3. Які фігури називаються плоскими?
4. Сформулюйте властивість суміжних і вертикальних кутів.
5. Які прямі називаються паралельними? Перпендикулярними?
6. Сформулюйте ознаки паралельності прямих.
7. Що називають трикутником?
8. Який трикутник називається рівнобедреним? Рівностороннім? Прямокутним?
9. Сформулюйте ознаки рівності трикутників.
10. Сформулюйте ознаки рівності прямокутних трикутників.
11. Сформулюйте властивість рівнобедреного трикутника.
12. Що називають колом? Кругом?
13. Дайте визначення основним елементам кола.

 

ІІ. Узагальнення практичних умінь та навичок

Завдання 2.

Усно виконати вправи:

1. Знайдіть кут, якщо його бісектриса утворює з його стороною кут, який дорівнює 20°.

 

А	Б	В	Г
10°	40°	60°	120°

 

2. Три точки А, В, С лежать на одній прямій. Яка з точок А, В, С лежить між двома іншими, якщо АВ = 4 см, ВС = 3 см, АС = 7 см?

 

А	Б	В	Г
А між В і С	В між А і С	С між А і В	Визначити неможливо

 

3. Кут при основі рівнобедреного трикутника дорівнює 15°. Знайдіть кут при вершині цього трикутника.

 

А	Б	В	Г
30°	165°	150°	70°

 

Завдання 3.

Письмово виконати вправи:

1. Один із кутів, що утворилися при перетині двох прямих, дорівнює 163°. Знайдіть решту кутів.
2. Знайдіть кути трикутника, якщо один з них дорівнює 40°, градусні міри двох інших  відносяться як 2 : 5 .
3. Периметр рівнобедреного трикутника дорівнює 54 см. Його основа менша від бічної сторони на 8 см. Знайти сторони цього трикутника.
4. Знайдіть гострі кути прямокутного трикутника, якщо його зовнішні кути при тих самих вершинах відносяться як 7:11.

 

 

 

Готуємось до індивідуального опрацювання матеріалу

1. Один із кутів, що утворились при перетині двох прямих, дорівнює 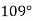. Знайдіть решту кутів.
2. Периметр рівнобедреного трикутника дорівнює 22см, а його бічна сторона – 7 см. Знайдіть основу трикутника.
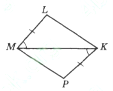
3. Дано: . Доведіть, що .
4. Один із кутів трикутника дорівнює 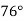, а другий на 12 більший за третій. Знайдіть невідомі кути трикутника.
5. Знайдіть гострі кути прямокутного трикутника, якщо його зовнішні кути при тих самих вершинах відносяться як 17:13.

 

 

Урок №5

«Коли двоє роблять одне і те ж, це не означає,

 що у них вийде одне й те саме»
Автор не відомий

 

Внутрішньопредметне узагальнення за рік

 

І. Узагальнення практичних умінь і навичок

 

Завдання 1.

 

1. Знайдіть кут, якщо його бісектриса утворює з його стороною кут, який дорівнює 20°.

 

А	Б	В	Г
10°	40°	60°	120°

 

2. Три точки А, В, С лежать на одній прямій. Яка з точок А, В, С лежить між двома іншими, якщо АВ = 4 см, ВС = 3 см, АС = 7 см?

 

А	Б	В	Г
А між В і С	В між А і С	С між А і В	Визначити неможливо

 

3. Кут при основі рівнобедреного трикутника дорівнює 15°. Знайдіть кут при вершині цього трикутника.

 

А	Б	В	Г
30°	165°	150°	70°

 

 

 

 

ІІ. Письмове виконання вправ

 

Завдання 2.

1. Знайдіть кути трикутника, якщо один з них дорівнює 54°,  а другий на 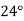менший від третього.
2. Периметр рівнобедреного трикутника дорівнює 24 см. Його основа менша від бічної сторони на 6 см. Знайти сторони цього трикутника.
3. Відрізок висота рівнобедреного трикутника 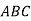з основою ВС, зображеного на рисунку. Яка градусна міра кута СВК?
4. Трикутник АВС вписаний у коло так, що сторону АВ видно з центра кола під кутом 120°, а сторону ВС під кутом 100°. Знайдіть кути трикутника АВС.

 

 

 

 

 

 

 

 

Урок №7

 

Творчий залік

Захист проектів «Все навколо – геометрія»

 

Клас ділиться на 4 групи відповідно до побажань і нахилів учнів. Кожній групі необхідно виконати певне завдання і на уроці захистити виконану роботу у заданій формі.

 

1 група

Вам необхідно виконати проект, використавши метод «storytelling» - розкриття основних понять через розповідь або складання казки. Вам потрібно скласти казку про ті геометричні фігури, які ми вивчали протягом року у 7 класі, наприклад «Якими б фігурами могли бути трикутник і коло?». У казці повинні бути розкриті основні властивості та означення цих фігур. На уроці-захисті вам необхідно казку озвучити, використавши ілюстрації.

Приклад методу можна побачити у книзі Лева Генденштейна «Аліса в країні математики»

 

2 група

Вашим завданням буде створити мозаїку із відомих геометричних фігур, використовуючи метод «Танграм», і розповісти про фігури які використали. Використайте різні засоби: папір, фетр, картон різних видів і т.п. Вам необхідно зробити хоча б 3 мозаїки. На уроці-захисті про кожну з них необхідно буде розповісти.

Приклад:

 

3 група

Вам необхідно створити малюнки, використавши прийом «Піктограма» або «наскельний малюнок». Піктограма (від лат. pictus — мальований і грец. γράμμα — письмовий знак, риска, лінія) – умовний малюнок із зображенням будь-яких дій, явищ, предметів тощо. Піктограми беруть початок із давніх часів, коли вони використовувалися для передавання будь-яких відомостей. Саме спосіб піктограм ліг в основу формування писемності. Кожному учаснику групи потрібно створити свій наскельний малюнок, в основу якого покласти якийсь термін чи поняття, вивчені на уроках геометрії у 7 класі. Всі пікторами мають бути зашифровані, а на уроці-захисті ваша група продемонструє їх, і однокласники мають розшифрувати захований зміст.

Приклад:

 

4 група

Ваше завдання – дуже оригінальне. Вам необхідно створити закладки у книги, використавши елементи геометричних фігур, відомих вам з уроків геометрії. Види закладок, які повинні бути створені: закладки-кутики, закладки-орігамі, закладки-плетіння, закладки з паличок для морозива, закладки-малюнки. Кожний учасник групи повинен створити кожний вид закладок. Приклади та ідеї, а також техніку створення ви можете знайти за посиланням: https://utka.su/AmbOG або в QR-коді