Навчальний посібник "Геометрія 9 клас І семестр"
Посібник розроблений згідно Комбінованої системи М.П. Гузика і може бути використаний як додатковий матеріал для учнів на уроки. Кожна тема посібника має таку структуру:
- перший урок – урок розбору блоку навчальної інформації;
- наступні уроки – уроки фронтального опрацювання матеріалу,
- між уроками фронтального опрацювання містяться завдання по підготовці до уроків індивідуального опрацювання матеріалу;
- в кінці кожної теми є один урок внутрішньопредметного узагальнення матеріалу, на якому кожен продемонструє свої знання блоку, а також узагальнить знання і вміння, здобуті під час теми.
Ківерцівська експериментальна школа
Навчальний посібник


І семестр

Шановні учні!!!
В цьому навчальному році ви продовжите вивчати геометрію, а допоможе вам у цьому посібник, який ви тримаєте в руках.
Він містить уроки розбору блоку навчального матеріалу, уроки фронтального опрацювання матеріалу та уроки внутрішньопредметного узагальнення матеріалу.
 Перевірити свої знання і підготуватись до індивідуального опрацювання матеріалу можна, виконавши завдання у рубриці «Готуємось до індивідуального опрацювання матеріалу», позначеного
Перевірити свої знання і підготуватись до індивідуального опрацювання матеріалу можна, виконавши завдання у рубриці «Готуємось до індивідуального опрацювання матеріалу», позначеного
Якщо ви пропустите один або кілька уроків, опрацюйте матеріал цих уроків вдома.
Бажаю успіхів у вивченні геометрії!!!
Блок №1. Координати на площині
Урок №1

Координати на площині
«Велика справа Декарта – створення аналітичної
геометрії – перекинула міст між алгеброю і геометрією»
С.І. Вавилов, вчений-генетик, ботанік
Питання
- Координатна площина.
- Координати середини відрізка. Відстань між двома точками із заданими координатами.
- Поняття рівняння фігури. Рівняння кола.
- Рівняння прямої.
Література
Істер О.С. Геометрія: Підручник для 9 класу, §1, 3 – 5, стор. 6 – 11, 21 – 53.
|
1. Координатна площина |
||
|
1.1 |
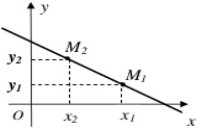
Проведемо дві перпендикулярні координатні прямі, які перетинаються у точці О – їх спільному початку відліку. Ці прямі називаються осями координат, О – початком координат. Горизонтальну вісь називають віссю абсцис і позначають буквою х, вертикальну – віссю ординат і позначають буквою у. Вісь абсцис і вісь ординат утворюють прямокутну систему координат на площині. |
|
|
1.2 |
Площину із введеною на ній системою координат називають координатною площиною. |
|
|
1.3 |
Впорядкована пара чисел, яка відповідає кожній точці координатної площини, називається координатами точки. А (х; у); х – абсциса точки; у – ордината точки В (х; 0) – точка, що лежить на осі абсцис С (0; у) – точка, що лежить на осі ординат
|
|
|
2. Координати середини відрізка. Відстань між двома точками із заданими координатами. |
||
|
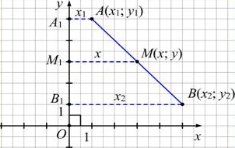
2.4 |
Теорема 1 (про координати середини відрізка) Кожна координата середини відрізка дорівнює півсумі відповідних координат його кінців:
|
|
|
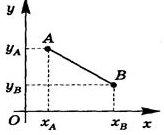
2.5 |
Теорема 2 (про відстань між двома точками із заданими координатами) Відстань між двома точками дорівнює кореню квадратному із суми квадратів різниць їх відповідних координат:
|
|
|
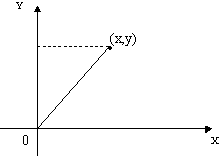
2.6 |
Наслідок з теореми 2 Відстань від точки до початку координат дорівнює кореню квадратному із суми квадратів її координат:
|
|
|
3. Поняття рівняння фігури. Рівняння кола |
||
|
3.7 |
Рівняння з двома змінними х і у називається рівнянням фігури, якщо виконуються дві умови: 1) координати будь-якої точки фігури задовольняють рівняння; 2) будь-які два числа, що задовольняють це рівняння, є координатами деякої точки фігури. |
|
|
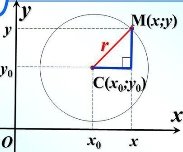
3.8 |
Теорема 3 (про рівняння кола)
Коло з центром
|
|
|
3.9 |
Наслідок з теореми 3
Якщо центр кола міститься у початку координат, то рівняння кола має вигляд: |
|
|
4. Рівняння прямої |
||
|
4.10 |
Рівняння прямої, що проходить через дві точки
Пряма, що проходить через дві точки
|
|
|
4.11 |
Загальне рівняння прямої
( |
|
|
4.12 |
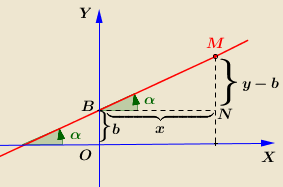
Рівняння прямої з кутовим коефіцієнтом
1) Пряма, що не проходить через початок координат, задається рівнянням
2) Пряма, що проходить через початок координат, задається рівнянням |
|
|
4.13 |
Кутовий коефіцієнт дорівнює тангенсу кута між даною прямою і додатною піввіссю Ох:
|
|
|
4.14 |
Умова паралельності прямих Якщо кутові коефіцієнти двох прямих рівні, то прямі паралельні, і навпаки. |
|
|
4.15 |
Умова перпендикулярності прямих Дві прямі взаємно перпендикулярні тоді і тільки тоді, коли добуток їх кутових коефіцієнтів дорівнює – 1. |
|
Урок №2
«Хороші друзі дістаються тому,
хто сам вміє бути справжнім другом»
Народна мудрість
Фронтальне опрацювання матеріалу
Координати середини відрізка. Відстань між двома точками
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 2.6 блоку № 1.
- Усно дай відповідь на питання:
- Що таке система координат?
- Що називають координатною площиною?
- Що називають координатами точки?
- Чому дорівнює відстань між двома точками із заданими координатами?
- Чому дорівнює відстань від точки до початку координат?
- Чому дорівнюють координати середини відрізка?
Завдання 2.
Усно виконай вправи:
- На якому з наведених рисунків зображена координатна пряма?
![]()
![]()
![]()
![]()
![]()
![]()
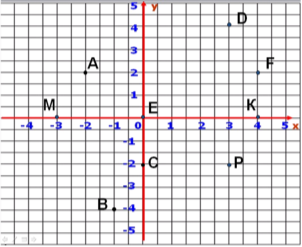
- Прочитай запис:
М (5;3); Р (-5; 0); О (0; 0).
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ, застосування правил
Завдання 3.
Усно виконай вправи:
- Визнач координати точок, зображених на малюнку:
- Чи правильно заповнена таблиця?
|
Координати точки |
(2;3) |
(-5;-1) |
(-4;6) |
(-3;5) |
|
Відстань до осі абсцис |
2 |
- 1 |
6 |
5 |
|
Відстань до осі ординат |
3 |
-5 |
4 |
3 |
Завдання 4.
Письмово виконай вправи, стор. 10, 26 – 27 підручника: 14; 75 (1); 85 (1); 88; 92.
Урок №3
«Доброта – це те, що може
почути глухий і побачити сліпий»
Народна мудрість
Фронтальне опрацювання матеріалу
Рівняння кола
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 3.9 блоку № 1.
- Дай відповіді на питання:
- Запиши формулу відстані між точками
- Запиши формулу знаходження середини відрізка
- Запиши рівняння кола
- Що потрібно мати, щоб скласти рівняння кола?
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 2.
- За рисунком склади рівняння кола з центром у точці К.
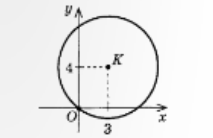
- Склади рівняння кола з центром у точці D.
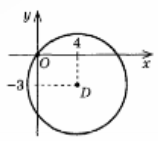
- Визнач координати центра і радіус кола, заданого рівнянням:
-
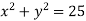 ;
;
-
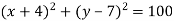 ;
;
-
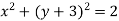 .
.
Завдання 3.
- Виконай вправу 126, стор. 32 підручника.
-
Дано точки А
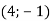 , М
, М 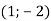 , причому точка М – середина відрізка АВ. Знайди координати точки В.
, причому точка М – середина відрізка АВ. Знайди координати точки В.
-
Склади рівняння кола, якщо О
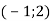 – центр кола, А
– центр кола, А 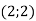 – точка кола.
– точка кола.
- Виконай вправу 136, стор. 33 підручника.
Урок №4
«Всі хочуть змінити світ,
але ніхто не хоче змінитися сам»
Л. М. Толстой
Фронтальне опрацювання матеріалу
Рівняння прямої
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори блок № 1.
- Усно дай відповідь на питання:
- Що називається рівнянням фігури, заданої на площині ХУ?
-
Який вид має рівняння кола с центром у точці
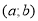 та радіусом
та радіусом 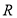 ?
?
-
Який вид має рівняння кола з центром в початку координат і радіусом
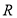 ?
?
- Запиши загальне рівняння прямої.
- Запиши рівняння прямої з кутовим коефіцієнтом.
- Запиши рівняння прямої, що проходить через дві точки.
- Назви умову, за якої прямі паралельні і перпендикулярні.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 2.
Усно виконай вправу:
Чому дорівнює кутовий коефіцієнт прямої:
-
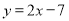 ;
;
-
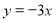 ;
;
-
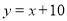 ;
;
-
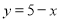 ;
;
-
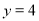 ;
;
-
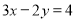 .
.
Завдання 3.
Письмово виконай вправи:
-
Склади рівняння прямої яка проходить через точки
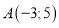 та
та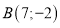 .
.
-
Склади рівняння прямої, що проходить через точки:
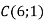 і
і 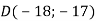 .
.
-
Склади рівняння прямої, яка проходить через точку
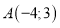 та паралельна прямій
та паралельна прямій 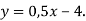
-
Склади рівняння прямої, яка містить медіану ВМ трикутника АВС, якщо А
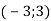 , В
, В 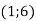 , С
, С 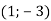 .
.
 Готуємось до індивідуального опрацювання матеріалу
Готуємось до індивідуального опрацювання матеріалу
- Знайди відстань від початку координат до точки А (5; 2).
-
Знайди координати центра кола, заданого рівнянням
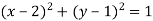 .
.
-
Дано точки К
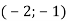 , N
, N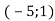 , причому точка К – середина відрізка MN. Знайди координати точки М.
, причому точка К – середина відрізка MN. Знайди координати точки М.
-
Склади рівняння кола, якщо О
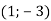 – центр кола, А
– центр кола, А 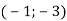 – точка кола.
– точка кола.
-
Склади рівняння прямої, яка містить середню лінію трикутника АВС, паралельну АС, якщо А
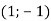 , В
, В 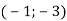 , С
, С 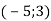 .
.
Урок №6
«О, коли б ми в ганебних справах були такі ж соромливі і боязкі,
як це часто ми буваємо боязкі і хибно соромливі у порядних вчинках!»
Григорій Сковорода
Внутрішньопредметне узагальнення матеріалу
Декартові координати на площині
І. Систематизація та узагальнення теоретичних знань
Завдання 1.
- Повтори блок № 1. Особливу увагу зверни на тези 1.2, 1.3, 1.4, 2.6, 3.8, 3.9, 4.10 – 4.15.
- Дай письмово відповідь на питання, запропоновані вчителем.
ІІ. Систематизація та узагальнення практичних умінь та навичок
Завдання 2.
Усно виконай вправи:
- Яка з наведених точок належить: 1) осі абсцис; 2) осі ординат?
|
А |
Б |
В |
Г |
|
|
|
|
|
- Знайди координати середини відрізка АВ, якщо А (– 4; 0); В (– 2; – 6).
|
А |
Б |
В |
Г |
|
|
|
|
|
- Знайди відстань між точками А (3; 1) і В (5; 2)
|
А |
Б |
В |
Г |
|
5 |
|
|
|
Завдання 3.
Письмово виконай вправи:
- Запиши рівняння кола з центром у точці О (– 3; 5), яке проходить через точку А (1; 2).
-
Знайди координати точки перетину прямих
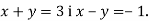
- Обчисли периметр чотирикутника АСВD, якщо А (– 1; 3), В (1; 5), С(3; 3), D (1;1).
-
Склади рівняння прямої, яка проходить через точку (6; 0) і центр кола, заданого рівнянням
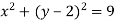 .
.
-
Знайди координати четвертої вершини паралелограма, три вершини якого мають координати
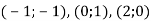 .
.
Блок №2. Вектори на площині
Урок №1

Вектори на площині
«Геометрія – наше велике
творіння, яке нас самих захоплює»
Ле Корбюзьє, французький архітектор
Питання
- Поняття вектора.
- Координати вектора.
- Дії над векторами.
- Скалярний добуток векторів.
Література
Істер О.С. Геометрія: Підручник для 9 класу, §6 – 10, стор. 54 – 93.
|
1. Поняття вектора |
||
|
1.1 |
Вектором називається напрямлений відрізок. |
А А – початок, В – кінець |
|
1.2 |
Довжиною (модулем вектора) називають відстань між його початком і кінцем: |
|
|
1.3 |
Вектор, у якого початок і кінець співпадають називають нуль – вектором і позначають
Довжина нуль – вектора дорівнює 0: |
|
|
1.4 |
Вектор, який має довжину 1, називають одиничним вектором і позначають
|
|
|
1.5 |
Два ненульові вектори називаються колінеарними, якщо вони лежать на одній прямій або на паралельних прямих. |
|
|
1.6 |
Колінеарні вектори, які мають однаковий напрям називаються співнапрямленими, різні напрями – протилежно напрямленими. |
|
|
1.7 |
Вектори називаються рівними, якщо вони співнапрямлені і мають однакову довжину.
|
|
|
1.8 |
Якщо два вектори мають рівні довжини, але протилежні напрями, їх називають протилежними векторами. |
|
|
2. Координати вектора |
||
|
2.9 |
Якщо (Щоб знайти координати вектора потрібно від координат кінця вектора відняти відповідні координати його початку) |
Позначення:
|
|
2.10 |
Якщо |
|
|
2.11 |
Вектори рівні тоді і тільки тоді, коли їх відповідні координати рівні. |
|
|
2.12 |
Вектори колінеарні тоді і тільки тоді, коли їх відповідні координати пропорційні. |
|
|
3. Дії над векторами |
||
|
3.13 |
Щоб додати вектори, їх відповідні координати додають. |
|
|
3.14 |
Для будь – яких точок А, В і С справджується рівність:
|
А С Правило трикутника
Правило паралелограма |
|
3.15 |
Щоб відняти вектори, їх відповідні координати віднімають. |
|
|
3.16 |
Для будь – яких точок А, В і С справджується рівність:
|
А С |
|
3.17 |
Властивості додавання векторів:
1)
2)
3) |
|
|
3.18 |
Щоб помножити вектор на число, його координати множать на це число. |
|
|
4. Скалярний добуток векторів |
||
|
4.19 |
Скалярним добутком векторів |
|
|
4.20 |
Властивості скалярного добутку векторів:
Для будь – яких векторів
1)
2) |
|
|
4.21 |
Кут між векторами
О
|
|
|
4.22 |
Теорема. |
|
|
4.23 |
Наслідки з теореми
1)
2) якщо
3) якщо |
|
Уроки №2, 3
«Коли несправедливі ростуть, як трава, і цвітуть
всі злочинці, то на те, щоб навіки були вони знищені»
Псалом 92:8
Фронтальне опрацювання матеріалу
Вектор. Модуль і напрям вектора. Рівність векторів. Координати вектора. Колінеарні вектори
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 2.12 блоку № 2.
- Усно дай відповіді на питання:
- Що називають вектором?
- Що називають довжиною (модулем) вектора?
- Який вектор називають нуль-вектором?
- Який вектор називають одиничним вектором?
- Які вектори називаються колінеарними?
- Які колінеарні вектори називаються співнапрямленими, протилежно напрямленими?
- Які вектори називаються рівними?
- Які вектори називаються протилежними?
- Як знайти координати вектора?
- Записати формулу для обчислення довжини вектора, якщо відомі його координати.
- Сформулюй умову рівності векторів.
- Сформулюй умову колінеарності векторів.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 2.
2.1. Усно виконай вправи, запропоновані вчителем у презентації.
2.2. Письмово виконай вправи, стор. 58 – 59 підручника: 277; 281; 283.
Завдання 3.
Письмово виконай вправи:
-
Дано точки
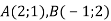 . Знайди координати вектора
. Знайди координати вектора 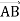 .
.
-
Знайди модуль вектора
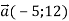 .
.
-
Знайди модуль вектора
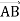 , якщо: 1)
, якщо: 1) 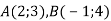 ; 2)
; 2) 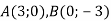 .
.
Завдання 4.
Письмово виконай вправи:
-
Чи колінеарні вектори
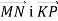 , якщо
, якщо 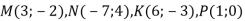 ?
?
-
Знайди значення k, при якому вектори
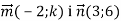 колінеарні.
колінеарні.
-
Дано точки
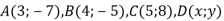 . Знайди х та у, якщо
. Знайди х та у, якщо 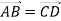 .
.
-
Доведи, що чотирикутник
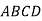
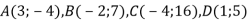 є паралелограмом.
є паралелограмом.
-
Дано координати трьох вершин паралелограма
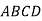
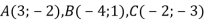 . Знайди координати вершини
. Знайди координати вершини 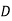
-
Модуль вектора
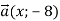 дорівнює 10. Знайди х.
дорівнює 10. Знайди х.
-
Дві вершини прямокутника
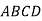
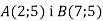 . Модуль вектора
. Модуль вектора 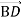 дорівнює 13. Знайди координати точок С і D.
дорівнює 13. Знайди координати точок С і D.
Уроки №4, 5
«Ми ніколи не отримаємо те, що хочемо,
доки не будемо вдячні за те, що маємо…»
Народна мудрість
Фронтальне опрацювання матеріалу
Додавання і віднімання векторів. Множення вектора на число
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 3.18 блоку № 2.
- Усно дай відповідь на питання:
- Що називають вектором?
- Що називають довжиною (модулем) вектора?
- Який вектор називають нуль-вектором?
- Який вектор називають одиничним вектором?
- Які вектори називаються колінеарними?
- Як знайти координати вектора?
- Запиши формулу для обчислення довжини вектора, якщо відомі його координати.
- Сформулюй умову рівності векторів.
- Сформулюй умову колінеарності векторів.
- Як додати вектори?
- Сформулюй правило трикутника.
- Сформулюй правило паралелограма.
- Як відняти вектори?
- Як помножити вектор на число?
- Сформулюй властивості додавання векторів.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 2.
2.1. Вправа: «Морський бій» (самостійно визнач правильну відповідь і знайди ключове слово)
- Що таке вектор?
а) вектор – це напрямлений відрізок;
б) вектор – це відрізок, що має координати;
в) вектор – це пряма, що має напрям.
- Нульовий вектор – це…
а) вектор, абсолютна величина якого не існує;
б) вектор, у якого початок співпадає з його кінцем;
в) вектор, що не має ні початку, ні кінця.
- Які вектори називаються колінеарними?
а) якщо вони не лежать на одній прямій;
б) якщо вони лежать на одній прямій або паралельних прямих;
в) якщо вони не паралельні одній прямій.
- Які два вектори є рівними?
а) якщо вони співнапрямлені;
б) якщо вони мають рівні довжини;
в) якщо вони співнапрямлені і мають рівні довжини.
- Вектори зображені на рисунку
![]()
![]() а) колінеарні;
а) колінеарні;
б) рівні;
в) протилежні.
-
На площині позначено точки A і B. Якими є вектори
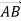 і
і 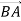 ?
?
а) рівні;
б) мають одинакові довжини;
в) співнапрямлені.
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
а |
Н |
Ф |
Ш |
С |
Я |
Е |
|
б |
В |
А |
П |
Ю |
Г |
М |
|
в |
Д |
Б |
У |
Р |
Ю |
Х |
- Пригадайте алгоритми знаходження суми векторів за правилом трикутника і паралелограма (презентація вчителя).
-
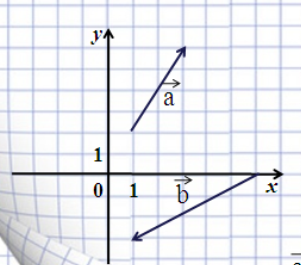 Використовуючи дані алгоритми, виконай вправу: Побудуйте суму векторів
Використовуючи дані алгоритми, виконай вправу: Побудуйте суму векторів 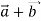 за правилами трикутника і паралелограма та за допомогою координат.
за правилами трикутника і паралелограма та за допомогою координат.
-
Дано вектори
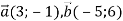 . Знайди: 1)
. Знайди: 1) 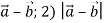 .
.
-
Зобрази довільний вектор
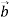 . Побудуй: 1)
. Побудуй: 1) 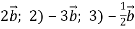 .
.
Завдання 3.
Письмово виконай вправи:
-
Дано вектори
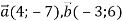 . Знайди координати вектора: 1)
. Знайди координати вектора: 1) 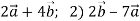 .
.
-
Знайди модуль вектора
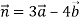 , де
, де 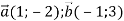 .
.
-
На сторонах ВС, CD паралелограма АВСD взято точки K і L відповідно, причому
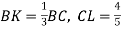 CD. Вирази вектори
CD. Вирази вектори 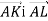 через вектори
через вектори 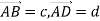 .
.
ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач і вправ
Завдання 4.
Письмово виконай вправи:
-
Дано точки
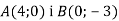 . Знайди координати точки С такої, що
. Знайди координати точки С такої, що 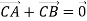 .
.
-
Дано вектори
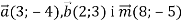 . Знайди такі числа х і у, що
. Знайди такі числа х і у, що 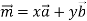 .
.
Уроки №6, 7
«Люди бувають нерозумні, нелогічні
та егоїстичні: все одно прощайте їм»
Мати Тереза
Фронтальне опрацювання матеріалу
Скалярний добуток векторів
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 4.19 – 4.23 блоку № 2.
- Усно дай відповідь на питання:
- Поясни, що таке кут між двома векторами.
- Дай визначення скалярного добутку векторів.
- Сформулюй теорему про скалярний добуток векторів.
- Сформулюй наслідки з теореми про скалярний добуток.
Завдання 2.
Усно виконай вправи, запропоновані вчителем у презентації.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
Письмово виконай вправи, стор. 82, 83 підручника: 394; 396; 401.
Завдання 4.
Письмово виконай вправи, стор. 83, 84 підручника: 403 (2; 4); 411; 416.
Завдання 5.
Письмово виконай вправи:
-
Дано вектори: 1)
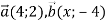 ; 2)
; 2) 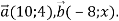 При якому значенні
При якому значенні 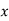
-
Дано вектори
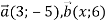 . При яких значеннях х кут між векторами
. При яких значеннях х кут між векторами 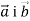 : 1) гострий; 2) прямий; 3) тупий?
: 1) гострий; 2) прямий; 3) тупий?
ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач і вправ
Завдання 6.
Письмово виконай вправи:
-
Знайди косинуси кутів трикутника АВС та визнач його вид, якщо
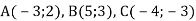 .
.
-
Відрізок АD – медіана трикутника АВС. Знайди модуль вектора
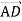 , якщо
, якщо 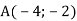 ,
, 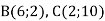 .
.
-
Трикутник АВС задано координатами вершин
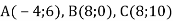 . Знайди довжину висоти СD трикутника АВС, якщо відомо, що ордината точки D удвічі менша від її абсциси.
. Знайди довжину висоти СD трикутника АВС, якщо відомо, що ордината точки D удвічі менша від її абсциси.
-
Трикутник АВС задано координатами вершин
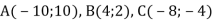 . Знайди довжину висоти AD трикутника АВС, якщо відомо, що ордината точки D на 1 одиничний відрізок більша від її абсциси.
. Знайди довжину висоти AD трикутника АВС, якщо відомо, що ордината точки D на 1 одиничний відрізок більша від її абсциси.
 Готуємось до індивідуального опрацювання матеріалу
Готуємось до індивідуального опрацювання матеріалу
-
Дано вектори
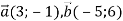 . Знайди: 1)
. Знайди: 1) 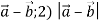 .
.
-
Зобрази довільний вектор
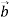 . Побудуй: 1)
. Побудуй: 1) 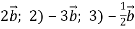 .
.
-
Дано вектори
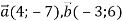 . Знайди координати вектора: 1)
. Знайди координати вектора: 1) 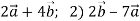 .
.
-
На сторонах ВС, CD паралелограма АВСD взято точки K і L відповідно, причому
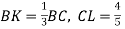 CD. Вирази вектори
CD. Вирази вектори 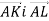 через вектори
через вектори 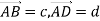 .
.
-
Дано вектори
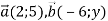 . При якому значенні
. При якому значенні 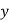
-
Знайди косинус кута А трикутника АВС та визнач його вид, якщо
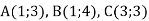 .
.
Урок №9
«В математичних питаннях не можна
нехтувати навіть найменшими помилками»
Ісаак Ньютон, англійський вчений
Внутрішньопредметне узагальнення матеріалу
Вектори на площині
І. Систематизація та узагальнення теоретичних знань
Завдання 1.
- Повтори блок № 2. Особливу увагу зверни на тези 1.1, 1.2, 1.5, 1.7, 2.9, 2.10, 2.11, 2.12, 3.13, 3.18, 4.19, 4.22.
- Дай письмово відповідь на питання, запропоновані вчителем.
ІІ. Систематизація та узагальнення практичних умінь та навичок
Завдання 2.
Усно виконай вправи:
![]()
![]()
![]()
![]() В С
В С
-
 АВСD – квадрат. Яка з наведених рівностей правильна?
АВСD – квадрат. Яка з наведених рівностей правильна?
А D
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Знайди координати вектора
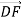 , якщо F
, якщо F 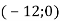 , D
, D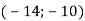 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Знайди абсолютну величину вектора
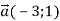 .
.
|
А |
Б |
В |
Г |
|
|
|
|
10 |
Завдання 3.
Письмово виконай вправи:
-
Знайди координати вектора
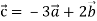 , якщо
, якщо 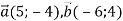 .
.
-
При якому значенні m вектори
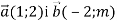 колінеарні?
колінеарні?
-
При якому значенні с вектори
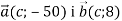 перпендикулярні?
перпендикулярні?
-
Знайди косинус кута між векторами
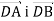 , якщо
, якщо 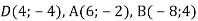 .
.
-
Відрізок АN – медіана трикутника АВС. Знайди модуль вектора
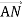 , якщо
, якщо 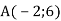 ,
, 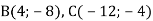 .
.
-
Трикутник АВС задано координатами вершин
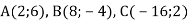 . Знайди довжину висоти AD трикутника АВС, якщо відомо, що ордината точки D на 2 одиничних відрізки менша від її абсциси.
. Знайди довжину висоти AD трикутника АВС, якщо відомо, що ордината точки D на 2 одиничних відрізки менша від її абсциси.
Блок №3. Розв’язування трикутників
Урок №1

Розв’язування трикутників
«Заняття геометрією непомітно
приводить людський розум до винаходів»
Дені Дідро, французький філософ
Питання
- Тригонометричні функції кутів від 0⁰ до 180⁰.
- Співвідношення між сторонами і кутами у довільному трикутнику.
- Розв’язування трикутників.
- Формули для знаходження площі трикутника.
Література
Істер О.С. Геометрія: Підручник для 9 класу, §2, 11 – 14, стор. 12 – 21, 94 – 138.
|
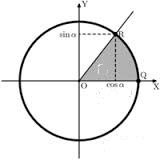
1. Тригонометричні функції кутів від 0⁰ до 180⁰ |
|||||||||||||||||||||||
|
|
R (х; у)
|
||||||||||||||||||||||
|
1.2 |
Основні тригонометричні тотожності Для будь – якого кута α, 0⁰ ‹ α ‹ 180⁰,
|
sin 120⁰ = sin (180⁰ - 60⁰) = sin 60⁰ = |
|||||||||||||||||||||
|
|
|||||||||||||||||||||||
|
2. Співвідношення між сторонами і кутами у довільному трикутнику |
|||||||||||||||||||||||
|
А
с b
а С |
|||||||||||||||||||||||
|
2.3 |
Теорема косинусів. Квадрат будь – якої сторони трикутника дорівнює сумі квадратів двох інших сторін без подвоєного добутку цих сторін на косинус кута між ними. |
|
|||||||||||||||||||||
|
2.4 |
Теорема синусів. Сторони трикутника пропорційні до синусів протилежних кутів. |
R – радіус описаного кола |
|||||||||||||||||||||
|
2.5 |
У трикутнику проти більшого кута лежить більша сторона, проти більшої сторони лежить більший кут. |
||||||||||||||||||||||
|
2.6 |
Якщо |
||||||||||||||||||||||
|
2.7 |
Якщо |
||||||||||||||||||||||
|
2.8 |
Якщо |
||||||||||||||||||||||
|
3. Розв’язування трикутників |
|||||||||||||||||||||||
|
3.9 |
Розв’язати трикутник означає знайти невідомі сторони і кути трикутника за відомими його кутами і сторонами.
Сторони позначають |
||||||||||||||||||||||
|
4. Формули для знаходження площі трикутника |
|||||||||||||||||||||||
|
4.10 |
|
||||||||||||||||||||||
Урок №2
«Без бажання все важке, навіть найлегше»
Григорій Сковорода
Фронтальне опрацювання матеріалу
Синус, косинус і тангенс кутів від 0º до 180º.
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 1.2 блоку № 3.
- Усно дай відповідь на питання:
- Що називають синусом, косинусом, тангенсом кута від 0º до 180º?
- Допиши формулу:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Завдання 2.
Усно виконай вправи 32, стор. 18.
ІІ. Відпрацювання умінь і навичок розв’язування вправ
Завдання 3.
Письмово виконай вправи, стор. 18 – 19 підручника: 34, 36 (1, 3, 5), 46 (1), 51.
Уроки №3, 4
«Розум полягає не тільки в знанні, а й
умінні застосувати знання на ділі»
Аристотель
Фронтальне опрацювання матеріалу
Теорема косинусів
І. Робота над засвоєнням понять, означень, правил
Завдання 1.
- Повторіть тези 1.1 – 2.3 блоку №3
- Дайте відповіді на питання:
- Що називають синусом, косинусом, тангенсом кута від 0º до 180º?
- Допиши формулу:
![]()
![]()
![]()
![]()
![]()
-
 Сформулюйте теорему косинусів.
Сформулюйте теорему косинусів.
- Дано трикутник АВС.
За теоремою косинусів маємо:
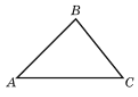
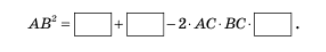
- Дано трикутник АВС.
За теоремою косинусів маємо:

ІІ. Відпрацювання умінь і навичок, застосування правил
Завдання 2.
-
Обчисліть сторону трикутника, якщо інші його сторони дорівнюють 3 і 5, а кут між ними становить
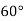
-
Обчисліть сторону трикутника, якщо інші його сторони дорівнюють 5 см і 12 см, а кут між ними становить
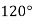
Завдання 3.
-
Знайдіть периметр трикутника, якщо його сторони завдовжки 7 см і 15 см утворюють кут
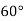
-
У паралелограмі знайдіть довжину меншої сторони, якщо його діагоналі завдовжки
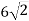 см і 14 см перетинаються під кутом
см і 14 см перетинаються під кутом 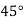
Завдання 4.
- Не обчислюючи кути трикутника, встановіть його вид (за кутами), якщо сторони дорівнюють 6, 10 і 11 см.
- Сторони трикутника дорівнюють 5, 6 і 7 см. Знайдіть косинус одного з кутів і визначте вид трикутника (за кутами).
ІІІ. Відпрацювання умінь та навичок розв’язування нестандартних задач
Завдання 5.
Побудуйте трикутник АВС, якщо АВ=3 см, ВС = 4 см, ![]()
Уроки №5, 6
«Ти щасливий не тому, що все
добре, а все добре тому, що ти щасливий»
Народна мудрість
Фронтальне опрацювання матеріалу
Теорема синусів
 І. Робота над засвоєнням понять, визначень, правил
І. Робота над засвоєнням понять, визначень, правил
Завдання 1.
- Повтори тези 1.1 – 2.8 блоку № 3.
- Усно дай відповідь на питання:
- Сформулюй теорему косинусів.
- Сформулюй теорему синусів.
- Сформулюй правила співвідношень між мал. 1
сторонами і кутами трикутника.
Завдання 2.
Усно виконай вправи:
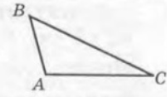
- Дано трикутник АВС (мал.1). За теоремою синусів маємо:
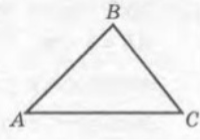
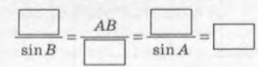
- Дано трикутник АВС (мал.2). За теоремою синусів маємо:
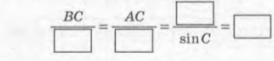
ІІ. Відпрацювання умінь та навичок, застосування правил мал.2
Завдання 3.
Усно виконай вправи:
-
Обчисли
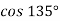
|
А |
Б |
В |
Г |
|
|
1 |
– 1 |
|
В
-

 Якщо у трикутнику АВС
Якщо у трикутнику АВС 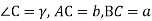
![]() А С
А С
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Якщо у трикутнику АВС
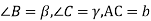
|
А |
Б |
В |
Г |
|
|
|
|
|
Завдання 4.
Письмово виконай вправи:
-
У трикутнику АВС
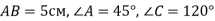
-
У трикутнику АВС
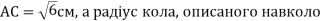 цього трикутника дорівнює
цього трикутника дорівнює 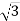 см. Знайди градусну міру кута В.
см. Знайди градусну міру кута В.
-
Дві сторони трикутника дорівнюють
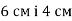
- Обчисли косинуси кутів трикутника зі сторонами 7 м, 24 м, 25 м та визнач його вид (за кутами).
-
Сторони паралелограма дорівнюють 1см і
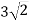 см, а гострий кут між ними – 45⁰. Знайди більшу діагональ паралелограма.
см, а гострий кут між ними – 45⁰. Знайди більшу діагональ паралелограма.
-
У прямокутному трикутнику АВС з гіпотенузою АС знайди бісектрису ВD, якщо
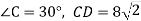 см.
см.
-
Радіус кола, описаного навколо рівнобедреного трикутника з кутом
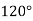
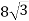 см. Знайди сторони трикутника.
см. Знайди сторони трикутника.
Завдання 5.
Письмово виконай тестування, запропоноване вчителем у презентації. За це ти можеш отримати додаткові бали.
ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач
Завдання 6.
Накресли рівнобедрений трикутник з кутом при основі![]()
Уроки №7, 8
«Справжній скарб для людини – вміння трудитися»
Езоп
Фронтальне опрацювання матеріалу
Розв’язування трикутників
І. Робота над засвоєнням термінів, понять і правил
Завдання 1.
- Повтори тези 1.1 – 3.9 блоку № 3.
- Усно дай відповідь на питання:
- Назви вид трикутника:
а) У трикутника дві сторони рівні і один кут дорівнює 90°.
б) У трикутнику дві сторони рівні і один кут дорівнює 120°.
в) У трикутнику всі кути по 60°.
- Вставте пропущені слова:
а) У трикутнику проти … лежить більший кут, проти більшого кута лежить …
б) Теорему косинусів називають іноді узагальненою теоремою …
в) … і … трикутника називаються основними його елементами.
г) Розв’язати трикутник означає: за даними … основними елементами трикутника … . При цьому серед заданих основних елементів хоча б один повинен бути …
- Знайди зайве слово:
СТОРОНА, ВЕРШИНА, ДІАМЕТР, ОСНОВА, ПЕРИМЕТР.
- Скільки трикутників на малюнку?
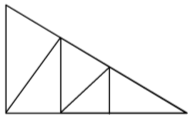
-
Сторони трикутника дорівнюють m, n, p і
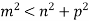 . Тоді кут, протилежний стороні m, буде…
. Тоді кут, протилежний стороні m, буде…
|
А |
Б |
В |
Г |
|
Прямий |
Тупий |
Гострий |
Розгорнутий |
![]()
![]() В
В
-
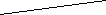 У трикутнику СВD
У трикутнику СВD 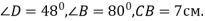 D Тоді сторону СD можна знайти з рівності… С
D Тоді сторону СD можна знайти з рівності… С
|
А |
Б |
В |
Г |
|
|
|
|
|
![]()
![]() Y
Y
-
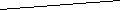 У трикутнику XYZ
У трикутнику XYZ 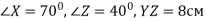 . Як обчислити радіус R кола, описаного навколо X Z трикутника?
. Як обчислити радіус R кола, описаного навколо X Z трикутника?
|
А |
Б |
В |
Г |
|
|
|
|
|
ІІ. Відпрацювання умінь і навичок, застосування правил
Завдання 2.
Письмово виконай вправи:
- Визнач вид трикутника за кутами, якщо його сторони дорівнюють:
-
3 см, 5 см, 7 см; 2) 1 см,
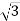 см, 1 см.
см, 1 см.
- Дві сторони трикутника дорівнюють 5 см і 7 см, а кут між ними 60°. Знайди третю сторону трикутника.
- Сторона трикутника дорівнює 10 см , а прилеглі до неї кути – 45° і 75°. Знайди сторону, протилежну до кута 45°.
- Сторони трикутника дорівнюють 6 см, 9 см, 8 см. Знайти косинус кута, який лежить проти більшої сторони.
Завдання 3.
- Розглянь додаток до блоку про основні задачі на розв’язування трикутників.
- Користуючись розглянутим матеріалом, усно дай відповідь на питання:
- Що означає розв’язати трикутник?
- Скільки існує типів задач на розв’язування трикутників?
- Сформулюй план розв’язування кожного типу задач.
Завдання 4.
Користуючись додатком до блоку та презентацією вчителя, письмово виконай вправи:
- Знайти невідомі сторони і кути трикутника АВС, якщо:
-
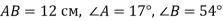
-
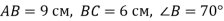
-
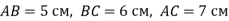
-
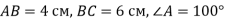
- Одна із сторін трикутника дорівнює 30 см, а прилеглі до неї кути 60° і 45°. Знайди невідомі сторони і кути трикутника.
Урок №9
«Мислить той, кому ставлять розумні запитання»
Народна творчість
Фронтальне опрацювання матеріалу
Розв’язування прикладних задач
І. Робота над засвоєнням термінів, понять і правил
Завдання 1.
- Повтори тези 1.1 – 3.9 блоку № 3.
- Усно дай відповідь на питання:
- Сформулюй теорему косинусів.
- Сформулюй теорему синусів.
- У якому співвідношенні перебувають сторони і кути трикутника?
- Як, маючи сторони трикутника, визначити його вид за кутами?
- Що означає розв’язати трикутник?
Завдання 2.
- Розглянь презентацію, запропоновану вчителем.
- Дай відповіді на питання:
- Що таке прикладна задача?
- Які типи прикладних задач розв’язуються за допомогою розв’язування трикутників?
ІІ. Відпрацювання умінь і навичок, застосування правил
Завдання 3.
Письмово виконай вправи:
- За даними малюнка знайди відстань між недоступними точками А і В:
-
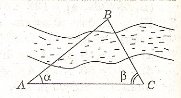
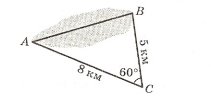 2)
2) 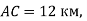
![]()
![]()
-
Футбольний м’яч знаходиться в точці А футбольного поля на відстані 4,5 метрів і 9,4 метрів від основ В і С стійок воріт (мал. 3). Футболіст направляє м’яч у ворота. Знайдіть кут
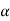

Урок №10
«Геометрія є найміцнішим засобом для витонченості
наших розумових здібностей та дає можливість
правильно мислити та міркувати»
Г.Галілей
Фронтальне опрацювання матеріалу
Трикутники та їх розв’язування
І. Робота над засвоєнням термінів, понять і правил
Завдання 1.
- Повтори тези 1.1 – 3.9 блоку № 3.
- Усно дай відповідь на питання:
- Сформулюйте теорему косинусів.
- Що означає розв’язати трикутник?
- Сформулюйте теорему синусів.
-
Які є співвідношення між сторонами і кутами трикутника?
- Запам’ятайте рекомендації на урок, запропоновані вчителем у презентації.
ІІ. Відпрацювання умінь і навичок, застосування правил
Завдання 2.
2.1. Відкриття Приватного детективного агентства.
Сьогодні я пропоную вам узяти участь у пошуку двох підозрюваних. На основі результатів пошуку я зроблю висновки про професійну придатність кожного з вас.
Бажаю вам успіху!!! Вам необхідно поділитись на дві групи.
2.2. Установлення осіб підозрюваних і складання їхніх портретів
Перед кожною групою стоїть наступне завдання: визначити підозрюваного та скласти його портрет-фоторобот (на дошці).
Група має час на обмірковування 2 хвилини. Після цього начальник слідчої групи має визначити учня, який встановить особу підозрюваного.
Завдання 3. Слідчий експеримент
3.1. Розв’язати кросворд «Трикутник». Визначити ключове слово кросворда.
3.2. Вставити пропущені слова, запропоновані вчителем у презентації.
Завдання 4.
Наші підозрювані мають одну небезпечну властивість. Вони вміють перевтілюватися і ви повинні навчитися розпізнавати їх за будь-яких обставин. Тому необхідно виконати наступне завдання.
Завдання для слідчих груп
Визначити вид трикутника за кутами:
Завдання для І слідчої групи
У підозрюваного № 1 сторони дорівнюють 3 см, 5 см, 7 см. Який вид трикутника?
Завдання для II слідчої групи
У підозрюваного № 2 сторони дорівнюють 10 см, 8 см, 6 см. Який вид трикутника?
Завдання 5. Проведення експертизи речових доказів
Двох підозрюваних ми відшукали, залишився ще один. Ми знаємо його ім’я – РІЗНОСТОРОННІЙ ТРИКУТНИК. Нам необхідно провести експертизу речових доказів. Завдання для кожної слідчої групи.
І слідча група.
Дві сторони трикутника дорівнюють 5 см і 7 см, а кут між ними 60°. Знайдіть третю сторону трикутника.
ІІ слідча група.
Сторона трикутника дорівнює 10 см, а прилеглі до неї кути - 45° і 75°. Знайти сторону протилежну до кута 45°.
Ми знайшли всіх підозрюваних. І всі можуть бути зараховані до штату детективного агентства.
 Готуємось до індивідуального опрацювання матеріалу
Готуємось до індивідуального опрацювання матеріалу
- Одна зі сторін трикутника дорівнює 36 см, а прилеглі до неї кути – α = 60º і β = 95º. Знайди сторону, протилежну до кута α.
- Знайди невідомі сторони і кути трикутника АВС, якщо:
-
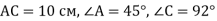
-
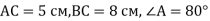
Уроки №12, 13
«Без бажання все важке, навіть найлегше»
Григорій Сковорода
Фронтальне опрацювання матеріалу
Розв’язування задач на знаходження площі трикутника
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тезу 4.10 блоку № 3.
- Запиши формулу для обчислення площі трикутника через:
- сторону і висоту, проведену до неї;
- дві сторони і кут між ними;
- півпериметр і радіус вписаного кола;
-
сторони і радіус описаного кола;
- Запиши формули для обчислення площі трикутника:
- Герона;
- прямокутного;
- правильного.
Завдання 2.
- Усно розв’яжи вправи:
- Знайди площу трикутника, якщо його сторони дорівнюють 3 см і 4 см, а кут між ними 30⁰.
|
А |
Б |
В |
Г |
|
2 см ² |
6 см ² |
1,5 см ² |
|
- Знайди площу трикутника, якщо його сторони дорівнюють 2 см, 8 см, 6 см, а радіус описаного кола дорівнює 2 см.
|
А |
Б |
В |
Г |
|
30 см ² |
60 см ² |
7,5 см ² |
|
- Знайди площу трикутника, якщо його сторони дорівнюють 5 см, 5 см, 8см.
|
А |
Б |
В |
Г |
|
32 см ² |
60 см ² |
48 см ² |
12 см ² |
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
Письмово розв’яжи вправи:
- Знайдіть найменшу висоту трикутника, сторони якого дорівнюють 7 см, 8 см і 9 см.
-
Дві сторони трикутника дорівнюють 4 см і 8 см, а його площа – 12
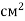 . Обчислити кут між цими сторонами, якщо відомо, що він тупий.
. Обчислити кут між цими сторонами, якщо відомо, що він тупий.
-
Площа рівнобедреного трикутника дорівнює 150
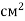 , а кут при вершині
, а кут при вершині 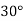
Завдання 4.
Письмово розв’яжи вправи:
- Знайти площу паралелограма, якщо його сторони дорівнюють 3 см і 8 см, а один з кутів 45⁰.
- Сторони трикутника дорівнюють 5см, 5 см і 8 см. Знайти найменшу висоту трикутника.
- Площа рівнобедреного трикутника дорівнює 16 см ², а його основа – 8 см. Знайти інші сторони трикутника і радіус кола, описаного навколо нього.
 Готуємось до індивідуального опрацювання матеріалу
Готуємось до індивідуального опрацювання матеріалу
- Знайти площу паралелограма, якщо його сторони дорівнюють 5 см і 4 см, а один з кутів 45⁰.
- Дві сторони трикутника дорівнюють 5 см і 4 см, а його площа 5 см ². Обчислити кут між цими сторонами, якщо відомо, що він гострий.
- Сторони трикутника дорівнюють 10см, 9 см і 17 см. Знайти найбільшу висоту трикутника.
- Площа рівнобедреного трикутника дорівнює 12 см ², а його основа – 4 см. Знайти інші сторони трикутника і радіус кола, описаного навколо нього.
Урок №15
«І все, що тільки чините,
робіть від душі, як Господу, а не людям»
Послання св. апостола Павла до Колосян 3 : 23
Внутрішньопредметне узагальнення матеріалу
Розв’язування трикутників
І. Систематизація та узагальнення теоретичних знань
Завдання 1.
- Повтори блок № 3.
- Дай письмово відповідь на питання, запропоновані вчителем.
Завдання 2.
Усно виконай вправи:
-
Сторони трикутника дорівнюють m, n, p і
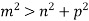 . Тоді кут, протилежний стороні m, буде…
. Тоді кут, протилежний стороні m, буде…
|
А |
Б |
В |
Г |
|
Прямий |
Тупий |
Гострий |
Розгорнутий |
B
-

 У трикутнику СВD
У трикутнику СВD 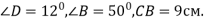 D Тоді сторону СD можна знайти з рівності… C
D Тоді сторону СD можна знайти з рівності… C
|
А |
Б |
В |
Г |
|
|
|
|
|
- Знайдіть площу трикутника, якщо його сторони дорівнюють 12 см і 16 см, а кут між ними 30⁰.
|
А |
Б |
В |
Г |
|
6 см ² |
12 см ² |
24 см ² |
48 см ² |
ІІ. Систематизація та узагальнення практичних умінь та навичок
Завдання 3.
Письмово виконай вправи:
-
У паралелограмі АВСD
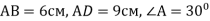
-
У трикутнику АВС
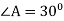
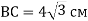 . Знайдіть сторону АС.
. Знайдіть сторону АС.
- Сторони трикутника дорівнюють 9 см, 12 см і 15 см. Знайти найбільшу висоту трикутника.
- Знайдіть радіуси вписаного і описаного кіл трикутника зі сторонами 24см, 26см, 10см.
~ 1 ~


про публікацію авторської розробки
Додати розробку