Навчальний посібник "МАТЕРІАЛИ ДЛЯ ПІДГОТОВКИ УЧНІВ 7 КЛАСУ ДО МАТЕМАТИЧНОЇ ОЛІМПІАДИ"

МАТЕРІАЛИ

ДЛЯ ПІДГОТОВКИ УЧНІВ 7 КЛАСУ

ДО МАТЕМАТИЧНОЇ ОЛІМПІАДИ

Навчальний посібник

 

 

Автор: Слободян Валентина Вікторівна,

                                 вчитель математики

                                    Хмельницького НВО№28

 

 

 

 

 

 

 

 

 

 

 

ВСТУП

Розв’язування  вправ підвищеної складності з учнями середніх класів без певної системи не дає великого ефекту. Тільки послідовне розв’язання задач одного типу виробляє правильний підхід до них, формує вміння аналізувати задану ситуацію, розвиває творче мислення і здібності.

В посібнику систематизовані вправи творчого характеру за темами:

1.              Використання запису загального вигляду  натуральних чисел у вигляді суми розрядних одиниць.
2.              Подільність чисел.
3.              Ділення з остачею. Періодичність остачі.
4.              Прості числа. Взаємно прості числа.
5.              Найбільший спільний дільник. Найменше спільне кратне.

 

 

 

1. ВИКОРИСТАННЯ ЗАПИСУ ЗАГАЛЬНОГО ВИГЛЯДУ НАТУРАЛЬНИХ ЧИСЕЛ У ВИГЛЯДІ СУМИ РОЗРЯДНИХ ОДИНИЦЬ.

 

Приклад 1. Знайти двохзначне число, яке у 4 рази більше суми його цифр.

Розв’язання. Нехай двохзначне число у вигляді 10а + b, де а- число десятків, а b- число одиниць. Складаємо рівняння:

10а+b=4(a+b);

6a=3a;

b=2a;

a=.

Шляхом відбору цифр знаходимо b=2; 4; 6; 8;, a=1; 2; 3; 4.

Шукані числа: 12, 24, 36, 48.

Приклад 2. Якщо між цифрами двохзначного числа вписати те саме число, то одержане чотирьохзначне число буде більше даного двохзначного числа в 77 разів. Знайдіть це число.

Розв’язання.Нехай дане двохзначне число , тоді - отримане чотирьохзначне число. Маємо , або . Отже, 5a=b. Тому a=1, b=5.

Шукане число 15.

Приклад 3. Серед двохзначних чисел знайдіть таке число, куб суми цифр якого дорівнює квадрату самого числа.

Розвязання. Нехай - дане число. Маємо

.

Отримали Діафантове рівняння в натуральних числах, тобто . Щоб така рівність виконувалася в натуральних числах, необхідно щоб , . Оскільки , то, тому (1.2.3.4). Методом відбору цифр знаходимо, що x=1, 4, 9, a y=1, 8, 27,64.

;

;

.

          Отже, шукане число 27.

 

 

 

Задачі для самостійної роботи.

 

Приклад 1. Чи існує трьохзначне число, яке дорівнює добутку своїх цифр?

Відповідь: Не існує.

Приклад 2. Знайти трьохзначні числа, такі, щоб сума шести двохзначних чисел, складених із цифр цього числа, дорівнювала самому числу.

Відповідь: 132 і 264.

Приклад 3. Для яких двозначних чисел сума куба цифри одиниць і квадрата цифри десятків дорівнює цьому числу.

Відповідь: 43 і 63.

Приклад 4. До якого двохзначного числа треба зліва і справа  приписати по одиниці, щоб в результаті отримати число в 23 рази більше початкового.

Відповідь: 77.

Приклад 5. Знайти двохзначне число , яке дорівнює сумі чисел його десятків і квадрату числа його одиниць.

Відповідь: 89.

 

 

2. ПОДІЛЬНІСТЬ ЧИСЕЛ

 

Приклад 1. Довести, що різниця будь-яких трьохзначних чисел, записаних тими самими цифрами, але в зворотньому порядку, ділиться на 9.

Розв’язання.

Ділиться на 9. Доведено.

Приклад 2. Довести,що коли в трьохзначному числі дві останні цифри однакові, а сума його цифр ділиться на 7, то і саме це число ділиться на7.

Розв’язання

 

- ділиться на 7

- сума цифр ділиться на 7.

Отже, число ділиться на 7.

Приклад 3. Довести, що коли в шестизначному числі перша і четверта цифри рівні, друга і п’ята рівні, а також третя і шоста рівні, то це число кратне 7, 11 і 13.

Розв’язання.

=100000х+10000у+1000z+100x+10y+z= =100100x+10010y+1001z=1001(100x+10y+z), але 1001=7.

З цього слідує, що твердження вірне.

Приклад 4. Знайти найменше натуральне число виду 123х43у, яке ділиться на 3.

Розв’язання.

Сума цифр числа даного виду дорівнює 1+2+3+х+4+3+у=13+х+у.

Найменше значення цієї суми, при якому задане число ділиться на 3, рівне 15, тобто коли х+у=2. Серед усіх чисел даного виду, при умові що х+у=2, має три – 1230432, 1232430, 1231431, з яких найменшим є 1230432.

Крім значення 2, сума х+у може приймати значення 5, 8, 11, 14, 17. У всіх випадках буде отримане число більше за 1230432.

Приклад 5. Довести, що число кратне десяти.

Доведення. Знайдемо якою цифрою закінчується кожний доданок

         7¹ =7

7² – закінчується цифрою 9

7³ – закінчується цифрою 3

7⁴ – закінчується цифрою 1

7⁵ – закінчується цифрою 7.

Далі останні цифри повторюються з періодом 4. З цього слідує, 99:4=24 з остачею 3. Отже, закінчується цифрою 3, так як 7⁴  закінчується цифрою 1.

3⁴⁴  закінчується цифрою 1.

4⁸⁸  закінчується цифрою 6.

Сума закінчується цифрою 0, тому вона кратна 10.

Приклад 6. Довести, що 7ⁿ+3n-1 ділиться на 9 при будь-якому n.

Доведення. Для доведення скористаємося принципом математичної індукції, що полягає у слідуючому: твердження , залежне від натурального числа n , справедливе для будь-якого n коли виконано дві умови:

1.              твердження правильне при n=1
2.              при будь-якому натуральному значенні k із справедливості твердження для n=k випливає його справедливість і для n=k+1.

Нехай n=1. Тоді 7¹+3∙1-1=9. 9=9, тому твердження вірне для n=1.

Припустимо, що (7^k+3k-1) 9.

Доведемо, що  [7^k+1+3(k+1)-1]9.

Дійсно,(7^k+1+3k+3-1)=

=7^k∙7+3k-1+3=7(7^k+3k-1) -18k+9=

              =7(7^k+3k-1)-9(2k-1).

Цей вираз ділиться на 9 так як кожний доданок ділиться на 9.

Приклад 7. Довести, що (11ⁿ⁺²+12²ⁿ⁺¹) ділиться на  133

Доведення. Нехай n=1, тоді 11³+12³=(11+12)∙(11²-11∙12+12²)=23∙133.

Отже,при n=1 твердження вірне.

Припустимо, що (11^k+2+12^2k+1) 133.

Доведемо, що в такому випадку і (11^k+3+12^2k+3)33.

Насправді,11^k+3+12^2k+3=11∙11^k+2+12² ∙12^2k+1=11∙11^k+2+144∙12^2k+1=11(11^k+2+12^2k+1)+ +133∙12^2k+1. Одержана сума ділиться на 133.

Твердження доведено.

 

 

 

 

 

 

Задачі для самостійної роботи.

 

Приклад 1. Знайти найбільшу цифру х, при якій сума 12+12х³ ділиться на 3.

Відповідь. х=7.

Приклад 2. Якими цифрами закінчуються числа виду:

1.              508⁶³ ;            2) 7^4k+1;   3) 8^4k+3, k є N.

Приклад 3. Довести . що значення виразу 96⁷-22⁵-48⁶ кратне 10.

Приклад 4. Довести, що 4²⁶-1 кратне 5.

Приклад 5. Довести методом математичної індукції, що (6²ⁿ -1)35.

 

 

 

 

 

3. ДІЛЕННЯ З ОСТАЧЕЮ.

ПЕРІОДИЧНІСТЬ ОСТАЧІ.

 

Будь-яке ціле число a може бути представленим наступним чином:

або у вигляді a=bq;

або у вигляді a=bq+1;

або у вигляді a=bq+2;

…………………………………;

або у вигляді a=bq+(b-1).

Наприклад, при b=2, a=2q (число ділиться на 2), або у вигляді a=2q+1 (число не ділиться на 2).

Приклад 1. Довести, що при будь-якому цілому  значенні n, число n²+1 не ділиться на 3.

Доведення. Число n може бути представлене у вигляді n=3q. Маємо n²+1=9q²+1. Звідси видно, що n²+1 при діленні на 3 дає остачу 1.

       При n=3q+1;                                                             п²+1=(Зq+1)²=9q²+6q+2=3(3q²+2q)+2 остача 2.

При n=Зq+2; n²+1=(3q+2)²=9q²+12р+5=3(Зq²+4q+1)+2 остача 2. Отже, в будь-якому випадку число n²+1 на 3 не ділиться.

Приклад 2: Доведіть, що які б не були цілі числа а,b,с число а²+b²+с²+1 не ділиться на 8.

Розв 'язання:

Так як а²+b²+с²+1=(а²-1)+(b²-1)+(с²-1)+4; то число а²+b²+с²+1 тільки у тому випадку буде ділитися на 8, якщо (а²-1)+(b²-1)+(с²-1) при діленні на 8 дасть остачу 4.

Якщо число а, не парне (а=2q+1), то(а²-1)=(2q+1)²-      -1=4q(q+1).

Так як число q(q+1) парне то число а²-1 ділиться на 8, тобто а²-1=8к.

Якщо ж а парне (а=2q), то а²=4q² ділиться на 4, отже має вигляд 4(к+1)=4к+4 або 4к+8, а тому число а²-1 може мати вигляд 8к; 8к+3; 8к+7. Аналогічно числа (b²-1) і (с²-1). З цього слідує, що число (а²-1)+(b²-1)+(с²-1) не може при діленні на 8 мати остачу 4.

При будь-яких натуральних а і m, остачі від ділення чисел а; а²; а³; а⁴; а⁵, на m періодично повторюються. Якщо знайдеться такий показник l, то а^l має остачу 1 при діленні на m, то остачі від ділення чисел а; а²; а³; а⁴; а5,.на m періодично повторюються з періодом l.

Приклад 3. Знайти остачу від ділення числа 222⁵⁵⁵ на 7.

Розв 'язання:

Так як 222= 7∙31+5, то 222 при діленні на 7 має остачу 5 і тому 222⁵⁵⁵ при діленні на 7 дає таку ж остачу як 5⁵⁵⁵ . Тепер подивимось як повторюються остачі степенів п'ятірки при діленні на 7.

5²=25 (остача 4)

5³=125 (остача 6)

5⁴=625 (остача 2)

5⁵=3125 (остача 3)

5 ⁶= 15625 (остача 1)

Отже 5⁶¹ при ділені на 7 дає остачу 1 при будь-якому натуральному k, але 555=6∙92+3.

Тому 5⁵⁵⁵ =5^6∙92+3+3=5^6∙92 ∙5³. Таким чином 5⁵⁵⁵ дає остачу 6 при діленні на 7.

З цього слідує, що число   222⁵⁵⁵ дає при діленні на7 остачу 6.

Важливо запам'ятати, що степінь числа при діленні на m і степінь остачі цього числа, дають одну і ту ж остачу при ділені на m. Ця ідея часто використовується для розв'язання вправ.

Приклад 4. Знайти остачу від ділення числа

(3²⁰+11)⁵⁵ на 13.

Розв 'язання:

(3²⁰+11)⁵⁵=[(33)⁶∙3²+11)]⁵⁵=[(26+1)⁶∙3²+11)⁵⁵=(1⁶∙3²++11)⁵⁵=20⁵⁵=(13+7)⁵⁵=7⁵⁵=(7²)²⁷∙7=(13+1)²⁷∙7=1²⁷∙7==7 остача 7.

Приклад 5. Довести, що число 1¹⁹⁹¹+2¹⁹⁹¹+З¹⁹⁹¹+...+30¹⁹⁹¹ ділиться на 31

 Розв 'язання:

Замінимо додатні остачі від'ємними

1¹⁹⁹¹₊2¹⁹⁹¹+...+15¹⁹⁹¹+(-15) ¹⁹⁹¹+...+(-1) ¹⁹⁹¹=0

[16¹⁹⁹¹=(31-15) ¹⁹⁹¹=(-15) ¹⁹⁹¹]

3 цього слідує, що сума ділиться на31.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Задачі для самостійної роботи

 

 

Приклад 1. Довести, що при будь-якому цілому n число n²+n парне.

 

Приклад 2.  Довести, що при будь-якому цілому n число n²-n ділиться на 6.

Вказівка:

Розглянемо n=6q; n=6q+1; n=6q+5; n²-n=n(n-1)∙(п+1)

 

Приклад 3. Довести, що коли сума трьох чисел ділиться на 6, то сума кубів цих чисел ділиться на 6.

Вказівка: 

а³+b³+с³=(а+b+с)+(а³-а)+(b³-b)+(с³-с). Кожне з чисел а³-а= а(а-1)∙(а+1) ділиться на 6.

 

Приклад 4.  Довести, що коли m²+n² ділиться на 3, то цілі числа т і п діляться на 3.

Вказівка:

Якщо m ділиться на 3, то m² ділиться на 3. Якщо т не ділиться на 3, то m² при діленні на 3 дає остачу 1. Так як m=3k+1 або m=Зk+2, де k - ціле число.

Аналогічно з п.Остача суми m²+n² буде 1; 2.

4. ПРОСТІ ЧИСЛА.

ВЗАЄМНО ПРОСТІ ЧИСЛА.

 

                   Дуже часто використовують слідуючу теорему:

                   якщо число п ділиться на кожне з двох взаємно простих числа а і b, то воно ділиться на їх добуток ab.

 

Приклад 1. Доведіть, що при будь-якому непарному п число n³-n ділиться на 24.

Доведення:

Так як n=2k-1, то n³-n=n(n-1)∙(n+1)=(2k-1)∙(2k-2)∙2к=4k(k-1)∙(2k-1).

Число k(k-1) ділиться на 2, значить, n³-n ділиться на 8.

Далі k(k-1)∙(2k-1) ділиться на 3. Оскільки, 8 і 3 взаємно прості числа, то число n³-n ділиться на 24.

 

Приклад 2. Доведіть, що остача від ділення простого числа на 30 є просте число або одиниця.

Доведення:

р:30=q(остача г). Отже р=30q+p.

Якщо р<30, то г=р і значить г -просте число.

Якщо р>30, то остача г=1, 2, 3, 4, 5 ... 29. Закреслимо послідовно числа кратні 2, залишиться 1 або просте число.

 

           Приклад 3.  Знайти всі прості числа р і q для яких р²-2q²=1

         Розв 'язання:

 

Так як q просте число, то q² - просте число у другому степені. Значить (р-1) і    

          

повинні бути однаковими числами.

Це можливо, якщо р=3, а q=2.

 

Приклад 4.  Доведіть, що р²-1 кратне 24, якщо р - просте число, більше 3.

Доведення:

Так як р>30, то числа (р-1) і (р+1) парні.

Добуток послідовних парних чисел ділиться на 4. З трьох послідовних натуральних чисел р-1; р; р+1 одне число ділиться на 3.

р>30 просте число, воно не ділиться на 3. Тому р-1 або р+1 ділиться на 3. А з двох послідовних парних чисел одне ділиться на 4.

Задачі для самостійної роботи

 

 Приклад 1. Доведіть, що числа n і n+1 взаємно прості.

  Вказівка:

 Якщо кожне з чисел n і n+1 ділиться на  натуральне число d, то їх різниця (n+1)-n≠1 ділиться на d.

Тоді d=1.

 

Приклад 2. Чи вірно, що при будь-якому непарному а, число (100+а)⁵+1 завжди буде складеним.

Вказівка:

"Ні". При а=-99 і а=-101.

"Так" при будь-якому натуральному а.

 

Приклад 3. Доведіть, що при простому натуральному п≥5 число n²-1 ділиться на 24.

 

 

 

 

 

 

 

 

5. НАЙБІЛЬШИЙ СПІЛЬНИЙ ДІЛЬНИК. НАЙМЕНШЕ СПІЛЬНЕ КРАТНЕ.

 

Існує досить простий спосіб, який дозволяє знаходити НСД двох натуральних чисел. Цей спосіб називається алгоритмом Евкліда, який можна описати так:

дано два натуральних числа а і b (а>b), поділивши а на b з остачею, одержали а=q₁+r₁. Тепер поділивши b на r₁  одержали: b=q₂∙r₁+r₂. Поділивши далі  r₁ на r₂ з остачею, знайдемо r₁=q₃∙r₂+r₃ і т. д . Остання остача, яка не дорівнює нулю і буде НСД чисел а і b.

Приклад 1.

Знайти НСД чисел 645 і 381. Розв 'язання:

За допомогою алгоритму Евкліда маємо:

645=381-1+264;

381=264-1+117;

264=117-2+30;

117=30-3+27;

30=27-1+3;  

27=3-9+0.

Отже НСД (645;381)=3.

Найменше спільне кратне двох натуральних чисел а і b можна знайти за формулою:

 

 

 

Приклад 2.  Знайти всі пари натуральних чисел, які більше 0 і менше 60, такі, що їх НСД=3, а різниця додатня і кратна 18.

 Розв 'язання:

Ця задача розв'язується перебором об'єм якого потрібно попередньо обмежити.

Введемо позначення: х,у - шукані натуральні числа; НСД(а,b) - функція, значення якої є найбільший спільний дільник чисел а і b. Тоді умову задачі можна записати у такому вигляді:

 

 

 

 

 

 

 

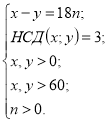
Оскільки ліва частина першого рівняння менше 60, то п<4, крім того, х=3х₁; у=3у₁. Причому НСД (х₁;у₁)=1, а х₁-у₁=6n(х₁<20;у₁<20). Тепер, перебираючи значення n, одержимо необхідну множину розв'язків.

 

а)n=1;

 х₁-у₁=6 => (х₁;у₁) є

{(7;1),(11;5),(13;7),(17;11),(19;13)},тому
(х;у) є {(21;3),(33;15),(39;21),(51;33),(57;39)}; '

б) n=2;

 х₁-у₁=12, тоді (х₁;у₁)  є {(13;1),(17;5),(19;7)}=>

(х;у) є {(39;3),(51;15),(57;21)};

   в) n=3;

 х₁-у₁ = 18; (х₁;у₁) є {(19;1)} =>    (х;у) є {(57;3)}.

Шукана множина містить всі пари, одержані в пунктах а), б), в).

 

 

 

 

 

 

 

 

 

 

 

 

 

Задачі для самостійної роботи

 

Приклад 1. Знайти за допомогою алгоритму Евкліда НСД (846; 246).

Приклад 2. Скоротити дріб  

Відповідь:

 

Приклад 3: Доведіть, що НСД (2n;2n+2)=2 при будь-якому цілому n.

Вказівка: Алгоритм Евкліда: 2n+2=2n∙1+2;2n=2∙n.

 

Приклад 4: Найменше спільне кратне двох чисел, які не діляться одне на одне, дорівнює 90, а їх найбільший спільний дільник 6. Знайти ці числа.

Відповідь: 18 і 30.

 

ЛІТЕРАТУРА

1.   Виноградов И.М. Основи теорії  чисел.
2.   Шнирельман Л.Г. Прості  числа.
3.   Шунда Н.М. Зборник задач по алгебре для 6-8 классов.
4.   Развивающие задачи на уроках математики. Квантор №3-1991 р.
5. Кострикина Н.Т. Решение упражнений повышенной трудности. 7-9 класс.