Навчально методичний посібник "Розв’язування задач логічного характеру з використанням кругів Ейлера" (для учнів 6-8 кл.)
У посібнику зібрані і об'єднані за складністю задачі логічного змісту, які розв'язуються за допомогою діаграм Ейлера-Венна.
Посібник може бути використаний для організації позакласних занять, доповнення уроків математики нестандартними задачами, факультативних занять та підготовки учнів до математичних змагань і олімпіад.
Управління освіти і науки виконкому Криворізької міської ради
Криворізька Центрально-Міська гімназія
Т. Р. Кривоносова
Розв’язування задач логічного характеру з використанням кругів Ейлера
Навчально-методичний посібник
для вчителів та учнів
Кривий Ріг - 2018
Кривоносова Т. Р. Розв’язування задач логічного характеру з використанням кругів Ейлера:[Навчально-методичний посібник для вчителів та учнів] / М.В. Ткачук. – Кривий Ріг : КЦМГ, 2017. – с. 44
У посібнику зібрані і об’єднані за складністю задачі логічного змісту, які розв’язуються за допомогою діаграм Ейлера-Венна.
Посібник може бути використаний для організації позакласних занять, доповнення уроків математики нестандартними задачами, факультативних занять та підготовки учнів до математичних змагань і олімпіад.
Рецензенти:
Бас В.М. – вчитель математики, спеціаліст вищої категорії, старший вчитель КЦМГ
Навчально-методичний посібник друкується для участі у міському конкурсі «НА ШЛЯХУ ДО ВЕРШИН МАЙСТЕРНОСТІ»
З м і с т
РОЗДІЛ 1. ТЕОРЕТИЧНІ ВІДОМОСТІ ТЕОРІЇ МНОЖИ
1.1. Множина. Елементи множини
1.2. Підмножина. Операції над множинами
РОЗДІЛ 2. РОЗВ’ЯЗУВАННЯ ЛОГІЧНИХ ЗАДАЧ, ВИКОРИСТОВУЮЧИ ДІАГРАМИ ЕЙЛЕРА-ВЕННА
2.1. Розв’язування задач арифметичним способом
2.2. Розв’язування задач алгебраїчним способом
СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ
П е р е д м о в а
Навчально-методичний посібник розрахований для учнів та вчителів математики загальноосвітніх навчальних закладів.
Розв’язання будь-якої задачі тією чи іншою мірою базується на проведенні певних роздумів. Існують задачі, які можна розв’язати майже без обчислень. Для цього потрібно тільки послідовні (логічні) міркування, бажання, наполегливість, кмітливість і терпіння.
У шкільному курсі математики особливе місце посідають завдання логічного характеру. Такі задачі приваблюють учнів, своїм життєвим спрямуванням, нестандартним цікавим формулюванням умови, що сприяє формування у нас зацікавленості до предмету математики. Розв’язування задач такого змісту вчить аналізувати, порівнювати, робити висновки, а іноді й шукати нестандартні способи розв’язування. Такі вміння допоможуть учням у майбутньому не лише оволодіти математикою чи іншою наукою, а ще й в житті не ховатися від проблем (якщо розглядати їх як життєві задачі та шукати шляхи вирішення).
«Якщо ви власними силами розв’язали задачу, ви зробили відкриття. Якщо задача нескладна, то ваше відкриття не може претендувати на грандіозність; проте воно від цього не перестає бути відкриттям».
РОЗДІЛ 1. ТЕОРЕТИЧНІ ВІДОМОСТІ ТЕОРІЇ МНОЖИ
1.1. Множина. Елементи множини
Немає вченого, ім’я якого згадувалось би в навчальній математичній літературі так часто, як ім’я Ейлера. В 1741 році Ейлер пише «Письма о разных физических и философических материях, написанные к некоторой немецкой принцессе…», де вперше з’явились «Круги Ейлера». Ейлер писав тоді, що круги дуже підходять для того, щоб полегшити наші роздуми.
При розв’язуванні цілого ряду задач Леонард Ейлер використовував ідею зображення множин за допомогою кругів, які надалі і отримали назву «Круги Ейлера».
За допомогою цих кругів вчений зобразив співвідношення між множинами дійсних чисел, які вивчаються у шкільному курсі математики:
- N – множина натуральних чисел;
- Z – множина цілих чисел;
- Q – множина раціональних (дробових) чисел;
- R – множина дійсних чисел (всі числа числової вісі)
Співвідношення між цими множинами можна подати за допомогою рисунка 1.
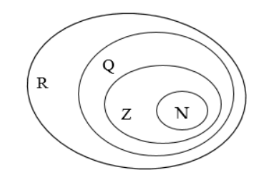
Рис.1.1.
Точного означення «множини» у математиці не існує. У математиці набір предметів або понять, зібраних за будь-якою ознакою, називають множинами, а кожний із цих предметів – елемент множини.
Поняття множина, подібно поняттям точки, числа, прямої і т.д., не зводиться до інших понять математики й, тому строго визначення немає. Можна сказати, що множина – це «сукупність», «набір», «ансамбль», «колекція», «клас» і т.д. Але все це не є математичним означеннями. Для того, щоб зрозуміти, що таке множина, наведемо приклади. Ми маємо право казати про множину всіх піщин у пісочних годинниках, про множену всіх квітів у вазі, про множину всіх зірок на небі, про всіх тварин на Землі, про множину атомів на Сонце й т.д. У звичайному житті, правда не кажуть множина корів, а скажуть просто череда, не множина коней – а табун, не множина учнів – клас. Дуже важливо завжди визначити ознаку, за якою об’єкти поєднуються в ту або іншу множину, який елемент буде входить до даної множини, кажуть «належати множині», а який – ні. Наприклад, розглянемо множину учнів 5-Б класу. Чи є елементом цієї множини дошка? Парта? Портфель? Конкретний учень? А чи є така множина, що містить всі перераховані елементи? Так, – це множина «класна кімната».
Множини можуть бути:
Скінченні (елементи якої можна перерахувати, наприклад – множина цифр 1,2,3,4,5,6,7,8,9,0 – 10 елементів );
Нескінченні (елементи якої перерахувати неможливо, наприклад – множина всіх натуральних чисел);
Порожні (множина, яка не містить жодного елемента, позначається Ø);
Злічені (множини, елементи якої можна перерахувати, іншими словами, кожному елементу присвоїти порядковий номер);
Незлічені (нескінченна множина, елементам якої не можна у відповідність поставити порядковий номер).
Позначають множини великими латинськими літерами (А, В, С, D, K, M,…). Наприклад, множина всіх цифр А={0, 1, 2, 3, 4, 5, 6, 7, 8, 9}. Елементи множини прийнято позначати малими латинськими літерами (a, b, c, d, k, m,…). Наприклад, а ![]()
![]()
![]() » позначає «не належить множині», наприклад, а
» позначає «не належить множині», наприклад, а![]() А. Читають: «елемент а не належить множині А».
А. Читають: «елемент а не належить множині А».
Завдання 1. Визначити який знак поставити «![]()
![]() » :
» :
Риба * множина тварин, що видають звуки;
Чорнило * множина напоїв;
Август * множина римських імператорів;
Дніпро * множина українських річок;
Математика * множина улюблених предметів.
Риба ![]() множина тварин, що видають звуки;
множина тварин, що видають звуки;
Завдання 2. Записати, які фігури належать множині А, а які – множині В; які фігури тільки множині А, тільки множині В?
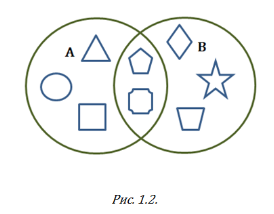
1.2. Підмножина. Операції над множинами
Ми знаємо, що предмети і явища навколишнього світу не існують незалежно один від одного, вони взаємозалежні одне від одного. Такі ж зв’язки існують і між множинами.
Кожен клас є частиною школи, родина є частиною роду, множина прямокутників є частиною множини всіх чотирикутників.
Тоді, якщо множина А={1,3,5,7,9,11,13,15}, а множина В={1,3,5,7}, то множина В є частиною множини А. Але, як сказав А. Пуанкаре: «Математика – спосіб називати різні речі одним ім’ям». І для цього в математиці є своя назва, тому множину В називають підмножиною множини А. Тобто, якщо кожний елемент множини В є також елементом множини А, то множина В називається підмножиною множини А. Позначається: В![]() А, в іншому випадку A
А, в іншому випадку A![]() B
B
Якщо є А={1,3,5,7,9,11} і В={2,4,6,8,10,}, то С={1,2,3,4,5,6,7,8,9,10,11,} – об’єднання множин А і В.
Об’єднанням (сумою) множин А і В називають таку множину С, яка містить у собі всі елементи множини А і ті елементи множини В, яких немає у множині А.
Позначають об’єднання значком «![]() ».
».
Тому С = А ![]() В або С = А + В.
В або С = А + В.
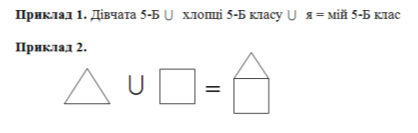
Це можна зобразити за допомогою діаграми Венна різними способами:
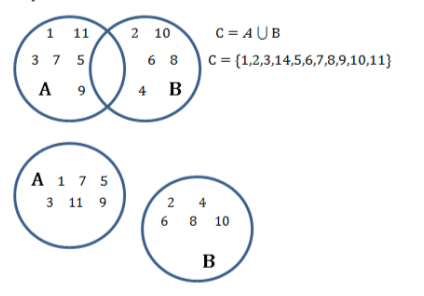
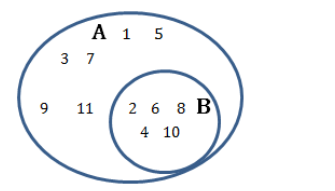
Рис. 1.3.
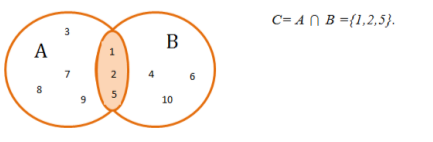
Розглянемо множину А={1,2,3,5,7,8,9} і множину В={1,2,4,5,6,10}. У них є однакові елементи або спільні елементи 1,2,5. Ці елементи складають множину С, яку називають перерізом множин А і В.
Перерізом (добутком) множин А і В називають така множина С, яка складається лише зі спільних елементів множин А і В.
Позначають переріз значком «![]() ».
».
Тобто С = А ![]() В або С = А . В.
В або С = А . В.
На діаграмах Ейлера-Венна це виглядає так:



3 5
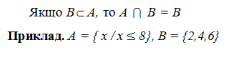 А 1 В
А 1 В
2 4
7 8 6
Рис. 1.4.
Різницею множини А і множини В, називається така множина С, яка містить всі елементи множини А, але не містить елементів множини В.
Позначається різниця значком « \ ». Тобто С = А \ В
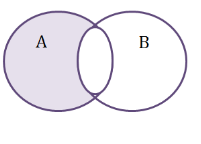 Діаграмою Ейлера-Венна це можна зобразити таким чином:
Діаграмою Ейлера-Венна це можна зобразити таким чином:
С = А \ В
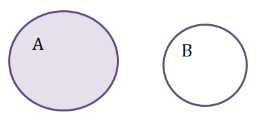
С = А \ В
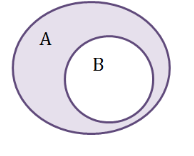
С = А \ В
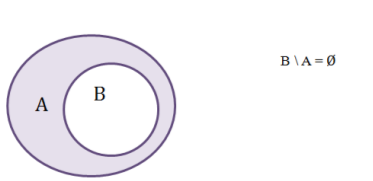
Рис. 1.5.
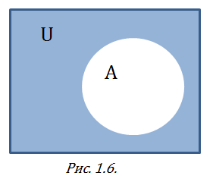
Для універсальної множини U, відносне доповнення деякої множини A до U називається абсолютним доповненням (або просто доповненням) A, і позначається як ![]() .
.
Позначається : ![]() = U \ A
= U \ A
Закони доповнення:
-
A ∪
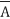 . = U
. = U
-
A ∩
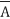 . = Ø
. = Ø
-
Ø
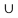
- U ∩ Ø = Ø
На діаграмі Венна це виглядає так:
Завдання для самостійного опрацювання
-



 Нехай маємо дві множини К={b ; ; ; 6 } і М = {9; b ; *; ; ; d ; 6 }.
Нехай маємо дві множини К={b ; ; ; 6 } і М = {9; b ; *; ; ; d ; 6 }.
- Яка із цих множин є підмножиною іншої?
- Задайте кругами Ейлера співвідношення множин К і М.
- На рис. 1.7. показано діаграму множин М і N. Розмістіть на цій діаграмі два елементи (у вигляді крапок) так, щоб: 1) вони належали обом множинам; 2) кожна з даних множин дістала по одному елементу; 3) у множині М будо два елементи, а у множині N – жодного.


![]()
![]()
Рис. 1.7.
- На рис. 1.8. множини А, В і С задані кругами Ейлера. Розмістити два елементи m і n так, щоб вказані множини мали відповідно: 1) по 2 елементи; 2) 2, 2 і 1 елемент; 3) 3, 1 і 0 елементів; 4) по 1 елементу.
- Розмістіть три елементи (рис. 1.8.) x, y, і z так, щоб множини А, В і С мали відповідно: 1) по 2 елементи; 2) по 1 елементу; 3) 1, 2 і 3 елементи; 4) 1, 3 і 3 елементи; 5) 0, 2 і 3 елементи.
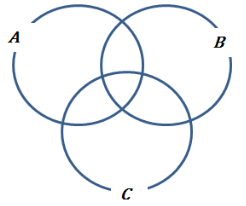
Рис. 1.8.
- Зобразіть рис. 1.9. у зошиті. Множинами А, В і С будемо вважати точки, що належать частинам аркуша, обмеженими відповідними діаграмами. Вкажіть кольором множину, яка складається з елементів: 1) лише множини А; 2) лише множини В; 3) лише множини С; 4) усіх трьох множин; 5) множини А і В, які не належать множині С; 6) множини В і С, які не належать А.
- Прочитайте казку Г. Остера «Пампукская хрюря». Намалюйте діаграму Венна і запишіть множину, про яку йде мова.
«Якось одного разу Слоненя, Удав і Мавпа сиділи й розмовляли. Раптом прилетів Папуга й запитав:
- Ви знаєте, що таке кукаляка?
- Ні, не знаємо,- відповіло Слоненя.
- Кукаляка, - важливо сказав Папуга, - це така
скринька, у якому лежить мукука.
- А що таке мукука?- запитала Мавпочка.
- Мукука - це така коробочка, у якій лежить бисяка,- відповів Папуга.
- А бисяка, що таке?- зачудувався Удав.
- Бисяка - це шухлядка, у якому лежить хрюря,- сказав Папуга. Подумав і додав: « Папукская хрюря».
- Що це за пампукская хрюря?- обурився Удав.- Ніяких пампукских хрюрей я ніколи не бачив!
-Пампукская хрюря - це такий пакетик, у якому лежить мамурик.
-Зрозуміло,- сказало Слоненя,- мамурик - це, напевно, теж яка-небудь шухлядка, у якому лежить ще що-небудь. Ну, а все-таки, що ж там у самій середині цих шухлядок, коробок і пакетиків? Скажи, будь ласка, Папуга.
- А хіба це так важливо? - відповів Папуга й полетів».
7. Запишіть всі підмножини таких множин:
1)С={m,n,f};
2)D={1,a,3,c,4,t};
3)S={1,2,3,4,5};
4) T={![]() }.
}.
8. Знайти переріз наступних множин:
1)A={a,b,c,d}, B={n,t,f,g};
2)A={2,4,6,7}, B={1,2,3,4};
3)A={a,b,c}, B={b,c,a};
4)A={1,a,3,c,5,t}, B={2,a,3,5,9}.
9. Знайти об'єднання наступних множин:
1)A={a,b,c,d,n}, B={a,n,d,t};
2)A={a,b,c}, B={1,2,3,4};
3)A={1,2,3,4,5,6}, B={2,4,6,7,8,9}.
10. Дано множини А і В, знайти об'єднання й переріз цих множин, якщо:
1) А - множина чисел кратних 5 і менших 100, В - множину чисел менших 105 і кратних 7;
2) А - множина чисел кратних 2 і менших 65, В - множину чисел менших 65 і кратних 3.
РОЗДІЛ 2. РОЗВ’ЯЗУВАННЯ ЛОГІЧНИХ ЗАДАЧ, ВИКОРИСТОВУЮЧИ ДІАГРАМИ ЕЙЛЕРА-ВЕННА
2.1. Розв’язування задач арифметичним способом
Відомий математик Леонард Ейлер (1707-1783) запропонував чудовий спосіб розв’язування задач, у яких потрібно знайти перетин чи об’єднання певних множин, – зобразити їх геометричною схемою. Такі схеми називають кругами Ейлера, або діаграми Ейлера-Венна, оскільки пізніше, в 1894 р., Дж.Венн запропонував аналогічну методику використання діаграм для розв’язування логічних задач.
Цей спосіб графічного зображення множин допомагає унаочнити відношення між множинами, що значно полегшує розв’язування задач.
Розглянемо приклади розв’язування логічних задач.
Задача 1
Відомо, що 15 учнів класу колекціонують марки, а 16 листівки, з них 6 – і марки, і листівки. Скільки учнів класу колекціонують лише марки?
Розв’язання: Позначимо множину учнів, які колекціонують марки, як М, а множину тих, хто колекціонує листівки, - як Л. Зобразимо відповідні множини у вигляді кругів Ейлера.


![]()
![]()
![]()
Рис. 2.1
Із графічної інтерпретації видно, що тільки марки колекціонують
15-6=9 учнів.
Відповідь: 9 учнів.
Задача 2
Серед 30 дітей було проведено опитування. Виявилося, що 12 з них полюбляють печиво, 14 – цукерки, а 6 – не люблять ні печиво, ні цукерки. Скільком любителям печива смакують цукерки?
Розв’язання:
Позначимо множину дітей, що полюбляють печиво, як П, а цукерки - як Ц, і подамо умову задачі за допомогою діаграми Ейлера-Венна.
- 30 – 6 = 24 (д.) – полюбляють печиво та цукерки всього;
- 24 – 14 = 10 (д.) – люблять печиво, але не люблять цукерок;
- 12 - 10 = 2 (д.) – люблять і печиво, і цукерки;
Відповідь: 2 дітям смакують і печиво, і цукерки.

![]()


![]()
![]()
![]()
Не люблять нічого – 6
Рис. 2.2.
Задача 3 (Кенгуру-2017)
У гурті 30 дівчаток. 18 з них пили сік, 16 пили каву, а деякі не пили нічого. Тих, хто пив і сік, і каву, у 2 рази більше, ніж тих, хто нічого не пив. Скільки дівчаток пили і сік, і каву?
Розв’язання: Зобразимо умову задачі графічно діаграмою Ейлера-Венна:
- 30 - 16 = 14 (д.) – ті,що пили сік без кави;
- 30 - 18 = 12 (д.) – ті, що пили каву без соку;
- 14 + 12 = 26 (д.) – ті, що пили сік і каву разом;
- 30 - 26 = 4 (д.) – ті,що нічого не пили нічого;
-
4

![]()



![]()
![]()
![]()
Не пили нічого
Рис. 2.3.
Відповідь: 8 дівчат пили і сік, і каву.
Задача 4
Всі мої друзі мають які-небудь смартфони. Шестеро із них мають iPhone, п’ятеро - Samsung. І тільки у двох із них є і iPhone, і Samsung. Угадайте, скільки у мене друзів?
Розв’язання:
- 6 – 2 = 4 (д.) – мають лише iPhone;
- 5 – 2 = 3 (д.) – мають лише Samsung;
- 4 + 3 + 2 = 9 (д.) – всього.
Відповідь: 9 друзів.


iPhone 2 Samsung
6 iPhone 5
Samsung
Рис. 2.4.
Задача 5
З 20 людей двоє вивчали лише англійську мову, троє – тільки німецьку, шестеро – тільки французьку. Троє не вивчали ніякі мови. Один вивчав англійську і німецьку, троє – англійську і французьку. Скільки людей вивчало німецьку і французьку мови?
Розв’язання: Зобразимо умову задачі графічно:
- 20 – 3 = 17 (л.) – вивчають англійську, німецьку і французьку разом;
- 2 + 3 + 1 = 6 (л.) – вивчають англійську;
- 17 – 6 =11 (л.) – вивчають французьку разом з німецькою, але не вивчають англійську;
- 11 – (3 + 6) = 2 (л.) - вивчають і французьку, і німецьку.
Відповідь: 2 людини.

![]()


![]()
![]()
![]()

![]()
![]()
![]()
Не вчать нічого - 3
Рис. 2.5.
Задача 6
У групі зі 100 туристів 66 володіють англійською мовою, 54 французькою і 33 людини володіють обома мовами. Скільки туристів у групі не знають ні англійської, ні французької мови?
Розв’язання:
Зобразимо за допомогою діаграми Ейлера-Венна. Позначимо А – туристи, які вивчають англійську, Ф - туристи, які вивчають французьку. Будемо шукати доповнення до множин А і Ф – туристи, які не знають ні англійської, ні французької мови (рис. 2.6.)
- 66 – 33 = 33 (т.) – знають англійську, але не знають французьку;
- 54 – 33 = 21 (т.) – знають французьку, але не знають англійську;
- 33 + 21 = 54 (т.) – лише англійську і лише французьку разом;
- 100 – (54 + 33) = 13 (т.) – не вивчають ні англійську, ні французьку.
![]() Відповідь: 13 туристів.
Відповідь: 13 туристів.

![]()


![]()
![]()
![]()
Рис. 2.6.
Задача 7
У ліцеї 70 учнів. З них 27 займаються в драмгуртку, 32 співають у хорі, 22 захоплюються спортом. У драмгуртку 10 учнів з хору, а у хорі 6 спортсменів, у драмгуртку 8 спортсменів. Три спортсмена відвідують і драмгурток, і хор. Скільки учнів не співають в хорі, не захоплюються спортом, і не займаються у драматичному гуртку?
Розв’язання:
Зобразимо усіх учнів за допомогою універсальної множини, а всередині розмістимо круги: Д – драмгурток, Х – хор, С – спорт (рис. 2.7).
- Спільні частини кругів:
Д і Х – учні, які займаються у драмгуртку і хорі; їх 10;
С і Х – спортсмени, які співають у хорі; їх 6;
С і Д – спортсмени, які займаються у драмгуртку; їх 8;
- Спільна частина всіх трьох кругів Д, Х і С – це учні, які займаються трьома заняттями, їх 3. Тому:
10 – 3 = 7 – учні, які займаються лише у драмгуртку і хорі;
6 – 3 = 3 – учні, які займаються лише спортом і співають у хорі;
8 – 3 = 5 – учні які займаються лише у драмгуртку і спортом;
- Тоді займаються:
- 27–(7 + 3 + 5) = 12 (у.) – займаються лише в драматичному театрі;
- 32 – (7 + 3 + 3) = 19 (у.) – відвідують лише хор;
- 22 –(5 + 3 + 3) = 11 (у.) – займаються лише спортом;
- 70 – (12 + 19 + 11+7 + 3 + 5 + 3) = 10 (у.) – не мають ніяких вподобань.
Відповідь: 10 учнів.

![]()
Не мають ніяких вподобань -?


![]()
![]()
![]()

![]()
![]()
![]()
![]()
Рис. 2.7.
Задача 8
У двох десятих класах школи навчається 50 учнів. З них 12 балів мають з алгебри мають 13 учнів, із фізики – 17 учнів, із хімії – 16. Лише з алгебри такі оцінки мають 5 учнів, із фізики – 3 учні, із хімії – 4 учні. Семеро дітей мають 12 балів із фізики й алгебри, із них четверо також із хімії.
- У скількох учнів 12 балів лише з алгебри і хімії?
- У скількох учнів 12 балів за два із трьох зазначених предметів?
- Скільки учнів не навчаються на 12 балів із жодного із цих предметів?
Розв’язання: Зобразимо діаграму Ейлера-Венна (рис. 2.8.)
- Знайдемо кількість учнів, які мають 12 балів лише з А і Х (?):
13- (5 + 3 + 4)=1 – учень
- Знайдемо кількість учнів, які мають 12 балів за два із трьох зазначених предметів: додамо всі перетини множин А, Х і Ф. Знайдемо тих учнів, які мають 12 балів лише з Ф і Х (?):
16 – 4 = 12 – лише з Ф, але не з Х;
17 – (3 + 4 + 3) = 7 – лише з Ф і Х;
- + 7 + 3 = 11 – лише по двом з трьох предметів.
- Знайдемо кількість учнів, які не навчаються на 12 балів із жодного із цих предметів?
50 – (13 + 4 + 7+ 3) = 23 або
50 – (16 + 3 + 3 + 5) = 23 або
50 – (17 + 5 + 1 + 4) = 23 або
50 – (5 + 1 + 3 + 4 + 7 + 4 +3) = 23
Відповідь: 1) 1 учень; 2) 11 учнів; 3) 23 учні .

![]()
Нічим не захоплюються - ?


![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
Рис. 2.8.
Задачі для самостійного опрацювання
- У групі дитячого садочка 18 дітлахів. Кожен із них виступав на святі новорічної ялинки: співали й танцювали. Семеро дітей співали.
- Скільки дітей танцювали, якщо п’ятеро і співали, і танцювали? (16 дітей)
- Скільки дітей виступило лише з таночком? (11 дітей)
- Із 30 учнів 10 класу лише троє не відвідують позакласні заняття. Проте 20 обрали спецкурс з математики, а 12 – з історії. Скільки учнів цього класу відвідують обидва спецкурси? (5 учнів)
- Серед мешканців Кракова 85% розмовляють польською мовою, 35% - українською, а частина вміє розмовляти обома мовами. Скільки %-ків жителів розмовляють обома мовами? (20%)
- Серед 24 учнів класу 8-А класу 16 подобається алгебра, 10 – геометрія, а п’ятеро – «не товаришують» з математикою. Скільком учням подобаються два предмети? (7 учнів)
- До Євро-2012 готували багато перекладачів. У групі зі 100 осіб 70 перекладатимуть з англійської, 60 – із французької, а 10 – не знають ні англійської, ні французької, вони перекладатимуть з японської. Скільки осіб може перекладати з двох мов? (40 осіб)
- * Підлога кімнати має площу 12 м2 застелена трьома килимами. Площа одного із них 5м2, другого 4м2, третього 3м2. Кожні два з них покривають спільну площу 1,5м2. До того ж площа 0,5м2 (з цих 1,5м2) закрита одночасно трьома килимами. Яку площу підлоги не закрито жодним із килимів? Яку площу закриває лише перший із килимів? (1. 4м2; 2. 2,5м2)
- * У класі 39 учнів. З них 16 грають у футбол, 12 – у баскетбол, 19 – у волейбол. Четверо грають і у футбол, і у волейбол, троє – у футбол і волейбол, четверо – у баскетбол і волейбол. Двоє займаються трьома видами спорту. Скільки учнів не займаються жодним видом спорту? Скільки учнів займається тільки баскетболом? (1. 3 учні; 2. 6 учнів)
- * У таборі відпочивають 70 дітей. З них 27 займаються у театральному гуртку, 32 – у конструкторському, 23 – у спортивному. У театральному гуртку 8 спортсменів і 9 конструкторів, серед конструкторів – 13 спортсменів. А от займатися у всіх трьох гуртках ніхто не встигає.
- Скільки дітей займаються лише спортом?
- Скільки дітей не відвідує жодного із цих гуртків? (1. 1 дитина ; 2. 19 дітей )
- * У деякій школі є клас захоплених хлопців. Сім учнів з цього класу захоплюються математикою, шість - фізикою, п’ять – астрономією. Четверо учнів захоплюються і математико, і фізикою, троє – математико і астрономією, двоє – фізикою і астрономією, а один – і математико, і фізико, і астрономією. Скільки учнів в цьому класі? (Не менше 10 учнів)
- * До шинку завітало 40 козаків, щоб поїсти вареники з вишнями, сливами і капустою. Виявилося, що двоє козаків їли вареники тільки з вишнями, четверо – тільки зі сливами, троє – тільки з капустою. Покуштували вареники із сливами та капустою, але не з вишням – семеро, із капустою і вишнями, але не зі сливами – п’ятеро, а 13 козаків поласували варениками трьох видів. Скільки козаків їли вареники лише з вишнями та сливами? (6 козаків)
2.2. Розв’язування задач алгебраїчним способом
Задача 1
На уроці алгебри учням було задано розв’язати рівняння, побудувати графік функції та довести нерівність. Із 24 учнів класу двоє правильно розв’язали лише рівняння, троє правильно довели лише нерівність, троє правильно виконали лише побудову графіка функції. Не розв’язали тільки рівняння – 4 учні, не довели тільки нерівність – 5 учнів, не побудували тільки графік – 2 учні. Решта дітей виконали всю роботу. Скільки таких дітей?
Розв’язання: Зобразимо діаграму Ейлера-Венна (рис. 2.9.) відповідно до умови задачі: відомо, що всього 24 учні, з них розв’язали лише рівняння (Р) – 2 (жовтий колір множини), лише графік (Г) – 5 (блакитний колір множини), лише нерівність (Н) – 3 (фіолетовий колір множини)
- Спільні частини кругів:
Р і Г – учні, які не довели тільки нерівність; їх 5;
Р і Н – учні, які не побудували тільки графік; їх 2;
Г і Н – учні, які не розв’язали тільки рівняння; їх 4;
- Спільна частина всіх трьох кругів Р, Г і Н – це решта учнів, які розв’язали всі три завдання, їх позначимо х.
Маємо рівняння:
х + 5 + 2 + 4 + 2 + 5 + 3 = 24;
х + 21 =24;
х = 3.
Відповідь: 3 учні

![]()


![]()
![]()
![]()

![]()
![]()
![]()
![]()
Рис. 2.9.
Задача 2
Із 30 учнів 20 користуються метро, 15 – автобусом, 23 – тролейбусом. Метро і тролейбус використовують 10 учнів. Метро і автобус – 12, а тролейбус і автобус – 9. Скільки учнів користуються трьома видами транспорту?
Розв’язання: Зобразимо умову задачі за допомогою рис. 2.10.
Позначимо учнів, які користуються трьома видами транспорту – х. Тоді позначимо:
(12 – х) – лише М і А;
(9 – х ) – лише Т і А;
(10 - х) – лише М і Т;
20 – (12 – х +10 – х + х) = 20 – 12 + х - 10 + х – х = х – 2 – лише М;
15 – (12 – х + 9 – х + х) = 15 – 12 + х – 9 + х – х = х – 6 – лише А;
23 – (10 – х + 9 – х + х) = 23 – 10 + х – 9 + х – х = х + 4 – лише Т;

![]()
![]()


![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
Рис. 2.10.
х – 2 + х – 6 + х + 4 + 12 – х + 9 – х + 10 – х + х = 30;
х + 27 = 30;
х = 3.
Відповідь: 3 учні .
Задача 3
У класі 38 учнів. З них 16 захоплюються математикою, 17 – фізикою, 18 – історією. Захоплюються тільки двома предметами – математикою і фізикою – четверо, математикою і історією – троє, фізикою і історією – п’ятеро. Троє не захоплюються ні математикою, ні фізико, ні історією.
- Скільки учнів одночасно захоплюються трьома предметами?
- Скільки всього учнів захоплюються лише одним із цих предметів?
Розв’язання: Зобразимо умову задачі за допомогою рис. 2.11.
Позначимо учнів, які захоплюються трьома предметами – у. Тоді згідно цього матимемо позначення.
- Кількість учнів, які захоплюються хоч чимось: 38 – 3 = 35;
- Захоплюються лише одним предметом:
16 – (3 + 4 + у) = 16 – 3 – 4 – у = 9 – у - лише М;
18 – (3 + 5 + у) = 18 – 3 – 5 – у = 10 – у - лише І;
17 – (4 + 5 + у) = 17 – 4 – 5 – у = 8 – у - лише Ф;
- Складемо відповідне рівняння:
9 - у + 10 - у + 8 - у + 4 + 5 + 3 + у = 35;
39 – 2у = 35;
2у = 4;
у = 2 – учні захоплюється трьома предметами
- Захоплюються лише одним предметом:
9 – 2 = 7 - лише М;
10 – 2 = 8 - лише І;
8 – 2 = 6 - лише Ф;
- 7 + 8 + 6 = 21 – всього учнів, які захоплюються лише одним із предметів.
Відповідь: 1) 2 учні ; 2) 21 учень .

![]()
![]()


![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
Рис. 2.11.
Задача №4
Із 32 хлопців у баскетбол грають 14 , у хокей – 22, у волейбол – 16. Баскетболом і хокеєм займаються 6 з них, баскетболом і волейболом – 4, волейболом і хокеєм – 5. Ніяким видом з цих видів спорту не займаються 3 з них.
- Скільки чоловік займаються трьома видами спорту одночасно?
- Скільки чоловік займаються лише в одній спортивній секції?
Розв’язання: Зобразимо умову задачі за допомогою рис. 2.12.
Позначимо хлопців, які займаються трьома видами спорту – х. Тоді згідно цього матимемо позначення.
- Кількість учнів, які захоплюються хоч чимось: 32 – 3 = 29;
- Захоплюються лише одним предметом:
14 – (6 + 4 + х) = 14 – 6 – 4 – х = 4 – х - лише Б;
20 – (6 + 5 + х) = 20 – 6 – 5 – х = 9 – х - лише Х;
16 – (4 + 5 + х) = 16 – 4 – 5 –х = 7 – х - лише В;
- Складемо відповідне рівняння:
4 - х + 9 - х + 7 - х + 4 + 5 + 6 + х = 29;
35 – 2х = 29;
2х = 35 – 29;
2х = 6;
х = 3 – учні захоплюється трьома предметами
- Захоплюються лише одним предметом:
4 – 3 = 1 - лише Б;
9 – 3 = 6 - лише Х;
7 – 3 = 4 - лише В;
- 1 + 4 + 6 = 11 – всього учнів, які захоплюються лише одним із предметів.
Відповідь: 1) 3 учні; 2) 11 учнів .

![]()


![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
Рис. 2.12
Задача 5
У 8 класі навчається 40 учнів. Кожний із них вивчає не менше однієї іноземної мови: англійську, німецьку, французьку. 34 учні вивчають хоча б одну із двох мов: англійську і німецьку. 25 учнів – хоча б одну із двох мов: німецьку і французьку. 6 учнів – тільки німецьку. Одночасно дві мови – англійську і німецьку – вивчають на 3 учні більше, ніж німецьку і французьку мови.
Скільки учнів вивчають кожну мову окремо і скільки вивчають одночасно кожні дві мови?
Розв’язання:
Зобразимо графічну схему (рис. 2.13) відповідно до умови задачі. Позначимо спільну множину Ф і Н – х, тоді спільну множину А і Н – (х+3).
Тільки А вивчають 34-(х+3)-6-х, а лише Ф –
25-(х+3)-6-х
Маємо рівняння:
34–(х + 3) –6 – х + х + 3 + 6 + х +25-(х + 3)-6 -х= 40;
34–х – 3 – 6 – х + х + 3 + 6 + х + 25 – х – 3 – 6 – х = 40;
34 + 25 – 3 – 6 – 40 = 2х;
2х = 10;
х=5.
![]()
![]()



![]()
![]()
![]()
![]()
![]()
![]()
Рис. 2.13.
Отже, тільки англійську вивчають 34 – (5 + 3) – 6 – 5 = 15 учнів, тільки французьку вивчають 25 – - (5 + 3) – 6 – 5 = 6 учнів; англійську і німецьку – 8 учнів; німецьку і французьку – 5.
Відповідь: 1) 8 учнів, 5 учнів; 2) 15 учнів, 6 учнів.
СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ
1. Апостолова Г.В. Логічними стежинками математики: 5-9-ті кл. / Г. В. Апостолова, О.П. Бакал. – 2-ге вид. – Київ: Генеза, 2016. С. 83-90
2. Басанько А.М., Романенко А.О. За лаштунками підручника з математики. – К.: Генеза, 2007. – 160 с.
3. Богомолова О. Б. Логические задачи. – М.: БИНОМ. Лаборатория знаний, 2006. – 271 с.
4. Гаврилова Т. Д. Занимательная математика. 5 - 11 классы. Волгоград: Учитель, 2005.-96 с.
5. Глейзер Г. И. История математики в школе — М.: Просвещение, 1964. — С. 232.
6. Савин А.С. Занимательные математические задачи. – М.: АСТ, 1995. – 138 с.
7. Титаренко О.М. 5770 задач з математики з відповідями. 2-ге вид. випр. – Харків: ТОРСІНГ ПЛЮС, 2007. – 336 с.
8. https://sibac.info/shcoolconf/science/xvii/42485
9. http://www.zaitsevairina.ru/html/f1143037846.html
10. http://mmmf.msu.ru/archive/20122013/z5/z5090313.html
11. http://www.kangaroo.com.ua/php_upload/data/pdf/5_class_UA17.pdf
Для нотаток
Для нотаток
1


про публікацію авторської розробки
Додати розробку

-

Пахомова Наталья Василівна
22.09.2023 в 12:42
Дякую!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Стецько Олександра Іванівна
05.03.2023 в 16:40
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Прошак Сергій Володимирович
22.09.2019 в 19:20
Щиро дякую.
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Пархоменко Олена Степанівна
24.02.2019 в 23:36
Загальна:
4.3
Структурованість
4.0
Оригінальність викладу
4.0
Відповідність темі
5.0
Показати ще 1 відгук