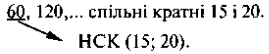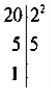Найменше спільне кратне кількох натуральних чисел
Урок № 6
Тема. Найменше спільне кратне кількох натуральних чисел
Мета: на основі знань про кратне число сформувати уявлення учнів про поняття спільного кратного кількох натуральних чисел, НСК, а також навчити їх користуватися алгоритмом знаходження НСК двох (трьох і т.д.) натуральних чисел.
Тип уроку: засвоєння нових знань.
Хід уроку
І. Перевірка домашнього завдання
Для більш цікавого протікання процесу перевірки домашнього завдання на уроці можна запропонувати учням провести цю роботу в ігровій формі, наприклад у вигляді гри «Знайди помилку». (Учитель заздалегідь записує на дошці розв'язання вправ домашньої роботи, припустившись кількох типових помилок. Учні, перевіряючи написане, повинні знайти помилку; можна організувати змагання: хто знайде більшу кількість помилок і зуміє їх пояснити.)
Для «слабких» учнів, домашнє завдання яких учитель перевіряє перед уроком, у цей час можна запропонувати роботу з картками-підказками.
|
Картка 1 Знайди НСД чисел 20 і 16. а) Розклади кожне з чисел на прості множники; |
|
|
|
|
|
б) Підкресли в розкладах цих чисел однакові прості множники, в) Знайди серед підкреслених однакових ті, що мають менший показник степеня, г) Знайди добуток цих степенів |
|
II. Актуалізація опорних знань
Запитання до класу
- Відомо, що а, b, с — натуральні числа і а = bс.
Як можна назвати число а по відношенню до b? по відношенню до а?
- Назвіть найменші три натуральних числа, кратних 2; 5; а.
III. Формування нових знань
Підходи до викладання теми НСК і НСД дуже схожі, тому цей етап уроку проводиться аналогічно до відповідного етапу попереднього уроку.
1. Постановка проблеми
Задача. До кіоску завезли зошити. Якщо розкласти по 15 зошитів або по 20 зошитів в пачку, то в обох випадках зайвих зошитів не залишиться. Яку (найменшу) кількість зошитів могли завезти до кіоску? Яка найменша кількість зошитів могла бути завезена?
Аналіз умови приводить до висновку, що під час розв'язування задачі треба знайти числа, які діляться (кратні) на 15 і на 20.
2. Розв'язання проблеми
Учні знайомляться з поняттями:
- спільне кратне кількох натуральних чисел, найменше спільне кратне (НСК);
-
алгоритм знаходження НСК кількох чисел.
Короткі нотатки можна оформити у вигляді такого конспекту:
|
Конспект 5 НСК 1. Числа, кратні 15: 15; 30; 45; 60; 75; 90; 105; 120;... Числа, кратні 20: 20; 40; 60; 80; 100; 120;...
|
||
|
а) |
|
б)15 = 3 · 5, 20 = 22 · 5;
в) НСК(15; 20) = 22 · 3 · 5 = 60. |
|
Зауваження. Спільні кратні |
||
Розв'язок задачі: НСК(15; 20) = 60, отже, найменша кількість зошитів 60; можливі варіанти 120, 180, 60п зошитів.
IV. Закріплення знань і формування вмінь
І рівень
Усні вправи
______________________________________
II рівень
Письмові вправи
- ______________________________________
-
Знайдіть найменше спільне кратне чисел:
а) 6 і 8; б) 72 і 99; в) 396 і 180; г) 34; 51 і 68. - У портовому місті починаються три туристичних рейси, перший з яких триває 15 діб, другий — 20, третій — 12 діб. Повернувшись до порту, теплоходи того ж дня вирушають у новий рейс. Сьогодні з порту вийшли теплоходи за всіма трьома маршрутами. Через скільки діб вони знову разом вийдуть у плавання?
- Число m кратне 12. Доведіть, що m ділиться на 4.
- Знайдіть найбільше двоцифрове число, кратне числам 2 і 7.
-
Знайдіть НСД чисел: а) 12 і 24; б) 75 і 45; в) 81 і 243. Чи є серед них
взаємно прості? - Виконайте дії: (1,87 + 1, 955) : 0,85 – (2 · 1,75 – 3,5) · 4,62.
V. Підсумок уроку
Підбиваючи підсумки, слід наголосити, що основний зміст теми «Подільність чисел» розглянуто і основні поняття і алгоритми можна знайти в конспектах 1—5, тому основна мета наступного уроку — доопрацювати теми НСД і НСК і показати розуміння вивченого матеріалу і вміння його застосовувати для розв'язування відповідних вправ.
VI. Домашнє завдання
_________________________________________
1


про публікацію авторської розробки
Додати розробку